声波强化传热的实验研究与机理分析
2021-03-05杨延锋姜根山许伟龙
杨延锋,姜根山,许伟龙,姜 羽
(1.华北电力大学 能源动力与机械工程学院,北京 102206;2.华北电力大学 数理学院,北京 102206)
声波诱导的周期性振荡流可以加强物质的扰动和掺混,并强化物质的传热能力[1-2]。因此,探究声波强化热、质传输的机理具有重要意义。
近年来,利用有源声学技术强化颗粒物的传热传质过程受到广泛关注[3-5],但目前的研究还停留在声波强化物质传热速率的参数化分析阶段,而对声波促进传热的内在机理认识不足。研究表明[6],简谐声波在传播过程中遇到障碍物时,将在障碍物外形成2种不同的流场,即与时间有关的振荡流和与时间无关且具有漩涡特性的稳定流(也称声流),这2种流场共同决定了障碍物外的流场特性和传热行为。声流主要存在于厚度为δv的黏性边界层中[7],通过动量和涡量的传递,边界层内声流可在边界层外诱导出尺度更大但强度较弱的外涡流[8]。Kotas等[9]通过粒子示踪(PIV)技术对球形颗粒外声流的流场结构进行了可视化研究。
探究声波对单颗粒传热的影响是理解复杂颗粒系统传热行为的重要依据。Sayegh等[10]对置于振荡流中单颗粒的传热行为进行数值分析,并给出努塞尔数的经验公式。Ha等[11-12]对球坐标系下二维非定常质量、动量和能量守恒方程进行了数值求解,研究了在有、无恒定流速的振荡流中颗粒的传热行为。Gopinath等[13]首次利用解析和数值求解技术对流雷诺数Res较大情况下声流运动引起的球体对流传热进行了研究。许伟龙等[14-16]计算出强声波作用下夹带在烟气中单颗粒煤粉的传热特性,并搭建了声波促进加热铜球冷却的实验平台,以进一步探究声波对传热效率的影响。
综上所述,虽然国内外对振荡流强化传热进行了大量研究,但大多只进行了特定频率范围内的实验研究或数值分析[17-18],缺乏宽频率范围内的传热研究。因此,笔者结合铜球黏性边界层内声流的产生机理,深度挖掘了声波强化铜球散热的物理机理,为有源声波技术在传热传质方面的工程应用提供参考。
1 理论分析
1.1 铜球对流传热
在球坐标系下,一维、非稳态、有内热源的铜球导热微分方程[19]为:
(1)
式中:ρcop为铜球的密度;cp,cop为铜球的比定压热容;λ为铜球的导热系数;r为距球心的距离;T为铜球温度;τ为铜球温度变化时间;Φ为铜球单位体积热源。
为封闭求解式(1),需结合相应的边界条件和初始条件。
(2)
T(r,0)=T0
(3)
式中:T(R,τ)为τ时刻铜球表面的温度;T(r,0)为初始时刻铜球内部任意点的温度;Tf为环境温度;T0为铜球的初始温度;Qs为声波传递给铜球的热量;hc为铜球表面与环境的对流传热系数;hr为辐射传热系数。
实验中铜球加热温度低于200 ℃,根据斯忒藩-玻耳兹曼定律可知,铜球的热辐射换热量可忽略。因此,式(2)可简化为:
(4)
在上述边界条件下,铜球内部温度分布受到毕渥数Bi的影响。
(5)
式中:δ为固体的特征尺度。
当Bi≪1时,可认为任意时刻固体内温度随时间均匀变化,与维度无关。因此,可采用集中参数法对式(1)进行简化。
(6)
根据能量守恒定律,铜球散失的热量应等于对流传热带走的热量。因此,可将铜球界面上交换的热量折算为整个物体的体积热源:
-ΦV=Ahc[T(τ)-Tf]
(7)
式中:V为铜球体积;A为铜球表面积;T(τ)为任意时刻铜球的温度。
因此,结合式(3)、式(6)和式(7),可得在声波影响下铜球传热的温度变化公式。
(8)
即:
(9)
式(9)符合二元一次线性方程形式,因此根据测得的实验数据可得到相应的曲线斜率,进而求得各工况下的对流传热系数hc。
声波对铜球与空气对流传热的影响程度可通过努塞尔数Nuc来表征,即:
(10)
式中:k为流体的导热系数;d为铜球的直径。
同时,努塞尔数Nuc可表征铜球表面热黏性边界层的导热热阻与对流热阻之比。相比铜球自然对流散热过程,声波对铜球散热的相对强弱影响可通过相对努塞尔数Nur来衡量,即:
Nur=Nuc/Nu0=hc/h0
(11)
式中:Nu0为铜球自然对流散热过程中的努塞尔数;h0为自然对流传热系数。
1.2 声流强化传热理论
针对球坐标系下不可压缩Navier-Stokes方程、连续性方程和能量方程,消除其压力项p后,引入相应的流函数Ψ,可得到简谐声波诱导振荡流在铜球外的无量纲流函数和能量微分方程[20]。
(12)

(13)
式中:τ1为声波作用时间;μ=cosθ,其中θ为周向角度;φ为无量纲温度;ε为声波引起的介质位移振幅与铜球直径之比;Pr为普朗特数;M为铜球直径与声波在铜球外形成的黏性边界层厚度之比,即M=d/δv。
当ε≫1时满足大振幅波动特性,声波与铜球发生强非线性相互作用,黏性边界层内的声流将发生流动分离;当ε≪1时满足小振幅波动特性,声波与铜球发生弱非线性相互作用,使声流保持层流状态,只有当ε≪1时才能简化式(12),得出相应的解析解。M表征简谐声波的黏性耗散效应在物体表面的扩散程度。M较小时,铜球外可形成较厚的黏性边界层,这时边界层内将形成强度较大的声流运动;M较大时,铜球外法线方向的流体经过黏性边界层后速度快速增大,最终到达振荡流区域,这时铜球的传热主要受边界层外振荡流的影响。
理论推导表明,在满足小振幅条件下,式(12)的解析解包含声流和振荡流2部分,即表示为以下形式:
Ψ=Ψs+Ψueiωτ1
(14)
式中:Ψs为声流流函数;Ψu为振荡流流函数;ω为声波角频率。
将式(14)代入式(12)和式(13)中,可得到小振幅条件下声流的流函数和能量微分方程。
(15)

(16)
通过流雷诺数可以描述声流的强弱和流场特性。当Res≪1时,声流对传热的影响很小,即振荡流是影响铜球传热行为的主要因素;当Res≫1时,铜球外存在范围广、强度大的声流运动,声流是强化传热过程的主要因素;当Res约等于1时,铜球的传热行为受到边界层内声流和边界层外振荡流的共同影响。由于式(15)和式(16)的耦合性质,一旦由式(15)确定了流场,即可根据式(16)确定给定普朗特数Pr下的温度分布。
流努塞尔数Nus与流雷诺数Res的关联式[13]为:
(17)
式中:A0、m和n均为常数。
流雷诺数Res与铜球的几何尺寸无关,完全由声波和传播介质的特性决定。
声压级SPL为:
(18)
式中:pe为有效声压;pref为参考声压,pref=2×10-5Pa;U0为介质速度振幅;Uref为参考速度,Uref=4.83×10-8m/s。
根据流雷诺数Res的定义,式(18)可改写为:
SPL=10×lg(ω0Res)
(19)
式中:ω0为无量纲声波角频率。
由式(19)可知,流雷诺数与声压级呈正相关,即声流强度随声压级的增大而增强。
联立式(17)和式(19),可推导出:
(20)
由式(20)可知,流努塞尔数Nus与声压级成正比,与无量纲声波角频率成反比,因此低频高强度声波作用于物体时,声流是影响传热行为的主要因素。
2 实验系统
图1给出了声波强化铜球散热的实验台架示意图。实验系统由温度测量系统、声测量系统和实验台架3部分组成。将K型热电偶插入铜球上0.5 mm的小孔中,由温度记录仪每隔1 s记录铜球的温度,采集60 s内铜球的温度变化。声测量系统由声发生装置和声接收装置组成。由声谱仪产生声信号,经功率放大器后扬声器产生稳定的正弦波信号。将声级计放置于铜球附近,以采集铜球所受声压级。实验台架设计成上下左右可调节的支架结构。每组实验先设定声频率和声压级,然后将铜球加热到(120±3) ℃,并置于扬声器喇叭口平面以上20 cm处,该距离处声压级几乎衰减至0 dB,因此可认为声波直接作用在铜球上。经测定,环境温度为27 ℃。作为对照组,实验中测定了铜球在无声波作用下的自然对流散热过程。实验中,铜球的直径d分别为5 mm、10 mm和15 mm;声压级分别为0 dB 、110 dB、120 dB和133 dB;声频率范围为500~3 000 Hz,其中在500~<1 500 Hz范围内步长为100 Hz,在1 500~3 000 Hz范围内步长为500 Hz。

图1 实验台架示意图Fig.1 Schematic diagram of the test bench
各工况条件均满足:声波波长远大于铜球直径(λ≫d);声波引起的振荡流为小振幅波动(ε≪1)。此外,实验在墙壁敷设有吸声海绵的封闭空间中进行,避免了自然风和反射波对传热的影响。以上实验环境使铜球仅受行波的直接作用,且在铜球表面热黏性边界层内可形成稳定的声流结构。
表1给出了铜球和空气的主要物性参数。
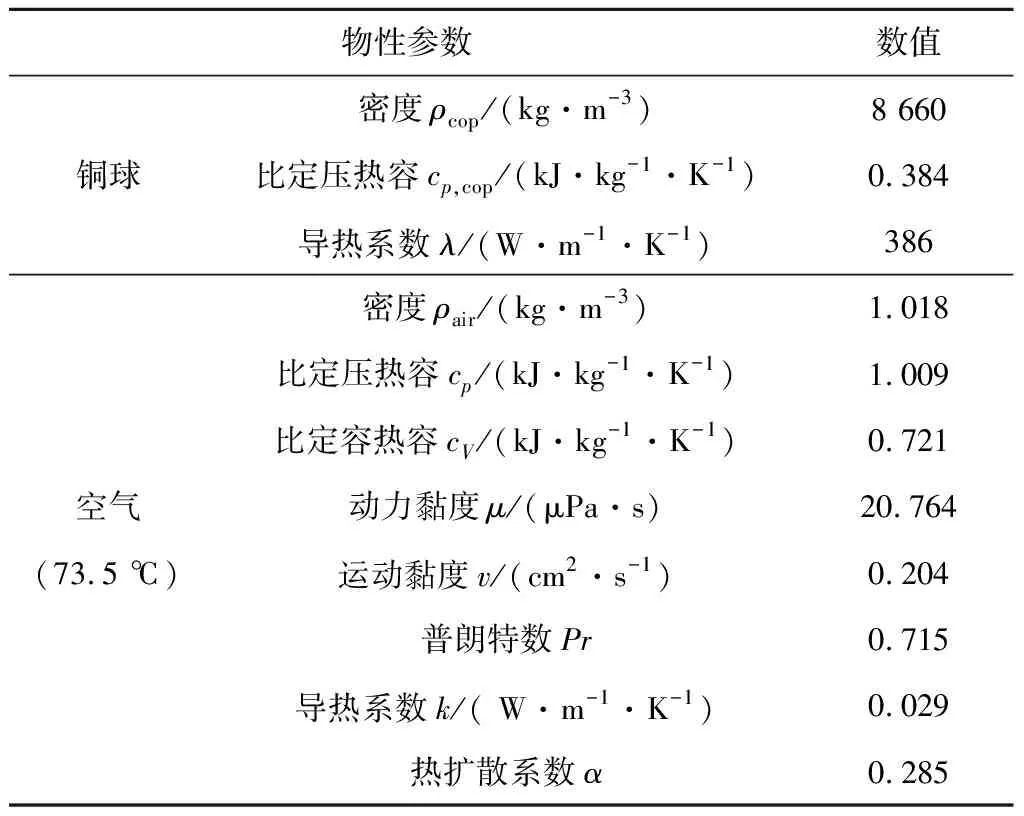
表1 物性参数
3 实验结果与讨论
3.1 铜球的对数无量纲温度
图2给出了声频率f为1 000 Hz、不同声压级下的对数无量纲温度。由图2可知,铜球对数无量纲温度随时间τ呈线性变化,且声压级越大,温度下降越快,表明一定强度的声波能强化铜球的散热过程。结合图2(a)~图2(c)可知,铜球直径越小,温度下降越快。这是因为铜球直径越小,将铜球加热到相同温度所吸收的热量越少,因此在相同时间内,小直径铜球的温度下降更快。
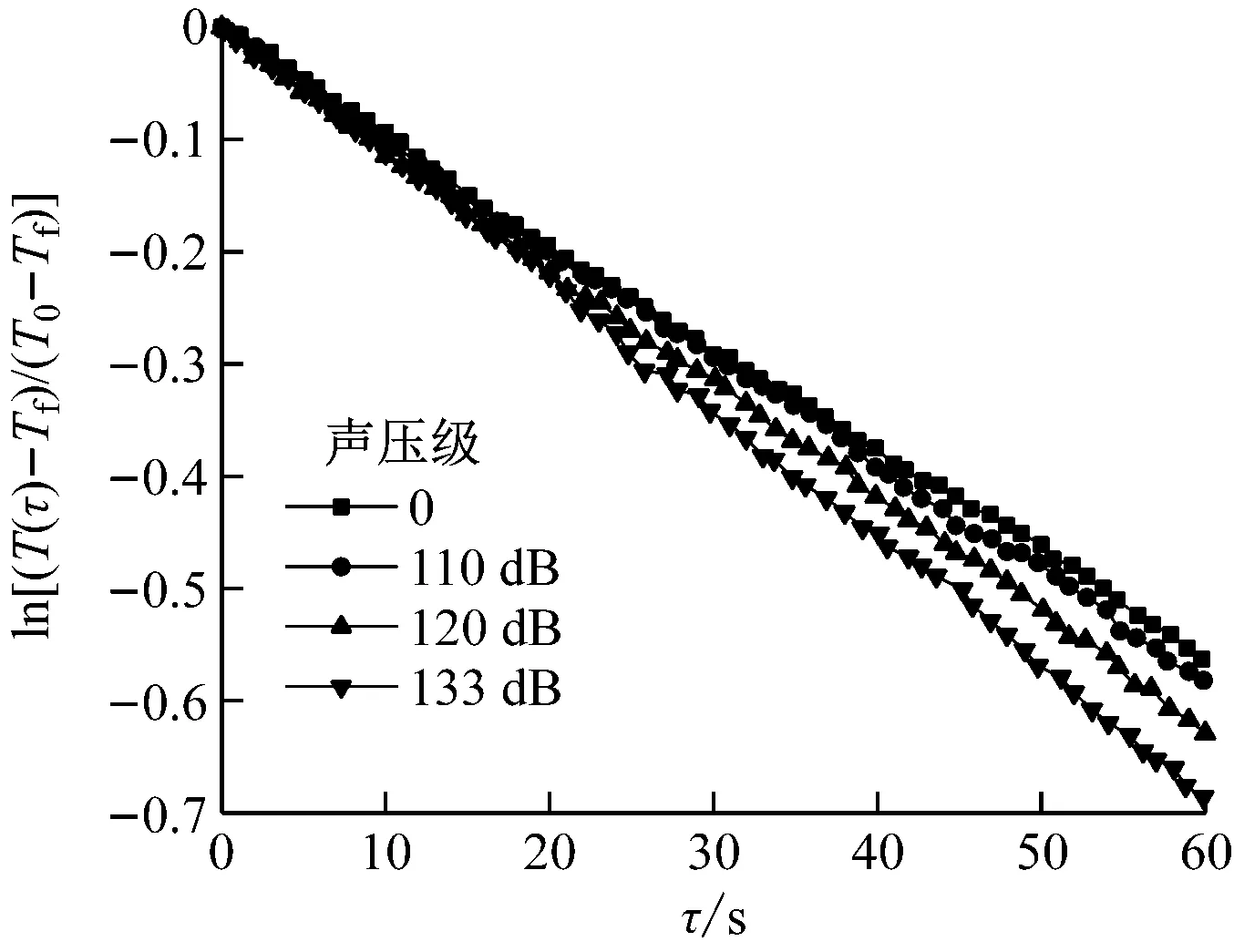
(a) d=5 mm

(b) d=10 mm

(c) d=15 mm图2 铜球对数无量纲温度的变化曲线Fig.2 Change curve of ln[(T(τ)-Tf)/(T0-Tf)] with τ
图3给出了声频率f为1 000 Hz、不同声压级下铜球(d=5 mm)的散热量和终温。由图3可知,随着声压级的增大,铜球散热量呈非线性增大趋势,而铜球的终温降低。这表明声压级大的声波能显著强化对流传热过程。
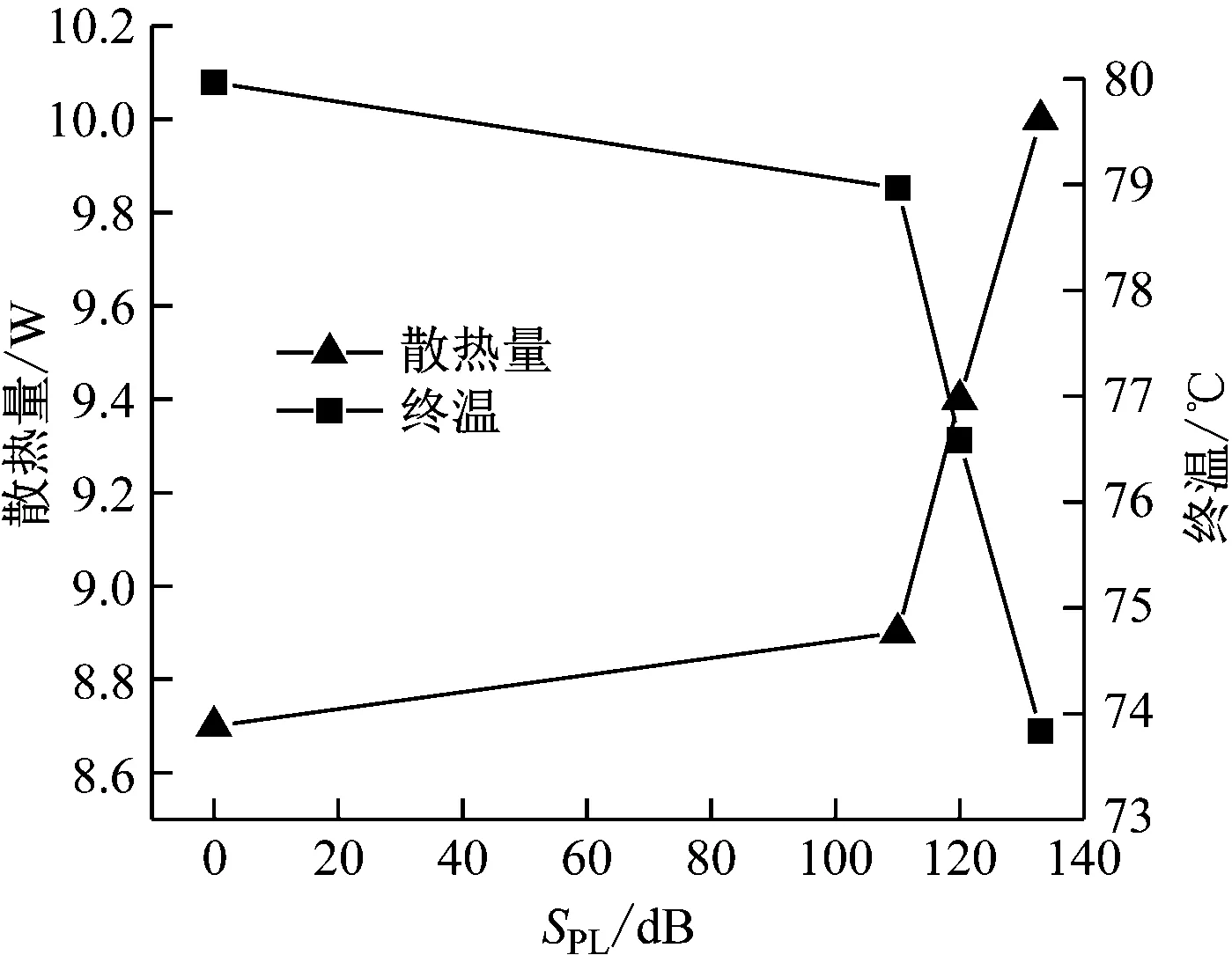
图3 铜球散热量和终温随声压级的变化Fig.3 Changes of heat dissipation and final temperature ofcopper sphere with sound pressure level
3.2 铜球对流传热系数
对图2中各工况下的离散点进行线性拟合,可得到各曲线的斜率,根据式(9)计算得到相应的对流传热系数hc。图4给出了不同直径铜球对流传热系数随声压级的变化趋势。由图4可知,不同直径下传热系数随声压级的增大而整体增大,声压级为133 dB时直径为5 mm铜球的对流传热系数最大;声压级相同时,铜球直径越小,对流传热系数越大。

图4 声压级对对流传热系数的影响Fig.4 Influence of sound pressure level on hc
计算可知,声压级SPL为110 dB、120 dB和133 dB时介质速度振幅U0分别为0.021 m/s、0.069 m/s和0.310 m/s。由此可见,133 dB声压级下的介质速度振幅是110 dB声压级下的14倍多,因此声压级为110~133 dB时对流传热系数明显增大;而声压级为0~110 dB时对流传热系数增幅较小,即该声压级范围内声波诱导的振荡流强度较弱。
3.3 努塞尔数Nuc
图5给出了不同工况下Nuc随声频率的变化。由图5可知,相比铜球的自然对流散热,在声波作用下铜球的对流传热过程得到强化;存在最佳声频率,可使Nuc最大,这与系统共振有关[21],且最佳声频率随声压级的增大而提高。随着声频率的提高,不同直径铜球的Nuc变化规律不同。如图5(a)所示,铜球直径为5 mm时,随着声频率的提高,Nuc呈先减小后增大再减小的趋势,最后趋于稳定。由图5(b)和图5(c)可知,铜球直径为10 mm和15 mm时,随着声频率的提高,Nuc先增大后减小,最后趋于稳定。由图5可知,在不同声压级下Nuc达到峰值对应的声频率不同。这是因为声频率一方面直接影响声流的强弱和扰动范围,另一方面也会影响振荡流在球表面发生流动分离而生成漩涡的速率。此外,结合图5(a)~图5(c)可以看出,铜球直径越大,Nuc越大。给定声频率时,Nuc随着声压级的增大而增大,说明增大声压级是加速铜球散热的有效手段。
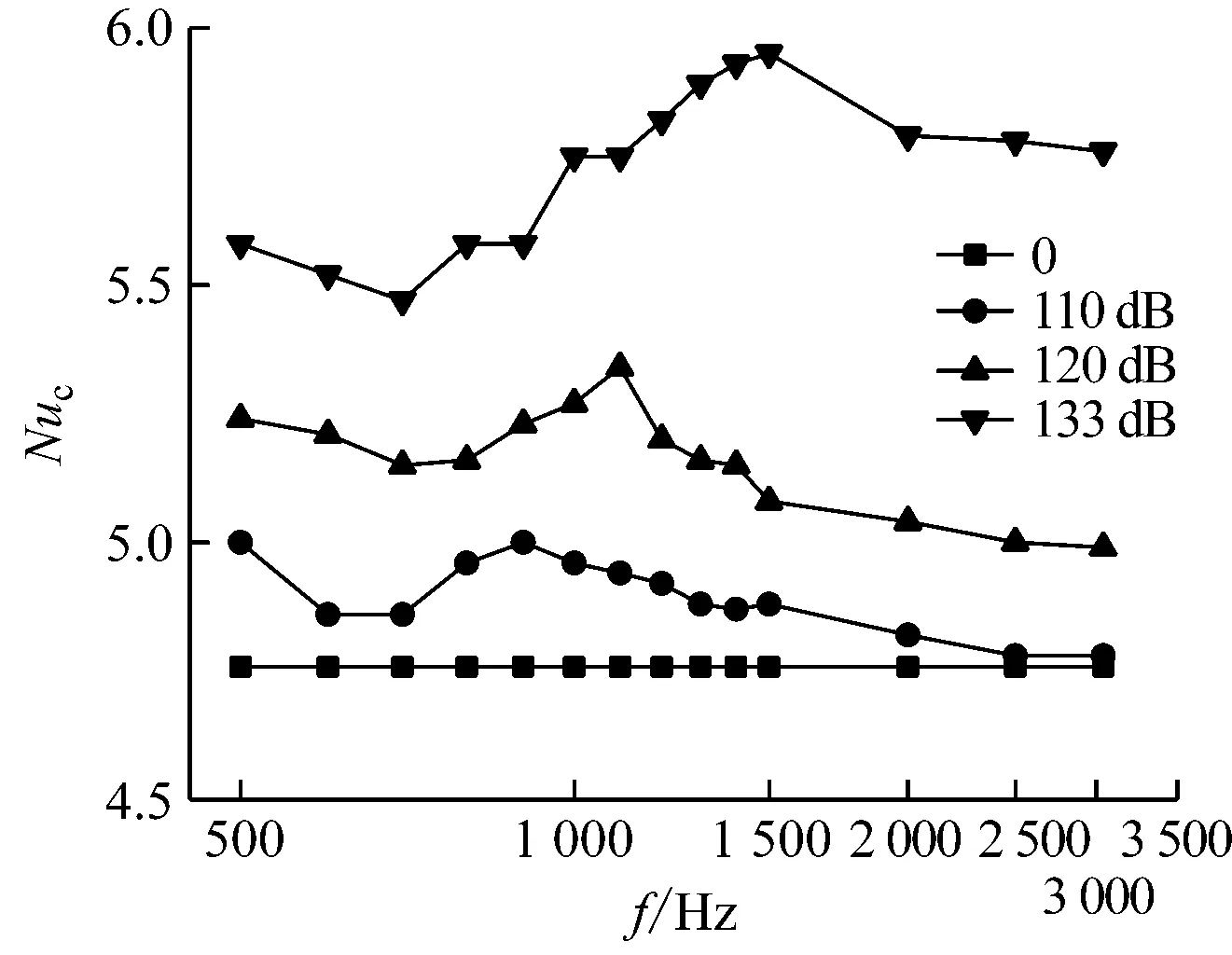
(a) d=5 mm

(b) d=10 mm
整合图5中不同直径铜球的数据,图6给出了相对努塞尔数Nur随声频率的变化曲线。由图6可知,不同直径的铜球在相同声压级下,Nur随声频率的变化规律基本一致。这表明与铜球自然对流散热相比,声波对不同直径铜球对流传热的强化能力相当。同时,图6也进一步说明声压级越大,声波强化铜球对流传热的能力越强。
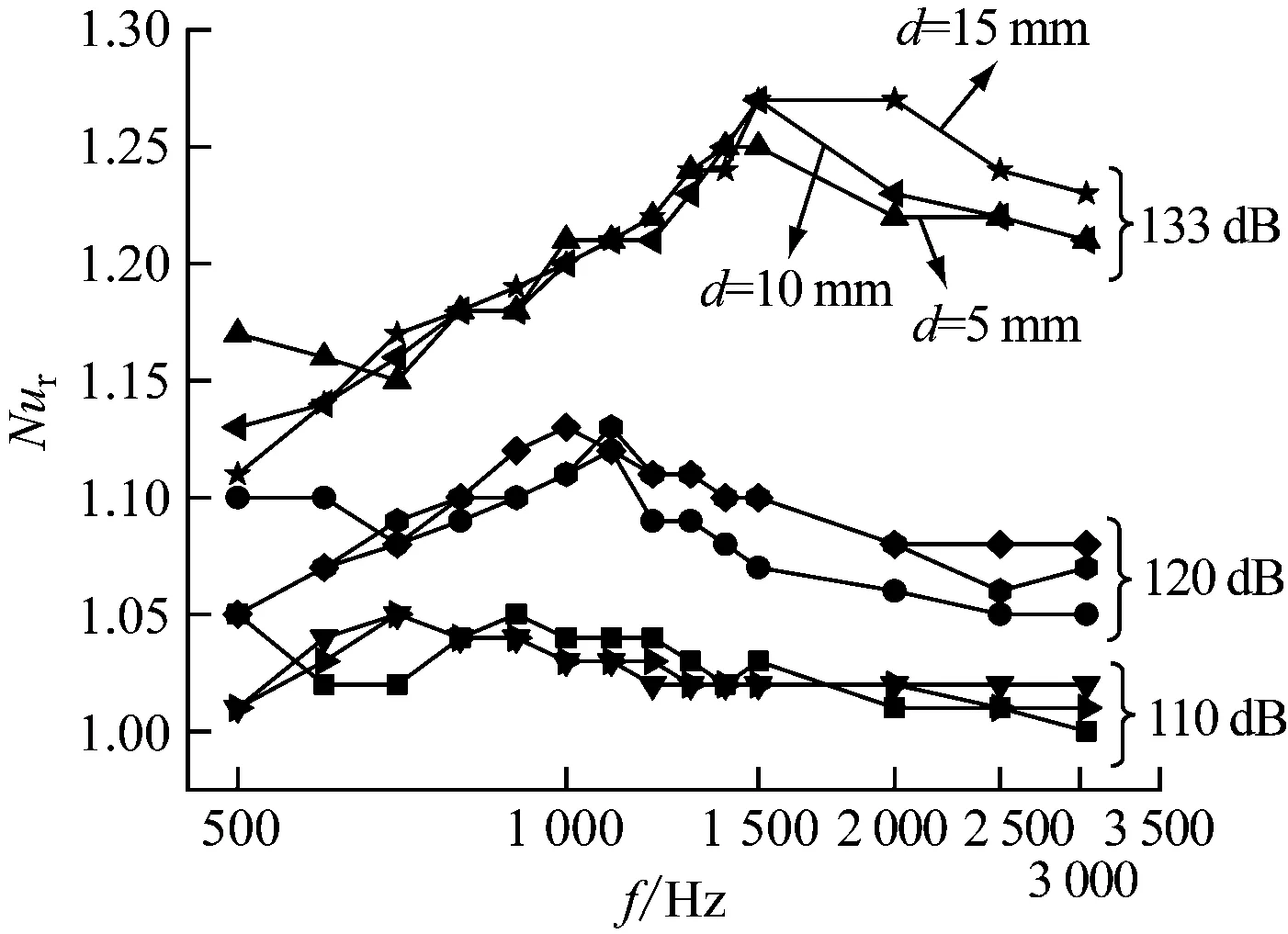
图6 相对努塞尔数Nur随声频率的变化规律Fig.6 Variation of Nur with acoustic frequency
3.4 声波强化铜球传热的机理分析
分析图5(a)~图5(c)中声压级为133 dB时的努塞尔数Nuc曲线可知,在相同声压级下不同直径铜球的Nuc变化趋势有所不同。根据声波在铜球壁面附近的相对黏性耗散尺度定义(即L=δv/d),δv表征了黏性边界层内的声流尺度大小。由此可知,声波在铜球表面的相对黏性耗散尺度随铜球直径和声波角频率的增大而减小,这表明大直径铜球外形成的声流运动范围相对较小,而小直径铜球外可形成扰动范围较大的声流运动。因此,相较于振荡流,小范围的声流运动对铜球传热的影响几乎可以忽略。以上分析说明,在相同声参数的声波作用下,大直径铜球传热行为主要由振荡流控制,而小直径铜球传热行为还受声流的影响。声波在铜球表面黏性边界层中形成的声流运动能持续扰动黏性边界层并使边界层厚度减小,这是声波加速热、质传输的重要机理。
为分析声频率对铜球各阶段传热行为的影响机理,图7给出了直径d为5 mm的铜球在133 dB声压级作用下努塞尔数Nuc、流雷诺数Res和黏性边界层厚度δv随声频率的变化曲线。

图7 声频率对努塞尔数Nuc的影响Fig.7 Influence of acoustic frequency on Nusselt number
由图7可知,对于给定的声压级,声频率对Nuc的影响可分为4个阶段。第1阶段为声流控制区(<700 Hz)。该阶段声流是影响热、质传输的主要因素,声频率低于700 Hz时声波可在铜球表面形成较厚的黏性边界层,层内强烈的声流运动是加速铜球散热的主要原因,声频率越低,声流作用越强。第1阶段内流雷诺数Res>1,即在该阶段声波强化铜球的散热过程中声流的影响要大于振荡流,且Nuc、Res和δv均随声频率的提高而减小,这也说明低频区声流运动是影响铜球传热的主要原因[2,18]。第2阶段为声流和振荡流协同控制区 (700~1 500 Hz)。该阶段黏性边界层内的声流运动仍起到一定作用,但随着声频率的提高,声流的影响逐渐减弱,而边界层外振荡流的影响逐渐增强。这是因为随着声频率的提高,振荡流引起的流动分离现象增强,形成较多的漩涡[22],而漩涡的脱落能及时带走铜球的热量,因此在第2阶段Nuc随着声频率的提高而增大。第3阶段为振荡流控制区(<1 500~2 000 Hz)。该阶段声流的影响存在于极薄的黏性边界层内,但其扰动强度受到极大抑制,可忽略不计。相反,随着声频率的进一步提高,铜球表面漩涡脱落的速度加快,使前1个即将脱落的漩涡还来不及对铜球表面进行冷却就被下1个生成的漩涡带走,导致Nuc随着声频率的提高而减小。第4阶段为稳定区(>2 000 Hz)。该阶段声波强化铜球传热的声振系统已达到稳定状态,流动分离产生的漩涡速率不再随声频率的变化而改变,该阶段流雷诺数Res≪1,且δv≪1,即声流的影响极小,因此该阶段严格来说也属于振荡流控制区。
3.5 声波强化铜球对流传热的经验公式
由图6可知,相对努塞尔数Nur受到声频率f和声压级SPL的综合影响,与铜球直径的关系不大。因此,以直径d=5 mm的铜球为例,针对图7中前3个阶段,采用麦夸特法并利用相应阶段的实验数据构建了对流传热经验公式。
第1阶段:
(21)
第2阶段:
(22)
第3阶段:
(23)
式(21)~式(23)的拟合相关系数分别为0.96、0.92和0.97,图8给出了其预测结果与实验结果的对比。由图8 可知,采用式(21)~式(23)得到的预测结果可靠性较高。
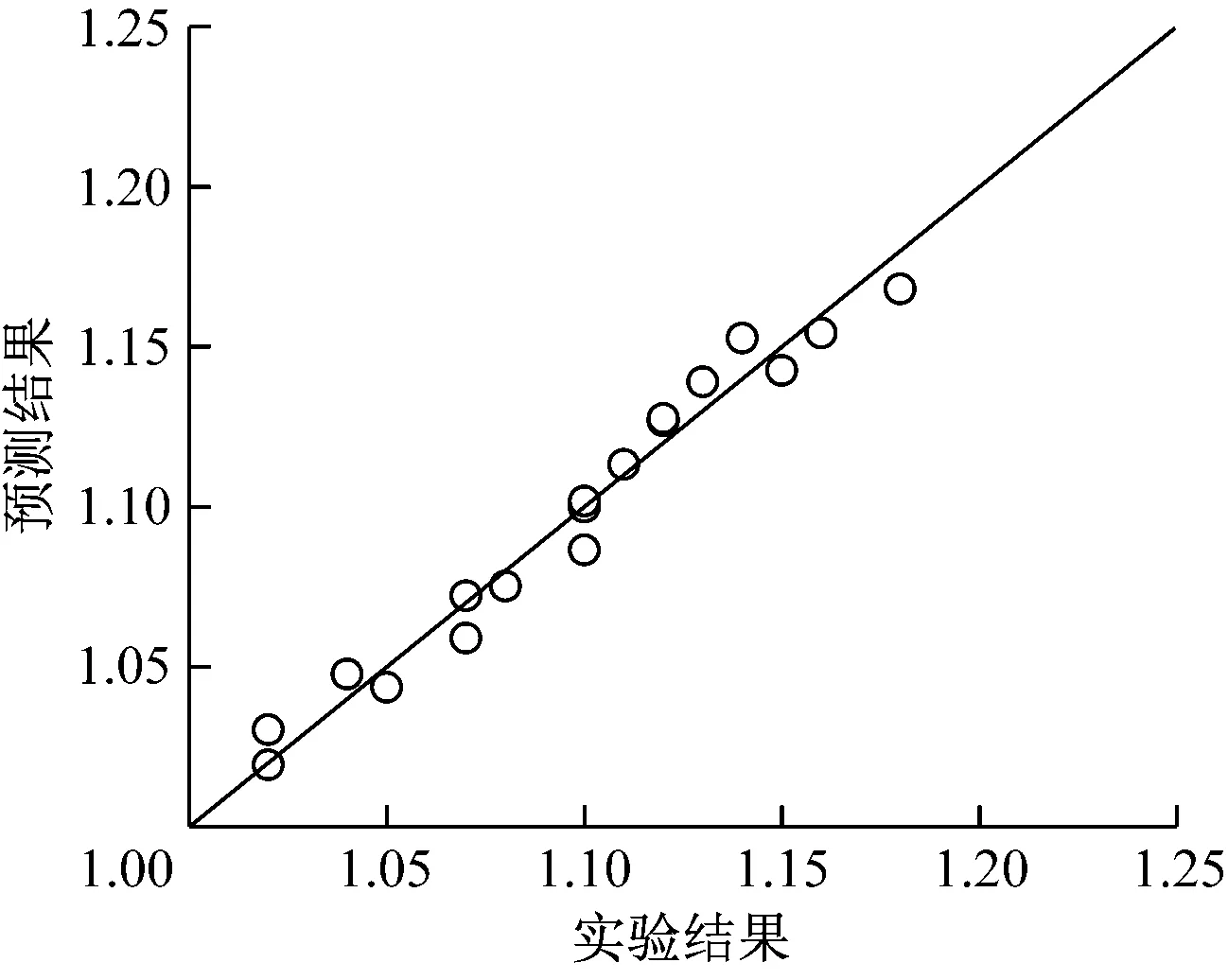
(a) 式(21)的预测结果

(b) 式(22)的预测结果
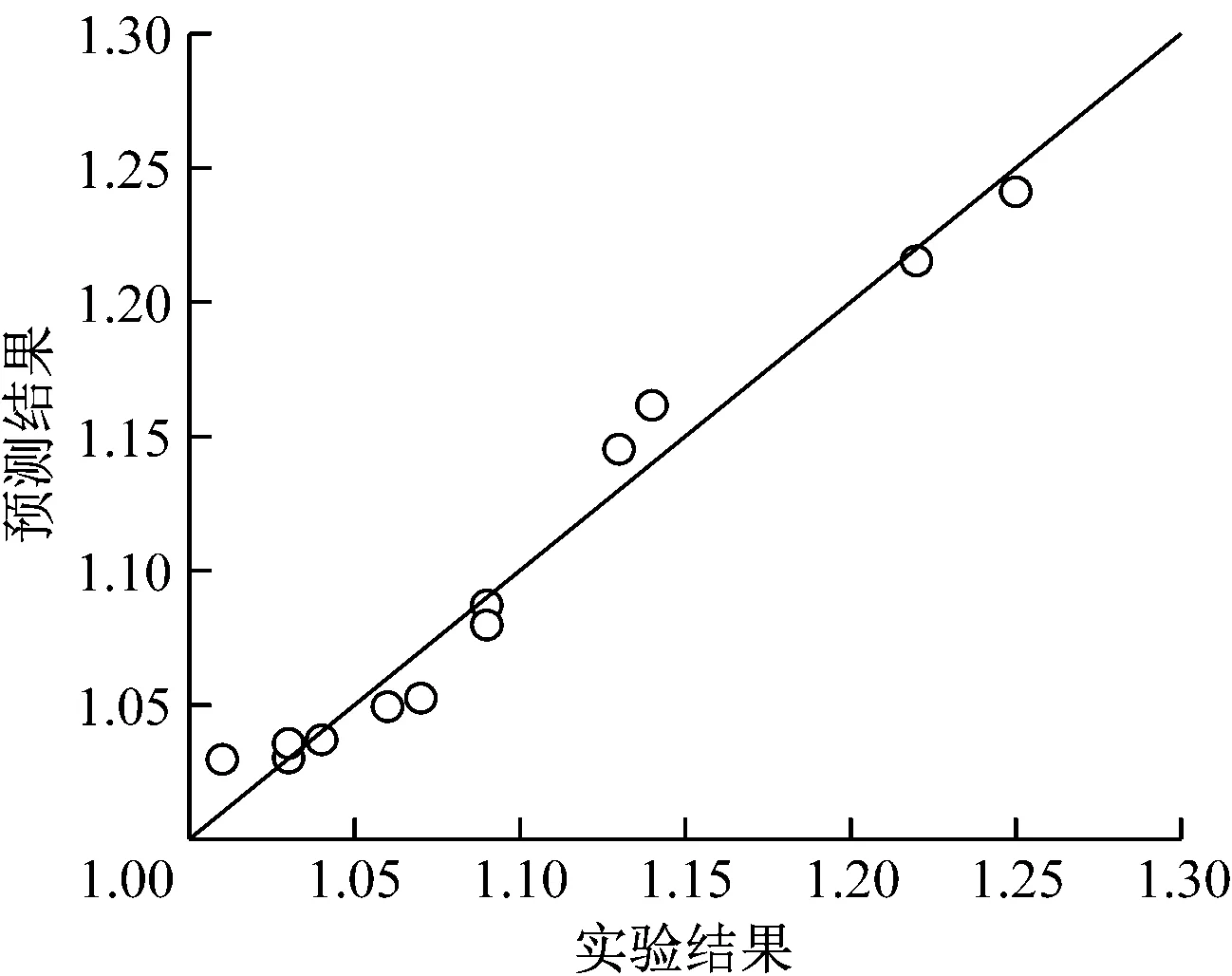
(c) 式(23)的预测结果图8 相对努塞尔数Nur预测结果与实验结果的对比Fig.8 Comparison of Nur between predicted values andexperimental results
4 结 论
(1) 铜球对流传热系数和努塞尔数受到声频率、声压级和物体特征尺度等参数的综合影响,而增大声压级是强化物体对流传热最直接有效的手段。
(2) 声波对物体传热的影响大致可分为4个阶段,即声流控制区、声流和振荡流协同控制区、振荡流控制区和稳定区。
(3) 存在最佳声频率,可使声波强化传热能力达到最强,且最佳声频率随着声压级的增大而提高。
(4) 相对努塞尔数受到声频率和声压级的综合影响,而与铜球直径的关系不大。
