基于LQG/LTR方法的小型堆功率控制器设计
2021-03-05李待兴张益林
石 波,李待兴,郭 伟,张益林
(中广核研究院有限公司, 广东深圳 518000)
小型堆由于具有用途广泛、建设周期短和安全性高等优点,逐渐成为国内外的研究热点[1]。但是,该堆型运行工况比大型堆更复杂,需要控制系统具备快速的负荷跟踪能力和良好的抗干扰能力。堆芯系统是保证压水堆安全稳定运行的重要组成部分,采用经典控制理论很难实现堆芯功率的良好控制[2]。
廖龙涛等[3]采用加权多模型设计了堆芯内模鲁棒控制器。王俊玲等[4]利用点堆方程设计了自适应保性能堆芯控制器。Rojas-Ramírez等[5]利用自适应控制理论计算模糊隶属度函数,设计了自适应模糊堆芯控制器。Gong等[6]基于H∞输出反馈控制理论设计了压水堆功率鲁棒控制器。Dong[7]根据非线性堆芯模型提出了自适应跟踪控制方法。Li等[8]采用T-S模糊模型设计了反应堆模糊鲁棒控制器。Kruger 等[9]基于反馈控制理论设计了功率鲁棒控制器。
相比上述鲁棒控制,笔者采用带有回路传输恢复(LTR)的线性二次型高斯(LQG)控制,即LQG/LTR方法。该方法具有良好的鲁棒性和解耦能力,同时对噪声具有良好的抑制能力,可利用最小的控制能量获得较小的控制误差。LQG/LTR方法在航空航天等多个领域得到广泛应用。在反应堆控制方面,该方法也用于大型堆的控制研究[10-12],而小型堆的系统结构和动态特性与大型堆差别较大,有必要进一步探讨LQG/LTR方法在该堆型功率控制中的应用。笔者根据物理和热工动力学原理建立了小型堆堆芯系统非线性仿真模型,并推导得到双输入双输出的状态空间模型。在此模型基础上,根据LQG/LTR方法的控制原理,开展小型堆堆芯系统的设计和仿真验证。
1 堆芯系统建模
1.1 数学模型
堆芯系统数学模型由点堆动力学方程、热工水力守恒方程以及反应性方程组成。基于单组缓发中子的点堆动力学方程[13]为:
(1)
式中:n为中子密度,m-3;ρ为总反应性;β为有效缓发中子的数量占比;Ci为单组缓发中子先驱核密度,m-3;t为时间;Λ为中子代时间,s;λ为缓发中子衰变常数,s-1;
对式(1)进行归一化处理,令:
(2)
式中:nr为相对中子密度,%;Cr为单组缓发中子先驱核的相对密度,%;n100为额定功率下的中子密度,m-3;C100为额定功率下缓发中子先驱核的密度,m-3。
将式(2)代入式(1),得到归一化的点堆中子动力学方程为:
(3)
只考虑慢化剂温度和燃料温度的负反馈效应,忽略氙、碘等毒物引入的反应性反馈,则反应堆总反应性方程为:
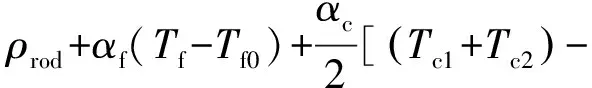
(Tc10+Tc20)]
(4)
式中:ρrod为控制棒引入的反应性;αf和αc分别为燃料温度和冷却剂温度反应性系数,K-1;Tf、Tc1、Tc2分别为燃料温度、冷却剂平均温度和冷却剂出口温度,℃;Tf0、Tc10和Tc20分别为初始燃料温度、初始冷却剂平均温度和初始冷却剂出口温度,℃。
热工水力模型采用平均通道等效近似来处理,冷却剂各节点的能量守恒方程以出口参数为集总参数,则燃料节点、2个冷却剂节点的能量守恒方程为:
(5)
式中:P0为反应堆满功率,W;μf和μc分别为燃料和冷却剂总热容量,J/K;f为燃料产生热量占总功率的比例;K为燃料与冷却剂间的传热系数,W/K;qm,p为冷却剂质量流量,kg/s;cp,c为冷却剂比定压热容,J/( kg·K);Tin为冷却剂入口温度,℃。
1.2 堆芯系统模型线性化
利用微小摄动的线性化理论,选取堆芯系统状态变量x=[δnrδCrδTfδTc1δTc2]T;输入变量u=[δρrodδTin]T;输出变量y=[δnrδTc2]T。其中,δ为微小扰动量。
将式(3)~式(5)在100%FP(满负荷)工况点 进行线性化处理,得到堆芯系统状态空间方程为:
(6)
其中,
式中:nr0为稳态相对中子密度。
将状态空间方程转化成传递函数形式,得到的双输入双输出传递函数矩阵为:
(7)
式中:Gr,11、Gr,12、Gr,21和Gr,22均为堆芯传递函数。
2 堆芯系统LQG/LTR控制器设计
2.1 LQG/LTR控制原理
图1为LQG/LTR控制系统框图。其中,r(t)为输入变量;u(t)为控制器输出变量;y(t)为输出变量;ζ(t)和θ(t)分别为扰动信号和噪声信号;Kc和Kf分别为状态空间反馈矩阵和Kalman滤波矩阵;G(s)为对象传递函数矩阵;Gc为控制器传递函数矩阵,对于单变量系统,其为标量形式;1/s为积分环节。
假设噪声信号θ(t)和扰动信号ζ(t)均为零均值的白噪声,其协方差矩阵Ξ=E[ζ(t)ζ(t)T]≥0,Θ=E[θ(t)θ(t)T]≥0。其中,Ξ为ζ(t)的协方差矩阵;Θ为θ(t)的协方差矩阵。
定义控制系统最优化性能指标J为:
(8)
式中:Q为对称矩阵,Q=QT≥0;R为对称正定矩阵,R=RT≥0,对于单变量系统,其为标量形式。
控制器传递函数矩阵Gc可表示为:
Gc=Kc(sI-A+BKc+KfC)-1Kf
(9)
Kc=R-1BTPc
(10)
Kf=PfCTΘ-1
(11)
式中:Pc和Pf均为正定矩阵;I为单位矩阵。
ATPc+PcA-PcBR-1BTPc+Q=0
(12)
PfAT+APf-PcCTΘ-1CPf+ΓΞΓT=0
(13)
式中:Γ为可调参量矩阵。
采用对象输入端回路传输恢复的设计方法时,控制器设计可分为2个步骤[11]:设计LQR控制器,通过选取适合的加权矩阵Q和R,使开环传递函数-Kc(sI-A)-1B的性能指标达到设计要求; 引入LTR技术,使系统开环传递函数尽可能接近直接采用状态反馈时的结果。即假设Γ=B、Ξ=Ξ0+qI,其中Ξ0为初始协方差矩阵,选择合适的虚拟噪声系数q,使补偿系统的传递函数接近目标回路的开环传递函数,实现回路传输恢复。
2.2 堆芯系统设计
以NuScale小型堆堆芯系统为研究对象,设计堆芯功率控制器,其主要参数见表1。假设堆芯控制棒棒位与反应性成正比,暂不考虑死区和磁滞回环,因此控制棒驱动机构可以采用积分环节表示。此外,为确保系统的零稳态误差,可以通过在被控对象与控制器之间增加积分器来实现。LQG/LTR堆芯系统如图2所示。

表1 堆芯系统的主要参数
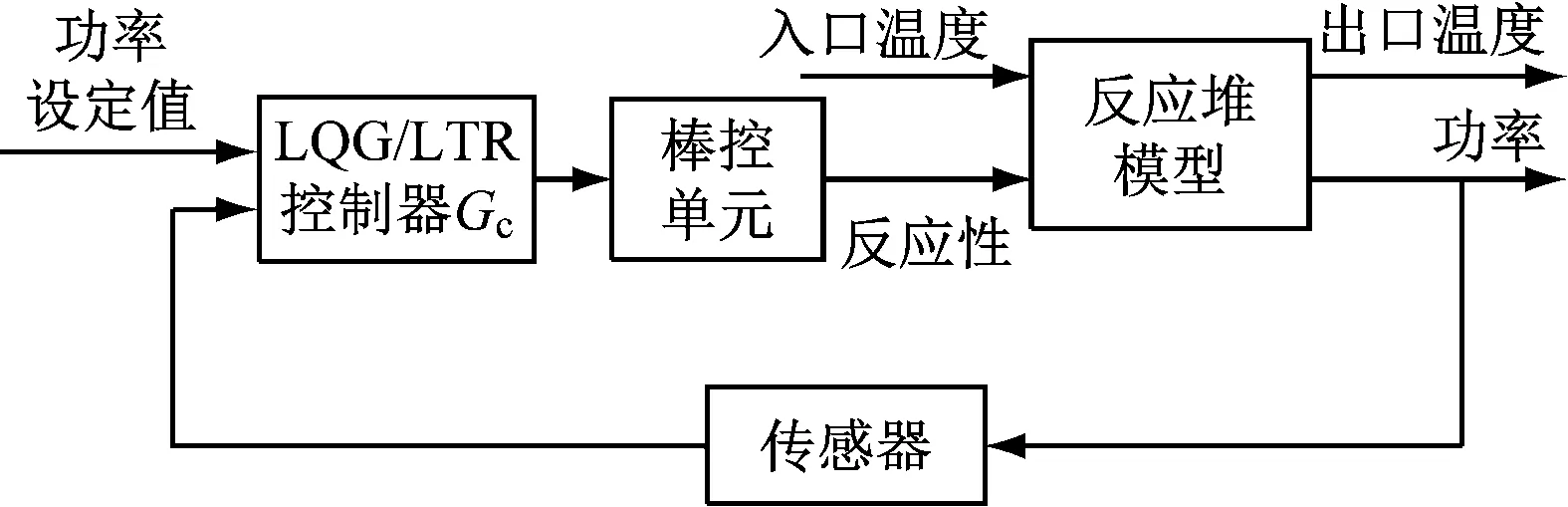
图2 LQG/LTR堆芯系统结构图Fig.2 Structural diagram of the core power control systembased on LQG/LTR method
通过选择合适的加权矩阵Q以及R值,使目标回路的开环传递函数-Kc(sI-A)-1B的性能达到满意的效果。假设当加权矩阵Q=CTC,目标回路奇异值曲线如图3所示。由图3可知,随着R值增大,目标回路在低频段的幅值和穿越频率不断减小,导致系统稳定性和动态响应性能下降。当R大于0.09时其变化对系统的影响较小。而在实际调节过程中,为尽量减少棒组的动作频率,应使目标回路中的权重尽可能大,即R尽可能大。综上,取R为0.09,得到状态空间反馈矩阵为Kc=10-7×[0.04 351 -0.02 -0.001 2.1×10-42.8×105]。
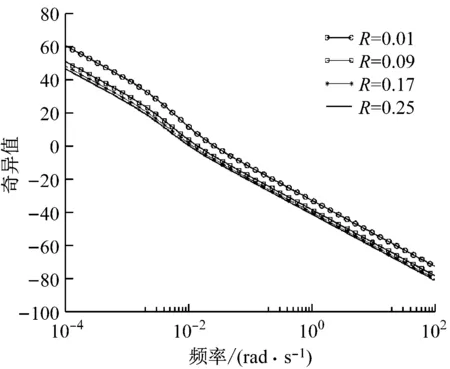
图3 目标回路的奇异值曲线Fig.3 Singular value curves of the target loop
对虚拟噪声系数q进行选择。随着q增大,开环系统的Nyquist曲线越接近目标回路的Nyquist曲线。但在实际应用中,q不应过大,否则会产生截断误差,并破坏系统的鲁棒性[10],因此取q=1010,此时开环系统Nyquist曲线与目标回路的Nyquist曲线几乎重合,如图4所示。

图4 开环系统和目标回路的Nyquist曲线Fig.4 Nyquist curves of the open-loop system and the target loop
最后,利用Matlab鲁棒系统设计工具箱计算得到LQG/LTR控制器传递函数Gc为:
(14)
加入控制器后整个开环系统的Bode图见图5,系统的幅值裕度为76.9 dB,相角裕度为69°,说明该系统具有较好的动态性能。

(a) 幅值
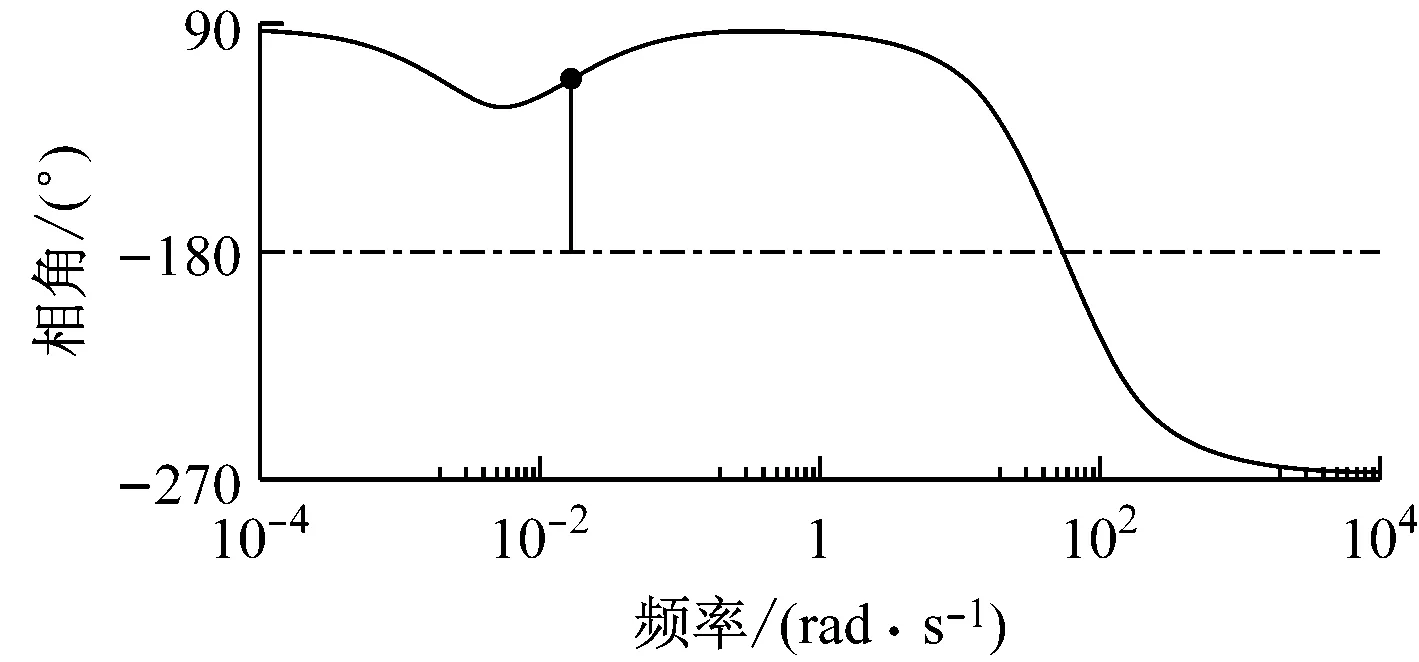
(B) 相角图5 开环系统的Bode图Fig.5 Bode plots of the open-loop system
3 堆芯系统仿真验证
在100%FP下,基于堆芯入口温度和功率参考值阶跃2种瞬态工况,将LQG/LTR控制与PID控制的性能进行对比。其中,PID控制采用单闭环结构,利用Matlab软件中的PID tuner工具计算得到最优化比例增益和积分时间。
3.1 堆芯入口温度阶跃
堆芯系统达到稳定后,在50 s时堆芯入口温度阶跃下降1 K,堆芯功率变化情况见图6。在初始阶段,由于冷却剂温度的负反馈作用,导致堆芯反应性增加,功率快速提高。此后,由于控制系统的作用,功率恢复到目标值。由图6可知,2种控制器均具有一定的抗干扰能力。但是,与PID控制相比,LQG/LTR控制具有更短的调节时间和更小的超调量,分别为20 s和0.05%。
由于控制棒动作导致的反应性变化曲线如图7所示。由图7可知,控制系统作用导致控制棒下插,引入的反应性最大为-35×10-5,100 s后堆芯系统达到平衡,由于控制棒动作引起的反应性变化为-25×10-5。
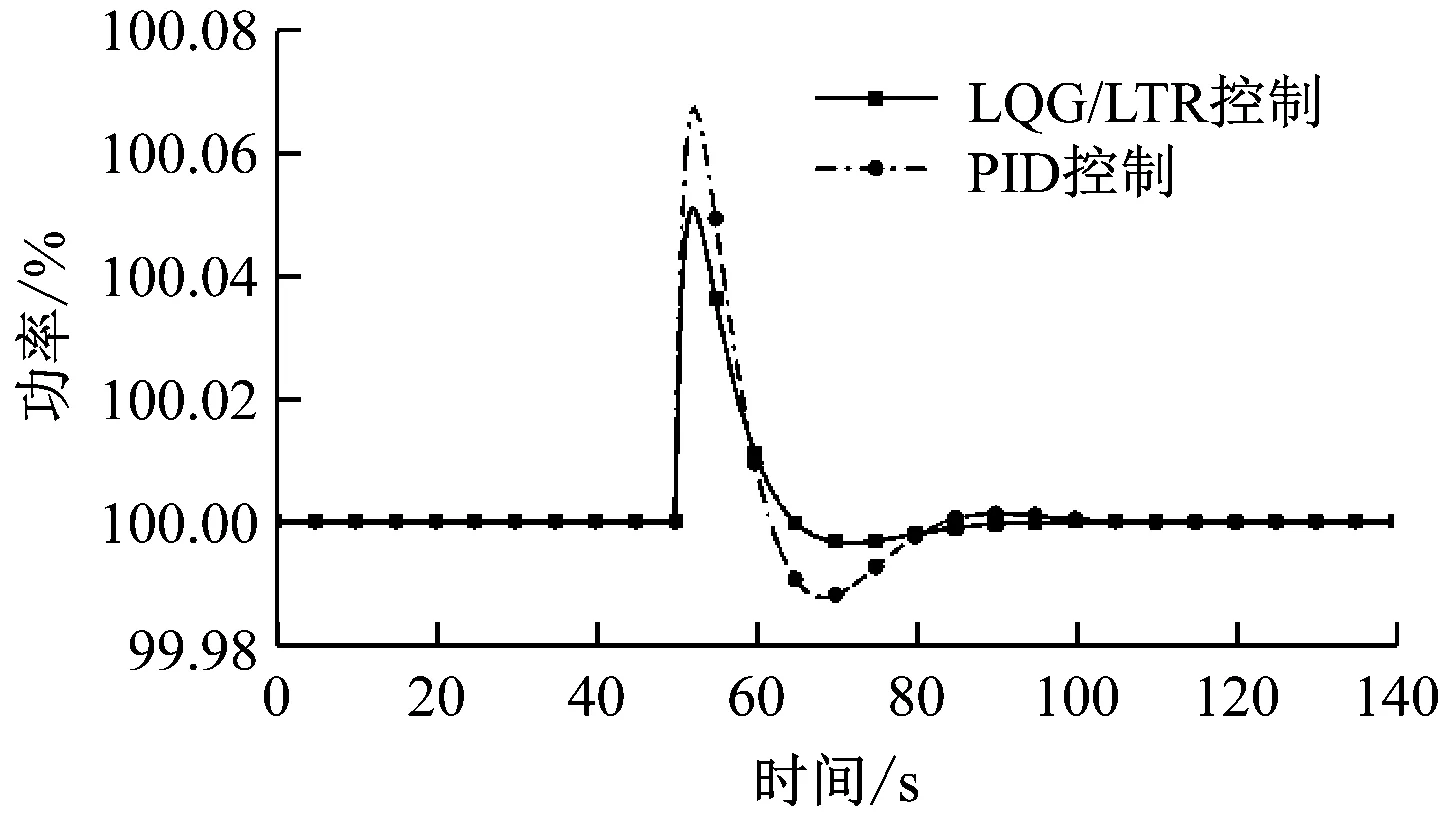
图6 入口温度阶跃时的功率变化Fig.6 Variation of power in response to a step change ofinlet temperature

图7 入口温度阶跃时的反应性变化Fig.7 Variation of reactivity in response to a step change ofinlet temperature
3.2 功率参考值阶跃
堆芯系统达到稳定后,在50 s时功率参考值阶跃提高10%,功率的变化趋势见图8。由图8可以看出,采用LQG/LTR控制器时系统稳定时间短于10 s,稳态误差为0%,超调量小于0.1%;而PID控制的稳定时间约为30 s,超调量大于1%。
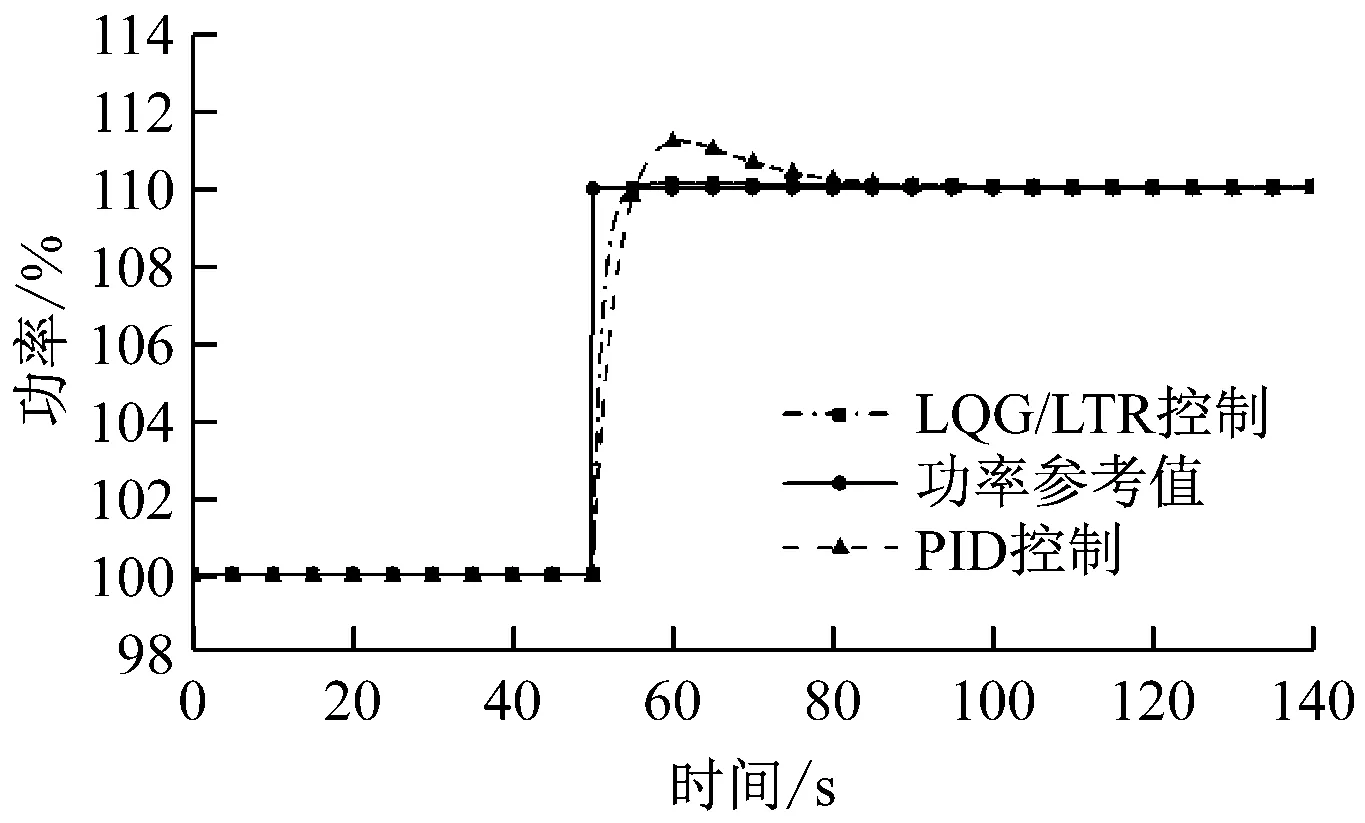
图8 功率参考值阶跃时的功率变化Fig.8 Variation of power in response to a step change of powerreference values
结合图8和图9可以看出功率参考值提高时控制棒动作导致的反应性变化曲线。从图9可以看出,由于LQG/LTR控制作用导致控制棒上提,引入的反应性最大为120×10-5。而在相同工况下,PID控制导致控制棒动作幅度更大,反应性最大达到190×10-5。

图9 功率参考值阶跃时的反应性变化Fig.9 Variation of reactivity in response to a step change of powerreference values
4 结 论
针对小型堆运行过程中的非线性、强耦合和强时变等特点,搭建了堆芯系统集总参数非线性模型。基于LQG/LTR控制设计了堆芯功率控制器。将该控制器与PID控制器的控制效果进行了对比分析。结果表明,LQG/LTR方法具有更好的抗干扰能力和负荷跟踪能力,且控制性能优于PID控制。
