基于CQPSO算法的含风电场电力系统经济调度研究

蒋 慧，戴文俊

基于CQPSO算法的含风电场电力系统经济调度研究

*蒋 慧1，戴文俊2

（1.淮南联合大学，安徽，淮南 232038；2.淮南师范学院，安徽，淮南 232038)

为了克服风电场出力波动的不利影响，提高调度经济性，构建含常规火力发电燃料费用、风电预测误差备用费用以及风电弃风成本的多目标动态调度模型，并提出一种混沌量子粒子群算法对模型进行求解。标准测试函数的仿真结果表明本算法比对照算法具有较高的收敛精度和稳定性。对含风电场的IEEE30节点系统算例进行仿真实验，结果表明采用混沌量子粒子群算法对调度模型求解的调度费用最低。

混沌；量子粒子群优化；动态经济调度；多目标优化；风电场

由于风电具有很强的随机性，所以风电穿透功率超过一定值之后，给并网带来明显的波动性和随机性，会严重影响电能质量和电力系统的运行。学者们主要通过持续法、卡尔曼滤波法、时间序列法及在此基础上的改进方法对风速和风电功率进行预测研究，不断提高风速预测精度，有效地减轻或避免风电场出力不确定对电力系统的不利影响。然而，风速预测的准确性受预测对象的规律性影响很大，目前预测误差一般在25%~40%左右。因此含有风电的电力系统经济调度不再是确定性问题[1-4]。为了克服风电随机性的影响达到经济调度的目的，学者们在传统调度模型的基础上进行了优化与改进研究。文献[4]提出了一种区间经济调度非线性对偶优化方法，将风电有功功率描述为区间数，建立乐观及悲观双层非线性经济调度优化模型。文献[5]以优先调度风电为基本原则，引入风功率弃风分段惩罚因子，建立计及电网安全的风火协调优化调度模型。文献[6]在调度模型中引入风能的期望出力与实际处理之差成正比的惩罚成本函数，并转化成和风能概率密度相关的积分形式来表示风能的随机性，从而确保风能得到充分利用。文献[7]在调度模型中引入正、负旋转备用约束，将火电机组阀点效应计及到发电总成本中以满足风电功率的波动性和预测误差对动态经济调度旋转备用的新要求。目前，对含风电场电力系统的调度模型求解算法主要采用人工智能算法，如遗传算法、免疫算法、蚁群算法、粒子群算法以及在此基础上的改进算法等[8-13]。其中，粒子群及其改进算法因通用性好，适合处理多种类型目标函数和约束而被广泛应用到电力系统调度模型的求解[12-13]。对于粒子群算法的改进，孙俊等结合量子力学相关理论提出了量子粒子群优化算法（QPSO），该算法已被证明是一个全局收敛的搜索算法[14]。文献[15]在此基础上提出了基于微分进化算子的量子粒子群优化算法（QPSO-DE），在粒子搜索过程中，以一定的概率对粒子的每一维执行微分进化操作，以增加粒子的随机性，从而减少了粒子群体因多样性缺失而易于陷入局部最优或停滞的情况，增强了粒子群体的搜索能力。但是文献[15]中对决定收敛性的扩张收缩因子采用区间线性递减的方式进行取值，会使得迭代前期的局部搜索能力弱，容易错过全局最优位置，而在迭代后期全局搜索能力变弱，容易陷入局部最优[16]。所以本文利用混沌算法的强初值敏感度和随机性的优点，通过生成混沌序列的方式产生扩张收缩因子取代线性递减函数构成一种混沌量子粒子群算法（CQPSO）。

综上所述，本研究构建以常规火力发电燃料费用、风电预测误差备用费用及风电弃风成本的多目标动态调度模型，采用混沌量子粒子群算法求解模型。

1 多目标调度建模

1.1 目标函数

本研究构建以常规火力发电燃料费用、风电预测误差备用费用以及风电弃风成本的多目标调度模型，具体如下：常规火力发电燃料费用成本：

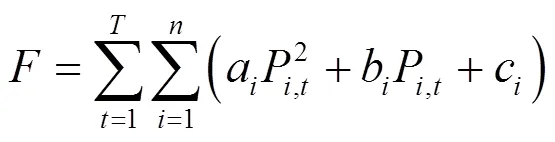
式中：P为常规火力发电机组在时段的有功输出，a，b，c为燃料费用成本系数。为研究周期内的小时数，本研究取24，即日经济调度。

在调度中，如果功率缺额不大，可以通过调节旋转备用输出进行平衡，无需启停。

风电并网所增加的备用容量是由于风能的随机性引起的，从而导致风电场期望出力与实际出力存在偏差，因此风电并网所增加的旋转备用容量费用可表示为[17]：

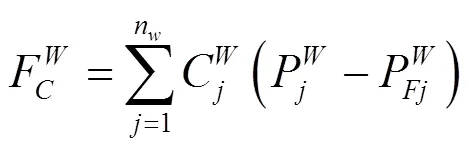
考虑电网的接纳能力，所以引入基于极限穿透功率的风电场弃风运行惩罚成本：

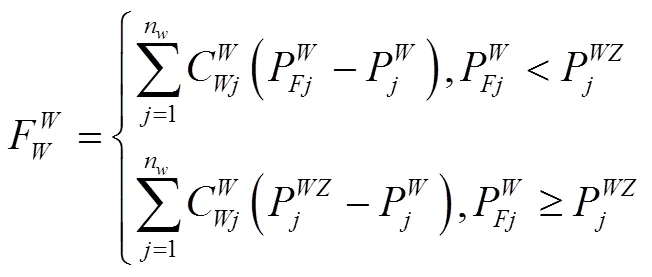
综上所述，构建以常规火力发电燃料费用、风电预测误差备用费用以及风电弃风成本的多目标调度模型，目标函数如式（4）。

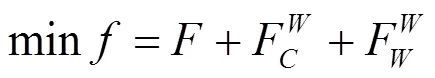
1.2 约束条件

1）功率平衡约束

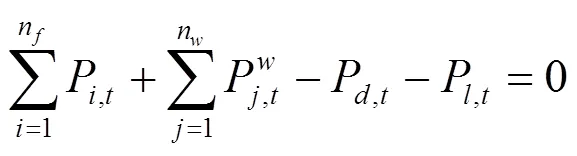
2）单机出力约束

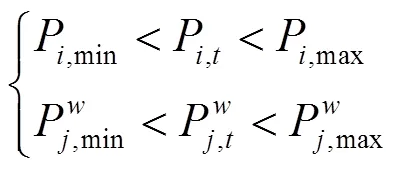
3）爬坡率约束

火力发电的有功出力跟随风机出力波动进行调节，但是要考虑火力机组的爬坡率，相邻时刻的有功出力变化低于爬坡率即

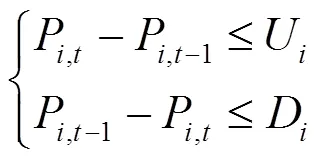
式中：U为向上爬坡率，D为向下爬坡率。

4）旋转备用约束

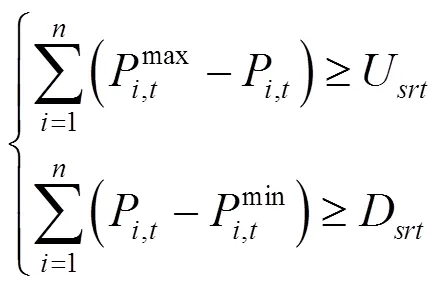
式中：D、U分别为系统在该时段的上、下旋转备用容量。

1.3 风电功率预测

为了简化计算，采用近似功率曲线直接转换风速预测值的方法对风机有功出力进行预测，近似模型如下：

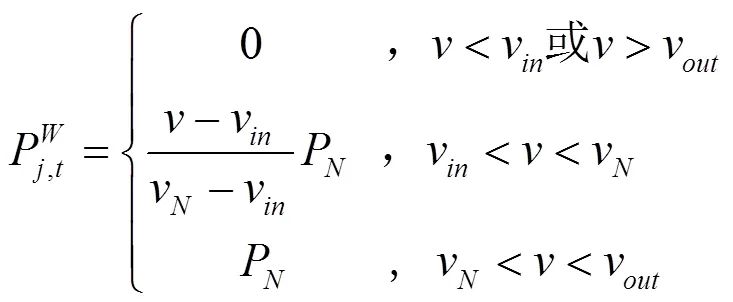
2 混沌量子粒子群算法

2.1 混沌量子粒子群算法

文献[15]提出的基QPSO-DE算法如公式（10）所示：

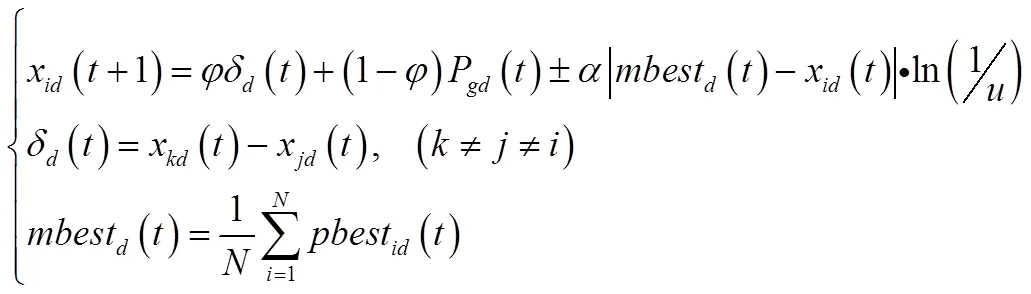
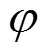
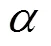
扩张收缩因子的混沌序列采用Logistic映射模型[18]：

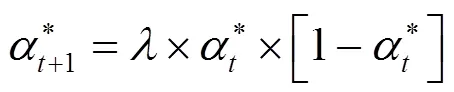
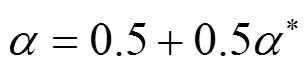
通过上述分析，得到混沌量子粒子群算法的执行流程如图1所示。图中的为[0,1]区间设置的常数，旨在进化每一维度粒子时，以一定概率执行公式（10）公式中的“+”或“-”，本算法取=0.5。

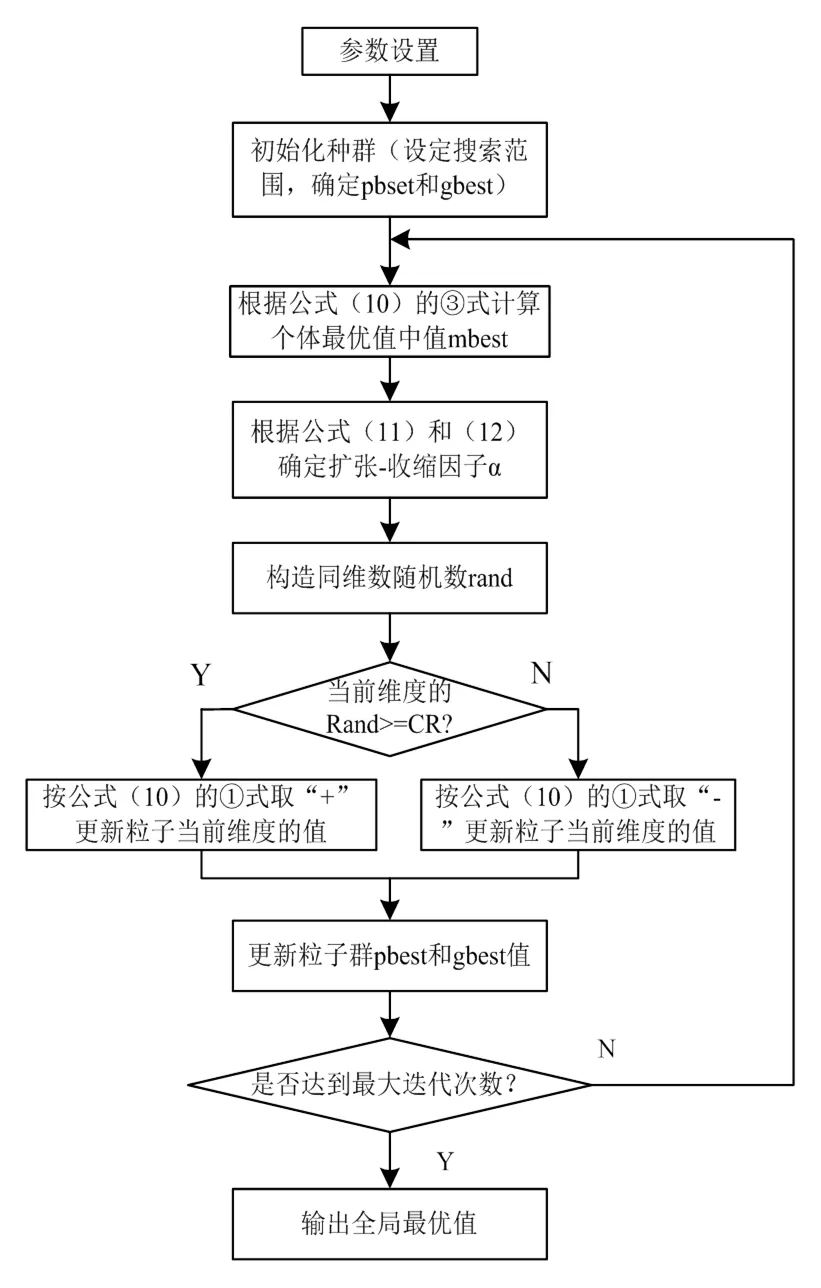
图1 混沌量子粒子群算法执行流程图

2.2 标准测试函数求解与分析

为了测试和比较本文提出的混沌量子粒子群算法的性能，同时采用基于微分的量子粒子群（QPSO-DE）算法[15]和改进量子粒子群（IQPSO）算法[19]做为对比，分别对表1所示的3个标准测试函数进行最值求解（全局最小值均为0），在种群规模均为50的条件下以迭代次数1000和2000各运行50次，取最优值、平均值并计算标准差，测试结果对比如表2所示。为了方便对比收敛速度，在迭代次数为1000的运行结果中，取前100次迭代绘制50次运行的适应度平均收敛曲线如图2所示。

表1 标准测试函数

Table 1 Standart test function

函数名称测试函数搜索范围维度 sphere30 Schwefel30 Rastrigin30

表2 各算法测试结果对比

Table 2 Comparison of test results of each algorithm

测试函数迭代次数评价指标QPSO-DEIQPSOCQPSO f11000最优值8.2839e-2021.0555e-1981.0382e-218 平均值4.43258e-1004.22530e-897.0442e-103 标准差3.10275e-997.5235e-884.8292e-102 2000最优值0（12次）0（5次）0（35次） 平均值6.7051e-2411.3391e-1891.6569e-256 标准差000 f21000最优值1.14183e-833.0148e-642.55486e-100 平均值1.00859e-457.8154e-347.61035e-51 标准差7.05653e-451.4729e-334.50937e-50 2000最优值9.1026e-1814.3331e-1611.1432e-205 平均值3.3986e-1132.4780e-1128.2761e-124 标准差01.7426e-1454.0946e-123 f31000最优值0（44次）0（39次）0（46次） 平均值1.0027e-1336.5789e-1301.8271e-151 标准差6.7302e-1335.41586e-1314.0694e-152 2000最优值0（48次）0（43次）0（49次） 平均值6.7247e-1711.5402e-1553.1540e-188 标准差02.1683e-1540

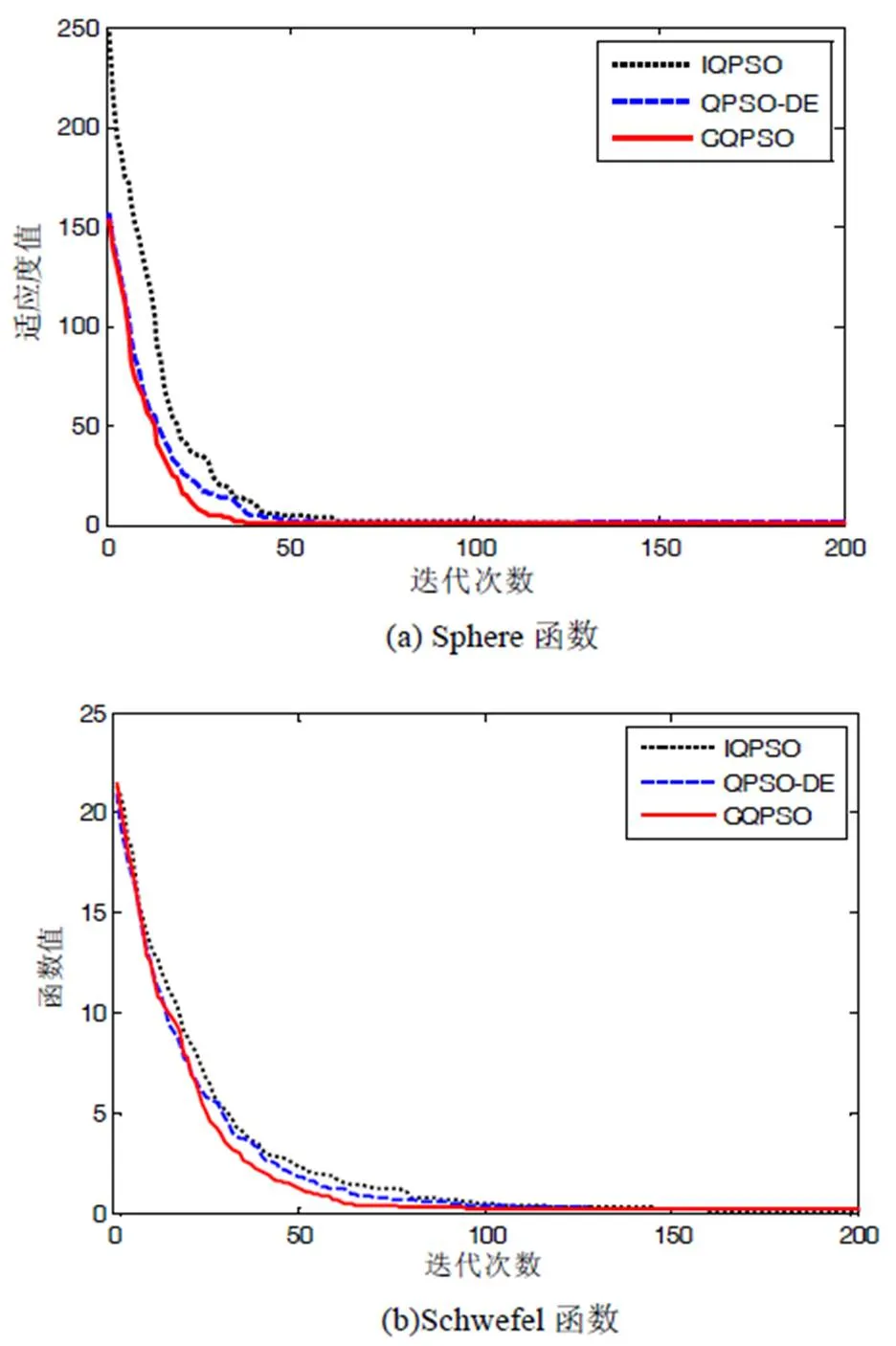
由表2可知，3个测试函数的极值均为0，本文算法的最优值以及50次仿真结果最优值的平均值均小于对比算法，说明本文算法的收敛精度优于对比算法。通过测试函数1和3的最优值可以看出，本文算法在不同迭代数的情况下，出现最优值为0的次数均多于对比算法，说明针对上述测试函数，本文算法的稳定性优于对比算法。图2所示的收敛曲线显示出本文算法求解本次测试函数的收敛速度优于对比算法。

3 算例分析

本研究在IEEE30节点标准测试系统基础之上进行修改作为本文算例进行仿真分析，即在节点17接入一个风电机组，其中风场总容量为40MW（20台单机容量为2MW的双馈风力发电机）；设常规机组的参数如表3所示，将对含风电场的多目标调度模型作为混沌量子粒子群算法的目标函数进行求解，基准值均取100MVA。为了验证调度模型的优越性，以Weibull模型为预测风速，在此基础上添加波动作为实际风速，模拟风速预测误差。设置切出风速为v=30m/s，切入风速v=5m/s，额定风速为v=15m/s。考虑IEEE30节点标准测试系统为一个整体，所以对各节点负荷进行等效计算，得各时段系统总负荷如表4所示。功率等式约束条件的线路损耗按照总负荷的5%估算，火力机组的上下爬坡率分别设为2%/min和5%/min，上下旋转备用容量取总负荷的5%。

表3 常规机组相应参数

Table 3 Corresponding parameters of conventional units

机组有功上限/pu有功下限/pu额定功率/puai（$/MW2h）bi（$/MWh）ci（$/h） 11.650.901.500.236.356726.889 21.200.451.000.343.515905.338 50.600.180.500.0838.9331002.874 80.600.290.500.0535.3041124.385 110.300.120.250.0933.2381543.653 130.300.120.250.1234.2681304.569

表4 各时段系统总负荷（单位：pu）

Table 4 Total system load in each period(unit:pu)

时段123456789101112 负荷2.9032.8752.9172.9672.9722.7443.1573.3473.8923.8213.8203.792 时段131415161718192021222324 负荷3.6923.8923.6363.6643.8013.8433.8343.7123.5873.3253.1092.875

本算例的混沌量子粒子群算法设置粒子群规模为100，迭代2000次。求解得平均日费用最小值为66.92万美元。在相同粒子群规模和迭代次数的条件下，采用基于微分量子粒子群（QPSO-DE）算法的费用最小值为70.41万美元，采用改进量子粒子群（IQPSO）算法求得费用最小值为81.09万美元。上述结果表明本文算法对模型求解的费用最低。表5列出了混沌量子粒子群算法求解含本算例调度模型日费用最小时随风电场出力波动对应的各常规发电机的有功出力。

绘制目标函数的前100次迭代自适应度平均收敛曲线如图3所示，通过比较可知，混沌量子粒子群算法的收敛精度更高。

表5 最优解对应的各发电机输出（单位：pu）

Table 5 The output of each generator corresponding to the optimal solution(unit:pu)

时段G1G2G3G4G5G6W时段G1G2G3G4G5G6W 11.0060.6660.2120.4620.1770.1800.201131.3080.8350.3620.4690.1860.1600.372 21.0750.6730.2350.4160.1290.1240.223141.4150.8720.4010.4330.2070.2020.362 31.1070.6320.2010.4290.1420.1540.252151.3070.8020.3590.4220.2030.2090.334 41.1810.6910.1830.3250.2070.1260.254161.3130.7870.2930.4820.2260.2060.357 51.1500.4820.2900.3710.2330.1430.303171.3820.6820.3930.4720.2510.2370.384 60.9420.4350.2450.4010.2390.1450.337181.4710.7820.3610.4340.2040.2020.389 71.1550.5730.2060.3920.2150.1950.351191.4970.8830.2980.3730.2070.2010.375 81.2090.7020.3580.3720.2080.1710.327201.4090.7810.3670.3760.2160.2100.353 91.3300.8750.3620.4920.2410.2210.371211.3430.7630.3030.4270.2140.1980.339 101.2390.8610.4330.4820.2210.2070.378221.2280.6720.2970.4320.2030.1840.309 111.3070.8470.3850.4690.2050.2100.397231.1730.5690.2030.4190.1840.1800.381 121.3230.8230.4460.3990.2300.1750.396241.0340.4630.2410.3790.1880.1840.386

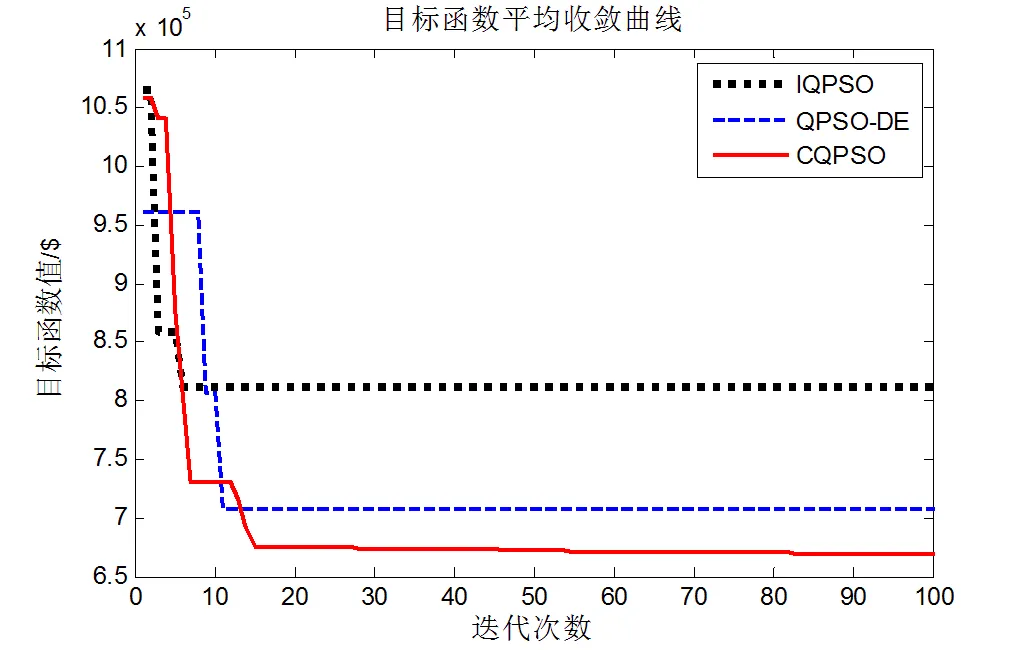
图3 调度模型收敛曲线图

4 结论

本研究构建了以常规火力发电燃料费用、启停费用、风电预测误差旋转备用费用以及风电弃风成本为目标函数的含风电场电力系统多目标经济调度模型，提出混沌量子粒子群算法对模型进行求解。通过对含风电场的IEEE30节点系统算例分析，证明了采用混沌量子粒子群算法对本调度模型求解克服了风电场出力的随机性对电力系统调度的不利影响，具有较高的收敛精度，达到了经济性调度目的。本研究考虑到风电场容量较小，常规机组的旋转备用容量相对充足，没有考虑常规机组的启停问题。不足之处是未考虑风电的运行维护成本等，这是后续研究的方向。

[1] Alexiadis M,Dokopoulos P, Sahsamanoglou H et al．Short term forecasting of wind speed and related electrical power[J]. Solar Energy, 1998, 63(1): 61-68．

[2] 杨秀媛,肖洋,陈树勇. 风电场风速和发电功率预测研究[J]. 中国电机工程学报,2005,25(11):1-5.

[3] 孙元章,吴俊,李国杰,等. 基于风速预测和随机规划的含风电场电力系统动态经济调度[J]．中国电机工程学报,2009,29(4):41-47.

[4] 周玮,胡姝博,孙辉,等. 考虑大规模风电并网的电力系统区间非线性经济调度研究[J]．中国电机工程学报,2017,37(2):557-563.

[5] 徐帆,王颖,杨建平,等. 考虑电网安全的风电火电协调优化调度模型及其求解[J]．电力系统自动化,2014,38 (21):114-120.

[6] HetzerJ, Yu D C, BhattaraiK. An economic dispatch model incorporating wind power[J]. IEEE Transactions on Energy Conversion,2008,23(2):603-611.

[7] 周玮,彭昱,孙辉,等. 含风电场的电力系统动态经济调度[J]．中国电机工程学报,2009,29(25):13-18.

[8] 汤晓青,刘辉,范宇,等．基于改进多目标遗传算法的实时发电市场优化调度研究[J]．电力系统保护与控制,2017,45(14):65-71.

[9] 程启明,黄山,程尹曼,等. 基于改进型量子遗传算法的微网经济优化运行[J]．高压电器,2018,54(3):136-145.

[10] 周德建,杨莉,郭文明. 基于免疫算法的水火电联合调度模型[J]．水力发电学报,2013,32(2):95-100.

[11] 李小林,张松,陈华平. 考虑分时电价的多目标批调度问题蚁群算法求解[J]．中国管理科学,2014,22 (12):56-64.

[12] 卢锦玲,苗雨阳,张成相,等. 基于改进多目标粒子群算法的含风电场电力系统优化调度[J]．电力系统保护与控制,2013,41(17):25-31.

[13] 牛文静,冯仲恺,程春田. 梯级水电站群优化调度多目标量子粒子群算法[J]．水力发电学报,2017,36(5):47-57.

[14] Sun Jun,Feng Bin,Xu Wenbo. Particle swarm optimization with particles having quantum behavior[C]. Proceedings of the 2004 Congress on Evolutionary Computation,2004:325-331.

[15] 方伟,孙俊,须文波. 基于微分进化算子的量子粒子群优化算法及应用[J]．系统仿真学报,2008,20(24): 6740-6744.

[16] 陈义雄,梁昔明,黄亚飞. 一种改进的混沌量子粒子群优化算法[J]．计算机工程,2013,39(8):253-256.

[17] 聂永辉,王中杰,李江,等. 大规模风电并网电力系统优化潮流[J]．太阳能学报,2017,38(11):3180-3187.

[18] 陈志刚,梁涤青,邓小鸿,等. Logistic混沌映射性能分析与改进[J]．电子与信息学报,2016,38(6):1547-1551.

[19] 陈功贵,黄山外,孙志,等. 基于改进量子粒子群算法的电力系统经济调度仿真研究[J]．实验技术与管理,2017, 34(3):104-107.

RESEARCH OF ECONOMIC DISPATCH OF POWER SYSTEM WITH WIND FARMS BASED ON CHAOS QUANTUM PARTICLE SWARM OPTIMIZATION ALGORITHM

*JIANG Hui1，DAI Wen-jun2

(1. Huainan Union University, Huainan, Anhui 232038, China; 2. Huainan Normal University, Huainan, Anhui 232038, China)

In order to overcome the adverse effects of wind farm output fluctuation and improve the scheduling economy, a multi-objective dynamic scheduling model including conventional thermal power fuel cost, wind power prediction error reserve cost and wind power abandonment cost were constructed, and a chaos quantum particle swarm optimization algorithm was proposed to solve the model. The simulation results of the standard test function showed that the algorithm had higher convergence accuracy and stability than the control algorithm. The simulation results of IEEE30-node power system with wind farm showed that the scheduling cost of using chaotic quantum particle swarm optimization algorithm to solve the scheduling model was the lowest.

chaos; quantum particle swarm optimization; dynamic economic dispatch; multi-objective optimization; wind farms

TM734

A

10.3969/j.issn.1674-8085.2021.01.013

1674-8085(2021)01-0076-06

2020-09-11；

2020-11-26

安徽省高校优秀青年人才支持计划重点项目（gxyqZD2018099）；安徽省高校自然科学研究项目（KJ2020A0898）；淮南师范学院科学研究重点项目（2019XJZD06）；淮南联合大学科学研究项目（LYB1702）

*蒋 慧(1985-)，女，安徽全椒人，副教授，硕士，主要从事电力系统智能控制方面研究(E-mail：aaa-jhui@163.com)；

戴文俊(1987-)，男，安徽长丰人，讲师，硕士，主要从事电力电子与电气传动控制研究(E-mail：dwjkaoyan@163.com);