超声场中振荡微泡对血管壁的生物力学效应

刘文一，胡继文，刘亚涛，雷卫瑞，陈学坤

超声场中振荡微泡对血管壁的生物力学效应

刘文一，*胡继文，刘亚涛，雷卫瑞，陈学坤

(南华大学数理学院，湖南，衡阳 421001)

血管内受束微泡振荡所产生的生物力学效应在靶向药物传递、开放血脑屏障等具有重要的医学应用。本文从生物力学角度，创建了一个气泡-流体-固体耦合动力学模型，利用有限元法，研究超声场中振荡微泡与血管壁的相互作用，得到不同超声频率、血管尺度及不同初始半径微泡对血管壁的应力及应变分布。结果表明：频率1.0~1.5MHz时，血管壁应力随频率增大而降低；1.5~2.0MHz时，应力随频率经历半个正弦波形的变化，2.0 MHz之后不同初始半径微泡对血管壁的应力趋向一个相等的稳定值；当频率和初始微泡确定时，血管壁应力随血管半径先增大后变小,血管越厚，其应力和振动幅值都相应变小。三种不同初始半径微泡在不同血管半径中能产生有相应的应力极大值，其中较小初始半径微泡应力最大。本模型可用于计算不同声参数、血管尺度及不同初始微泡半径时的生物力学效应，为血管损伤评估提供参考。

超声；微泡； 微血管； 应力； 有限元法质

随着对微泡的空化效应等特性的深入了解，其在生物医学领域的应用也越来越受关注，尤其是利用微泡在生物壁面产生的生物力学效应，如声孔效应等，使其在靶向药物传递/基因药物治疗等领域得到了较大的发展[1]。理论和实验表明，在超声作用下，微泡在生物壁面附近振荡会在其周围产生微射流，微射流在生物壁面产生的剪切力可使细胞膜破裂，导致细胞膜壁面通透性增加，产生瞬时可逆性或不可逆性孔隙，形成所谓的声孔效应[2]。

目前关于超声场中的微泡空化有两种假设:一是瞬态空化，即超声微泡表现剧烈的非线性振荡和不可控制，并在局部产生高温、高压现象，对细胞形成不可逆性损伤；二是稳态空化，即超声微泡在平衡半径附近作近周期性振荡，因而细胞膜的功能性损伤较小[3]。然而，要安全地将声孔效应应用到生物和医疗领域，须理解并掌握超声微泡在生物壁面附近振荡时对壁面损伤的物理机制。早在1958年Nyborg给出了振荡的微泡稳态下由微流产生剪切力的近似解[4]。基于该理论，Rooney计算出了超声微泡振荡产生的微流作用在平直壁面的剪切力分布[5]。Nyborg 主要针对微泡紧贴生物壁面的情况，但实际上微泡与生物壁面之间存在一定的距离。为此Krasovitski和Kimmel利用边界积分法计算了剪切力在平直壁面上微射流及切向应力分布情况[6]。Wiedemair等计算了血管内超声造影剂在其破裂时在血管壁上产生应力峰值，并导致血管壁破裂[7]。Miao等利用边界元法研究了血管内微泡受血管壁尺度及声参数对微泡振荡半径及形成微射流分布影响[8]，陈楚怡等利用有限元软件分析了微血管内微泡振荡受微泡本身材料、血管尺度及血管材料的影响，并对振荡微泡在壁面某特定位置应力随时间变化进行了描述[9]。Bahrami等借助有限体积法分析微管内微泡振荡对血管壁所形成的压力及微泡本身尺度变化情况分析[10]。Miller等在实验中利用高速摄像技术得到微血管内微泡的振荡引起血管收缩和肿胀，同时观察到微泡产生的微射流给血管壁带来损伤[11]。借助造影的空化效应，Nove等监测超声诱导微泡空化在疏通血脑屏障过程中的细节[12]。理论和实验表明，超声作用下，不同声参数及不同微泡对血管壁作用都存在不同程度的影响。

实验上微血管内微泡振荡对血管壁损伤问题的研究所需仪器精度要求较为苛刻，且具有不易观测、耗时长和成本高等特点。数值计算具有快速、灵活模拟不同条件下振荡微泡对血管壁作用过程的优势。目前数值计算方面，对超声微泡在生物壁面的力学效应研究大多集中于对微泡本身受生物壁面的影响分析，对弹性血管内的微泡振荡引起血管形变及应力分布方面的研究相对较少。本文基于生物力学原理，创建了一个气泡-流体-固体耦合模型。假设微泡呈球形振荡、血管壁为均匀的各向同性的线弹性材料，利用有限元法，研究了超声作用下微泡振荡对血管壁的影响。重点研究了不同超声频率、血管半径和血管壁厚度下微泡对附近血管壁应力和应变的分布，并对计算结果进行了总结。

1 材料与方法

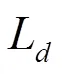
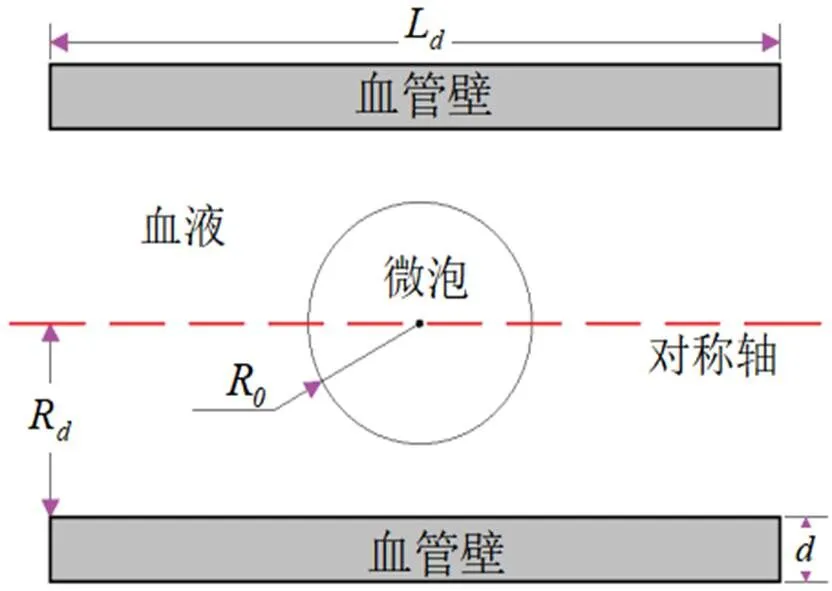
图1 气泡-流体-固体耦合模型图

1.1 管内微泡动力学方程

受束于粘滞流体中的弹性微血管内的微泡，考虑到微血管的长度和半径影响时，其动力学方程可表示为[13]：

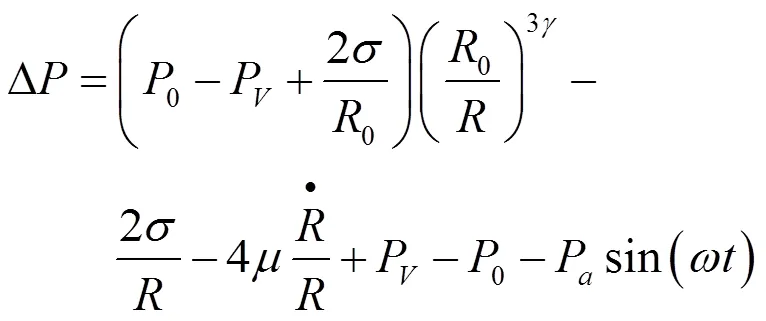
1.2 流体模型

假设血液是不可压缩流体，血流动力学满足Navier-Stokes方程[14]：

1.3 固体模型

设血管壁是均匀的各项同性的线弹性材料，忽略其体积力时，血管壁的位移随时间形变的动力学过程可用如下方程表示[14]:

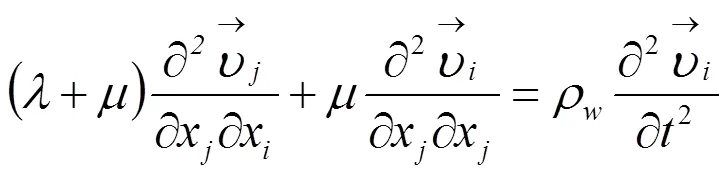
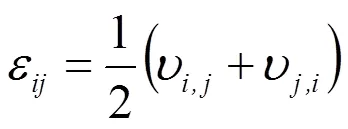
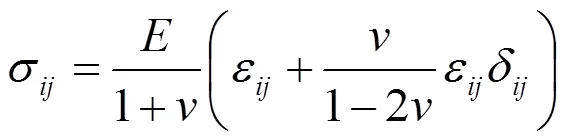
1.4 边界条件

气泡-流体-固体模型中需构造气泡-流体和流体-固体间的两个作用边界。在气泡-流体间的作用中，满足质量和动量守恒，相应的动力学方程可表示为[16]：

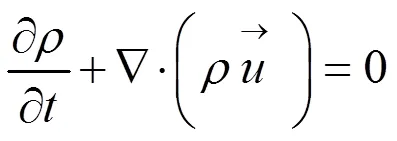
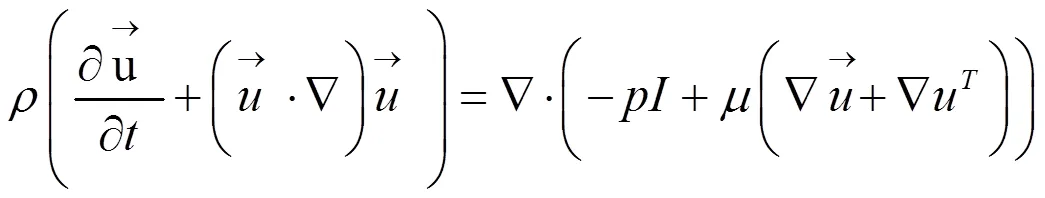
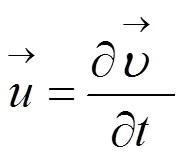
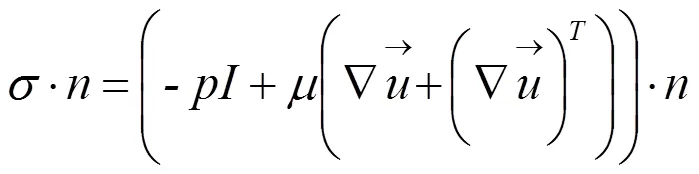
2 结果与分析

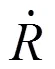
表1 模型参数

Table 1 Parameters of the geometry model

名 称参数数值/单位 气体多方指数 γ1.07 饱和蒸汽压PV2330Pa 微泡初始半径R02μm 气液表面张力σ0.056 N/m 血液密度ρ1059kg/m3 声压Pa0.1 MPa 血液动力粘度μ0.0035Pa·s[18] 血管密度ρw1000kg/m3 血管杨氏模量E3 MPa[18] 血管泊松比v0.49[18]

2.1 血管厚度对血管壁的力学效应

图2表示血管半径8 μm、超声频率1MHz时三种不同血管壁厚度对应的振动微泡对血管壁最大应力、应变的响应。图2(a)为厚度1 μm[18]微泡引起的射流及在血管壁上引起的最大应力二维分布。由图得知，在离微泡最近的血管壁区域内应力分布较大，应力峰值为0.528 MPa。随偏离中心应力逐渐变小，应力相对中心近似于正态分布。1.5 μm[18]和2.0 μm[18]下的应力峰值分别为0.375 MPa和0.326 MPa。随着血管厚度的增加，血管壁受到的应力减小。

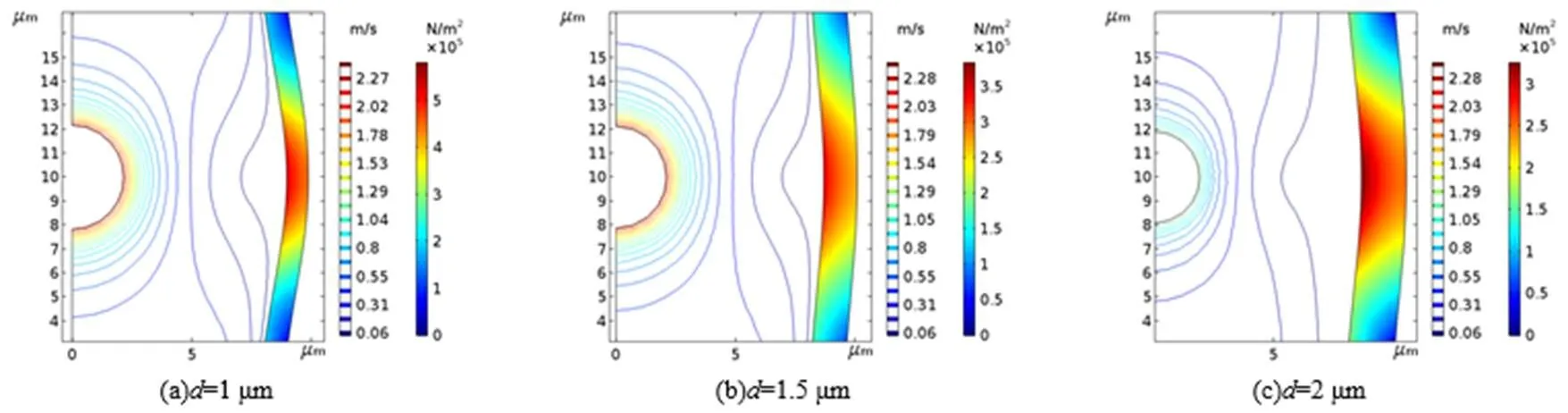
图2 不同壁厚度下微泡附近血管壁最大应力云图

图2中三种血管厚度对微泡振荡所引起的射流速度相差不大。如图2中(a)、(b)和(c)所示，分别2.39 m/s、2.4 m/s和2.4 m/s，但血管壁的振荡位移随血管壁厚度增加而降低。厚度=1.0 μm时振动最大位移接近1.0 μm，而1.5 μm和2.0 μm时振动位移分别为0.5 μm和0.3 μm。可见，超声场中血管厚度增加，所受微泡振荡的影响变小，可减少血管损伤。

2.2 血管管径对血管壁的力学效应

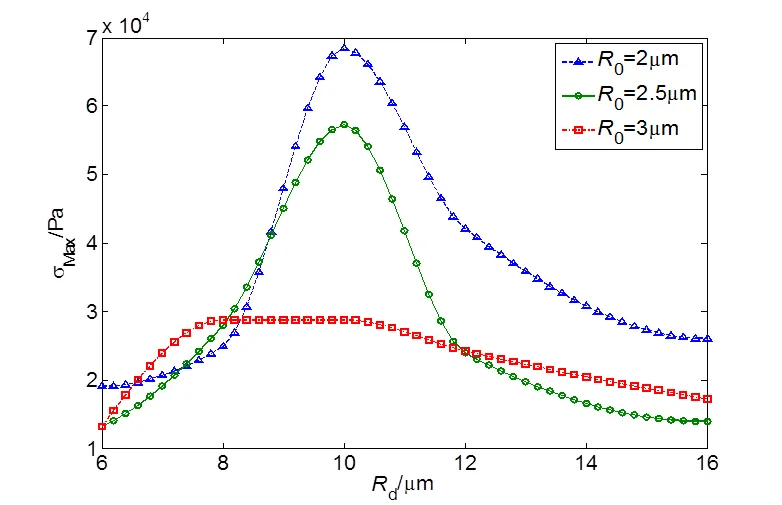
图3 不同血管半径下三种初始半径微泡对血管壁的最大应力线图

图3表示超声频率为1MHz、血管厚度1.5 μm时血管壁最大应力随血管半径变化曲线，血管壁在收缩和膨胀各存在一个最大应力峰值，图中取两值的平均数作为最大应力值。由图可知，初始半径为2.0 μm的微泡在不同管径下对血管壁产生的应力峰值最大，在血管半径为10.0 μm下的最大峰值为0.069 Mpa。初始半径为2.5 μm和3.0 μm的微泡分别在血管半径为9.0 μm和8.8 μm时达到峰值，分别为0.057 MPa和0.028 MPa。另外，根据图4可知，微泡初始半径相对于血管半径越小，超声作用下微泡受到血管壁的限制减小，振荡更为剧烈，其周围产生的微射流速更大。相比0=2.5 μm和0=3.0 μm的微泡，0=2.0 μm时的振荡微泡在R=10 μm下的振荡速度高达4.1 m/s，对血管壁产生的应力更大，其带来的损伤也相应要大。当血管半径超过10 μm时，根据图3和图4，虽然微泡的振荡的最大速度仍在增大，但其血管半径的影响超过了微射流的影响，血管壁的最大应力开始减小。由于初始半径3.0 μm的微泡相对距离血管壁较近，最大应力减小趋势弱于初始半径为2.0 μm和2.5 μm下的微泡。

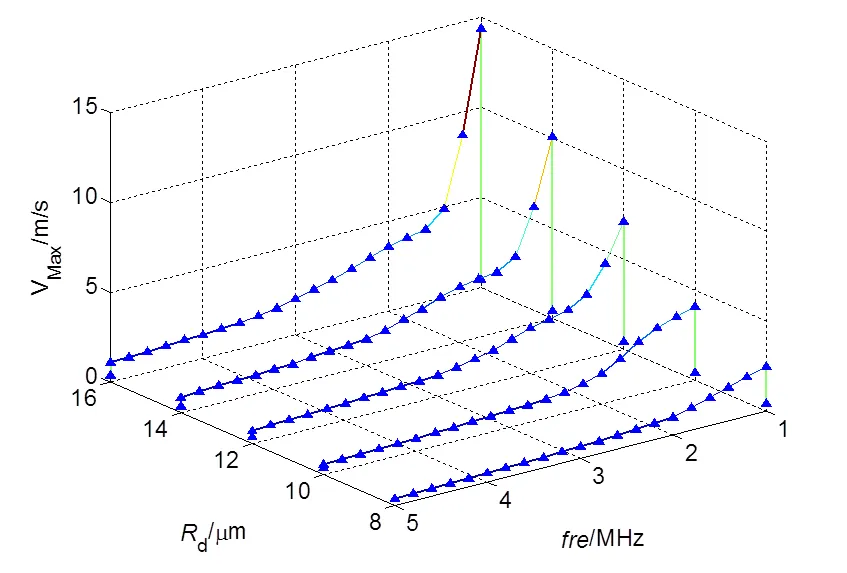
图4 初始半径2μm微泡振荡引起的最大射流速度随超声频率和血管半径变化曲线

2.3 超声频率对血管壁的力学效应

图5表示血管半径为8 μm、血管壁厚度1.5 μm时，不同超声频率下三种微泡对血管壁最大应力响应。血管壁在收缩和膨胀阶段各存在一个最大应力值，图中是取两值的平均作为最大应力值。由图观察得到，三种初始半径微泡对血管壁的应力都是随着超声频率增大而减少。这一结果可从图4中得到解释：随着超声频率增加，微泡的振荡减弱，其产生的射流速度会相应减小；但当微泡初始半径与血管半径之比减小时，微泡的振荡速度在增加，故图5中在初始半径为2 μm下的微泡在不同超声频率下对血管壁产生的法向应力相对要大。在1.5 MHz下的超声频率下，三种微泡对血管壁产生的最大应力分别为0.103 MPa、0.093 MPa和0.083 MPa，呈递减趋势。

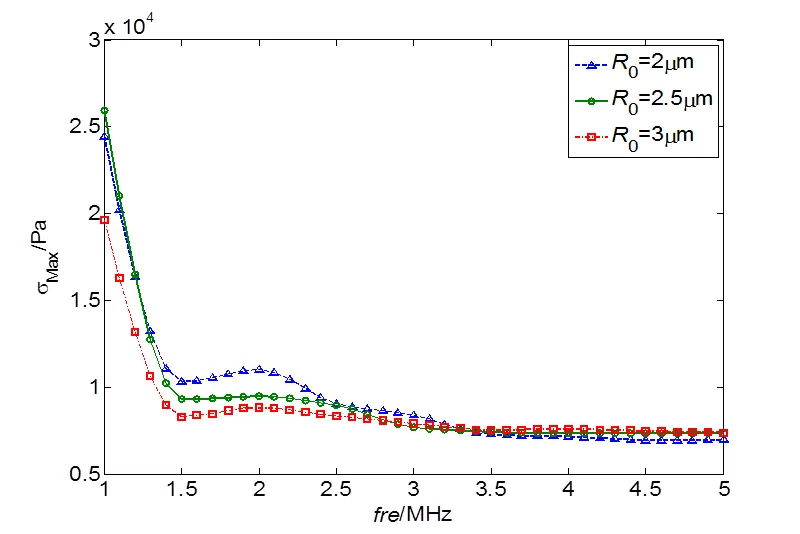
图5 不同超声频率下三种初始半径微泡对血管壁的最大应力线图

当频率从1.5 MHz加到2 MHz时，三种情况下，血管壁受到的最大应力相对于1.5 MHz分别增加了0.0073 MPa,0.0018 MPa和0.0051 MPa,血管壁的振荡频率接近于微泡的振荡频率，所以血管壁的最大应力呈上升趋势。当超声频率超过3.5 MHz时，如图5所示，三条曲线保持基本一致，超声频率的影响超过了微泡初始半径的影响，R=3 μm的微泡距离血管相对较近，最大应力曲线在其它曲线上方。可知，在超声激励下，频率越低，血管损伤越大，声孔效应越显著。

3 结论

本文依据血流动力学原理，建立了一个二维轴对称气泡-流体-固体耦合模型，借助有限元法，计算了超声激励下微泡振荡及其与血管壁间的相互作用过程。由微泡振荡激发微射流，并作用于附近血管壁面产生相应的应力和应变。应力主要集中在距微泡最近血管壁上，使得该区域壁面最先受到损伤。微泡振荡受外部驱动频率、微泡初始半径及血管尺度等因素影响，从而影响其附近血管壁的应力和应变等生物力学效应。总之，利用本文模型，可计算不同参数下超声协同微泡作用于壁面的应力和应变分布。如调节适当的声参数，或可使其生物力学效应得到更为广泛的应用。

[1] 王顺义,李怡. 超声微泡介导靶向治疗研究进展[J].医学与哲学, 2017, 38(1): 61-64.

[2] Kooiman K, Roovers S, Langeveld SAG, et al. Ultrasound-Responsive Cavitation Nuclei for Therapy and Drug Delivery [J]. Ultrasound Med Biol. 2020, 46(6): 1296-1325.

[3] Movahed P, Kreider W, Maxwell AD, et al. Cavitation-induced damage of soft materials by focused ultrasound bursts: A fracturese bubble dynamics model [J]. J Acoust Soc Am., 2016, 140(2): 1374-1386.

[4] Nyborg W L. Acoustic Streaming near a Boundary [J]. J Acoust Soc Am. 1958, 30(4): 329-339.

[5] Rooney J A. Shear as a Mechanism for Sonically Induced Biological Effects [J]. J Acoust Soc Am., 1972, 52(6): 1718-1724.

[6] Krasovitski B, Kimmel E. Shear stress induced by a gas bubble pulsating in an ultrasonic field near a wall [J]. IEEE Trans Ultrason Ferroelectr Freq Control., 2004, 51(8): 973-979.

[7] Wiedemair W, Tukovic Z, Jasak H, et al. The breakup of intravascular microbubbles and its impact on the endothelium [J]. Biomech Model Mechanobiol., 2017, 16(2): 611-624.

[8] Miao H, Gracewski SM, Dalecki D. Ultrasonic excitation of a bubble inside a deformable tube: Implications for ultrasonically induced hemorrhage [J]. J Acoust Soc Am., 2008, 124(4): 2374-2384.

[9] Chuyi C, Yuyang G, Juan T, et al. Microbubble oscillating in a microvessel filled with viscous fluid: A finite element modeling study [J]. Ultrasonics. 2016 ,66: 54-64.

[10] Peng KCC, Singhose W. Low-oscillation command switch-times for relay-driven cranes with asymmetrical acceleration and deceleration [C]. Control Conference (ASCC), 2013 9th Asian. IEEE. 2013 :1-6.

[11] Miller D L, Lu X, Fabiilli M, et al. Influence of Microbubble Size and Pulse Amplitude on Hepatocyte Injury Induced by Contrast-Enhan ced Diagnostic Ultrasound [J]. Ultrasound Med Biol., 2019, 45(1): 170-176.

[12] Novell A , Kamimura HAS , Cafarelli A , et al. A new safety index based on intrapulse monitoring of ultra-harmonic cavitation during ultrasound-induced blood-brain barrier opening procedures [J]. Sci rep., 2020, 10(1): 1-12.

[13] Wiedemair W, Tukovic Z, Jasak H, et al. On ultrasound-induced microbubble oscillation in a capillary blood vessel and its implications for the blood-brain barrier [J]. Phys Med Biol, 2012, 57(4): 1020-1024.

[14] 戴苏秦,钱盛友,桂要生,等. HIFU治疗中血流对加热影响的仿真研究[J].系统仿真学报,2015,27(5):959-964.

[15] Carstensen E L, Parker K J. Physical models of tissue in shear fields [J]. Ultrasound Med Biol., 2014, 40(4): 655-674.

[16] Dukhin A S, Goetz P J. Fundamentals of Acoustics in Homogeneous Liquids [J]. Studies in Interface ence., 2010, 24: 91-125.

[17] Hosseinkhah N, Hynynen K. A three-dimensional model of an ultrasound contrast agent gas bubble and its mechanical effects on microvessels [J]. Phys in Med Biol. 2012, 57(3): 785-808.

[18] 王练妹,胡继文,雷卫瑞,等. 动脉粥样硬化斑块在血流作用下的应力分析[J].井冈山大学学报:自然科学版,2020,41(1):16-20.

[19] 武小岗,宋卫军,高东梅,等. 立体定向射频温控热凝术与微血管减压术治疗三叉神经痛的效果对比[J].湖南师范大学学报:医学版,2019,16(3):27-29.

BIOMECHANICAL EFFECTS ON BLOOD VESSEL WALL PRODUCED BY OSCILLATING MICROBUBBLE IN ULTRASOUND FIELD

LIU Wen-yi,*HU Ji-wen, LIU Ya-tao, LEI Wei-rui, CHEN Xue-kun

(Institute of Mathematical, Universityof South China, Hengyang, Hunan 421001,China)

The biomechanical effects produced by oscillating microbubbles confined in blood vessel play an important role in medical applications such as targeted drug delivery, blood-brain barrier opening etc. Based on the biomechanical mechanism, a bubble-fluid-solid coupling model was constructed. The interaction between a microbubble and vessel wall was investigated by finite element method. We calculated the stress distribution of the vessel wall produced by oscillating microbubble at different parameters. The results showed that the stress of wall decreased with increasing of frequency from 1.0 to 1.5 MHz. There was a shape of a half sine wave as the frequency changes from 1.5 to 2.0 MHz. The stresses tended to reach a stable value after 2.0 MHz, when the frequency and initial micro vesicles were determined, the stress showed a trend of first increase and then decrease with the radius of microvascular. The thicker the vessel, the smaller the stress and deformation got. Microbubbles with three different initial radii could produce corresponding maximum stress in different vessel radii, and the microbubbles with smaller initial radii had the largest stress. The model can be used to calculate the biomechanical effects at different acoustic parameters, vessel sizes and initial microbubble radii, which provides reference for vascular injury assessment.

ultrasound; microbubble; microvascular; stress; finite element method

O 411.03

A

10.3969/j.issn.1674-8085.2021.01.003

1674-8085(2021)01-0014-06

2020-10-09；

2020-11-17

国家自然科学基金项目(11747121，11904161)，湖南省教育厅重点科研项目(14A127)

刘文一(1995-)，男，河南安阳人，硕士，主要从事医用物理研究(E-mail:2607400551@qq.com);

*胡继文(1971-)，男，湖南衡阳人，副教授，博士，硕士生导师，主要从事医用物理研究(E-mail:hu_sanping@163.com);

刘亚涛(1994-)，男，河南周口人，硕士，主要从事医用物理研究(E-mail:1526243685@qq.com);

雷卫瑞(1998-)，男，湖南娄底人，硕士，主要从事医用物理研究(E-mail:leiweir@163.com);

陈学坤(1987-)，男，湖南衡阳人，副教授，博士，硕士生导师，主要从事超声物理研究(E-mail:813112490@qq.com).