不同船舶目标电磁散射仿真

陈立媛 ,杨神化,索永峰,陈文科

(集美大学航海学院，福建 厦门 361021)

0 引言

近年来，以海平面为背景的电磁散射特性研究受到人们的重视[1-4]。对于复杂电大尺寸目标的电磁散射问题，RCS(radar cross section)的求解算法可大致分为三类：精确解析法、数值计算、高频近似算法[5-6]。文献[7]运用前后向迭代数值算法(forward backward method,FBM)对舰船目标模型进行仿真计算；文献[8]采用数值计算方法对一维海平面摆动目标的散射特性展开研究；文献[9]选择(method of moments,MoM)融合(multi level fast multipole method,MLFMM)算法并行计算的混合全波数值算法，实现目标散射数据的获取。从船舶设计结构来说，不同类型的船舶具有不同的分布结构，船体大小、上层建筑的分布、船首和船尾的结构设计等都影响着目标电磁散射的结果。姜斌琦等[10-12]研究了船舶上层建筑、船首等的散射性能；朱雪慧等[13]设计了一款仿真软件对不同类型舰船进行全方位RCS计算；丁凡[14]基于射线追踪法(shooting and bouncing ray,SBR)对舰船的多次散射效应展开研究，分析了舰船目标的RCS计算方法；李敢等[15]提出了GPU-based SBR高频算法，满足舰船目标RCS的计算精度要求；陈世华等[16]分析粗糙海面的起伏特性、雷达入射电磁波对舰船RCS特性的影响。

随着电磁计算研究的不断进步，新的电磁仿真计算方法不断被提出，大致可分为时域法与频域法，其中频域法又分为低频方法与高频方法[17]。低频法包含矩量法(mothod of moments,MOM)、多层快速多极子(multi level fast multipole method,MLFMM)算法等；高频法包含几何光学法(geometric optics,GO)[18]、物理光学法(physical optics,PO)[19]、大面元物理光学法(large element physical optics,LE-PO)、射线跟踪-几何光学法(ray tracing geometric optics,RT-GO)等。

对于船舶这类复杂目标需要方便快捷、精度较高的计算方法，才能达到被测目标的理想电磁散射特性。文献[20]中提出传统的RWG(rao-wilton-glisson)基函数需要较小的网格单元(lam/6、lam/8、lam/10、lam/12)，改进的基函数方程LP-RWG(linearly-phased RWG)允许使用更大的网络元素(several λ)，从而提出了大面元物理光学法(large element-physics optics,LE-PO)，并在电大尺寸目标的电磁散射求解中取得了良好效果。

本文针对商船的适用性，对不同船舶的RCS展开了仿真分析，运用LE-PO算法探究了频率、入射角度、极化方式、不同船首向等对于整体RCS的影响，旨在得出不同船型在不同条件参数下的RCS计算结果，分析散射截面RCS的分布特点，为雷达目标识别提供参考。

1 电磁仿真求解技术

基于RWG基函数的PO算法采用三角面元模拟任意复杂目标的表面，并快速地计算目标表面电流，最终实现目标散射场的求解。基于PO算法求解目标面元网格需按照1/8λ进行划分，入射波波长λ=c/f,c为理想空间中的波速，f为入射波频率。典型普通的电小尺寸目标可快速实现散射特性的求解，然而，对于船舶、导弹、飞机3类目标电磁散射特性求解时，如果依照此网格划分标准，网格数量可达到上亿，对计算机硬件有着极大地挑战。

大面元物理光学法(LE-PO)[21]作为PO算法的改进算法，对RWG基函数的相位进行修正，使得PO算法对网格划分大小不再成为限定。采用LE-PO算法求解复杂电大尺寸目标散射问题，可采用与波长相当甚至几个波长的尺度进行剖分目标，较大程度上降低了目标的网格数量。与传统的物理光学法相比较，大面元物理光学法求解速度更快、需求资源更少，可实现超电大尺寸目标的RCS计算。

RWG基函数为：

(1)

大面元物理光学三角基函数公式[20]为：

(2)

式(2)中，当kn为0时，式(1)则转变成RWG基函数，并记为：fn(r)。

本文利用大面元物理光学法(LE-PO)电磁计算方法在超电大尺寸船舶目标下电磁求解。

2 船舶目标的特性分析与建模

为保证船舶模型的精确性，利用三维建模软件Catia创建船舶缩放模型，具体步骤如图1所示。

图1 创建船舶三维网格模型具体步骤Fig.1 Specific steps to create a 3D mesh model of a ship

表1 船舶参数设置Tab.1 Description of ship attributes

利用厦门港的某油轮和某散货船的真实船舶数据(如表1所示)，在Catia中形成船舶的三维几何模型，如图2所示。

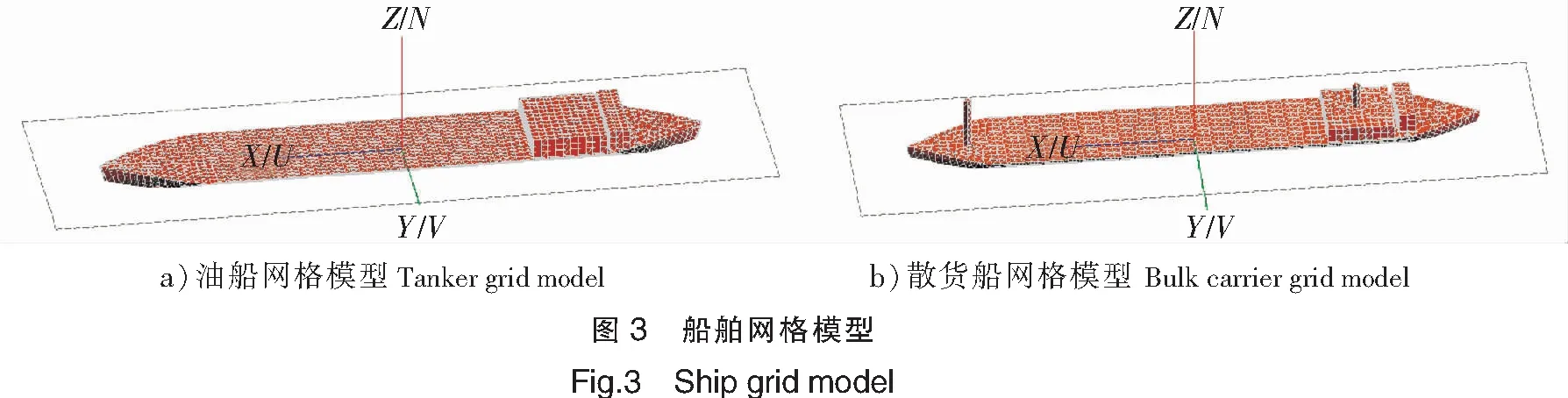
两种船舶网格模型如图3所示。

3 仿真分析

3.1 不同频率对单站RCS的影响

仿真设置：雷达入射波以Linear(线性极化方式)照射目标，选取两个频点，分别为f1=0.3 GHz、f2=30 GHz;入射角θ=90°;方位角φ=-180°～180°;两种船型满载且在垂直极化下，船首向未发生偏转，即船首向为0°。

对船舶单站RCS进行仿真，详细仿真结果如图4所示。

由图4a)可知，随着雷达波入射频率的升高，油船RCS波峰变化幅度较大，波谷的变动较小。入射频率为0.3 GHz时，RCS曲线的峰值在180 dB附近变化，此频率下的波长为1 m，船体的上层设备尺寸与波长相当，其上建筑结构多被雷达波检测。入射频率的升高，RCS曲线出现峰值升高、波谷的波动复杂度减少,频率为30 GHz时的波峰远高于0.3 GHz时波峰，波谷随入射波频率的提高复杂度较少。两种不同频率下，雷达波的峰值皆处于相同的φ角度，含5个波峰、4个波谷；随入射波频率的提高，波峰迅速增大，产生此种现象的原因是船体的侧壁、船首、船尾结构多为平面板或曲面板，使得产生的回波被直接反射。

由图4b)所示，入射波频率为0.3 GHz、30 GHz时，散货船波峰、波谷的数量远多于油船。当频率为0.3 GHz时，RCS曲线峰值在170 dB附近波动；当频率为30 GHz时，RCS曲线峰值位于210 dB上下，两种频率的RCS曲线波谷无明显差异。

3.2 不同极化方式对单站RCS的影响

按照极化方式，可分为线极化、圆极化、椭圆极化时，线极化Linear又细分为垂直极化、水平极化。本文分别在雷达波频率为0.3 GHz、30 GHz时，选择水平极化、垂直极化两种极化方式，对油船、散货船单站RCS进行仿真分析，其他仿真参数同上，仿真结果如图5、图6所示。

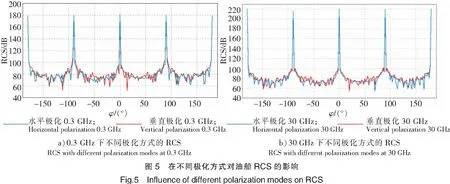
由图5可知，油船在0.3 GHz下水平极化的RCS与垂直极化的RCS在波峰处不相上下，而在波谷处，垂直极化比水平极化小得多且变化剧烈、复杂。然而在30 GHz时，两者极化方式在波峰处无明显区别，波谷处垂直极化仍小于水平极化的RCS，但差异程度变小了许多。随着频率的增大，两者的差异性有减少的趋势。已知0.3 GHz、30 GHz两个频率所对应的入射波长分别为1 m，0.01 m，由于1 m的波长与船舶上层结构尺寸相当，其结构的漫射效果减少，使得对应船体的反射信号功率增大，进一步加大了回波反射的强度。

由图6可知，RCS曲线较为直观地展示入射波频率为0.3 GHz、30 GHz时两者的波峰数量以及波峰大小，同一频率，水平极化、垂直极化的波峰数量及大小接近同步，垂直极化的波谷变化较为复杂、剧烈。

同一入射方向且同一频率的船舶目标，其散射强度由极化方式决定。

3.3 不同入射角对单站RCS的影响

入射波频率取30 GHz，线性极化方式选取垂直极化，方位角φ=-180°～180°，取2°为一个点，入射角θ分别设为45°和90°。船首向未发生偏转，即船首向为0°，两船在不同入射角下RCS的示意图如图7所示。

由图7可知，随着入射角的增大，对应方位角φ的后向RCS也相应增大。当油船俯仰角为45°时，后向RCS的最大值94.02 dB位于方位角φ=±90°处；当入射角为90°时，后向RCS的最大值219.29 dB位于方位角φ=±180°处。当散货船入射角为45°时，后向RCS的最大值95.7 dB位于方位角φ=±92.2°处；当入射角为90°时，后向RCS的最大值215.39 dB位于方位角φ=±180°处。随着入射角的增大，后向 RCS的最大值也逐渐增大。

3.4 不同船首向对单站RCS的影响

船舶在行驶过程中，时刻受到风流的影响[22]，在受限水域，风流对船舶航行、进出港、停靠等行为有着重大影响。

为了分析不同航向角，不同入射角下的RCS变化情况，本文分析了船舶左、右舷受风流影响情况，其中，船舶右舷受风流作用记为负方向，左舷受风流作用记为正方向。

仿真参数：入射波以Linear(线性极化方式)照射，入射频率取30 GHz；入射角设定为θ=45°、90°；方位角φ=-180°～180°，取2°为一个点；两种船型皆为满载，假定船首向(HDG)发生偏转，偏转角度分别为-10°、10°、-30°、30°。

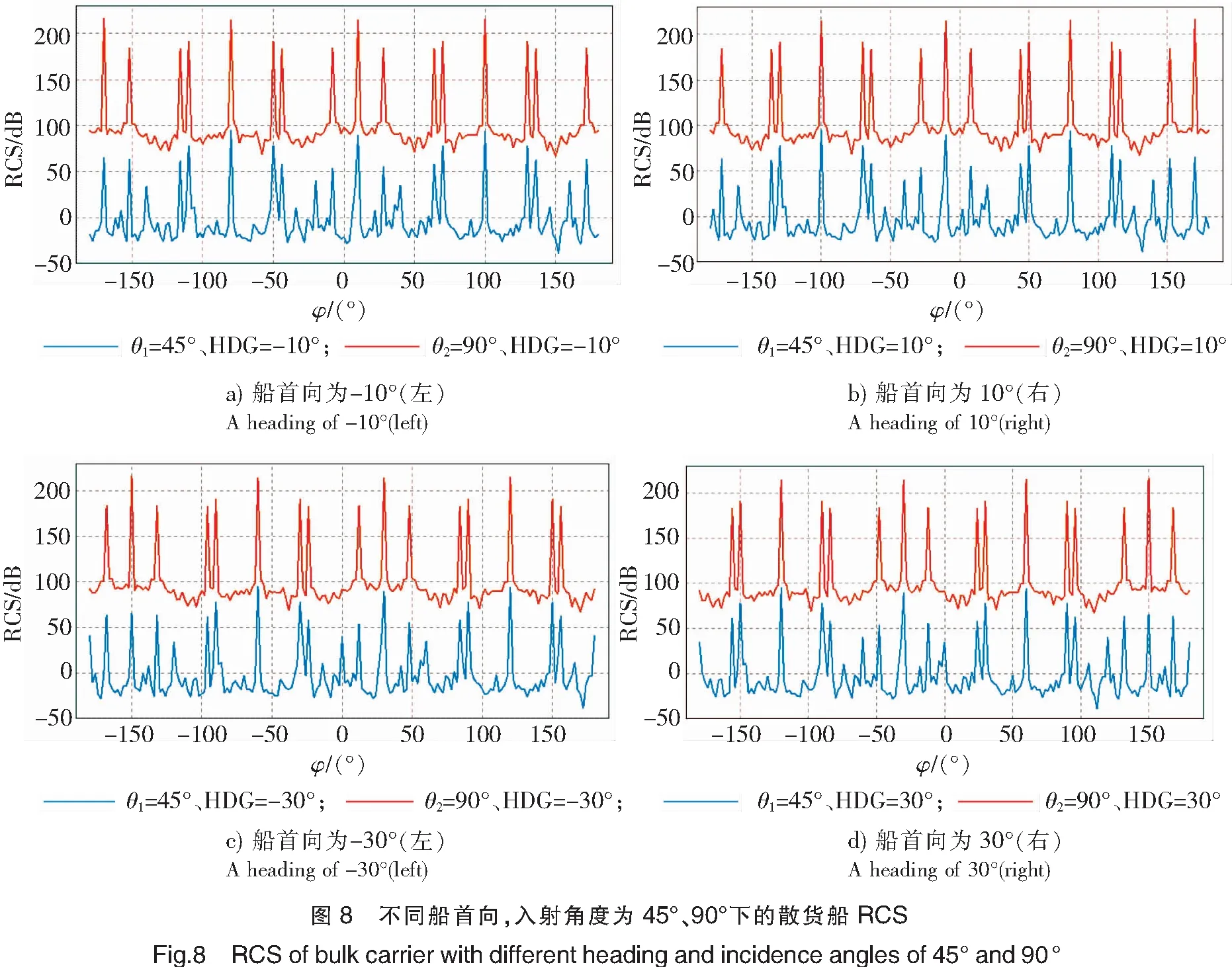
仿真结果如图8、图9所示。从图8、图9可：

1)在相同的仿真条件下，无论船首向角度为多大，该船舶RCS峰值并未发生变化。如：当入射角度为45°时，油船的RCS峰值为94.02 dB，散货船的RCS峰值为95.83 dB；当入射角为90°时，油船的RCS峰值为219.29 dB；散货船的RCS峰值为215.39 dB。

2)船舶航行时，受风流作用，船舶的船首向左、右发生一定的偏转，当雷达波入射角为90°时，RCS峰值仍保持方位角对称性；当雷达波入射角为45°时，RCS峰值不保持对称性；船舶的船首向发生偏转时，雷达波所照射的船体更宽，船体对雷达波的反射能力就越强。

4 结论

本文以油船、散货船为研究对象，利用Catia、Hyper mesh、FEKO创建船舶目标三维模型及网格模型，分别介绍了网格大小及数量，并以此为基础，分析了油船、散货船在不同雷达入射频率、不同极化方式、不同入射角度和不同船首向的单站RCS曲线变化。得出：两种船型在同种极化方式下，频率越高，雷达散射截面的贡献越大；同一入射频率，单站RCS的强度由极化方式决定；极化方式、入射频率一定时，船舶后向RCS随着俯仰角的增大而增大。油船、散货船RCS计算与分析是商船设计领域的重点工作，精确预估RCS，不仅可提高船舶设计水平，更能提高船舶航行的安全性。该研究为未来的船舶回波图像仿真提供理论基础，可以更精确高效地对船舶总体RCS的散射特性进行量化分析。