基于马尔科夫链-BP神经网络模型对公路运量的预测研究

裴同松，裴 彧

(1.河北交通职业技术学院 电气与信息工程系,河北 石家庄 050091；2.河北交通职业技术学院 土木工程系,河北 石家庄 050091)

0 引 言

随着社会的进步和国民经济的蓬勃发展，公路运输业也逐步走向繁荣。到目前为止，公路运输已经在国民经济中占据了举足轻重的地位。公路运输业的快速发展为人们创造便捷生活的同时也不可避免的产生交通堵塞或交通意外等问题。合理的预测出公路的运输量(客运量与货运量)一方面可以加强公路的基础设施建设，另一方面可以使交通管理部门对公路运输进行统筹规划，为交管部门制定交通生产、组织、运输计划夯实基础。因此如何快速准确的预测公路运量将对解决相应的公路运输问题提供极大的帮助。

国内外的学者对事物的预测方法主要有：统计回归法[1]、时间序列法[2]、逆阵求解法[3]、灰色预测法[4]、神经网络法[5]、马尔科夫链[6]等。例如申嘉荣等[7]利用神经网络对碾压混凝土坝层面抗剪断强度进行了预测；郑峰等[8]利用马尔可夫链合理的预测了未来人才流动方式；柯福阳等[9]利用BP神经网络对精确的预测分析了滑坡地质灾害。

考虑到公路运输量变化具有随机性、变化条件复杂性以及变化波动大等因素，因此笔者在前人研究的基础上将新陈代谢法与BP神经网络模型结合并使用马尔科夫链对新生成的预测模型进行相对值修正，最终达到提高预测精度的目的。

1 预测模型

1.1 BP神经网络

神经网络系统目前已经成为人工智能领域中的重要一环，并且发展了包括多层感知器、Kohomen自组织特性映射、Hopfield网络、BP网络、RBF网络等在内的数十种网络。其中，采用反向传播算法的BP网络应用最为广泛。BP神经网络信息传递方式与人体神经元传递方式大体相同，它由输入层、隐含层、输出层组成，输出函数一般是logsig函数、tansig函数以及purelin函数[10]。通用神经元模型及BP神经网络结构如图1和图2。

图1 通用神经元模型

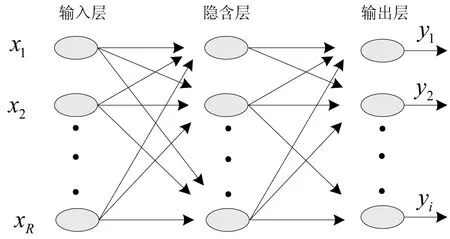
图2 BP经网络结构

图1和图2中x1,x2…xR为输入向量、wi,1为向量权重、bi为阈值、y1,y2…yR为输出向量。

由于BP神经网络是由多个神经元共同传递信号输出，因此第n个神经元的输出向量为：

(1)

第i个经过传递函数输出的神经元表达式为：

yi=f(n)=tansig(ni)

(2)

新陈代谢法修正BP神经网络具体建模过程如下：

1)将原始数据进行归一化处理并作为BP神经网络中的输入向量，以实际值作为网络模型的训练目标对BP神经网络进行训练。

2)通过使用新陈代谢法不断更新BP网络训练后的起始数据与末尾数据从而使样本序列始终保持更新状态。

3)将预测得到的拟合值作为输出目标值，如果输出向量不满足期望值立即进行逆方向传播训练直至得出期望的仿真结果。

BP神经网络具体运算过程如图3。

图3 组合模型流程

1.2 马尔科夫链修正模型

马尔科夫链属于随机过程理论中的典型代表，它依靠使用当前系统的状态通过求解状态转移矩阵推断下一次等时距的系统所处状态。马尔科夫链适用于随机性大、数据波动明显的随机系统[11]，通过马尔科夫链对数据的修正，可以使原系统所得结果更加精确。马尔科夫链在文中具体应用过程如下：

1)根据BP神经网络预测出的期望值与实际值进行相对值计算，可以将相对值合理的分成若干个状态区间。状态区间为：

Ei=[Qi1,Qi2] (i=1,2,…,k)

(3)

式中：Qi1,Qi2分别为状态区间的上限和下限。

2)将状态Ei通过k步转移到状态Ej出现的次数为Mij，Mi为状态Ei出现的次数，则Pij为状态Ei到状态Ej的一步转移概率，如式(4)：

(4)

式中：

(5)

3)假设将最初的状态向量定义为S(0)，那么转移K步之后得到向量将定义为：

S(k)=S(0)×P(k)

(6)

(7)

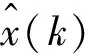
1.3 模型精度检验

(8)

2)后验差C:

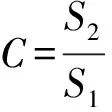
(9)

3)小概率误差P：

(10)

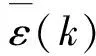
表1 预测模型精度等级划分标准

2 实例分析

选取河北省某地区1998—2017年的公路客运量和公路货运量作为样本数据。

（3）降水对空气质量有一定的影响，降水量多的时候，空气中污染物的质量浓度较小，这是由于降水加速了空气中污染物扩散，空气质量较为优良。而在无降水天气，污染物容易堆积，空气质量较差。因此，在空气污染较为严重的天气，可以通过增大降水量来改善空气的质量。

2.1 应用BP神经网络预测

使用MATLAB2016a软件建立网络模型，为了保证神经网络模型的精度以及计算工作量，模型结构选取为3-7-2，使用tansig传递函数建立网络并使用traingdx函数作为网络训练函数，设置学习速率基值以及训练精度分别是0.05和0.001，训练步数最大值为30 000。将1998—2009年的运量数据为模型实际输入值，通过预测计算得出2010—2017年公路运量数据并分析对比。该地区具体运量数据见表2。

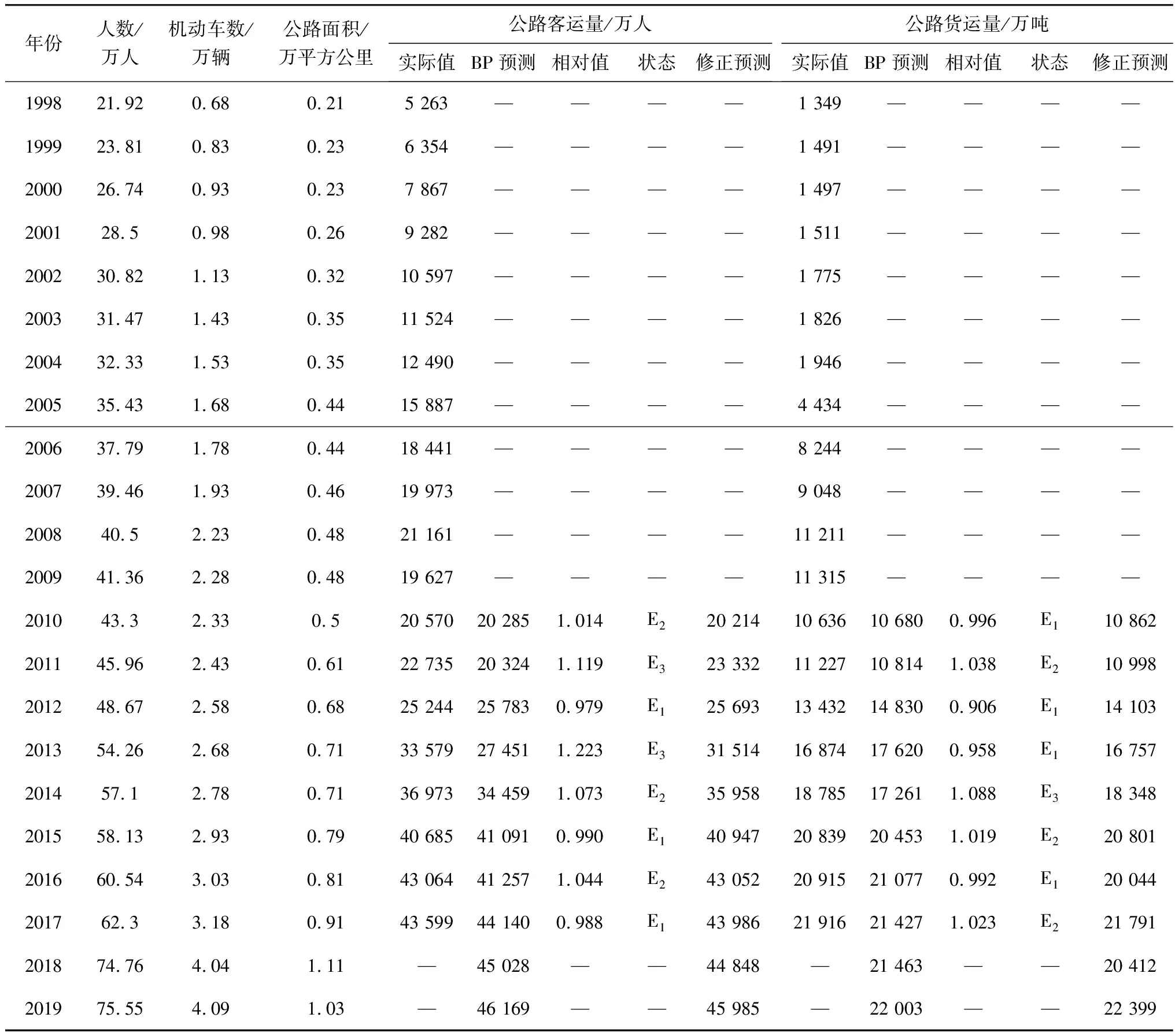
表2 河北省某地区公路运量统计

通过表1和表2计算可知，使用新陈代谢法优化的BP网络预测模型针对公路客运量的平均相对误差为5.70%，后验差为0.246，小概率误差为0.943；公路货运量的平均相对误差为3.99%，后验差为0.194，小概率误差为0.961，模型精度见表3。

表3 模型精度比较

由表3可知BP网络预测虽然较为准确但为了使预测模型进一步精确，笔者引入马尔科夫链对BP网络进行优化。

2.2 应用马尔科夫链优化BP网络

2.2.1 划分状态

根据表2公路运量的相对值依次将公路客运量划分为E1[0.979～1.013]、E2[1.014～1.03、E3[1.073～1.223]；公路货运量划分为E1[0.906～0.996]、E2[0.997～1.038)、E3[1.039～1.088]3种状态，公路运量状态划分见表2。

2.2.2 计算状态转移矩阵

1)公路客运量

由式(6)可知公路客运量经过一次状态转移矩阵后，得S(1)=(0.375 0,0.312 5,0.312 5)；经过两次状态转移矩阵得S(2)=(0.364 6,0.343 8,0.291 7)。因此公路客运量在2018年及2019年处于E1状态的概率最大。

2)公路货运量

由表2可知E1状态出现4次，E2状态出现3次，E3状态出现1次。初始状态向量为S′(0)=(0.500 0,0.375 0,0.125 0)。按式(4)并借助MATLAB2016a软件计算得如下状态转移矩阵：

由式(6)可知公路货运量经过一次状态转移矩阵后，得S′(1)=(0.385 0,0.365 0,0.250 0)；经过两次状态转移矩阵得S′(2)=(0.343 7,0.437 5,0.218 7)。因此公路货运量在2018年及2019年分别处于为E1状态和E2状态的概率最大。

2.2.3 马尔科夫链修正预测值

根据2010—2017年公路运量所处的状态，参照式(7)计算可得马尔科夫链修正后的BP神经网络预测值，修正值见表2。

2.3 修正后模型精度检验

参照表2计算可知，使用马尔科夫链修正后的BP网络预测模型针对公路客运量的平均相对误差为2.07%，后验差为0.098，小概率误差为0.979；公路货运量的平均相对误差为2.14%，后验差为0.099，小概率误差为0.979。

2.4 模型分析对比

2.4.1 马尔科夫链修正模型与原BP神经网络预测模型对比

通过使用马尔科夫链修正BP神经网络预测值，发现在公路客运量上马尔科夫链修正值将平均相对误差下降2.63%，在公路货运量的预测中也将平均相对误差下降1.85%，预测模型的各个指标均达到了一级精度，在一定程度上提高了预测模型的精度，使得模型预测值与实际值拟合更加准确。在模型对比图中也可以清楚的观察到修正值是一条与实际值拟合更准确的曲线，弥补了BP神经网络模型偶尔模拟失真的缺点，即使用马尔科夫链修正BP神经网络模型可以应用到实例预测与分析。具体精度对比数据见表3，模型对比图见图4及图5。

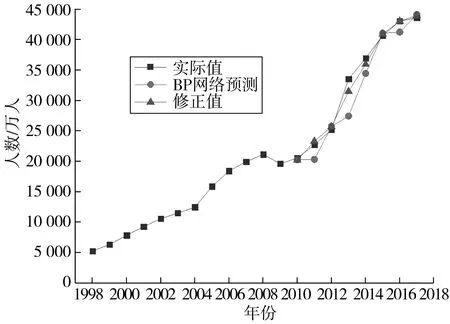
图4 公路客运量模型对比

图5 公路货运量模型对比

2.4.2 马尔科夫修正模型与高阶方程修正模型对比

为了便于修正模型之间的对比，现引入高阶方程拟合模型修正BP神经网络。

1)针对BP神经网络公路客运量数据得出数学模型为:

y1=16.308x5-360.32x4+2 758.8x3-8 396x2+

12 033x+14 035(x=1,2…,n)

2)针对BP神经网络公路货运量数据得出数学模型为：

y2=-140.56x2+2 968.1x+6 998.3(x=1,2…,n)

式中：y1和y2分别为高阶方程修正值，设定2010年为x=1并以此类推。

通过高阶方程拟合2010—2017年公路运量的数据可得公路客运量的平均相对误差为4.90%，后验差为0.161，小概率误差为0.951；公路货运量的平均相对误差为4.61%，后验差为0.184，小概率误差为0.954，参照表1可知，模型精度为二级。马尔科夫链修正的BP神经网络模型与高阶方程修正的BP神经网络模型对比图见图6及图7。

图6 公路客运量模型对比

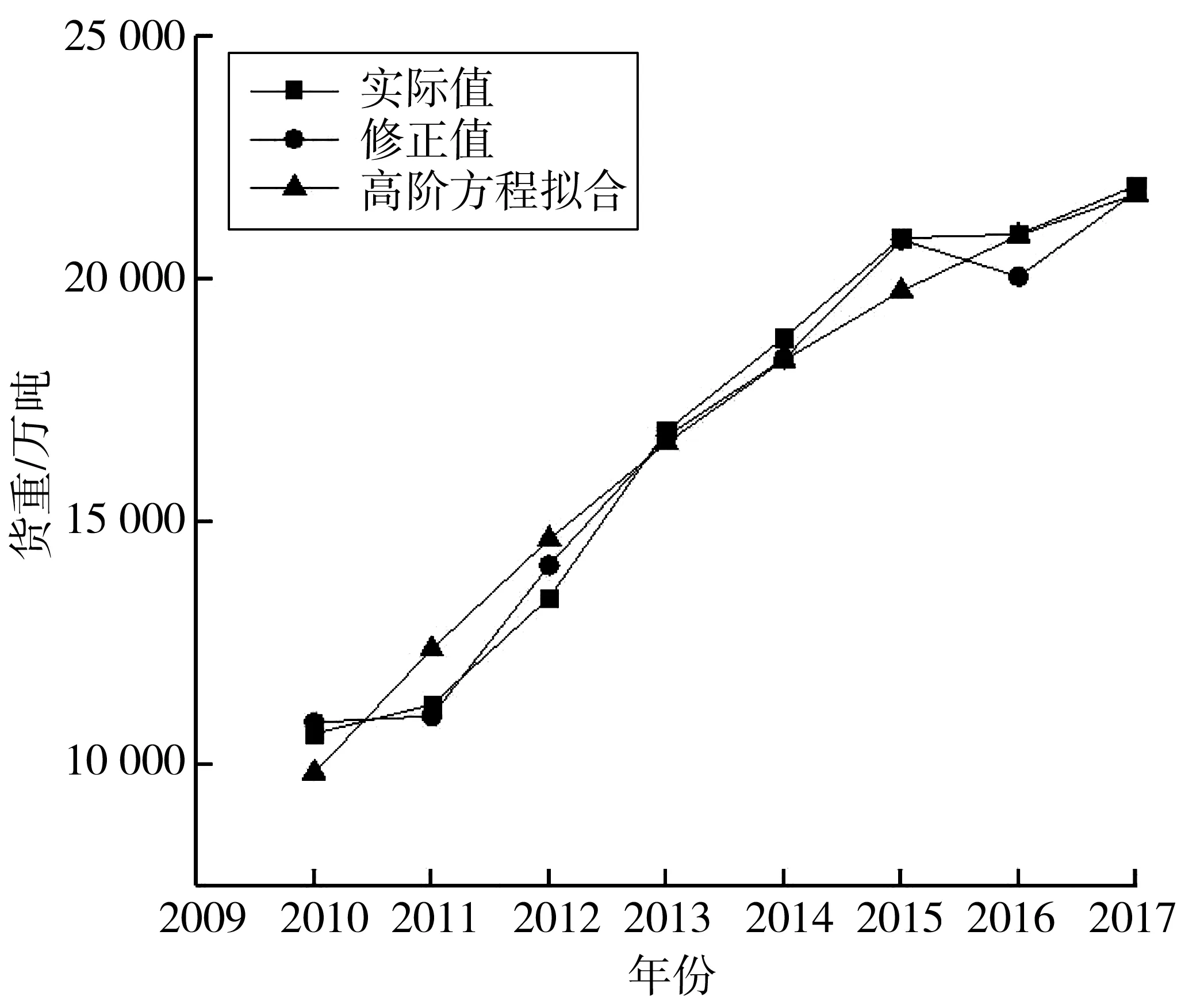
图7 公路货运量模型对比

根据模型之间的对比分析可知，马尔科夫链修正后的BP神经网络模型平均相对误差更小，精度更高；从对比图也可以看出马尔科夫链修正的神经网络模型更加切合实际值曲线。因此，相较于高阶方程拟合后的BP神经网络模型，马尔科夫链修正模型更适合应用于公路运量的预测。

2.5 实例预测

引入表2中2018年及2019年公路运量的人数参数、机动车数参数、公路面积参数到上文中的BP神经网络中，借用Matlab2016a软件设置学习速率基值以及训练精度分别是0.05和0.001，训练步数最大值为30 000，可得2年的公路运量预测值，见表2。

由于上文已使用状态转移矩阵计算出2018年与2019年公路客运量状态均是E1状态，公路货运量分别是E1与E2状态。由式(7)计算可得2018年的公路客运量与货运量分别是44 848万人和20 412万吨；2019年的公路客运量与货运量分别是45 985万人和22 399万吨，马尔科夫链修正值见表2。

3 结 语

使用马尔科夫链修正的BP神经网络模型可以将模型精度的各个指标均提高至一级精度，并且可以将公路运量的平均相对误差缩小到2.07%和2.14%。

使用修正后的BP神经网络预测出2018年及2019年公路运量。即2018年的公路客运量与货运量分别是44 848万人和20 412万吨；2019年的公路客运量与货运量分别是45 985万人和22 399万吨。

使用马尔科夫链修正后的BP神经网络预测未来公路运量可以很好的把握未来公路运输发展趋势，同时也可以为公路运输发展决策者提供有利信息。