基于时序分析的锈蚀RC拱损伤识别:仿真与验证
2021-03-05唐启智辛景舟周建庭
唐启智,辛景舟,2,周建庭,付 雷,3,张 俊
(1.重庆交通大学 土木工程学院,重庆 400074; 2.广西交通投资集团有限公司,广西 南宁 530022; 3.贵州桥梁建设集团有限责任公司,贵州 贵阳 550000; 4.贵州毕节高速发展有限公司,贵州 毕节 551700)
0 引 言
拱桥因其结构形式多样、造型美观、刚度大等特点,在我国公路、铁路系统中得到广泛应用[1]。随着服役年限的增加,拱桥性能劣化在所难免,识别拱桥的损伤状态,掌握其运营状况,对于保障国家、社会与人民群众的生命财产安全,具有重要的科学研究意义与工程实用价值[2]。
国内外学者针对拱桥的损伤识别开展了大量的研究。B.ALEMDAR等[3]通过运营模态分析对圬工拱桥的固有频率和阻尼比进行了研究;D.CAPECCHI等[4]提出基于模态频率、振型与曲率的损伤识别方法,并在抛物线拱上进行了试验验证;M.M.ALAMDAN等[5]提出了基于谱矩的方法,以识别澳大利亚悉尼海港大桥子结构中可能存在的结构损伤或异常;周宇等[6]提出柔度曲率梯度的损伤特征指标并应用于刚架拱桥损伤识别;项贻强等[7]通过对钢管混凝土中承式拱桥吊杆加速度响应信号进行离散小波变换,提出基于小波总能量相对变化的损伤识别方法;姜绍飞等[8]提出一种基于模态指标和数据融合的结构损伤识别方法,应用该法定位了钢管混凝土拱桥的损伤。可见,目前拱桥的损伤识别主要集中在频域方法且相关研究较少。
时间序列分析是最具代表性的时域方法[9],由于其理论基础成熟、无需进行繁琐的频谱分析,已逐渐成为损伤识别领域的热点。国内外学者对基于时间序列的结构损伤识别进行了大量的研究。M.KRISHNAN等[10]提出了一种基于时变自回归模型和主成分分析的损伤识别方法,实现了多自由度振动结构连续损伤在线检测;D.ALESSIO等[11]对自回归模型和马氏距离平方法在结构健康监测领域的应用进行了全面的敏感性分析;H.SIMON等[12]使用遗传算法对自回归模型系数进行了优化选择,构造了敏感性指标,实现了风力发电机叶片早期损伤的识别;杜永峰等[13]利用自回归模型残差的方差与待识别工况残差的方差之比作为损伤指标,通过数值模拟的方法对一简支梁进行损伤识别研究;刘纲等[14]基于向量自回归模型,以模型系数的对角线元素的马氏距离构造损伤指标,进行了损伤定位和程度的识别。由此可见,时间序列分析在结构损伤识别领域已取得长足发展,但研究对象仅仅是一些简单的构件,如简支梁等。
基于拱桥损伤识别的复杂性与既有方法的不足,笔者开展了基于时间序列的RC拱桥损伤识别研究。首先,介绍了时间序列模型的建模方法,将待识别工况与完好工况的模型残差的方差之比作为损伤特征指标;其次,构建了钢筋锈蚀与结构刚度退化的关系,建立了试验拱肋的数值模型,利用静力试验数据对数值模型进行验证之后,得到了不同损伤工况下的加速度响应;然后,对不同损伤工况下的响应数据建立时间序列模型,并提取损伤特征指标,获取了锈蚀率与损伤特征指标之间的定量关系,提出了针对不同钢筋直径的识别模型;最后,将试验数据送入所提识别模型进行预测,验证了所提方法。图1是全文的具体框架,图中直接从锈蚀与刚度退化关系的建立开始,时间序列模型的建模方法会在第1节介绍。
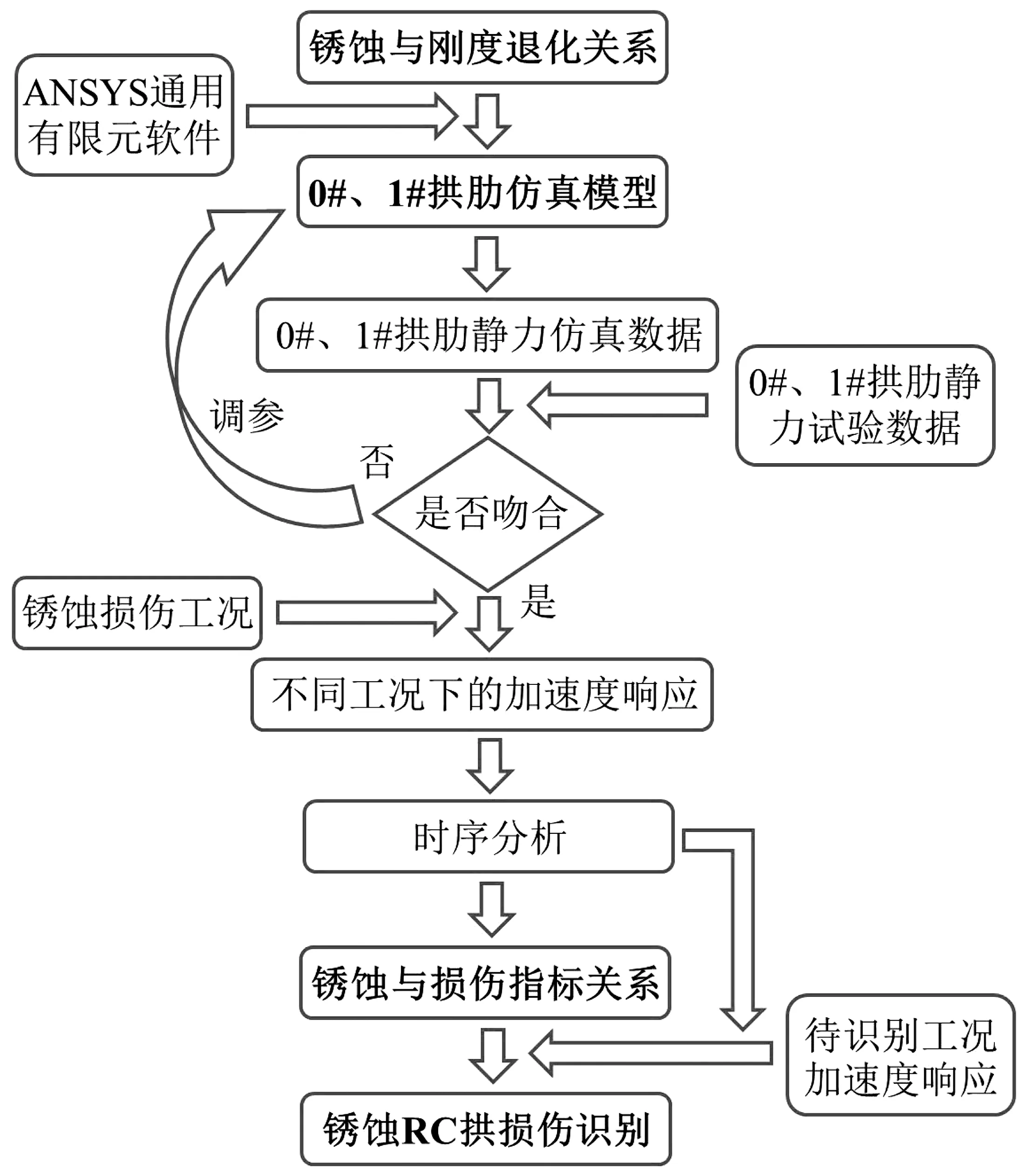
图1 全文框架
1 时序分析方法
1.1 时间序列模型
根据数据的平稳性,时间序列模型可以分为非平稳时间序列模型和平稳时间序列模型[15]。非平稳时间序列模型包括确定性趋势、随机性趋势模型,由于其数据相关性不高,预测结果可靠性不强,一般可通过差分或消除趋势来使其平稳化。平稳时间序列模型根据残差项是否存在异方差性,可分为:线性时间序列模型,包括自回归(AR)模型、滑动平均(MA)模型、自回归滑动平均(ARMA)模型等;非线性时间序列模型,包括自回归条件异方差(ARCH)模型、广义自回归条件异方差(GARCH)模型等。实际应用过程中,根据数据特点建立相应的时间序列模型即可。
如果一个随机变量序列中的观测量at可以表示为:
(1)
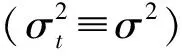
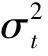
(2)
式中:c为常数;βi≥0,i=1,2,…,p;αj≥0,j=1,2,…,q分别为方差项和残差项的系数。
ARCH(q)模型是GARCH模型在p=0时的一个特例,两者可以认为是在ARMA模型的基础上,对残差项进行建模、修正的过程。
1.2 时序模型建模方法
由于平稳时间序列模型在实际应用中更为广泛,这里主要介绍平稳时间序列模型的建模流程:
1)数据平稳性检验。平稳性检验即单位根检验,笔者采用ADF(augmented dickey-fuller)法进行平稳性检验。ADF检验有3个检验模型为:
(3)
模型中α、β、δ为回归系数,原假设H0为3个模型中至少存在一个单位根(δ=0),备选假设H1为序列不存在单位根。实际检验过程中从模型3至模型1依次检验,若拒绝H0,则认为序列不存在单位根,即序列平稳。若序列非平稳,可以通过差分等方式使数据平稳化。
2)模型识别,即判断采用何种时间序列模型,一般运用序列的自相关函数(ACF)和偏自相关函数(PACF)图,根据各个时间序列模型的截尾和拖尾特征来进行判别:MA模型表现为自相关函数截尾,偏自相关函数拖尾。AR模型表现为自相关函数拖尾,偏自相关函数截尾。ARMA模型表现为自相关函数拖尾,偏自相关函数拖尾。
3)模型定阶,即确定模型滞后的阶数。笔者采用AIC(Akaike’s information criterion)准则,选取使得该准则值较小的阶数作为模型阶数。
4)参数估计。模型参数估计的方法有矩估计、最大似然估计和最小二乘估计。笔者采用最小二乘估计,其基本思想是对于一般的ARMA(p,q)模型,寻找使得残差平方和最小的一组参数值,即:
(4)
式中:s=max{p,q}+1。
5)模型检验。当参数估计完后,需要检验模型是否充分描述了数据,主要检验残差是否存在异方差性。笔者采用ARCH LM检验法进行残差异方差性检验,其基本思想是对时序模型残差的平方运行如下的回归:
(5)
ARCH LM检验的H0为残差中直到p阶都没有异方差效应,H1为残差存在p阶异方差效应。当检验统计量小于假定显著性水平的临界值时则拒绝H0。
若残差存在异方差性,即接受H1,高阶时需要建立GARCH模型,低阶时则建立ARCH模型来对残差项进行修正。
时间序列模型建模流程如图2。建立好时间序列模型后,构造损伤特征指标,通过特征指标与结构损伤间相联关系的建立,实现结构的损伤诊断。
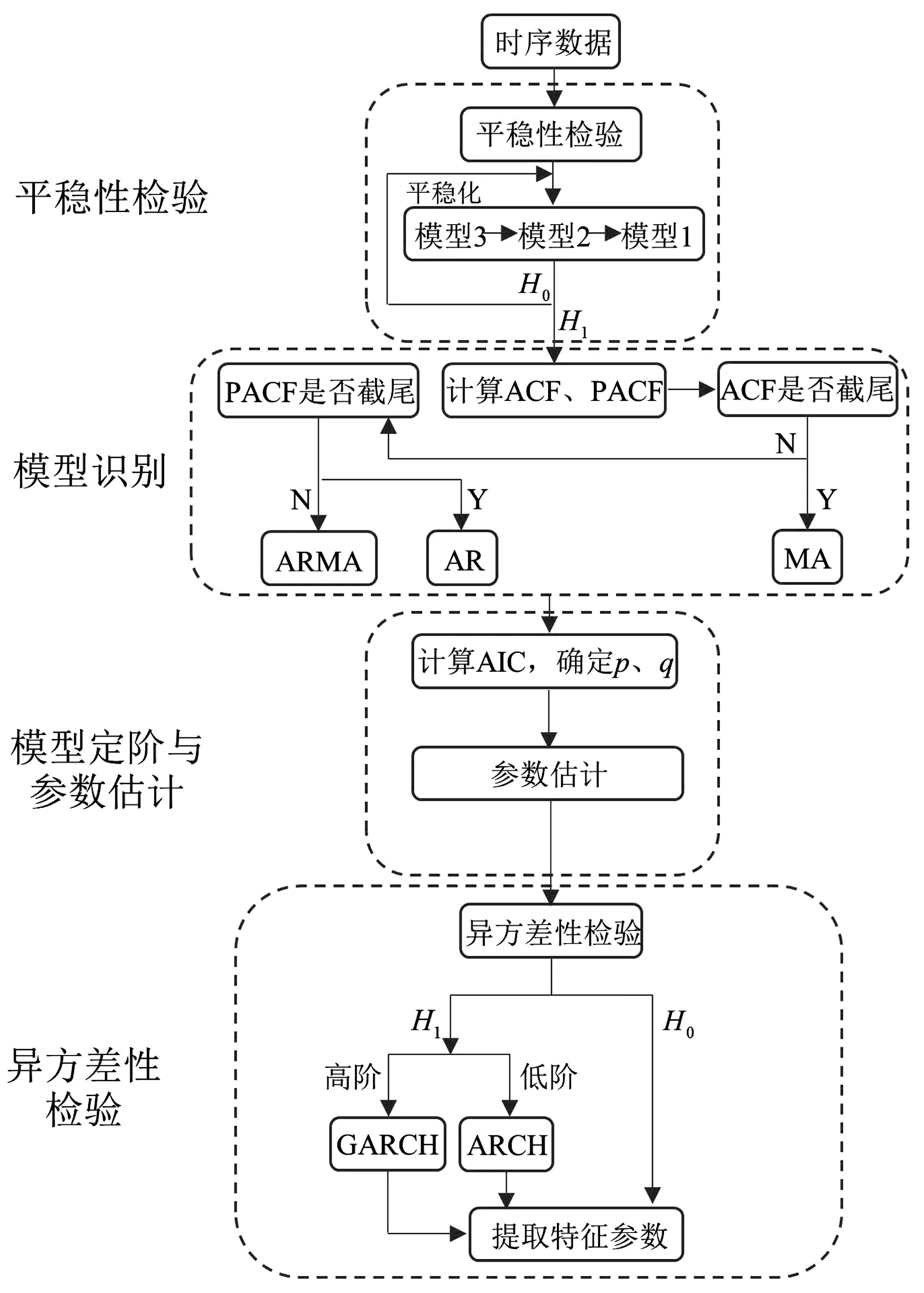
图2 基于时间序列模型的损伤特征提取
1.3 损伤特征指标建立
综合已有研究成果,发现国内外学者建立了各种各样的损伤特征指标,大致包括基于残差方差的损伤特征指标、基于自回归系数的损伤特征指标等。文献[13]采用基于残差方差的损伤指标,取得了一定的效果,于是笔者采用基于残差方差(这里指的是样本方差,有别于前文所述残差总体方差)的损伤特征指标。
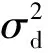
(6)
2 模型试验与数值仿真
2.1 模型试验概况
模型试验采用的是钢筋混凝土矩形肋拱,为模拟结构真实的应力水平,根据相似理论,在拱肋相应位置施加配重,模型拱基本参数与测点布置如图3。
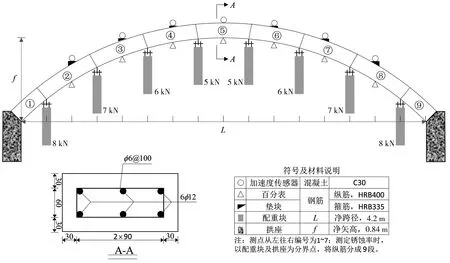
图3 模型拱基本参数
模型试验共制作了两片拱,一片未锈蚀,另一片锈蚀,分别记为0#、1#拱。采用通电加速锈蚀的方法对模型拱进行锈蚀,按10%的锈蚀率设定锈蚀时间,待达到预定时间之后,终止锈蚀过程。
动力试验时,使用橡胶锤自由下落,在拱顶施加冲击激励,并采集加速度响应信号。静力试验时,使用油压千斤顶,在拱肋3L/4(测点6)处按力加载的方式,加载至拱肋破坏。试验过程中获取了0#拱完好状态、加载破坏和1#拱锈蚀损伤、加载破坏4种工况的加速度响应数据以及0#、1#拱加载破坏全过程的静力数据,试验过程见图4。

图4 试验过程
试验完成后,对1#拱破拆,分9段(图3注释)称量钢筋锈蚀后的重量,按式(7)计算各段的锈蚀率,各节段实际锈蚀率见表1。
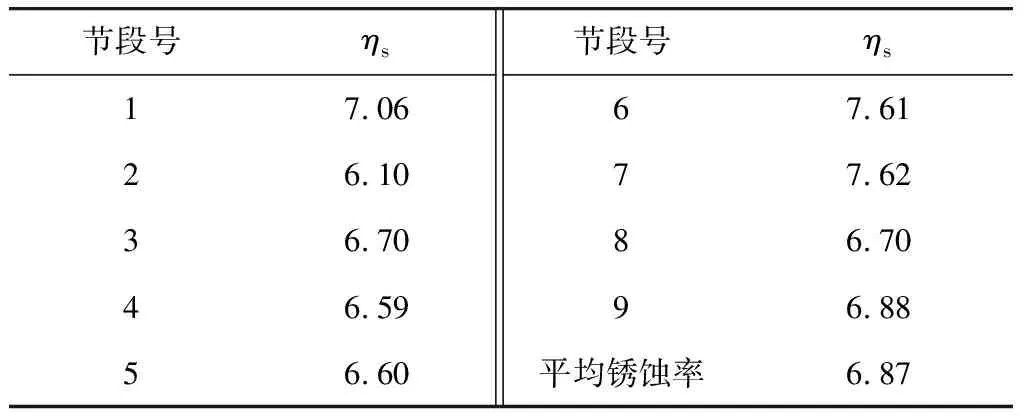
表1 实际锈蚀率
(7)
式中:m、mc分别为锈蚀前后钢筋的实际重量。
由于仅进行了1#拱的锈蚀试验,未能获取不同锈蚀程度下的加速度响应数据。为了获取更多的损伤工况,以建立锈蚀与损伤特征指标之间的映射关系,故采用数值仿真获取结构在不同锈蚀率下的响应数据,并与实测静力数据对比来验证数值仿真结果的正确性。
钢筋锈蚀引起的锈胀裂缝是导致结构刚度退化的主要成因,从而造成动力响应的变化。然而在有限元模型中模拟大范围的锈胀裂缝是较困难的,因此2.2节先给出锈蚀与刚度退化之间的定量关系,然后在2.3节进行有限元模型的建立。
2.2 锈蚀与刚度退化的关系
钢筋锈蚀对截面刚度的影响主要从以下3个方面得以体现[16]:①钢筋锈蚀会引起钢筋自身截面的减少,从而影响钢筋的力学性能;②钢筋锈蚀产生的锈胀产物会在约束混凝土作用下形成锈胀力,使混凝土产生软化效应,进而产生锈胀裂缝;③钢筋锈蚀会降低钢筋与混凝土之间的黏结作用。
需要指出的是,笔者仅考虑锈蚀作用下导致的截面刚度退化。
钢筋锈蚀后,其屈服强度、弹性模量都会有所下降,梁岩等[17]给出了钢筋锈蚀后材料性能计算公式为:
fyc=(1-1.727ηs)fy
(8)
Esc=(1-1.018ηs)Es
(9)
式中:fyc、Esc分别为锈蚀后的屈服强度和弹性模量;fy、Es分别为未锈蚀的屈服强度和弹性模量;ηs为钢筋锈蚀率。
钢筋锈蚀后,其截面半径将减小,笔者采用均匀锈蚀下的理论计算公式[18]为:
(10)
则钢筋锈蚀深度为:
(11)
式中:r为未锈蚀情况下的钢筋半径。
由于钢筋锈蚀后锈胀力的作用,混凝土性能也将有所改变,笔者采用文献[19]所提出的钢筋锈蚀后混凝土性能计算公式为:
f′cu,k=(0.704 9+0.295 1e-4.131 7ηs)fcu,k
(12)
(13)
式中:f′cu,k为锈蚀后混凝土立方体抗压强度;fcu,k为混凝土立方体抗压强度;Ecc为锈蚀后混凝土弹性模量。
截面刚度按GB50010—2010《混凝土结构设计规范》所推荐的公式进行计算,并引入考虑钢筋与混凝土黏结性能退化的刚度退化系数:
(14)
式中:B为截面刚度;β为考虑黏结退化而引入的刚度退化系数;其余符号与GB50010—2010《混凝土结构设计规范》中相同;对于锈蚀后的钢筋,钢筋截面尺寸、材料性能等取锈蚀后实际值。
β取值按孙彬等[20]通过试验研究所提出的计算公式为:
(15)
式中:x为钢筋锈蚀深度,按式(11)计算。
2.3 有限元模型建立
依据上述定量关系,笔者采用ANSYS建立了0#与1#拱的有限元模型,以弹性模量的折减来模拟截面刚度的退化,混凝土采用SOLID65单元,钢筋采用LINK8单元,加载块采用SOLID45单元,共划分为2 888个单元,如图5。混凝土的本构关系采用多线性等向强化模型(MISO),并关闭压碎,且考虑拉应力释放,钢筋的本构关系采用双线性等向强化模型(BISO)。材料应力-应变关系的输入采用GB50010—2010《混凝土结构设计规范》所推荐的公式,应力-应变关系曲线如图6。

图5 有限元模型
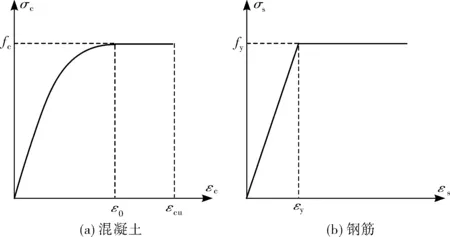
图6 材料应力-应变关系
边界条件以面约束的形式施加,约束两拱脚所有平动及转动位移;配重通过加载块的自重来施加,并根据力值大小及加载块体积换算等效密度。
静力分析中加载位置与模型试验一致,并以面荷载的形式施加。求解时,按力加载,并打开自动时间步和位移收敛准则,且将收敛条件放宽至5%。0#、1#拱极限荷载的有限元计算结果分别为64.2、58.1 kN,与试验值61、55 kN相差5.2%和5.6%。图7是0#和1#拱在3L/4截面的荷载-位移曲线仿真与试验值的对比。从图7中可以看出,有限元模型和实测结果吻合程度较高,即说明笔者所建立的有限元模型以及锈蚀率-刚度退化关系是合理的。
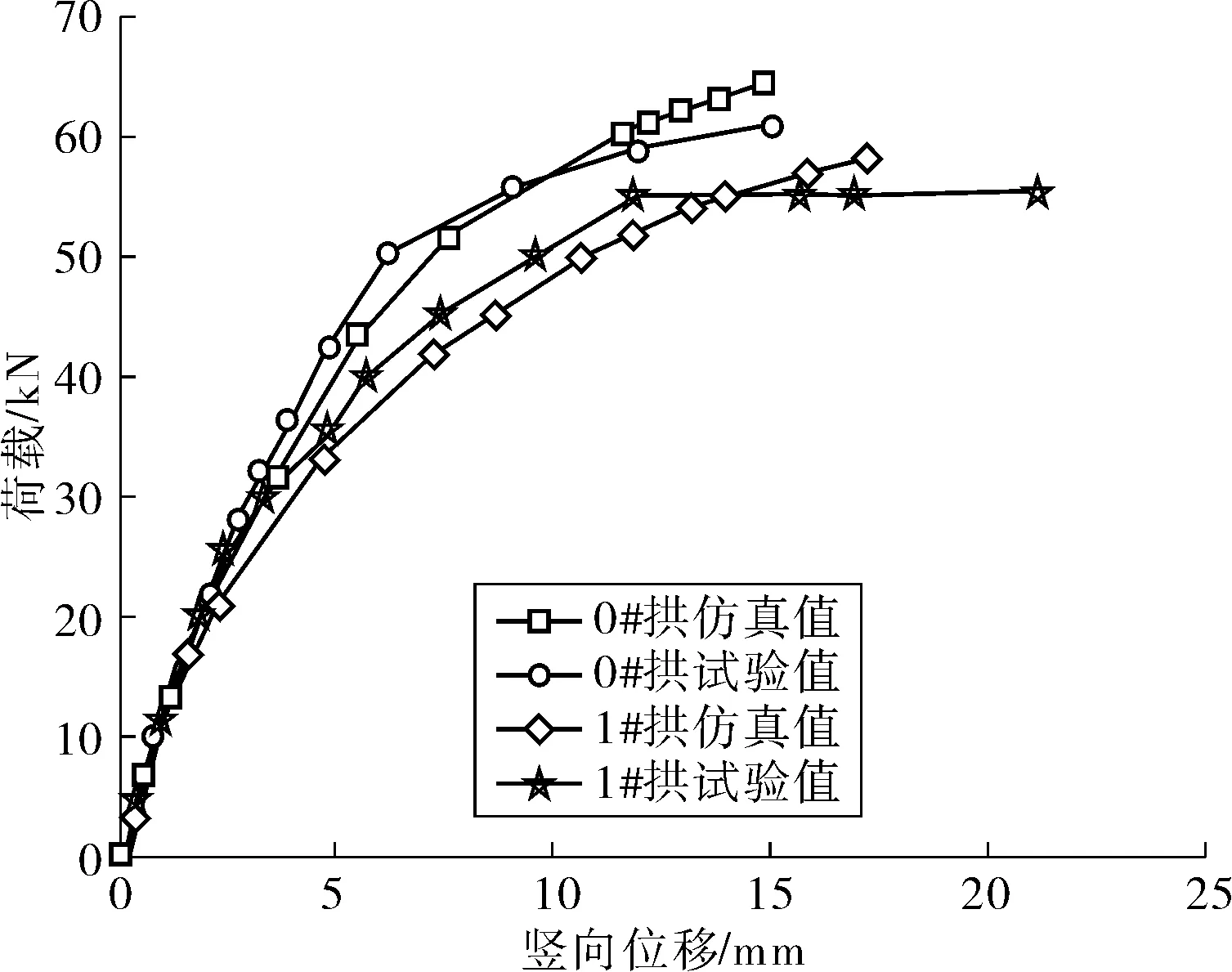
图7 荷载-位移曲线对比
2.4 工况划分及损伤识别模型建立
进一步地,为建立锈蚀与损伤特征指标之间的关系,在有限元模型中模拟了多种损伤工况,损伤为结构整体损伤,具体划分情况见表2。在拱顶施加白噪声激励,获取模型拱在不同损伤程度(锈蚀率)下的加速度时程响应数据。
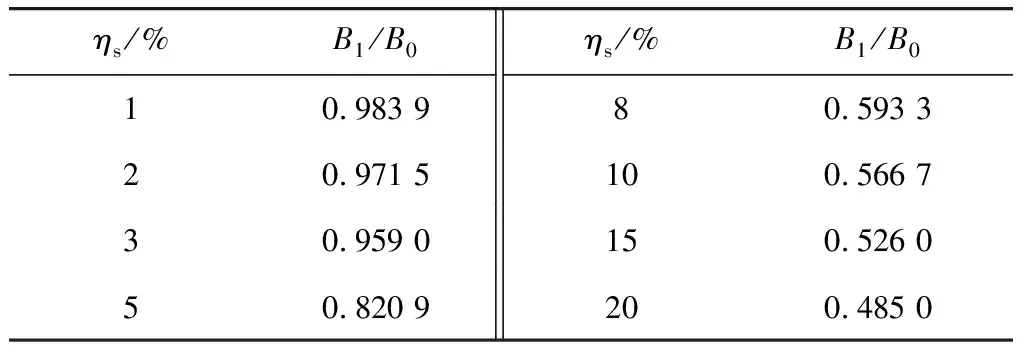
表2 损伤工况划分
获取不同损伤工况下的加速度响应后,基于Matlab软件平台,编程建立了完好状态下的时间序列基准模型,其余工况按此基准模型建立。以完好状态下测点2的加速度响应数据为例,简要介绍时序模型的建模过程:
1)平稳性检验。对样本数据进行单位根检验,模型3、模型2、模型1的统计量都为-28.91,远小于各自所对应的95%显著性水平的临界值-3.41、-2.86、-1.94,于是接受H1,即该数据序列不存在单位根,可进行平稳时间序列建模。
2)模型识别。由图8可知,ACF拖尾,PACF截尾,故应采用AR模型。
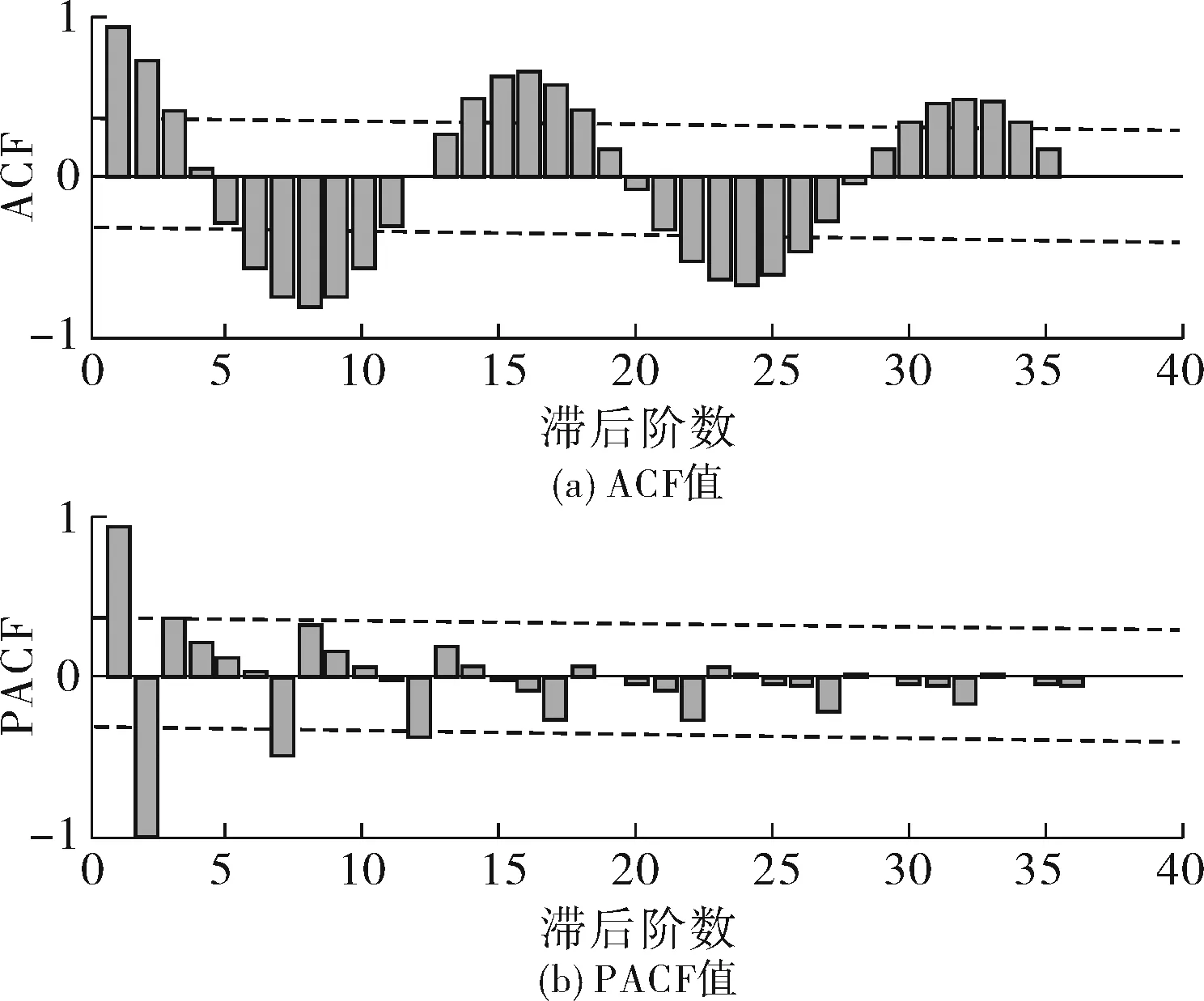
图8 ACF与PACF变化
3)模型定阶。回归不同滞后阶数的AR模型,提取各模型的AIC值等。由图9看出,模型的AIC值在滞后3阶后逐渐趋于稳定,且拟合优度R2>0.99。综合各节点响应数据的AIC值、系数显著不为零以及滞后阶数不宜过多的原则,选取AR(4)作为基准时间序列模型。
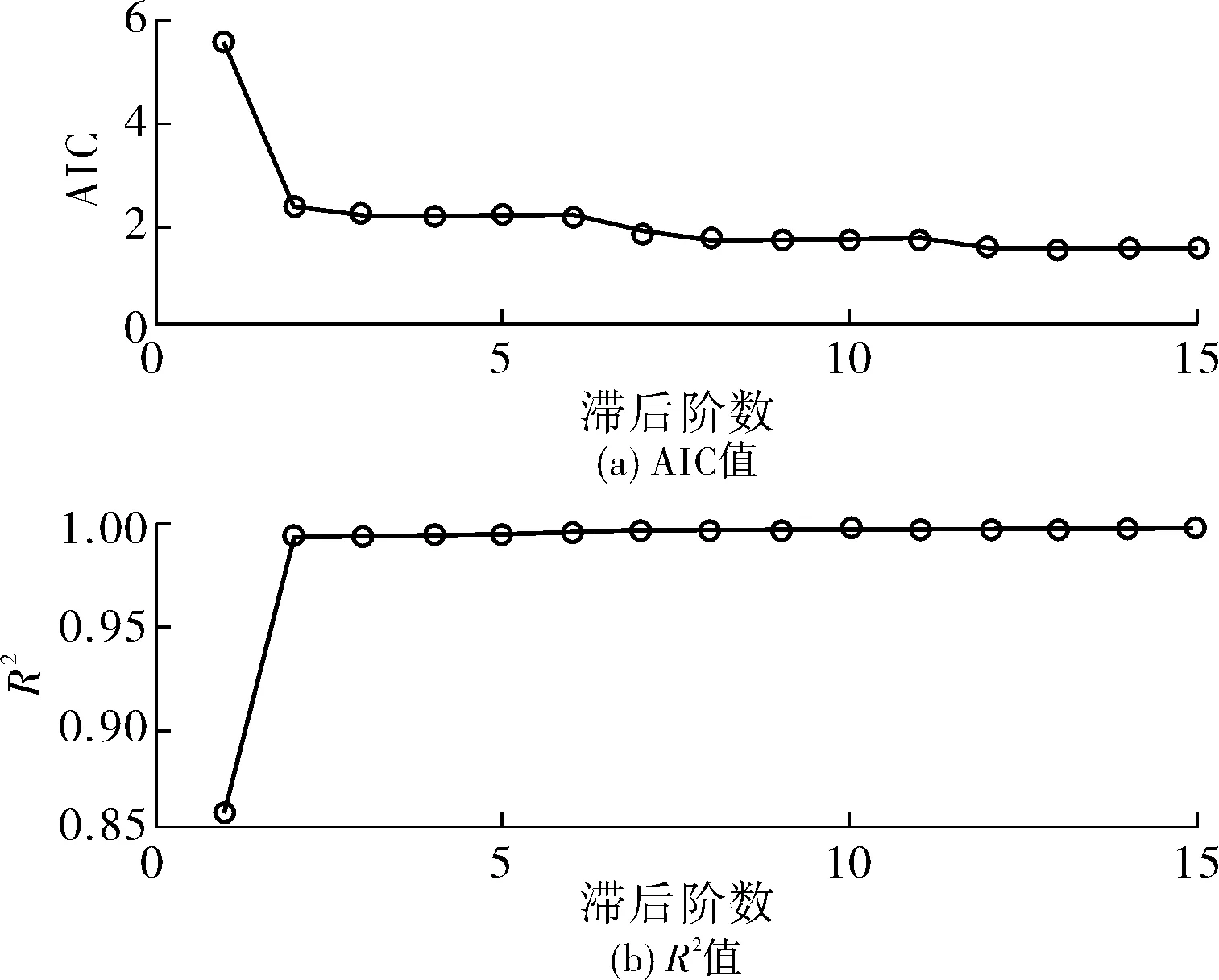
图9 AIC与R2变化
4)参数估计。确定模型阶数之后,利用最小二乘估计常数项和各系数的值。
5)异方差检验。对AR(4)模型的残差进行异方差检验,由表3可知,滞后阶数在1阶后P值等于0.551,即不拒绝H0,认为异方差效应不明显,故选择AR(4)模型。
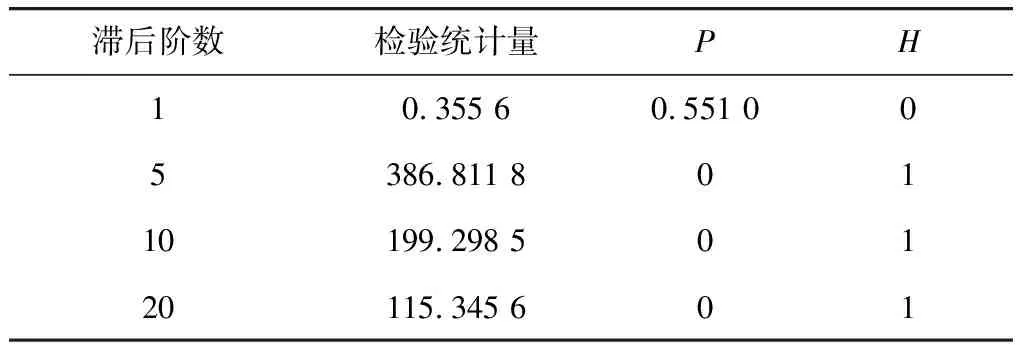
表3 异方差性检验
取每种损伤工况下所有测点DI值的均值作为该损伤工况所对应的DI值,结果如图10。
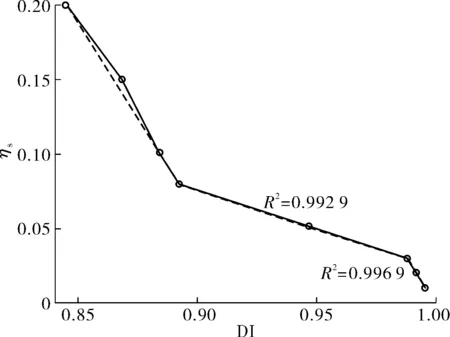
图10 DI与ηs关系
从图10可以看出,随着损伤程度的增加,各工况下的DI值逐渐减少,从而可以说明结构已经发生了损伤。将不同锈蚀率下的DI值进行回归,得到锈蚀率与DI值之间的对应关系为:
(16)
利用式(16),根据所计算的实际DI值即可推算出结构实际的锈蚀率,即实现了结构损伤程度的识别。从式(11)中可以知道,钢筋锈蚀深度不仅与钢筋锈蚀率有关,还与钢筋直径有关。
为此,笔者提出一种适用于不同钢筋直径的锈蚀率识别方法。仔细观察式(16)后可以发现,式(16)所描述的分段函数的两转折点所对应的锈蚀率与式(15)是一致的,且转折点之间呈线性关系,于是只要确定了各转折点的锈蚀率ηs与损伤特征指标DI关系,就可以写出整个分段函数的表达式。图11是B1/B0与DI之间的关系,由非线性拟合得到。
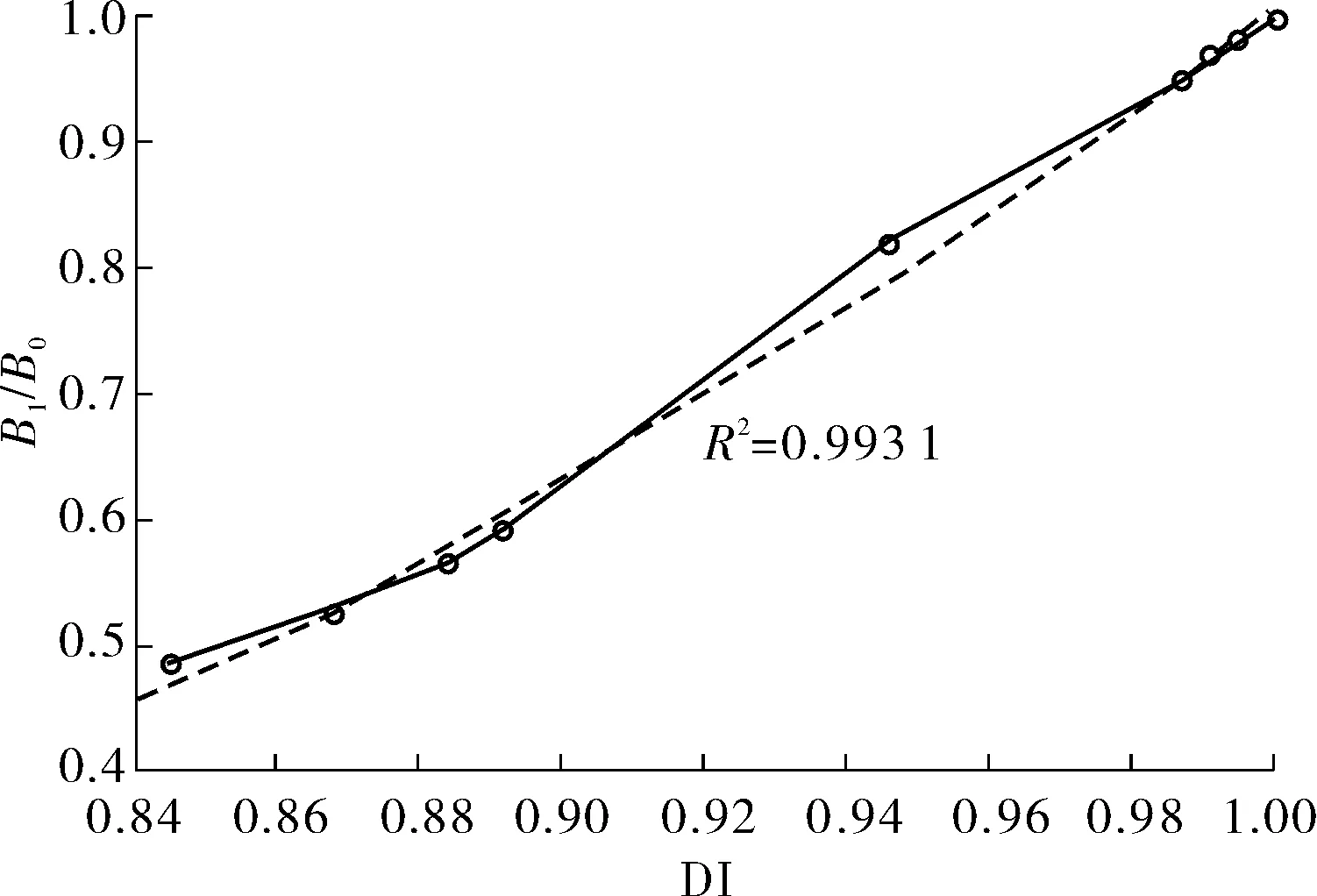
图11 DI与B1/B0关系
(17)
因此可按以下步骤识别不同直径钢筋的锈蚀率:
1)输入钢筋半径r,根据式(11)、式(15)计算两转折点所对应的锈蚀率ηs1、ηs2(设ηs2>ηs1)。
2)取ηs3>ηs2,按式(14)、(17)计算ηs1、ηs2、ηs3所对应的DI值。
3)根据点(1,0)以及上面求得的3个点,即可分段写出锈蚀率与DI之间的对应关系。
4)根据实测响应数据,按图2流程计算DI,并用第3)步求得的函数关系计算锈蚀率。
2.5 锈蚀RC拱损伤识别
本小节基于1#拱实测加速度响应数据,按2.4节所建立的DI与ηs之间的定量关系,实现了锈蚀RC拱损伤识别,并与实测锈蚀率对比,以此验证所提方法。
由于试验条件的限制,未能在1#拱未锈前进行加速度响应数据的采集,故以0#拱的加速度数据作为1#拱在未锈状态下的响应数据。
提取各测点(测点编号见图3)响应数据中包含峰值点、衰减段的5段样本数据,每个样本段有500个数据点。选取AR(10)模型建立时序模型,并提取DI,送入式(16)进行预测,计算结果见表4。
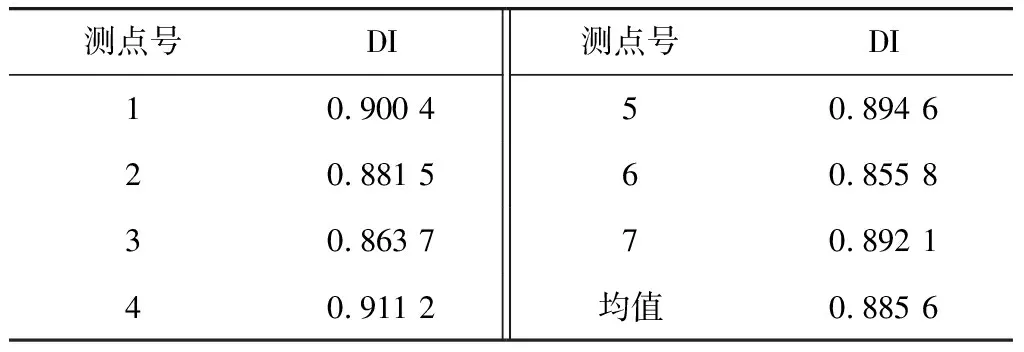
表4 试验计算结果
将表4的计算结果代入式(16),得到计算的锈蚀率为9.73%。与表1实测的锈蚀率对比可知,存在2.86%的误差,表明笔者提出的识别模型效果较好。分析造成此种误差的原因,主要有以下几点:拱圈并非均匀锈蚀,运用式(16)产生了相应的系统误差;不能完全保证完好状态和锈蚀状态下的激励一致,因为残差方差不仅会因结构损伤发生变化,还会由于激励大小、采样频率、模型阶数、环境因素等不同而发生变化。这些也是后续研究中需要着手解决的问题。
3 结 论
1)针对钢筋锈蚀导致的钢筋混凝土拱结构损伤,提出了基于加速度时间序列分析的损伤识别方法,建立了钢筋锈蚀与结构刚度退化的关系模型,并依此进行了数值仿真,在通过模型试验静力测试数据验证数值模型的合理性的基础上,得到了不同损伤工况下的结构动力响应,根据所提时序建模方法计算损伤特征指标,获取了锈蚀率与损伤特征指标之间的定量关系,提出了针对不同钢筋直径的锈蚀损伤识别模型。
2)利用模型试验所获得的加速度响应数据,对提出的基于时序分析的RC拱桥损伤识别方法进行了验证,计算结果与试验结果差异仅为2.89%,证明了该识别方法的有效性。
笔者所采用的基于残差方差的损伤特征指标对于激励大小、环境因素的敏感性仍有待进一步的分析,这也是作者未来努力的方向。
