海洋气象环境影响下的复杂水域船舶路径规划
2021-03-05谢新连魏照坤
谢新连,刘 超,魏照坤
(大连海事大学 交通运输工程学院 综合运输研究所,辽宁 大连 116026)
0 引 言
近些年来,随着我国经济快速发展,航运业运输量及船舶数量日益增大,海上施工项目的数量也不断增加,施工过程中形成的复杂水域可能会造成通航船舶碰撞,因此在复杂水域内如何确保船舶安全避开障碍物成为人们越来越关注的问题。同时,随着船舶智能化发展,基于电子海图的路径规划算法成为保证船舶安全航行的一种有效方法。目前,船舶路径规划算法一般有以下两种:一是将海图信息散化为网格,利用搜索算法生成最优路径[1-2],常用的搜索算法有启发式搜索算法、神经网络算法、遗传算法、蚁群算法等,部分学者采用两种算法结合的方法弥补单个算法存在的缺点;二是将海图中障碍物通过凸包算法理想化为凸多边形,利用可视图[3]、维诺图或MAKLINK图[4-5]生成初始可行路径,再通过搜索算法以最短距离为目标生成最优路径,也存在少量以能源消耗最少为目标的研究,并考虑了流对船舶航行的影响[6-7]。
综合上述研究可以发现,现阶段复杂水域船舶路径规划算法多存在以下不足之处:一是对海洋气象环境因素考虑不足,较少同时考虑风浪及流对船舶航行的影响;二是其搜索算法直接生成的路径平滑性较差,大多需要对路径进行再次调整。因此,为提高自动生成路径的质量,笔者将风浪流因素同时考虑在内,以船舶安全避开障碍物为前提,以航行时间最短为目标进行复杂水域船舶路径规划,提高了生成路径的安全性与经济性;并通过改进粒子群算法对初始路径进行优化,实现了在缩短路径航行时间的同时提高路径的平滑性。
1 海洋气象环境影响模型
1.1 海流对航速的影响模型


图1 海流对船舶航速影响示意
(1)
1.2 风浪对航速的影响模型
风浪对船舶航速的影响并未形成统一的研究方法,文献[8-9]利用数理统计的方法,通过分析船舶实际航行资料,拟合出了风浪影响下的船舶失速公式;文献[10-11]通过分析船舶航行时的附加阻力确定了船舶的失速。现阶段风浪对航速影响采用比较多的是R.L.TOWNSIN的拟合模型,该模型综合考虑了风浪的影响,按照式(2)计算:
(2)
式中:δv为航速改变量;α为船舶减速系数[12];μ为定向降速系数[13];N为蒲式风力表中的风级;Δ为船舶排水量。其中,α取值与船型、航速有关,见表1(Fr为船舶弗劳德数,Cb为船舶方型系数)。μ与风浪和船舶航向的夹角ε(后文统称为遭遇角,如图2)相关,其对应关系见表2。

表1 α取值
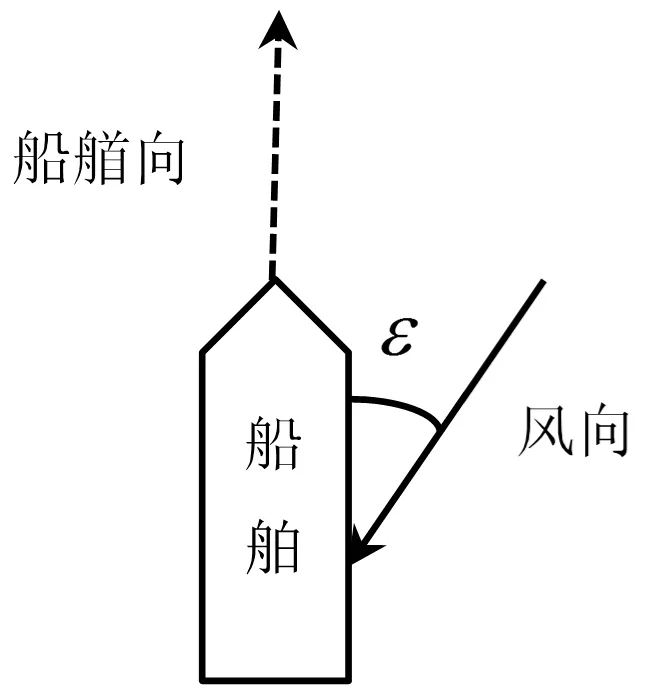
图2 遭遇角ε示意

表2 μ取值
1.3 风浪流影响下路径权值的确定
假设船舶主机功率保持不变,即船舶静水航速大小保持不变,优化目标为航行时间最短,则船舶通过相邻两点之间的权值为当规划海域内海洋气象环境条件确定时,船舶通过相邻两点的时间。
1.3.1 任意相邻两点之间的距离
通过两点之间的经纬度数据计算两点之间距离,具体计算公式如式(3):
(3)
式中:D为相邻两点的距离;R为地球半径;(L,B)、(L′,B′)分别为相邻两点的经纬度。
1.3.2 流影响下两点之间的实际航速
流影响下的船舶实际航速取决于流的来向及船舶艏向,为了确定船舶艏向,将经纬度转化为平面直角坐标,采用墨卡托投影方式进行转化[14],具体公式如式(4)~式(5):
x=a×B
(4)
(5)
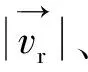
(6)
(7)
(8)
式中:(xH,yH)为船舶静水航速,由式(6)、式(7)联立计算得出。
1.3.3 风浪影响下两点之间的实际航速
假设风向为(xW,yW),根据式(2)计算风浪对航速的影响,其中遭遇角ε按式(9)计算:
(9)
1.3.4 任意相邻两点之间的航行时间
(10)
(11)
式中:v为风浪流影响下两点之间的船舶实际航速;t为船舶通过相邻两点之间的航行时间。
2 路径规划算法
2.1 生成初始可行路径
二维路径规划的可行空间可通过MAKLINK图构造而成[15]。由于风浪流对船舶航速的影响与船舶艏向有关,而船舶艏向取决于初始可行路径的方向,所以改进算法的有效性对于初始路径搜索方向的遍历性要求较高。但传统MAKLINK图在障碍物较多区域内产生可行点较多,终点附近产生可行点较少,不能充分保证终点附近搜索方向的多样性。基于此,提出改进MAKLINK图论生成初始可行点。具体生成方法如下:
步骤2:任意两个障碍物之间连线,将连线中与障碍物相交的连线删除,剩余连线的中点加入集合V;在终点到边界的垂线上均匀生成点,判断该点是否在障碍物内,若在则删除该点,如果该点不在障碍物内则保留该点,将剩余点加入集合V;将规划路径的起点和终点加入到集合V中,记集合V={vf|f=1,2,…,F},F为可行点数量。
步骤3:建立F行F列矩阵F,F元素取0或1,若为0,则该条路径可行,若为1,则该条路径不可行。将可行点集合V中的任意两个点进行连线,判断连线是否与障碍物相交,若相交,则删除该线,并将对应F矩阵中的数字记为0,否则,保留该线,将对应F矩阵中的数字记为1。剩余连线记为集合L={lj|j=1,2,…,J},J为可行连线的数量,L为初始可行路径集合。
2.2 初始路径规划
采用Dijkstra算法进行初始路径规划,其算法流程如图3,其中风向为X,起点为S,终点为T,永久节点集合为P,新加入永久点集合P的节点为k,临时节点集合为Q,永久点k的标号为Pk,临时点j的标号为Mj,从起点到节点j最短路径的前一个点为λj。
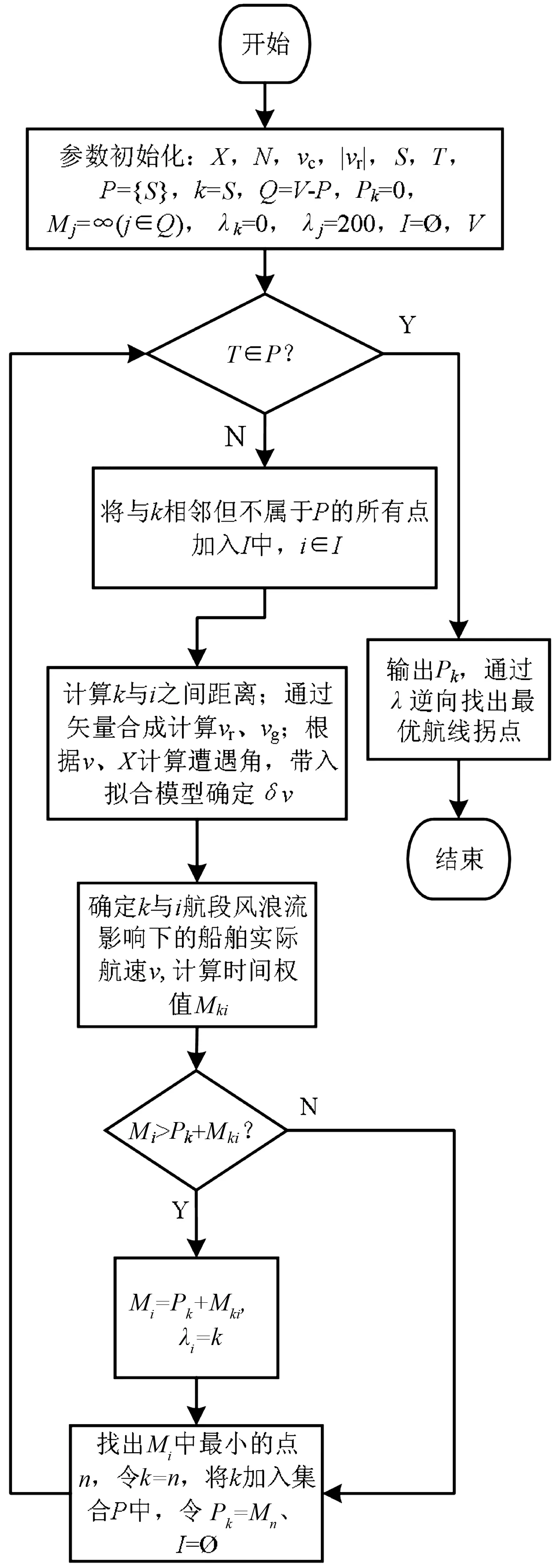
图3 算法流程
2.3 改进粒子群算法优化路径
由于Dijkstra算法搜索生成的路径基于虚拟生成的点,不可能遍布海域中所有点,其生成的路径可能存在偏差,且其平滑性较差。现阶段学者多先通过启发式算法减小搜索偏差,再通过路径调整改善路径平滑性[4-5];且其采用的启发式算法大多只能在MAKLINK中线上进行搜索,未能将中线附近的点考虑在内[4,14]。而文中的改进粒子群算法,不仅可以在缩短路径航行时间的同时增加路径的平滑性,而且可以搜索到MAKLINK中线附近的点,提高了求解的精确性。传统粒子群算法通过学习寻找全局最优解,改进PSO算法根据节点的相邻节点位置确定粒子飞行速度。
2.3.1 解的表示形式
第i个粒子搜索路径的顶点个数为Ni,其第t次迭代的搜索路径为xt,i={xt,i(1),xt,i(2),…,xt,i(Ni)},对于所有的i和t,其中xt,i(1)=S、xt,i(Ni)=T。
2.3.2 粒子飞行速度更新规则
传统PSO算法根据粒子群总体和个体最优值更新粒子速度,粒子飞行速度根据其相邻节点的位置确定,其具体方法为:
(12)
(13)
(14)
式(12)、式(13)表示点xt,i(p)在第t+1次迭代时的速度vt+1,i(p)取决于其前一个点xt,i(p-1)、后一个点xt,i(p+1)及初始速度vt,i(p)。其中:ω为惯性权重;r1和r2是(0,1)之间的随机数。式(14)表示点xt,i(p)在t+1次迭代中的位置xt+1,i(p),其具体关系如图4。

图4 粒子更新规则
提出的粒子速度更新规则使新的最优路径不断向障碍物靠近,且相邻两条线夹角逐渐增大,所以改进PSO算法可在缩短路径航行时间的同时增加路径的平滑性。路径的平滑性用除起点终点外,其余所有点的相邻两条线的夹角来衡量,如式(15):
(15)
2.3.3 路径可行性调整
由于粒子速度在更新时并未考虑到障碍物,其新生成的路径xt+1,i可能会与障碍物相交,所以应对其进行可行性检验。若相交,则应对路径进行调整,设与障碍物相交的点集为AP,则AP内的点在t+1时刻的位置如式(16):
(16)
改进粒子群算法如下:
t←1
while(满足最大迭代次数或停止条件)
for 每条路径i
计算其航行时间
end
对所有路径进行排序,更新最优路径
for 每条路径i
根据公式(12)至(14)更新vt+1,i和xt+1,i
while 存在不可行路径
定义相关的不可行点集AP
根据式(16)调节xt+1,i(AP)
end
end
t←t+1
end
3 仿真算例
3.1 算例求解
以一艘4 500 TEU集装箱船为例,船舶参数见表3,验证海洋气象环境影响下船舶路径规划算法的有效性。经过多次试验,证明算法有效,选取规划海域环境模型如图5,图中多边形为将海图中障碍物凸多边形化处理后得到的模型,S、T分别为起点和终点。

表3 船舶参数
当风向与起点到终点方向(统称为初始航向)夹角为0°、风力为7级,海流方向为东偏北60°、大小为1.5 kn,图5中实线为考虑海洋气象环境影响的船舶路径规划算法(统称为改进算法)求出的初始规划路径,航行时间为10.03 h;点划线为改进PSO算法优化后的路径,航行时间为9.70 h;图中虚线为不考虑海洋气象环境影响的船舶路径规划算法(统称为传统算法)求出的优化路径,航行时间为10.67 h。二者生成的路径均可以安全避开障碍物,虽然前者比后者生成的优化路径多一个转向点,航行距离更远,但航行时间节省了9.15%。
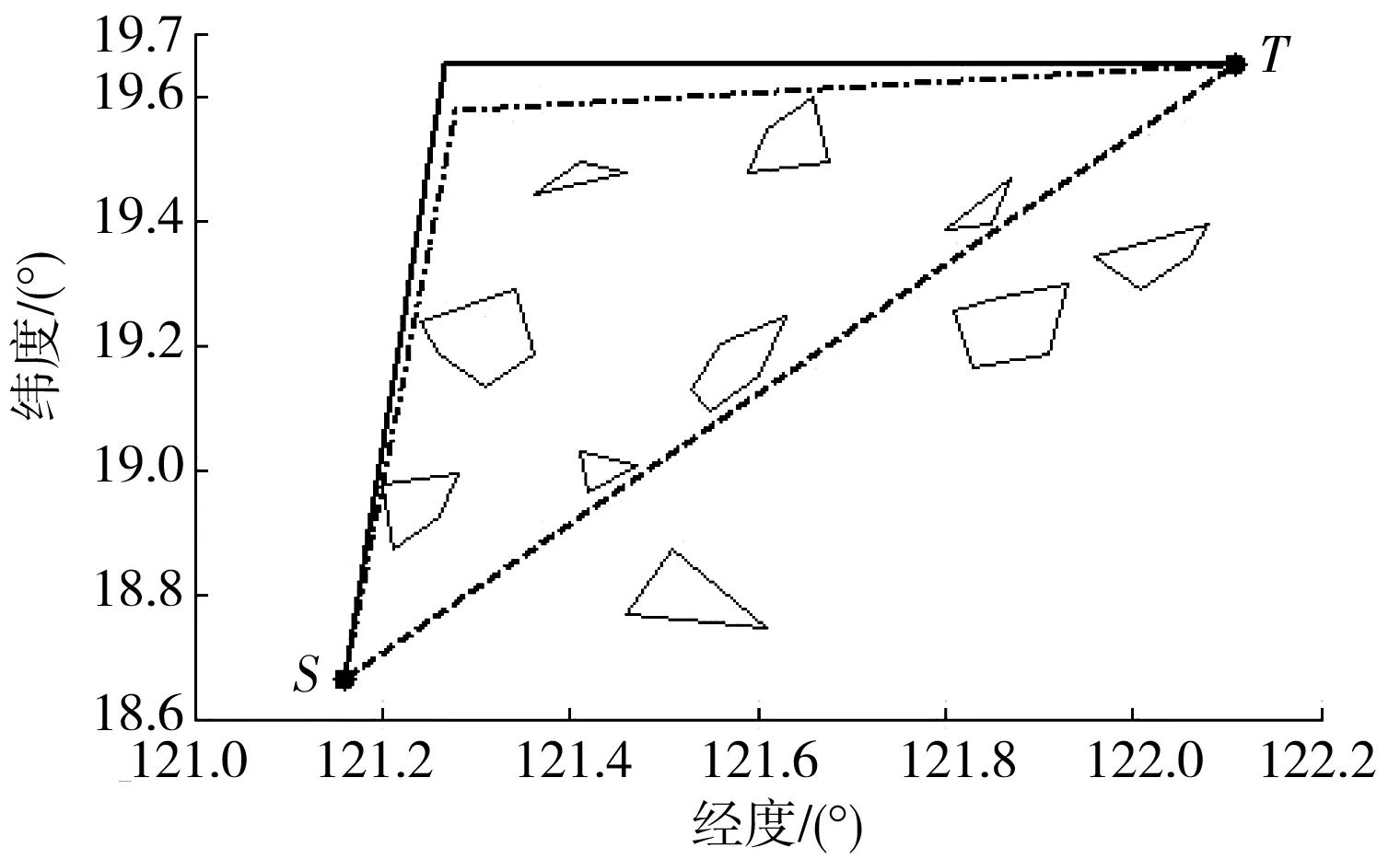
图5 两种算法生成路径的对比
表4为改变船舶起点、终点时,改进PSO算法优化前后路径航行时间与平滑性的对比,表中IL为初始路径航行时间,FL为改进PSO算法优化后的路径航行时间,IC为初始路径平滑性,FC为改进PSO算法优化后的路径平滑性。从表中可以看出,改进PSO算法在缩短路径航行时间的同时也可增加路径的平滑性。

表4 改进PSO算法有效性分析
3.2 敏感性分析
由于海流对船舶航速影响较小,所以只对风浪进行敏感性分析。通过拟合模型分析风浪对船舶航 速的影响,风力为8级时,船舶航速大幅下降,此时,船舶航行优先考虑安全性,所以研究风级范围为8级以下。
3.2.1 风向敏感性分析
选取风向与初始航向的夹角为变量、逆时针方向为正方向,步长为1°,具体结果如图6,图中纵坐标为改进算法生成的路径比传统算法生成的路径节省的航行时间。图7为不同风向下改进算法生成的路径。
从图6可得,风向变化对改进算法生成路径节省的航行时间影响较大;当风向与初始航向夹角为90° 或180°时,不论风级如何变化,改进算法生成路径节省的航行时间较少;当风向与初始航向夹角为0°~60°或130°~150°时,改进算法生成路径节省的航行时间较多。

图6 不同风向下改进算法节省的时间
从图7可得,当风级较小时,如4级、5级风,改进算法生成的最优路径在传统算法的最优路径附近波动,随着风级的增大,通过增加航行距离减小风浪对船舶航速影响的航行方法更合理,如6级、7级风,改进算法与传统算法生成的路径区别较大。

图7 不同风向下改进算法生成的路径
3.3.2 风级敏感性分析
风级变化对改进算法有效性的影响如图8,图中η为风向与初始航向的夹角,取值分别为30°,60°,150°,图例中E为改进算法生成路径的航行时间,D为传统算法生成路径的航行时间,P为改进算法比传统算法生成路径节省的航行时间百分比。

图8 不同风级下两种算法的对比
从图8可得,在风向与初始航向夹角的有效范围内,不论其夹角为多少,随着风级的增大,改进算法比传统算法生成路径节省的航行时间逐渐增大。
4 结 论
为了使复杂水域内船舶自动生成的路径更加符合实际,以航行时间最短为目标,设计了考虑海洋气象环境影响的船舶路径规划算法。以一艘集装箱船通过规划海域为例进行算例检验,得到以下结论:
1)在路径规划中,考虑海洋气象环境对船舶航速的影响,生成的路径更加符合实际,且其安全性和经济性更好。
2)设计的路径自动生成算法不仅可以保证船舶安全避开障碍物,而且比传统算法求得的优化路径更加节约航行时间,算法具有有效性。
3)提出的改进粒子群算法在缩短初始规划路径航行时间的同时还可增加路径的平滑性。
4)风级一定,随着风向变化,改进算法生成的路径节省的航行时间变化较大,当风向与初始航向夹角为0°~60°或130°~150°时,节省的时间较多;风向一定,随着风级的增大,算法生成的路径节省的时间逐渐增大。
综上所述,设计的船舶路径规划算法能够为船舶通过复杂水域生成一种合理、有效的路径。
