基于集合经验模态分解的脑电信号高阶张量特征提取

付荣荣， 杨 阳， 于 宝， 刘 冲， 张 驰

(1.燕山大学 电气工程学院，河北 秦皇岛 066004；2.东北大学 机械工程与自动化学院，辽宁 沈阳 110819；3.大连理工大学 生物医学工程学院，辽宁 大连 116024)

1 引 言

脑电信号(electroencephalography，EEG)是由大脑神经元活动产生的信号，其中包含了丰富的大脑状态信息，为实现脑-机接(brain-computer interface，BCI)需要对脑电信号进行有效解码，解码过程包括对EEG信号进行特征提取和模式分类。传统的BCI多通道EEG信号特征提取方法有AR模型、时频滤波方法、共空间模式、主成分分析和2D主成分分析(2DPCA)等[1～3]，这些从时频域或时空域提取特征方法都已取得不错的效果。但是，这些二阶特征提取方法必然会忽略频域或空间域的特征，限制了所提取特征被准确识别的上限。近年来，Lu H等[4]提出了多线性主成分分析(multi-linear principal component analysis，MPCA)等高阶特征提取方法，这种高阶特征提取方法不需要将原始数据展开成向量形式，保留了数据的结构特性。随后，一些研究小组开始研究时空频高阶特征提取方法，文献[5,6]提出了一种基于小波和独立分量分析的时间频率空间EEG特征的提取方法，分别用离散小波变换和独立分量分析提取时频域特征和空域特征，有效地克服了传统的时频特征提取方法空间信息描述不足等问题；王金甲等[7]首先利用复Morlet小波分析方法生成张量数据，然后进行张量降维并提取特征，克服了主成分分析维度小的局限性。可见高阶特征提取方法在单次运动想象脑电信号的特征提取中是极为有效的，但小波分解方法构建高阶张量时存在小波参数难以确定的缺陷。

针对上述问题，本文提出了一种新的特征提取方法，这种方法通过集合经验模态分解[8～11](Ensemble Empirical Mode Decomposition，EEMD)提取EEG频域信息，构造包含频域、时域、空间域的三维EEG信号；并结合MPCA对EEG信号进行降维。这种新的高阶特征提取方法无需将原始脑电信号张量展开为向量，能够分别从时域、频域和空间域提取脑电信号的多模态特征。通过与使用小波分解构建EEG高阶张量并使用EEMD进行降维的特征提取方法和直接使用2DPCA[12]方法进行降维的特征提取方法进行对比，验证了本文提出方法的有效性，为单次运动想象脑电信号的准确识别奠定了基础。

2 实验方法

2.1 脑电信号的采集

实验共7名受试者参与脑电信号的采集，年龄在22～27岁之间，实验前已被告知实验过程并签署知情同意文件。实验采用虚拟碗球实验，这是一种动态复杂约束特性的脑电实验，实验环境包括演示刺激系统和脑电信号采集系统两部分。演示刺激系统为一台在PsychToolbox环境下运行虚拟碗球系统的计算机，脑电采集系统为Emotiv的EPOC+。

在正式实验之前，参加实验的7名受试者需要先进行虚拟碗球实验的模拟练习。在整个实验中，受试者正坐在椅子上，目视前方的演示刺激系统电脑屏幕。

演示刺激系统电脑屏幕上显示内容为虚拟碗球系统，受试者需要控制碗在水平面上从起点到达终点，碗里的球此时会由于惯性在碗中晃动，受试者同时还必须将球约束在碗中，如果球从碗中掉出，实验会被立即终止。按压电脑键盘的左右键就能控制碗左右移动，在按压左右键的同时，受试者还需要想象对应的左右运动。在实验过程中，通过Emotiv的EPOC+对脑电信号进行采集。信号采集示意图如图1所示。

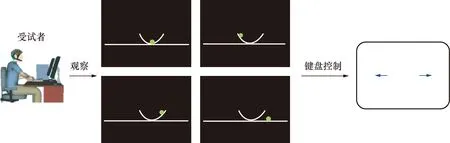
图1 EEG信号采集示意图Fig.1 EEG signal acquisition diagram

2.2 脑电信号的预处理

通过脑电采集设备采集到的脑电信号非常微弱而且含有噪声，需要对信号进行预处理[13]。由于运动想象诱发的ERD/ERS[14]现象主要集中在Mu节律和Beta节律，即要分析的信号频率范围为8～30 Hz，故采用8～30 Hz的6阶巴特沃斯带通滤波器对采集到的原始数据进行滤波。经过Emotiv的EPOC+能够采集到14导联的脑电数据，采样频率为128 Hz。经过预处理后将14通道的脑电数据[15]划分为2个类别，将数据逐次截取每一类别的前1 s数据，整理为多个四维张量结构(样本点数目×导联数目×实验次数×类别)。

2.3 对照实验

为了验证新提出的特征提取方法的有效性，设计了3种不同特征提取方法的对照实验。实验1为本文提出的特征提取方法，采用EEMD构建脑电信号高阶张量，采用EEMD进行降维，流程图如图2所示；实验2采用复Morlet小波分解构建脑电信号高阶张量，采用MPCA进行降维；实验3直接对采集到的EEG信号进行2DPCA进行降维。特征提取后都采用Fisher线性判别分析分类方法取得分类准确率。由于EEG数据集采集难度大，数据集较小，为获得更佳的模型，本实验采用10折交叉验证将数据随机分为90%的训练集和10%的测试集进行分类。

图2 本文提出的特征提取方法流程图Fig.2 The flow chart of feature extraction method proposed

3 算法原理

3.1 EEMD方法

对单次运动想象的脑电信号，其数据形式为样本点×导联数目，分别表示脑电信号的时域信息和空间域信息。为了获得更加全面的脑电信息，需要对采集到的时域信息进行时频变换。本方法采用EEMD进行时频变换，EEMD方法依据数据自身的时间尺度特征进行信号分解，无需设定预先设定的任何基函数，对于处理非线性非平稳时间序列非常有效。经过EEMD处理后，脑电数据同时包含了脑电的时域信息，频域信息和空间域信息。

EEMD的原理是先将频谱均匀分布的白噪声加入原信号中作为新的待分解信号，这样不同时间尺度的信号就自动分布到了合适的参考尺度。再将信号进行经验模态分解(empirical mode decompose-tion，EMD)[16～18]处理，由于白噪声零均值的特性，最后取均值得到逼近真实的模态。具体步骤如下：

(1) 往信号x(t)中输入白噪声信号k·σx·n(t)，其中：n(t)为归一化白噪声，σx为信号标准差，k为比例系数，得到信噪混合函数，

y(t)=x(t)+k·σx·n(t)

(1)

(2) 确定信号y(t)的所有局部极值点。

(3) 利用3次样条插值将所有局部极值点连接起来分别形成上、下包络线包络所有的数据点。

(4) 上、下包络线的平均值记为m1(t)，

h1(t)=y(t)-m1(t)

(2)

(5) 如果h1(t)满足在整个数据段内，极值点的个数和过零点的个数必须相等或相差最多不超过一个且上、下包络线相对于时间轴对称，则h1(t)就是y(t)的第一个本征模态函数(IMF)分量，否则y(t)=h1(t)，重复(2)至(4)。

(6) 将h1(t)从y(t)中分离出来得到，

r1(t)=y(t)-h1(t)

(3)

重复(2)～(5)。

(7) 最终将y(t)分解成IMF的组合，

(4)

式中rm(t)为分解m次后的剩余分量。

3.2 MPCA方法

得到了包含脑电的时域信息，频域信息和空间域信息的脑电信号后，需要对脑电信号进行降维，从而剔除对脑电信号分类影响很小甚至误导分类的部分特征(噪声)。

本方法对脑电数据使用MPCA进行降维。MPCA算法的目的是找到多个模态的投影矩阵1U(1)T，21U(2)T，31U(3)T，…，n1U(n)T来对原始张量数据进行降维，并尽量保持原张量组的离散度。由于本研究脑电信号提取了频域、时域、空间域三维信息，以三阶张量为例，具体步骤如下：

(1) 对所述张量样本X∈1Uc×f×t×s进行中心化处理，其中，c为空间域信号，f为频域信号，t为时域信号，s为实验次数。

(5)

其中，

(6)

(2) 计算初始协方差矩阵，

(7)

式中：Xm(n)为Xmn模展开后的矩阵，并对所述初始协方差矩阵进行特征分解，取最大的d′个特征值对应的特征向量组成投影矩阵1U(n)(n=1，2，3)得到初始化的降维投影矩阵。

泼水节是傣族人民的传统节日，傣族人民喜水，不仅与气候环境文化传统有关，更是一种风俗习惯，傣族是一个热爱水的民族。在傣族社会中,水不仅仅是一种自然的物质,同时也被赋予了丰富的文化内涵,从而形成了自身的水文化。水文化作为一种重要的社会传统,在保持傣族居住区人与自然环境的和谐起到了积极的作用。历史上傣族和水就有一种特殊的关系,并且傣族拥有生动的水文化,因此大多数傣族被其他民族生动地称为“水傣”。根据傣族人类起源的传说,天空和大地都起源于水,而且认为人类生命的一半也是由水创造。因此水是无比伟大和圣洁的。

(3) 对步骤(2)得到的所述初始化降维投影矩阵进行局部优化，包括如下具体步骤：

① 进行投影，

(8)

式中左下标1、2、3表示1模、2模、3模乘积。

② 计算总散度，

(9)

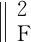
③ 对n=1、2、3，计算投影后张量n模展开后协方差矩阵的特征值，取d′个所述特征值对应的特征向量组成新的投影矩阵1U(n)(n=1，2，3)，用所述新的投影矩阵更新Sm并计算新的ψSk；

④ 判断ψSk-ψSk-1<η是否成立，式中k为优化迭代次数，η为自定义的阈值，如果ψSk-ψSk-1<η，得到最终的投影矩阵11U(1)T，21U(2)T，31U(3)T，计算

(10)

得到的投影矩阵21U(2)T，21U(2)T，31U(3)T即为MPCA要求的投影矩阵。对原始数据进行投影就得到了降维后的脑电数据。

3.3 Fisher线性判别分析

降维后的脑电数据是三阶多维脑电信号，需要先将其展开为一阶多维信号，然后使用分类器进行分类。本实验采用Fisher线性判别分析[13]方法对数据进行分类。线性判别分析的思想为：使投影后类内间距最小，类间方差间距最大。具体步骤如下：

(1) 计算出两类数据特征向量的均值向量

(11)

式中Nj为第j类特征向量对应的数据点数。

(2) 将二者方差加起来求出类内散度矩阵

(12)

(3) 计算类间散度矩阵Sb

Sb=(m0-m1)(m0-m1)T

(13)

(5) 计算投影后的数据点Y。

Y=WTX

(14)

4 实验结果

4.1 分类结果评价

表1为实验分类结果，ACC(Accuracy)为准确度，AUC(Area Under Curve)为受试者工作特性ROC(receiver operating characteristic)曲线下的面积，ACC值和AUC值越接近1代表分类结果越好。

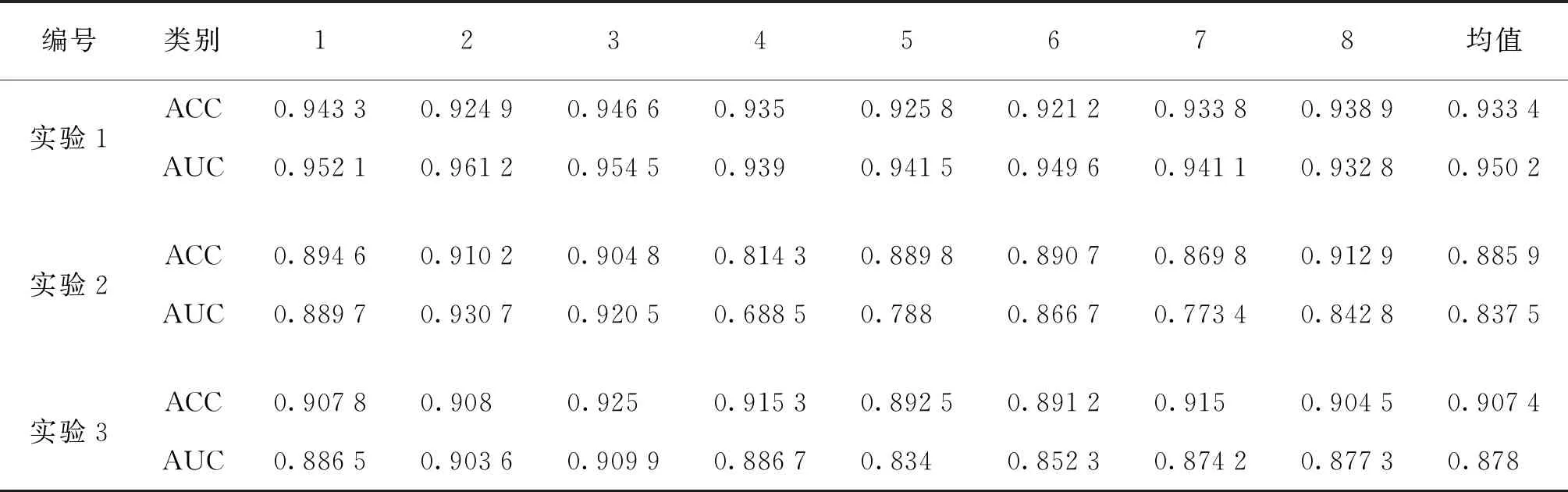
表1 实验分类结果Tab.1 Classification results of experiment

对比3种实验的AUC和ACC结果如图3所示。

由表1可以看出，实验1(本文提出的EEMD+MPCA方法)中8个受试者EEG信号的识别ACC均值为0.933 4，AUC均值为0.950 2都高于实验2(小波+MPCA)和实验3(2DPCA)的结果，由图3能够直观地看出实验1获得的AUC和ACC在每个实验对象上都是最高的，即实验1的方法比实验2和实验3能取得更好的分类效果。这个结果说明，采用EEMD构建脑电信号高阶张量，采用MPCA进行降维的特征提取方法相对于采用复Morlet小波分解构建脑电信号高阶张量，采用MPCA进行降维和直接对采集到的EEG信号进行2DPCA进行降维的特征提取方法而言能够取得更好的特征，在单次运动想象脑电信号识别中能够取得更准确的识别结果。

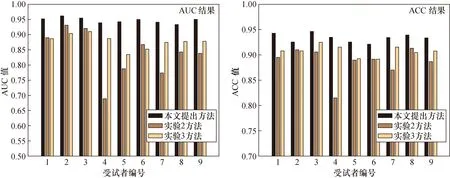
图3 3种实验的AUC和ACC结果对比图Fig.3 Comparison of AUC and ACC results of three experiments

4.2 适用性评价

由于脑电信号的个体差异，同一方法对不同受试者脑电信号的分类可能取得不同的效果，因此，分别计算了3种实验AUC和ACC的方差如表2所示。

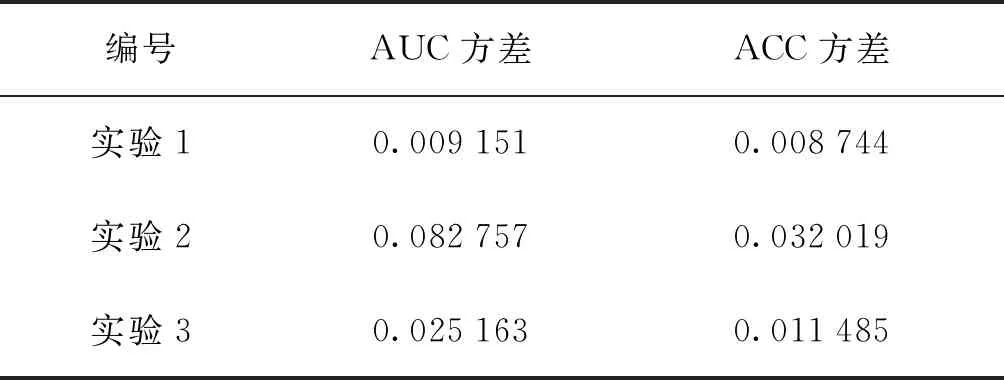
表2 3种实验AUC和ACC的方差Tab.2 Variance of AUC and ACC in three experiments

由表2可以看出：实验1的AUC方差为 0.009 151，ACC为0.008 744都远远小于实验2和实验3的方差；由图3也可以看出实验1每个受试者的AUC和ACC结果差别很小，而实验2和实验3每个受试者的AUC和ACC结果参差不齐，说明实验1的方法对于不同的受试者有更好的适用性。该结果说明：采用EEMD构建脑电信号高阶张量和采用MPCA进行降维的特征提取方法相对于采用复Morlet小波分解构建脑电信号高阶张量和采用MPCA进行降维，直接对采集到的EEG信号进行2DPCA进行降维的特征提取方法具有更高的适用性，在对不同个体的单次运动想象脑电信号识别中能够取得稳定的识别效果。

5 讨 论

本文提出的采用EEMD构建脑电信号高阶张量，MPCA进行降维的特征提取方法可以提取出对EEG信号识别最有效的特征。通过100次10折交叉验证取平均值得到的结果避免随机性，保证了分类结果的准确性。最终得到本特征提取方法结合Fisher线性判别分析能达到93.34%的准确率，比采用Morlet小波分解构建脑电信号高阶张量，MPCA进行降维，结合Fisher线性判别分析分类的方法准确率高4.75%；比直接对采集到的EEG信号进行2DPCA进行降维，结合Fisher线性判别分析分类的方法准确率高2.6%。并且，对8名受试者的分类准确率的方差也最小仅为0.008 744，比采用Morlet小波分解构建脑电信号高阶张量，MPCA进行降维，结合Fisher线性判别分析分类的方法准确率方差减小72.69%，比直接对采集到的EEG信号进行2DPCA进行降维，结合Fisher线性判别分析分类的方法准确率方差减小23.86%。这说明该方法对不同受试者的单次运动想象脑电信号都能取得很好的识别效果。

构建EEG信号高阶张量时，Morlet小波分解方法需要调节不同的小波参数来适应不同人的EEG信号才能取得更准确的分类结果，因此在不同人身上的识别准确率出现很大的差异性，甚至同一个人的不同次实验的识别准确率也会有较大的差异。

EMD分解方法由于具有自适应性，能够根据数据本身来分解数据，但是会出现模态混叠，同一个人不同次实验的分解长度不能对齐，不能用来构建EEG信号高阶张量。而EEMD分解方法在EMD分解信号中加入白噪声，继承了EMD优点的同时，解决了模态混叠现象，能够将EEG根据频率自适应分解。因此，在构建EEG信号高阶张量时，EEMD方法要优于Morlet小波分解方法。在整个EEG信号的分类识别中，基于EEMD方法构建脑电信号高阶张量，结合MPCA进行降维的特征提取方法提取了EEG信号时域，频域和空间域的多模态特征[19～20]，而直接采用2DPCA的方法忽略了EEG信号的频域信息，未能取得更好的识别效果。

本文将EEMD方法引入EEG信号高阶张量的构建，结合MPCA进行特征提取，使得在特征提取的过程中，不需要将原始高阶张量展开为向量，保留了脑电信号的时域，频域和空间域信息。并结合Fisher线性判别分析构成的算法组合用于单次运动想象脑电信号识别。采集脑电数据数据，设计对照实验，并通过100次10折交叉验证的方式避免了实验结果的随机性，验证了新提出方法的有效性。

6 结 论

本研究提出基于EEMD方法构建脑电信号高阶张量，结合MPCA进行降维的特征提取方法。通过与基于Morlet小波构建脑电信号高阶张量结合MPCA降维的特征提取方法和直接对脑电信号进行2DPCA降维的特征提取方法进行对比，结果表明：

(1) 本研究提出的特征提取方法能够提取更明显的特征，结合Fisher线性判别分析能够取得更高的分类准确率；

(2) 本研究提出的特征提取方法相对于上述其他两种特征提取方法对不同的受试者具有更好的适用性，能够更好的应用于不同个体。