基于反向共轴的大口径平面光学元件面形测量

赵彦龙， 李加福， 朱小平， 杜 华， 陈爱军， 胡佳成

(1.中国计量大学，浙江 杭州 310018；2.中国计量科学研究院，北京 100029)

1 引 言

由于大口径光学元件的面形质量直接影响光学系统的性能，故像惯性约束聚变激光驱动装置等庞大、复杂且系统性极强的超大型光学系统，对大口径光学元件的面形质量有极为苛刻的要求[1～4]。

针对大口径平面光学元件的面形测量，美国Zygo公司推出了基于移相干涉技术的大口径平面干涉仪，借助标准光学平晶，将准直光束分成参考光和待测光，两束光相干叠加形成干涉图像，实现面形相对测量，经过技术更新迭代，目前Zygo平面干涉仪最大测量口径φ914 mm，标准平晶参考面峰谷值比(peak to valley，PV)值可达63 nm[5～7]；2012年Gerd Ehret等基于五棱镜小角度扫描测量技术研制了水平式和垂直式两种大口径平面光学元件面形测量装置，最大测量口径接近φ1 000 mm，测量不确定度达亚纳米级别[8～10]；2013年文献[11]报道了所研制的近红外大口径波长移相干涉仪，最大测量口径φ600 mm，测量不确定度优于60 nm。

但对于大口径平面光学元件面形测量仍存在测量口径、测量精度和量值溯源等问题。

为了提升我国大口径平面光学元件面形测量能力，本文提出了一种基于反向共轴的大口径平面光学元件面形测量方法，将双位移传感器反向共轴线扫描测量模式和多角度旋转三面互检技术结合[12～17]，有效地扩大了测量口径并实现了面形绝对测量，测量结果直接溯源到激光波长基准，通过对φ400 mm口径光学平晶面形测量实验，验证了基于反向共轴的大口径平面光学元件面形测量方法的可行性。

2 基于反向共轴的大口径平面光学元件面形测量

2.1 测量方法

测量方法是以双位移传感器反向共轴线扫描测量模式与多角度旋转三面互检技术相结合。位移传感器反向共轴线扫描测量模式如图1所示，将一对高精度位移传感器以反向共轴方式安装于直线长导轨测量座上，对平面光学元件面形进行线扫描测量，这种测量模式借助直线长导轨有效扩大了平面光学元件测量口径，更换不同类型的传感器能够测量非光滑、不同材质的表面形貌。

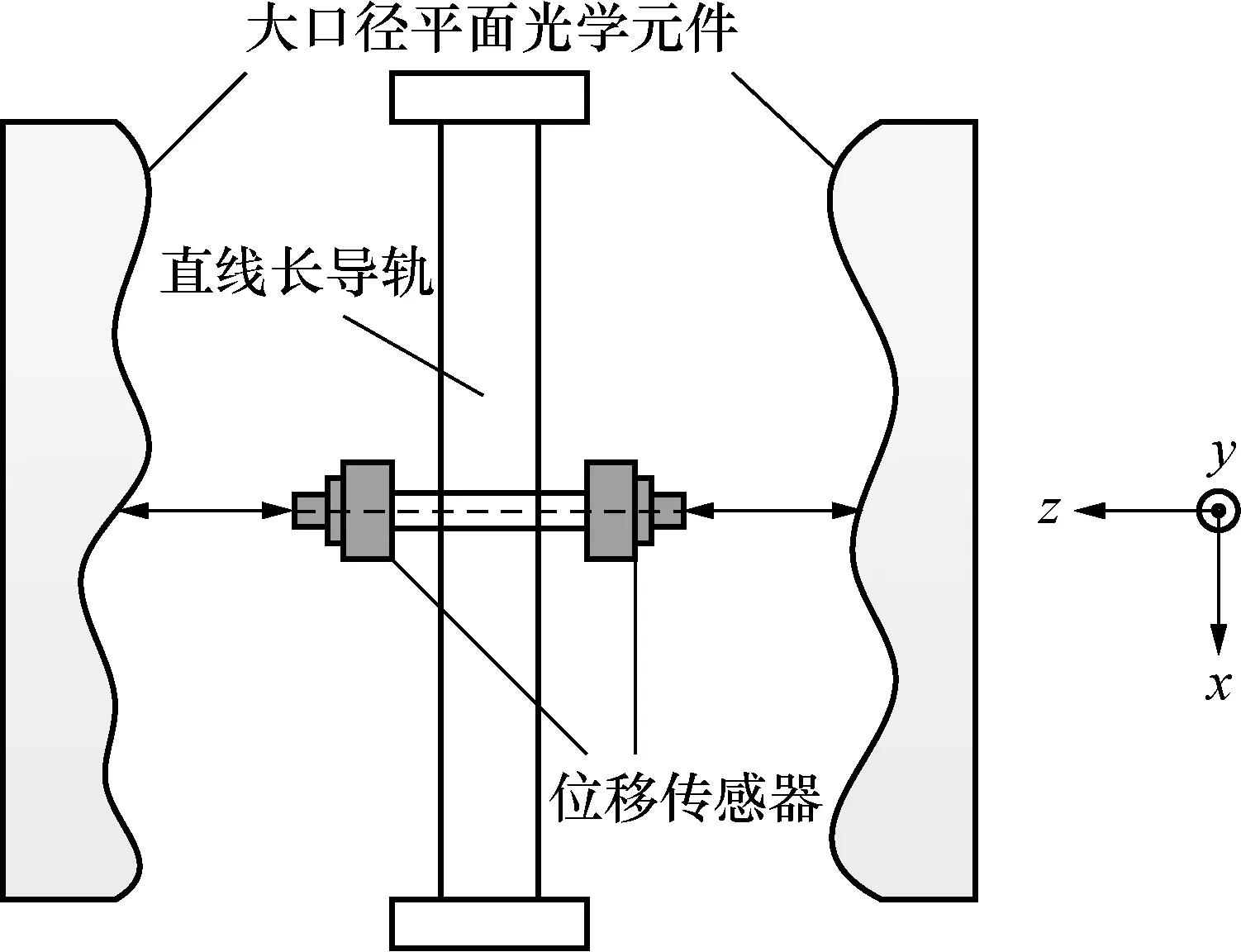
图1 反向共轴测量模式图Fig.1 Reverse coaxial measurement mode diagram

多角度旋转三面互检技术是对传统三面互检的改进。

传统三面互检三次组合测量仅能得到翻转对称中心线上的面形分布，而多角度旋转三面互检先将平面光学元件测量面两两组合，然后按角度θ多次旋转平面光学元件测量面，并依靠双位移传感器反向共轴测量模式按角度依次线扫描测量左右平面光学元件测量面面形，如图2所示，最后经三维面形重构和三面互检面形分离算法得到平面光学元件测量面多个方向上的面形分布。多角度旋转三面互检是一种面形绝对测量技术，测量过程中不需要使用标准平晶，避免引入标准平晶参考面不确定度分量产生的测量误差，测量结果直接溯源到激光波长基准。

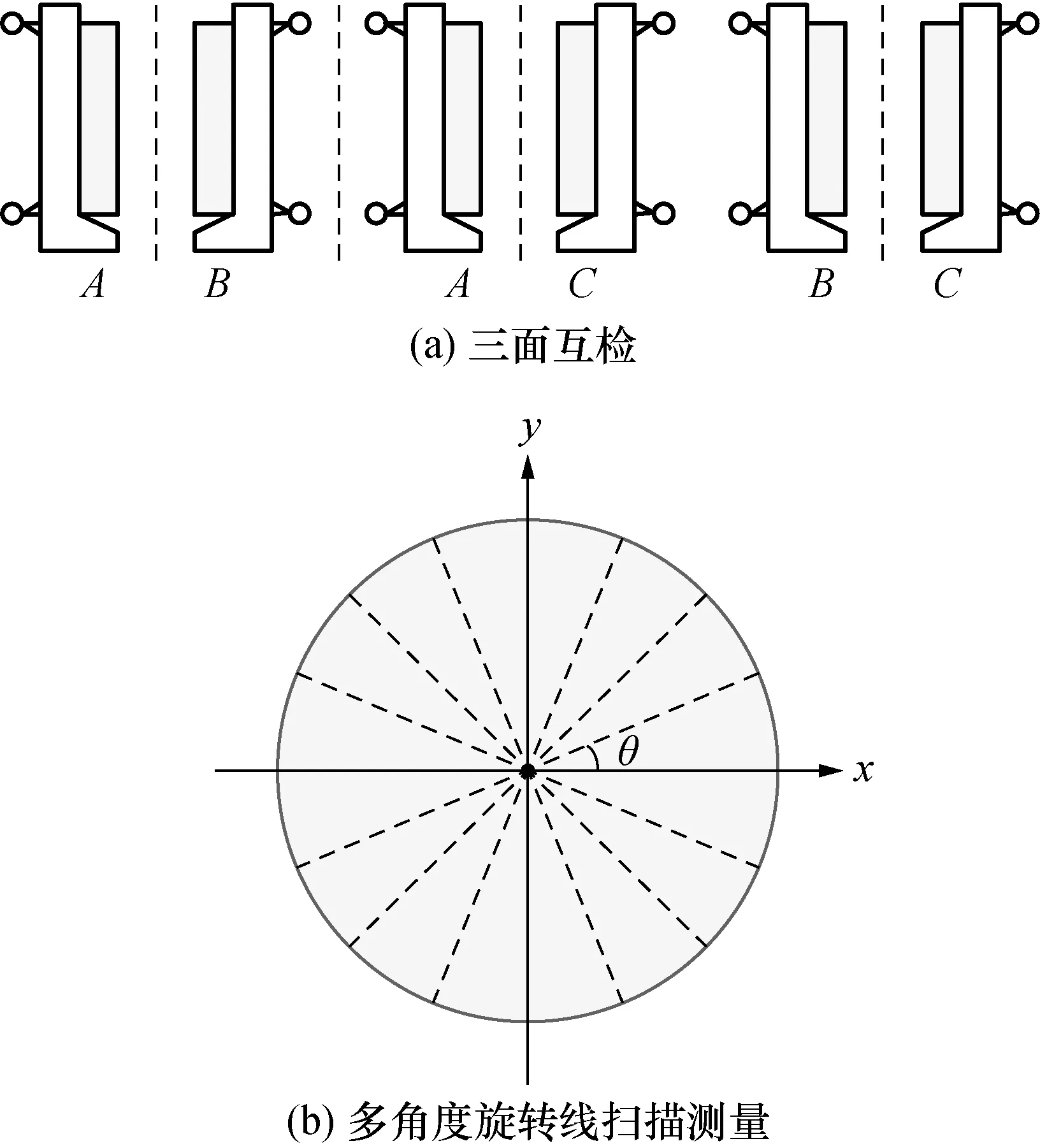
图2 多角度旋转三面互检图Fig.2 Three-flat test of multi-angle rotation diagram

基于反向共轴的大口径平面光学元件面形测量方法融合了双位移传感器反向共轴线扫描测量模式和多角度旋转三面互检技术的优势，能够实现大口径平面光学元件面形的绝对测量。

2.2 测量步骤

基于反向共轴的大口径平面光学元件面形测量方法测量流程如图3所示。

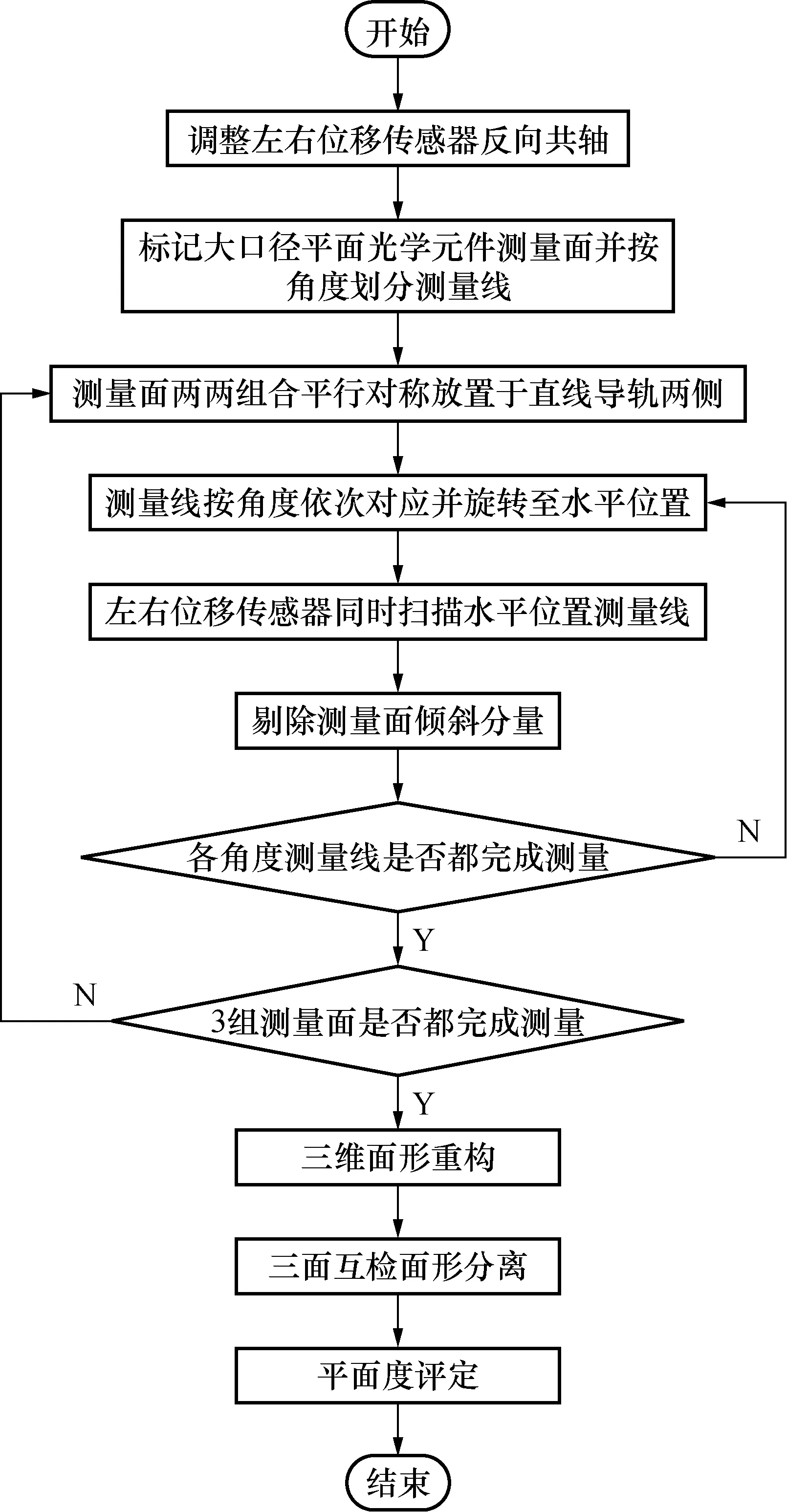
图3 测量流程图Fig.3 Measurement flow diagram

测量方法步骤如下：

(1) 选用一对同种型号的高精度位移传感器安装于大行程直线导轨测量座上，通过位姿调整机构调整左右位移传感器反向共轴。

(2) 将3块大口径平面光学元件测量面用A、B、C标记加以区分，并对每个测量面按角度θ划分测量线。

(3) 将大口径平面光学元件测量面A、B、C两两组合成AB、AC、BC，依次平行对称放置于大行程直线导轨两侧。

(4) 通过旋转机构旋转大口径平面光学元件测量面，先将左右测量面上的测量线按角度依次对应起来，再将其旋转至水平位置。

(5) 反向共轴的左右位移传感器沿直线导轨同时扫描左右大口径平面光学元件测量面水平位置测量线，并计算左右位移传感器线扫描测量面形之和，公式如下：

(1)

式中：θ∈[0°,180°)，lA,θ、lB,θ、lC,θ分别表示大口径平面光学元件测量面A、B、C中角度为θ的测量线面形分布，即lA,θ∈A，lB,θ∈B，lC,θ∈C；lg表示线扫描测量过程中直线长导轨在位移传感器测量方向的变化量；lAB,1,θ表示组合测量面为AB，测量线角度为θ的单侧位移传感器线扫描测量面形，lAB,2,θ、lAC,1,θ等以此类推；lAB,θ表示组合测量面为AB，测量线角度为θ的左右位移传感器线扫描测量面形之和，lAC,θ、lBC,θ以此类推。

(6) 对左右位移传感器线扫描测量面形之和lAB,θ、lAC,θ、lBC,θ进行最小二乘法直线拟合，依据直线斜率剔除左右平面光学元件测量面倾斜分量，公式(2)为

(2)

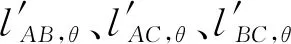
(7) 判断大口径平面光学元件测量面内各角度测量线是否都完成测量，如果完成则执行步骤8，否则回到步骤(4)继续执行。

(8) 判断AB、AC、BC3组测量面是否都完成面形测量，如果完成则执行步骤(9)，否则回到步骤(3)继续执行。

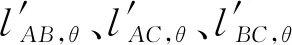
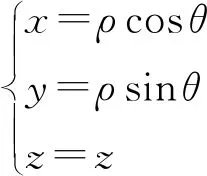
(3)

式中：ρ∈[-r,r]，r是大口径平面光学元件最大测量半径。

(10) 利用三面互检面形分离算法如公式(4)所示，对步骤(9)大口径平面光学元件组合测量面三维面形重构结果进行面形分离，得到大口径平面光学元件测量面A、B、C面形分布；

(4)

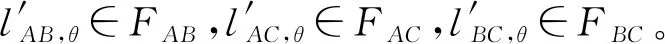
(11) 对步骤(10)所述三面互检面形分离结果A、B、C进行平面度评定[18,19]，计算PV值和均方根(root mean square， RMS)值。

理论上，基于反向共轴的大口径平面光学元件面形测量方法通过增加平面光学元件测量面上测量线条数，多次旋转组合测量，最后经面形分离可获得全面形分布，该方法最大测量口径取决于直线导轨的有效行程，量程主要取决于位移传感器的精度。

3 实 验

3.1 测量系统

为了验证本文测量方法的可行性，结合实验室现有条件搭建了大口径平面光学元件面形测量系统，见图4。系统主要由一对高精度激光干涉位移传感器及其位姿调整机构、精密气浮导轨、光学平晶位姿调整机构和旋转机构组成。系统主要参数如表1所示，该测量系统可以实现φ1 000 mm口径的平面光学元件面形测量，实验中对3块φ400 mm口径光学平晶进行面形测量。

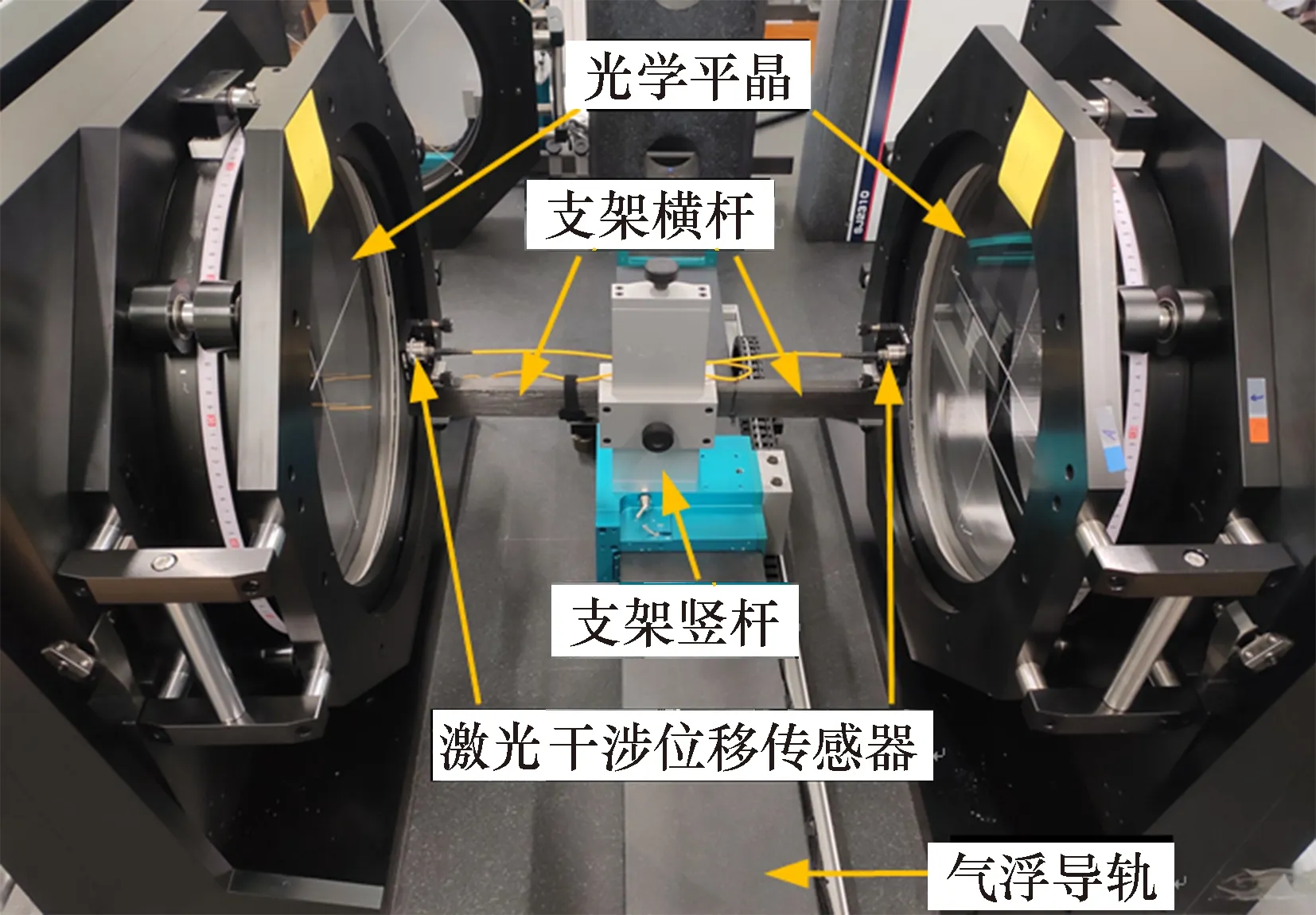
图4 测量系统图Fig.4 Measurement system diagram

表1 系统参数表Tab.1 System parameter

3.2 反向共轴位姿调整

在基于反向共轴的大口径平面光学元件面形测量之前，需要先调整左右激光干涉位移传感器反向共轴，位姿调整步骤如下：

(1) 左右激光干涉位移传感器沿直线长导轨扫描测量左右光学平晶测量面x方向中心线，分别计算左右光学平晶测量面x方向倾角，并借助光学平晶x方向位姿调整机构调整两光学平晶测量面与x方向平行。

(2) 利用光电自准值仪测量两光学平晶测量面y方向夹角，并借助光学平晶y方向位姿调整机构调整两光学平晶测量面平行。

(3) 利用可见光束从左侧光学平晶背面入射，经光学平晶折射垂直于测量面射出指向右侧光学平晶测量面，标记左右光学平晶测量面可见光斑位置。

(4) 利用传感器位姿调整机构，调整左右激光干涉位移传感器分别对准左右光学平晶测量面可见光斑标记点，且垂直于对应平晶测量面。

至此，两激光干涉位移传感器反向共轴位姿调整完成，测量过程中传感器位姿始终保持不变。

3.3 实验及结果

基于反向共轴的大口径平面光学元件面形测量实验按图3所示流程进行，先将光学平晶测量面A、B、C以45°等间隔划分4条测量线，接着以AB、AC、BC两两组合光学平晶测量面，组合光学平晶测量面上的测量线按角度依次对应并旋转至水平位置，反向共轴的左右激光干涉位移传感器同时进行线扫描测量。图5是组合测量面AB中0°线扫描测量结果(已剔除测量面倾斜分量)；对已剔除测量面倾斜分量的反向共轴线扫描测量结果进行三维面形重构如图6所示。

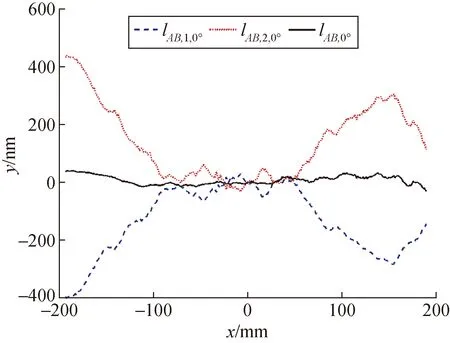
图5 反向共轴线扫描测量结果图Fig.5 Line-scanning measurement result of reverse coaxial mod diagram

从图5可以看出，由于导轨直线度误差存在单侧位移传感器线扫描测量结果lAB,1,0°和lAB,2,0°在500 nm范围内变化，而双位移传感器反向共轴线扫描测量结果lAB，0°在120 nm范围内变化，由此可见反向共轴线扫描测量模式能够有效抵消直线导轨在传感器测量方向的直线度分量。

图6(a)是对组合测量面AB各角度测量线按公式(3)重组的结果；图6(b)是用前20项zernike多项式对组合测量面AB中各角度测量线组合即图6(a)进行三维面形拟合的结果。

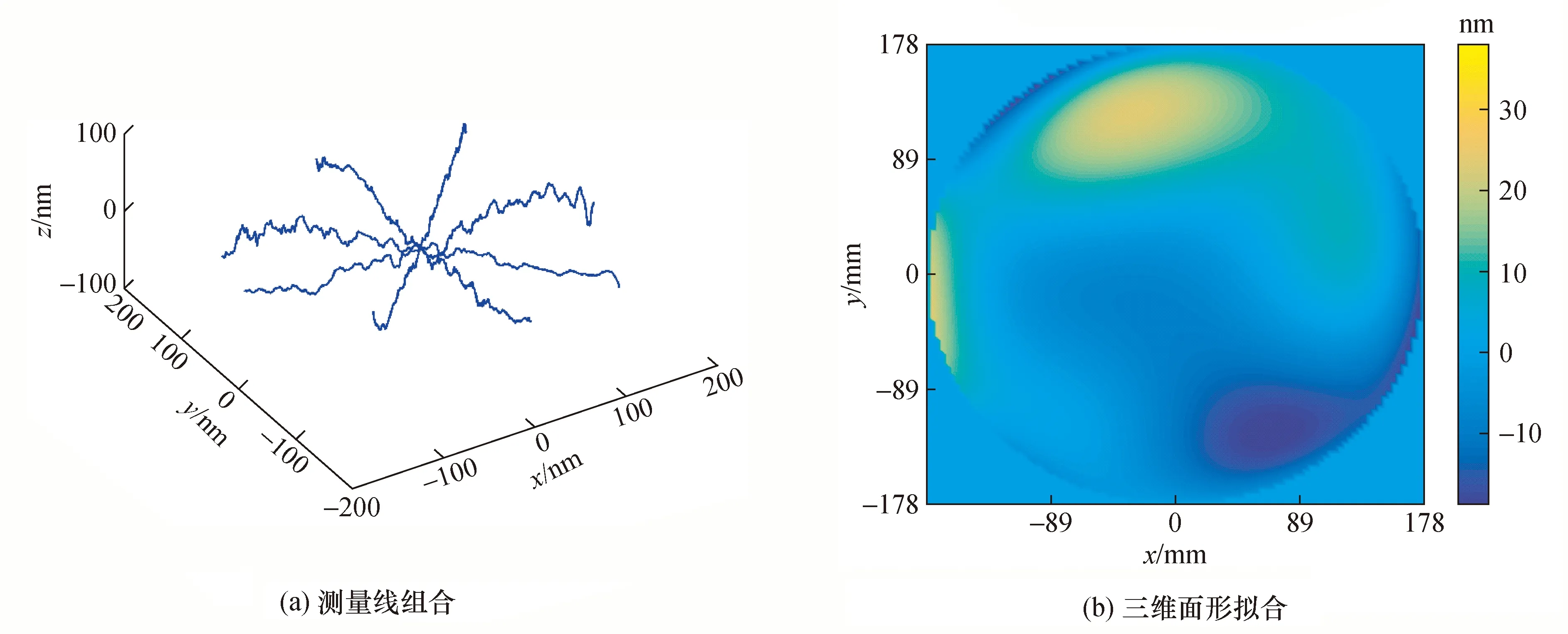
图6 三维面形重构图Fig.6 Reconstruction of 3D surface diagram

最后利用公式(4)三面互检分离得到A、B、C面形分布。3次实验面形分离结果如图7所示，纵向对比可以看出测量面A、B、C3次测量分离面形基本一致。

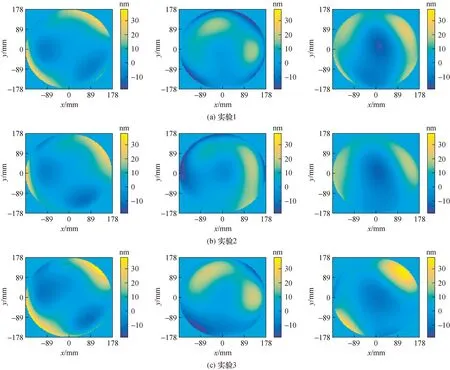
图7 3次实验面形分离结果Fig.7 Results of surface separation for 3 times experiments

3次实验面形分离结果用最小区域法平面度评定，PV值及其绝对误差如表2所示, RMS值及其绝对误差如表3所示。

表2和表3中测量面参考值由基于移相干涉技术的Zygo平面干涉仪相对法测量得到。面形分离结果和平面度评定结果验证了基于反向共轴的大口径平面光学元件面形测量方法的可行性。

表2 PV值及其绝对误差Tab.2 PV and its absolute error nm

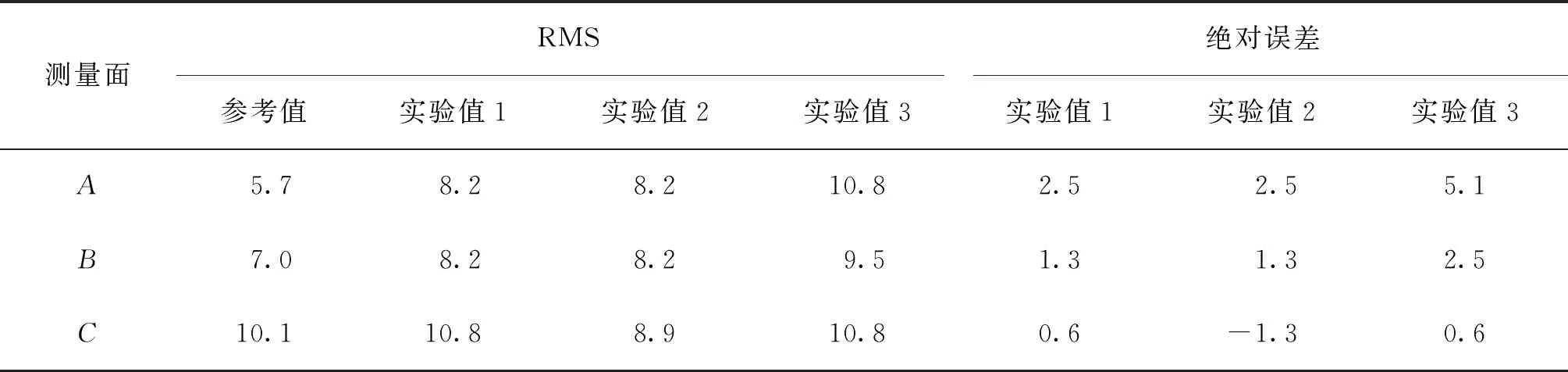
表3 RMS值及其绝对误差Tab.3 RMS and its absolute error nm

3.4 不确定度分析

由于基于反向共轴的大口径平面光学元件面形测量过程比较复杂，应用不确定度传播律时，计算模型的偏导数困难，故采用蒙特卡洛法(Monte Carlo method，MCM)评定测量不确定度[20，21]。基于反向共轴的大口径平面光学元件面形测量不确定度分析对象为光学平晶测量面实测PV值与真值的绝对误差，与面形PV值绝对误差相关的输入量有光学平晶测量面、测量口径、测量线条数、位移传感器参数、位移传感器倾斜、导轨参数、光学平晶旋转偏差、光学平晶测量中心偏移、光学平晶测量面倾斜、传感器支架竖杆高度和横杆长度、两位移传感器错位、导轨与平晶平面间距等，分析各输入量与面形PV值绝对误差之间的相互关系并建立系统测量模型，参考实际测量设置各输入量取值范围，见表4。表4中：N表示正态分布；U表示均匀分布。从各输入量取值范围中随机取值代入系统测量模型，计算面形PV值及其绝对误差。

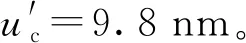
(5)

由式(5)可得到ucg=10.8 nm。

4 结 论

本文研究了一种基于反向共轴的大口径平面光学元件面形测量方法，将双位移传感器反向共轴线扫描测量模式和多角度旋转三面互检技术结合，对3块φ400 mm口径光学平晶进行了面形测量，通过实验验证了该测量方法的可行性， 并利用蒙特卡洛法评定了该方法的测量不确定度U=29.2 nm(k=2)，研究表明：

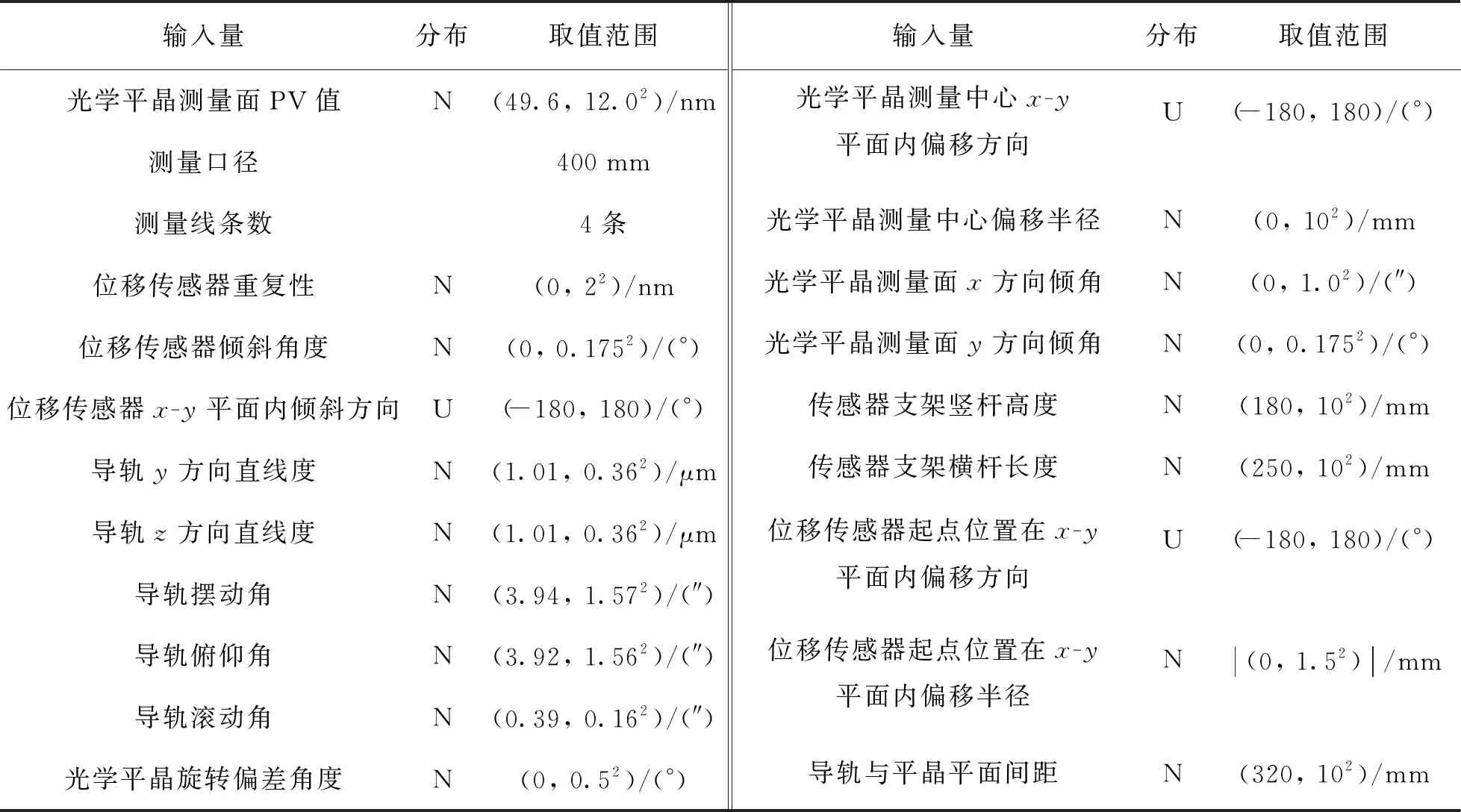
表4 各输入量的取值范围Tab.4 Value range of each input

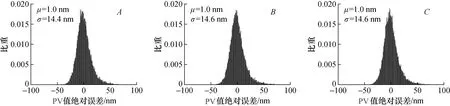
图8 基于蒙特卡洛法的仿真面形测量结果直方图Fig.8 Histogram of simulated flatness measurement results obtained by Monte Carlo method

(1) 该测量方法测量口径可达φ1 000 mm，测量口径主要取决于导轨有效行程，量程主要取决于位移传感器的精度；

(2) 该测量方法无需使用标准平晶，能够避免引入标准平晶参考面不确定度分量，将测量结果直接溯源到激光波长基准。

综上所述，研究成果对大口径平面光学元件的面形测量有重要参考价值与指导意义。