一种基于边指针搜索及区域划分的三角剖分算法
2021-03-04张俊田慧敏
张俊 田慧敏
三维重建技术是根据物体的二维图像信息恢复其三维模型,多年来一直是计算机图形学领域的研究热点[1−2].三角剖分是三维重建过程中最重要的基础之一,通过将散点连接形成许多互不相交的三角形或四面体,从而使模型面化或者体化[3].经过多年探索,研究者们对于二维三角剖分的研究已经取得了很多成果,提出了多种三角网格的优化准则和构造方法.其中,Delaunay 三角剖分由于具有良好的几何特性-可以最大化最小角[4],即能使得到的三角网格最平均,使用最广泛[5].然而,随着计算机图形学技术的发展,扫描设备的精度越来越高,用于三维重建的点集对象的规模也越来越大.因此,在保证三角网格的整体质量的提前下,有必要寻找一种更高效的Delaunay 三角剖分,从而满足三维重建的实时性.
Delaunay 三角剖分算法有很多种类,主要分为三大类:逐点插入算法[6]、分治算法[7]、三角网生长算法.其中,逐点插入法由于实现相对简单且占用空间相对较小[8],被大量研究者所采用;分治算法在执行时间方面可以达到最优,但占用内存较大,不适用于一般的计算机平台;三角网生长算法相对于前两种算法效率较低,不适用于大规模点集,在实际应用中很少被采用.逐点插入法的主要流程如下:1) 构造一个包含所有插入点的超级三角形;2) 将存储在链表中的点按序插入,遍历三角形链表找出包含插入点的三角形(即目标三角形),利用插入点将目标三角形拆分生成新的三角形,在三角形链表中删除目标三角形,完成一个点的插入;3) 利用空圆特性对新生成的三角形进行Delaunay 规则判断;4) 循环执行2) 和3),直至完成对所有插入点的处理.经典的逐点插入法有Bowyer 算法[9]、Watson 算法[10]以及Lawson 算法[11]等.
虽然逐点插入法易于实现,但在处理大规模的散点集数据时,实时性不是很好,为了提高逐点插入法的效率,研究者们进行了大量的研究.一部分研究者认为可以对插入点进行预处理,通过改进插入点的序列来提高三角剖分的效率.Liu 等[12]提出了一种基于广度优先搜索的确定性插入序列,使用k-d树来构造Delaunay 三角关系,但是构造k-d 较为复杂,需耗费大量时间.在多重网格插入法[13]的基础上,Su 等[14]提出了使用Hilbert 曲线遍历插入点,减少了三角剖分过程中狭长三角形出现的数量,从而降低局部优化时间.Zalik 等[15]提出一种两级均匀细分加速技术,将目标三角形问题转化为最近点问题,在他们的方案中,从最近的Delaunay 点开始,然后从第二个最近的Delaunay 点开始,以这种递归的方式直到找到目标三角形.在此基础上,Zadravec等[16]提出结合哈希表与跳跃表来寻找插入点的最近点,从而快速定位目标三角形.一些研究人员提出基于重心方向来定位目标三角形,但是,当出现分界点时,这种方法的搜索路径可能不唯一.针对此问题,Xi 等[17]提出可以通过移动重心来避免截点,从而使目标三角形可以连续搜索.随着计算机技术的快速发展,许多研究者们提出了并行Delaunay 三角剖分,将点集划分成许多独立的分区,这些分区可以同时进行Delaunay 三角剖分,Kohout 等[18]、Rong等[19]、Cuong 等[20]、Lo[21]均对此进行了研究及改进.此外,杨昊禹等[22]提出了并行动态Delaunay三角剖分算法,可以解决新增点位于原来三角网之外的情况.另外李国庆等[23]提出了基于凸多边形的Delaunay 三角剖分算法,使用生成的凸多边形代替传统算法中的超级三角形.常见的生成凸包算法有Graham 扫描法[24]、分区算法[25]等.刘斌等[26]提出将主成分分析法(PCA) 与二分法结合,通过快速确定凸包边缘点来计算平面点集的凸包.
通过对Delaunay 三角剖分逐点插入法的研究,可知在构建三角网过程中最耗时的部分为寻找插入点的目标三角形.本文在传统算法的基础上,将边指针与区域划分相结合,很大程度上提高了构建Delaunay 三角网的效率.
1 基于边指针的搜索
在传统的逐点插入法中,对每个插入点的目标三角形的搜索总是从三角形链表的表头开始.这意味着,目标三角形若位于链表的表头,则可以很快被找到;若位于链表的尾部,则需要遍历整个链表才能被找到.随着点的数量大幅度增加,三角形链表的长度也必然会大幅度增加,从而导致寻找目标三角形会越来越耗时,降低三角剖分的效率.针对此问题,本文对三角形的数据结构进行优化,提出了基于边指针的数据结构.如图1 所示,在△ABC中,A为起始顶点且A、B、C逆时针分布,AC为边1,AB为边2,BC为边3.在三条边上分别存在边指针P1、P2、P3,分别指向边指针所在的公共边的相邻三角形,如P1 指向与边AC相邻的三角形,对于P2、P3 情况类似.
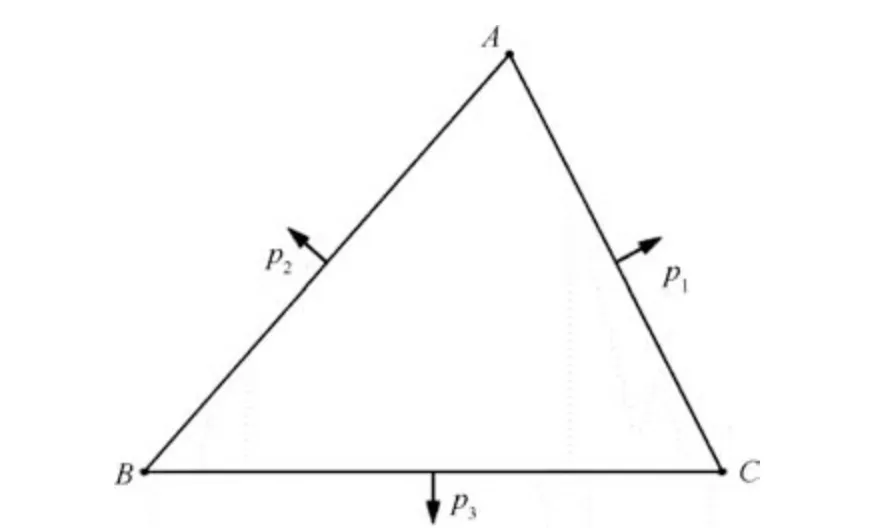
图1 三角形数据结构Fig.1 Data structure of triangle
1.1 点与三角形的位置判断
点与三角形之间的位置关系可以根据其坐标的相对关系来判断.对于任意三个点A(xA,yA),B(xB,yB),C(xC,yC),其中
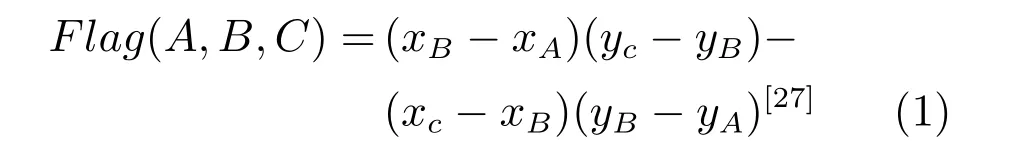
若Flag(A,B,C)>0,则A、B、C按逆时针方向分布;若Flag(A,B,C)<0,则A、B、C按顺时针方向分布;若Flag(A,B,C)=0,则A、B、C三点共线.如图2(a) 所示,若Flag(C,A,M)、Flag(A,B,M)、Flag(B,C,M)三者的值都大于零,则点M位于△ABC的内部.若三者中一个值为零且其余二者皆为正值,则位于某条边上,如图2(b) 中Flag(A,B,M) 为零,Flag(C,A,M)、Flag(B,C,M)为正值,故点M位于边AB上.若三者中至少有一个为负值,则点位于三角形的外部.如图2(c) 所示,Flag(A,B,M)为负值,故点M位于边AC的外侧.当然,点位于三角形外侧还会出现图2(d) 与图2(e) 的情况.在图2(d) 中,Flag(A,B,M)、Flag(B,C,M) 皆为负值,在此情况下,由于AB为边2,而BC为边3,本文中优先取编号在前的边,故认为M位于边AB的外侧.在图2(e) 中,点M虽位于三角形外部且与边AC共线,但是Flag(B,C,M) 为负值,故本文认为点M位于边BC的外侧.
1.2 基于边指针搜索的路径确定
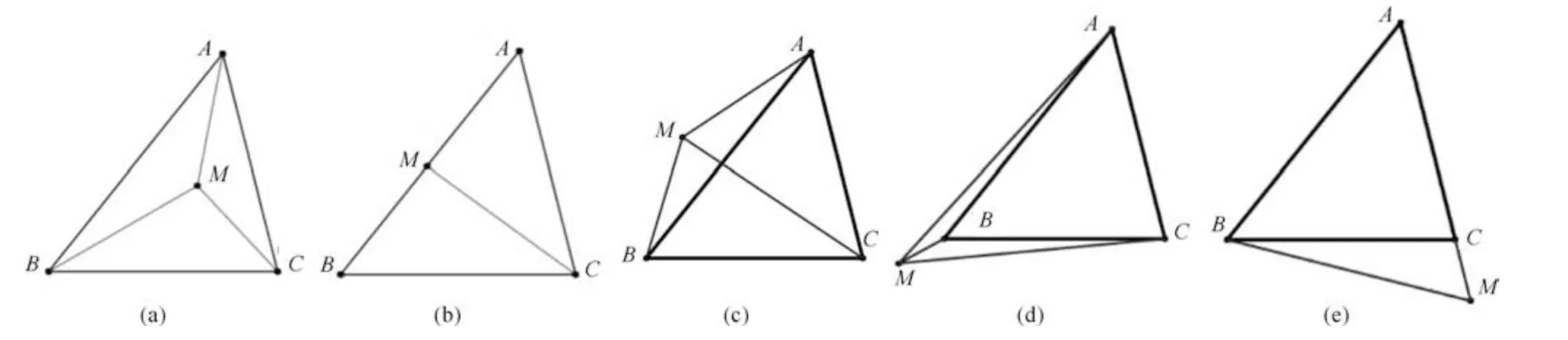
图2 点与三角形位置关系判断Fig.2 Judgment of positional relationship between point and triangle
在搜索目标三角形的过程中,搜索路径通过判断插入点与当前被搜索三角形的位置关系来确定的.如图3 所示,点V为插入点,假设△AIJ存储在三角形链表的表头,搜索过程如下所述.1) 检测点V与△AIJ的位置关系,首先确定了点V位于△AIJ的外部,然后确定点V位于△AIJ的哪条边的外侧,根据式(1) 可知点V位于边IJ外侧,故下一个被搜索的三角形为△AIJ的边IJ上的边指针p1所指的△IEJ.2) 用同样的方法确定接下来的被搜索三角形分别是△EFJ、△EHF,然后根据式(1)可知点V位于△EHF的内部,故△EHF为点V的目标三角形.在整个搜索过程中,共经过4 次搜索找到点V的目标三角形,搜索路径为:△AIJ(p1)→△IEJ(p2) →△EFJ(p3) →△EHF.边指针搜索的方式,由于在搜索目标三角形的过程中通过边指针的方向性可以快速地定位目标三角形,使搜索路径大大缩短,从而大大降低了三角剖分的耗时.
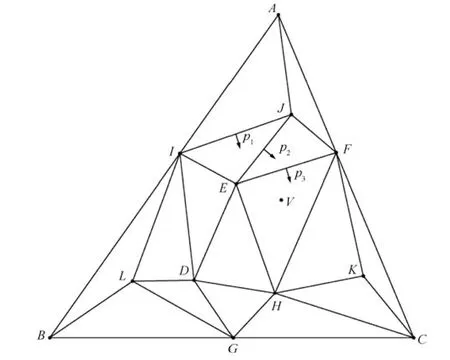
图3 点V 的目标三角形的搜索路径Fig.3 Search path for target triangle of point V
2 基于边指针搜索及区域划分的三角剖分
2.1 区域分块
基于边指针搜索目标三角形的方法,虽然可以利用插入点与三角形的位置关系来快速定位目标三角形,但是在点数量很大的情况下,目标三角形的搜索路径可能仍然会比较长,此时依旧较为耗时.因此,在边指针搜索的基础上,提出了区域划分的方案,以缩小目标三角形的搜索范围.
设区域分块为N × N,构造超级三角形的时候,首先遍历所有散点找到最大的纵横坐标值Xmax、Ymax,取两者中较大者得到max,然后根据max构造超级三角形,其各点坐标为:
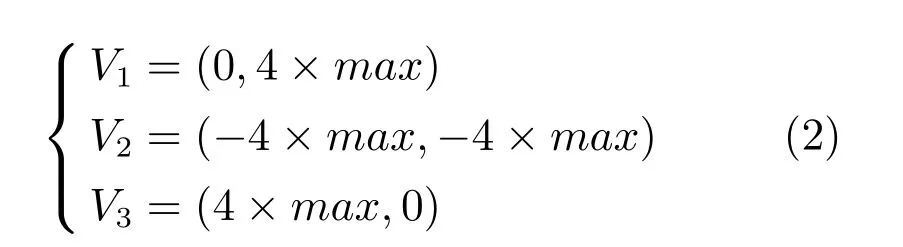
区域划分是指将包含超级三角形的正方形划分成N ×N个大小相同的区域,并将这些区域存储在二维数组中.每个区域的位置坐标值X和Y对应于其在二维数组中的存储位置,如位置坐标(1,2) 的区域块存储在数组area[1][2]中.对于插入点P(x,y),它的区域坐标由其本身的横纵坐标值确定:
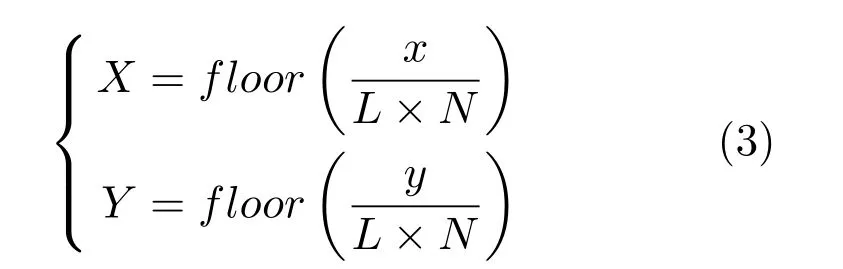
在式(3) 中,L指包含超级三角形的正方形的边长.
区域可以划分成不同的大小,对应的区域数量也会不同.对于某个确定的点集,如果区域太大,搜索范围会变大.但是,如果区域太小,则过多的区域很难被分配到入口三角形,从而导致入口三角形的使用率下降,进一步导致搜索目标三角形的时间增加.所以对于处理不同规模的点集,最优的分块也会不同.
对于点集V={V1,V2,···,Vn},两个点组成一条边,三条边组成一个三角形,三角形通过公共边上的边指针相互连接组成三角形网格.基于边指针搜索及区域划分的Delaunay 三角剖分的数据结构如表1 所示.

表1 基于边指针及区域划分的算法数据结构Table 1 Data structure of algorithm based on edge-pointer and region-division
数据结构包括4 部分:点、边、三角形和区域.每个顶点包含x和y坐标以及区域入口标志entryflag;连接顶点的边包含顶点Vi和Vj的编号;三角形采用空间网状结构,包含顶点Vi、Vj、Vk的编号,三角形的区域入口标志entry以及该区域的坐标X、Y,将位置相邻的三角形连接起来的边指针p1、p2、p3,区域坐标只有在entry=1 时才意义,如果entry=1,意味着三角形是该区域的入口三角形;区域块包含区域是否分配入口三角形的标志valid,以及区域的入口三角形指针对于一个入口三角形,在其三个顶点中存在一个入口顶点,其值被置为1,并且入口顶点位于于该三角形所记录的区域中.边指针搜索及区域划分数据结构中不同区域之间的关系如图4 所示,不同局域会分配一个入口三角形作为该区域的搜索入口,该入口三角形再通过边指针指向存在该区域内或其它区域内的相邻三角形.
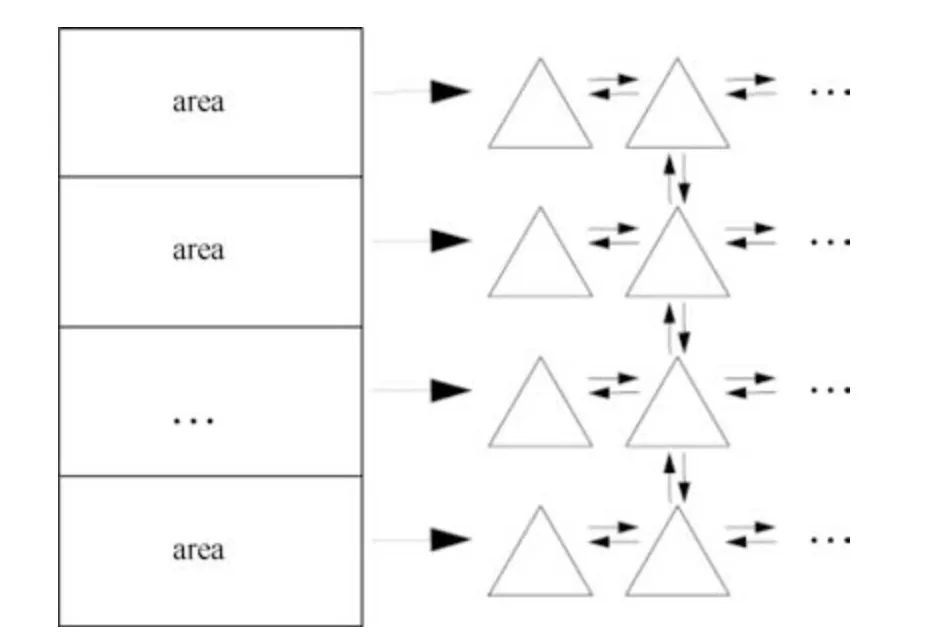
图4 结构体关系图Fig.4 Structure diagram
2.2 搜索目标三角形
实现Delaunay 三角剖分最重要也最耗时的部分就是搜索目标三角形,本文对目标三角形的搜索过程如算法1 所示.在基于边指针搜索的基础上,区域划分的搜索方式为每个区域分配了入口三角形.这使得对散点的目标三角形的搜索不是从三角形链表的表头开始,而是从入口三角形开始,故搜索的起始三角形更接近目标三角形,目标三角形的搜索路径进一步被简化.

图5 展示了基于边指针搜索及区域划分算法中搜索目标三角形的过程.如图5(a) 所示,包含超级三角形的正方形被划分成2×2 个区域.插入点V时,首先根据点V的坐标确定其所在区域为area[1][0].由于在点V之前,点H与点K已经被插入该区域,故该区域一定存在入口三角形,假设△GCH为入口三角形,对点V的目标三角形的搜索从△GCH开始.接下来,按照第1.2 节中所述边指针搜索的方式,确定目标三角形的搜索路径为:△GCH(p1) →△DGH(p2) →△EDH(p3) →△EHF,目标三角形为△EHF.
如果检测到点V位于三角形的某条边上,则需要根据边指针搜索另一个包含该点的一个三角形.如图5(b) 所示,点V位于边HF上,当找到△EHF之后,根据边HF上的边指针p4找到共边三角形△FHK.故△EHF与△FHK为点V的目标三角形,并且点V 将会被插入这两个三角形所构成的四边形内.
如果在点V所在区域中没有入口三角形,则从最新插入的点生成的三角形开始搜索目标三角形,搜索路径由边指针确定.由于该算法主要用于三维重建,而三维重建中扫描得到的连续点在位置上可能是相邻的,因此,由最新插入点生成的三角形可能更接近当前插入点的目标三角形.
在传统算法中,假设当前所有三角形按一下顺序存储在三角形链表中:△AIJ、△AJF、△IEJ、△EFJ、△IBL、△ILD、△IDE、△EDH、△EHF、△FHK、△CFK、△BGL、△DLG、△DGH、△GCH.插入散点V时,则需要依次判断链表中在△EHF之前的三角形是否包含点V,可以发现一共需要经过9 次搜索才能找到目标三角形,而本文的算法只需要经过4 次搜索就能找到目标三角形,搜索深度为传统算法的44.4%.随着点集的规模不断变大,传统算法的执行时间将会呈指数增长,本文算法的优越性会越来越明显.
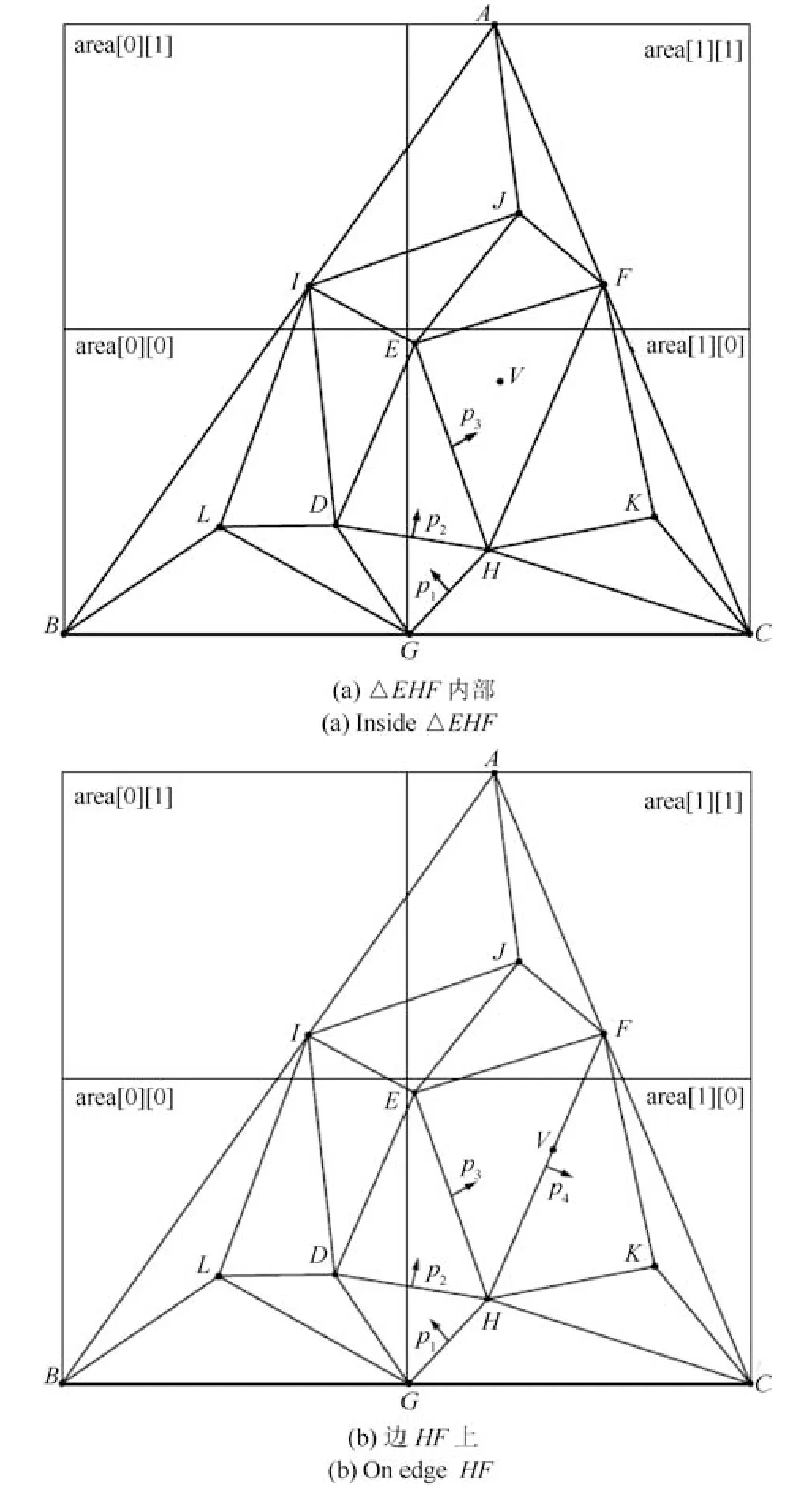
图5 搜索点V 的目标三角形Fig.5 Searching for target triangle of point V
目标三角形的定位是根据插入点与当前搜索三角形的位置关系来确定的,通过判断插入点位于三角形的哪条边的外侧来确定下一个被搜索的三角形.每一次被搜索的三角形都比上一次的三角形更接近插入点,因此通过这种方式一定能找到目标三角形,故该算法是收敛的.
2.3 区域入口三角形及边指针的更新
随着点地不断插入,区域的入口三角形也需要不断更新以确保其不会随着某些三角形的拆分而消失.同时,与新三角形有关的边指针也需要被更新以确保三角形之间能够互相找到相邻的三角形.找到目标三角形之后,需要将点插入到目标三角形中,并使用空圆特性对新生成的三角形进行Delaunay 规则判断及调整违背规则的三角形.在此过程中,需要更新入口三角形及边指针,入口三角形的更新分为本区域的更新以及他区域的更新.
如图6 所示,找到目标三角形△EHF之后,插入点V,生成了三个新的三角形(△EHV,△HFV与△FEV),并将原目标三角形△EHF从三角形链表中删掉.首先,对本区域的入口三角形进行更新.如果在此之前,区域area[1][0]没有分配到入口三角形,则选择△EHV为该区域的入口;如果area[1][0]之前已经分配了入口三角形如第2.2 节中所提到的△GCH,则△EHV代替△GCH作为该区域的新入口,并将点V指定为入口顶点.然后,根据被删除三角形的标志位及区域坐标信息检测其是否为其他区域的入口,若是,则需要指定一个新的三角形来更新此区域的入口.例如,如果三角形△EHF是区域area[1][1]的入口,判断△EHF的哪个顶点是入口顶点,根据点的入口标志位得出点F是入口顶点,因此,包含点F的△FEV成为了area[1][1]的新入口.
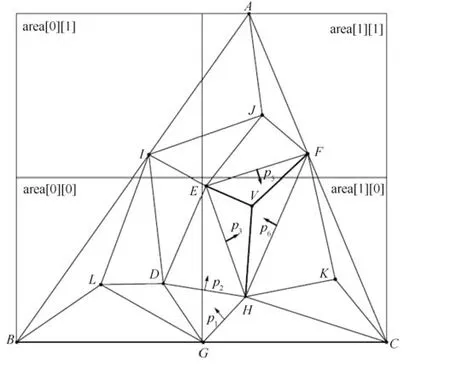
图6 入口三角形及边指针的更新Fig.6 Update of entry triangle and edge-pointer
此外,还需要更新和原三角形△EHF有关的边指针.在图6 中,随着△EHF的删除,原本指向该三角形的边指针应该指向新的三角形,△EDH的边EH上的边指针p3现在应该指向△EHV,同理,△EFJ的边EF上的边指针p5、△FHK的边FH上的边指针p6现在分别指向其相邻三角形△FEV、△HFV.
在进行Delaunay 规则判断的过程中,区域入口及边指针会以同样的方式更新,此处不再赘述.
3 实验结果及分析
为了验证基于边指针搜索及区域划分的三角剖分算法的效率,本文对随机生成的不同规模大小的点集进行三角剖分,并比较了传统的Delaunay 三角剖分(TD)、使用CGAL 库的三角剖分、基于边指针搜索的三角剖分(EPD)、基于边指针搜索和区域划分相结合的三角剖分(EPRDD) 几种算法之间的执行时间,此处的执行时间不包括读取插入点数据的时间.
在进行区域划分的时候,包含超级三角形的正方形被划分成了15×15 个区域.本实验的实验环境为Intel(R) Core(TM) CPU i5-8500 @ 3.00 GHz,16 GB 内存,Windows 10,VS2013,64 位操作系统,得到的结果如表2 所示:
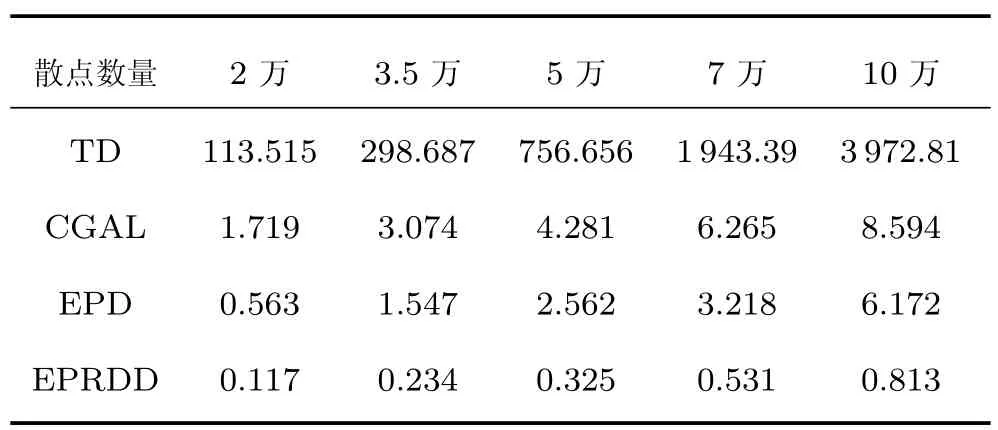
表2 算法的执行时间(s)Table 2 Running time of algorithms (s)
从表2 可以看出,当插入点的数量为2 万时,基于边指针搜索的三角剖分耗时为传统算法的1/201,加入区域划分之后,算法的执行时间为传统算法1/970.当插入点的数量为10 万时,基于边指针的搜索算法执行时间分别为传统算法的1/643,而基于边指针及区域划分算法的执行时间为传统算法的1/4 886.此外,与CGAL 算法相比,只使用边指针的算法优势并不是很明显;但是,边指针与区域划分相结合之后,算法的耗时明显低于CGAL 算法.当对10 万个点进行三角剖分的时候,CGAL 算法需要8.594 s,而基于边指针及区域划分的算法仅仅需要0.813 s 就能完成.
为了比较几种算法的执行时间与散点数量的关系,绘制了图7 所示折线图.由于传统算法的执行时间远远高于其余几种算法,故不与其他算法作比较.从图7 可以看出,随着散点数量的增多,CGAL算法,基于边指针搜索的算法与基于边指针搜索及区域划分算法的执行时间基本上都是呈线性增长的,CGAL 算法与基于边指针搜索的算法的执行时间随散点数量变化的增长速度还是较快,但是基于边指针及区域划分算法的执行时间的增长速度较为缓慢,斜率远远小于前两种算法.可以得知,随着插入点数量的增长,边指针搜索与区域划分结合的方法在时间上的优势将会越来越大.

图7 执行时间比较Fig.7 Comparison of run time
进一步对几种算法的平均搜索深度进行比较,结果如表3 所示.搜索深度是指在将散点插入到Delaunay 网格中的过程中搜索三角形的次数,搜索深度越小,三角剖分的实时性越好.由于CGAL 的源代码没有找到,在此处未对CGAL 的搜索深度进行比较.从表中可以看出,在传统算法中平均搜索深度与散点数目也是线性增长的,而基于边指针搜索及区域划分的算法的平均搜索深度很小.即使散点数量成倍增加,平均搜索深度也只是稍微增加,证明边指针与区域划分结合的算法实时性要高于传统Delaunay 三角剖分算法.其原因在于,区域划分缩小了目标三角形的搜索范围,边指针优化了搜索方向,最终使得搜索深度大大减小,执行时间得到降低.

表3 算法的平均搜索深度Table 3 Average search depth of algorithms
4 结论
为了满足三维重建的实时性,针对其基础部分三角剖分处理时间过长的问题,本文提出了一种基于边指针搜索及区域划分的Delaunay 三角剖分算法.在对传统Delaunay 三角剖分算法进行研究及实现的基础上,进一步优化了三角形存储的数据结构及搜索过程,设计了一种通过边指针反映三角形空间相邻关系的三角形数据结构来取代传统算法中的一维三角形链表.由于边指针具有方向性,可以用于确定距离插入点最近的相邻三角形,从而快速确定目标三角形的搜索方向.在此基础上将整个超级三角形进行区域划分,且随着散点的插入,每个区域将会分配一个区域入口三角形,作为搜索目标三角形的起始三角形,且入口三角形在构建Delaunay 三角网的过程中会不断更新.这使得目标三角形的搜索范围由以前的整个三角形链表缩小到插入点所在区域,从而进一步缩短搜索的起始三角形与目标三角形之间的距离,大大缩小了搜索范围,降低了搜索目标三角形的耗时,以满足三维重建的实时性需求.实验结果表明,该算法的执行时间随散点数量的增长较为缓慢,且散点数量为10 万时,所耗费的执行时间仅为0.813 s.
本文中的区域划分为固定划分,当散点分布密度变化大时,对于密度大的区域搜索深度可能会相应增加.为了进一步扩大算法的适用范围,后续研究中将引入自适应算法,寻求一种能够根据散点分布密度或者搜索深度的变化对区域划分方式进行调整的优化算法.
