一种基于双层框架的仿射类图像抠像方法
2021-03-04姚桂林赵志杰苏晓东辛海涛胡文秦相林
姚桂林 赵志杰 苏晓东 辛海涛 胡文 秦相林
数字图像的抠像与合成问题是在虚拟现实中图像处理领域的两种经典问题,目的是从一幅合成图像中将前景物体从背景中分离出来,并合成到一幅新背景图像中.对于合成问题,对于在数字图像I中的某个位置i=(x,y),给定前景图像的颜色Fi、背景图像颜色Bi以及一个透明度标量αi ∈[0,1],其观察到的颜色Ii能够用如下抠像公式表示为
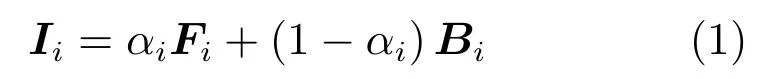
如果αi=0 或αi=1,将点i称作绝对前景或者绝对背景,并统称为绝对像素.对于其余0<αi <1的点,称为混合像素.
抠像问题为合成问题的逆问题,同时也是欠约束问题:给出各点的合成像素Ii,需要求出未知量Fi、Bi与αi.很多一般背景抠像问题都需要用户提供手工输入的辅助三分图Trimap,如图1(a) 和(b)所示,它包括已知绝对前景区域ΩF和已知绝对背景区域ΩB,剩余部分为未知区域.于是,依据已知像素,并根据抠像公式及某些先验条件,可以估计未知区域内的每个像素的{F,α}值.基于Trimap 的图像抠像算法通常分为如下2 种方式:1) 基于仿射的抠像方法[1−7].该方法并不孤立地计算每个点,而是考虑像素间的相关性,利用间接、迭代的方式递归地求出未知区域中各个点的α值.2) 基于采样的抠像方法[8−17].该方法对每个未知点独立从已知区域中选取样本,并采用逐对样本的计算方式,而并不考虑各个像素之间的联系.
本文主要讨论仿射类方法[18].虽然相比仿射类方法,采样类方法的采样位置和采样方式变化较多,而且获取样本方式非常直接,然而,仿射类方法具有以下优势.1) 仿射类方法充分强调了像素间的相关性,该方式也可视为由已知区域向未知区域缓慢、渐进的计算,因此在最终α结果的平滑性以及带给或用户的视觉感受上要明显好于采样类方法.2) 采用远距离搜索的仿射类方法对绝对点的计算效果较好,而在事实上,未知区域内的大多数点为绝对像素,因此该类方总体准确率上有较为明显的优势.本文在第1 节首先阐述了仿射类方法的2 种分类方式以及它们优点和缺点,在第2 节中针对KNN 类的特点讨论了绝对像素划分(即预处理) 方式,在第3 节中针对Matting Laplacian 类的特点讨论了剩余混合像素的计算,并在第4 节中讨论了这2 类方法各自的实验结果.最后第5、6 节讨论了仿射方法目前存在的问题并得出本文的结论.本文基于仿射方法的双层次抠像框架如图1 所示.需要说明的是,由于仿射类方法与采样类方法、乃至其他类如特殊类[19]、深度学习类[20−22]等方法采用完全不同的计算机制,而且本文主要研究前者,因此无论在理论研究和实验数据上,本文并未引入任何其他类方法,而且也不将结果传至α评估系统[23]中,以保持仿射类方法的整体一致性.
1 仿射类抠像方法概述
假设每个未知像素的α值是它的K邻域像素α值α1,α2,···,αK的线性组合,表示为
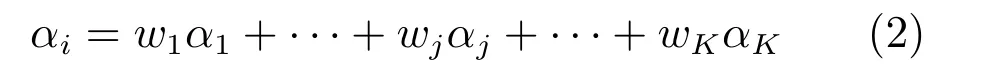
实际求解中,所有未知点i的αi可通过求解如下大型稀疏线性方程得到
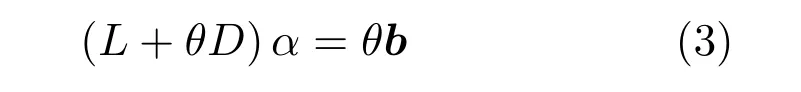
其中,L为长与宽均为图像像素总数的稀疏方阵,未知点i所在行对应K邻域的系数记为wj,j=1,···,K,D为对角阵,在已知点所对应的对角线元素的位置为1,未知点为0,θ为某个较大的数.b为长度等于像素总数的列向量,前景ΩF处位置为1,背景未知区域ΩU位置为0.上式可采用共轭梯度法求解.
1.1 仿射类方法的分类
各仿射类方法、亦即稀疏矩阵L的构造方式之间的主要区别是每个未知点i的若干近邻像素位置的远近以及相应权值wj的构造方式.按是否采用抠像公式以及在抠像中的实际效果,仿射类方法可分为不采用抠像公式的简单权重类方法以及采用抠像公式的Matting Laplacian 类方法.

图1 图像抠像问题的基本输入输出和本文的双层次抠像结构Fig.1 Input and output of image matting and the hierarchical framework of our method
1.1.1 简单权重类方法
该类方法如图2 左栏所示,其特点是不采用抠像公式,直接采用颜色差异的方法确定权重.具体的,当前点i与各近邻点j颜色差异的某个负函数即为各个权重,即与j的颜色越接近,权值越大,二者的α越相似.起初的Random Walk 算法[6]仅采用8 邻域处最近的搜索范围,但无论在绝对像素还是混合像素,其计算效果均很不理想.Nonlocal 算法[3]对邻域空间进行了扩展,采用以每个未知点为中心、半径为r的方形搜索寻找K个颜色最相近的点.为减少计算量,采样半径r通常不大.KNN 算法[4]的搜索距离则更远,需要寻找每个点在颜色约束和空间距离约束的特征下最近的K个点.
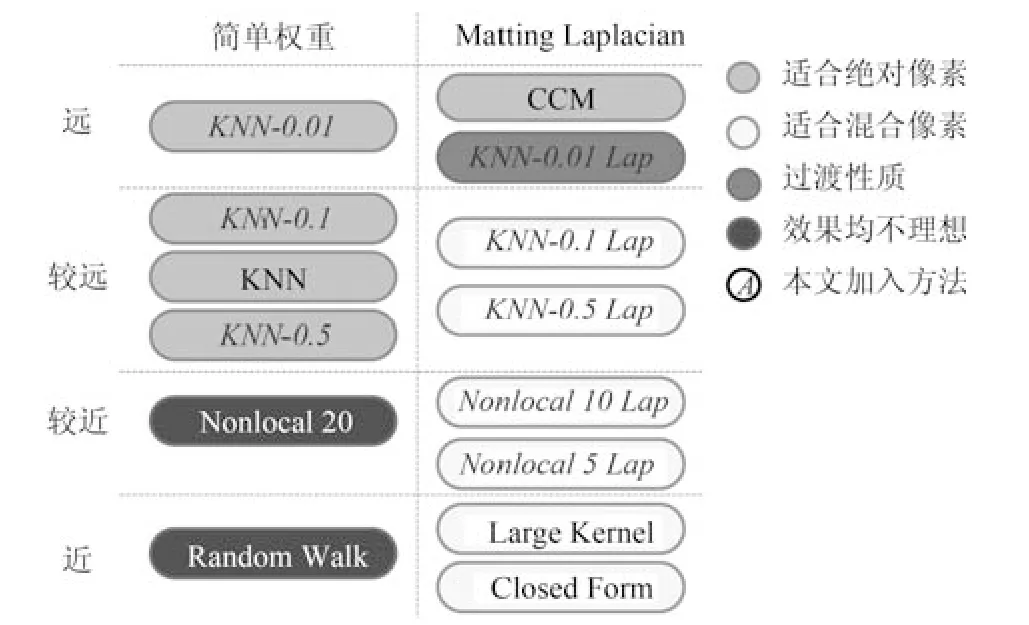
图2 仿射类方法的2 种分类方式对应的算法及适用范围(其中Lap 表明在原简单权重方法的基础上采用Matting Laplacian)Fig.2 Two types of affinity based matting method and the corresponding algorithms and application scopes(where Lap denotes the application of matting Laplacian based on simple weight methods)
根据式(2),若αi或其K个近邻像素的αj均接近于0 或1,即它们均为绝对前景或背景,此时的权值wj显然几乎无法构成影响.因此,在KNN 算法中讨论的权值是否采用exp(-x) 还是1-x的问题则显得不大重要.但若αi和αj为小数,即它们均为混合点,则权wj非常重要.然而,由于简单权重模式下的wj的产生并不采用抠像公式,而真实值αtrue是由抠像公式算出,因此此时的结果肯定不理想.由此可得出的结论是:该类方法适合于计算绝对像素,而不是混合像素.
另一方面,搜索范围较近的Random Walk 和Nonlocal 等方法,需要经过多次传递才能到达已知区域,因此较易造成误差累积.相反,搜索范围较广的KNN 算法可以通过较少次数的传递或直接搜索到达已知区域,会产生较少误差累积,更有利于绝对前景和背景的计算.这与采样类方法中直接访问已知区域的方式较为相似.
绝对像素计算步骤也同时在文献[24]中进行了深入讨论.据统计,在评估系统[23]提供的所有训练图像中,大型号与小型号Trimap 中的绝对点数量大大超过了混合点的数量,由此可以看出该步骤的重要性.进一步,该步骤必须单独采用一个独立的、不采用抠像公式的步骤,使其区别于普通的混合像素计算步骤,而简单权重类方法则完全符合这种绝对像素计算准则.目前,绝对像素的计算的算法仅出现在采样类计算方式中,但局部类方法[13−16,19]容易遗漏较远处的样本,误划分率偏高,而全局类方法[17]易受全局前景和背景颜色重叠影响,误划分率较高.由此可以看出,目前的绝对像素划分方法仍然受到全局与局部采样方式相互平衡的困扰.
1.1.2 Matting Laplacian 类方法
该类方法如图2 右栏所示,它假设在某“局部集合”S内,任何点i的前景和背景颜色Fi和Bi都是两个固定颜色{F1,F2} 和{B1,B2} 的线性组合,称为颜色线性模型(Color line model).结合抠像公式并经推导,结论为在某个集合S内的(i,j)∈S,点i与j产生的权重为
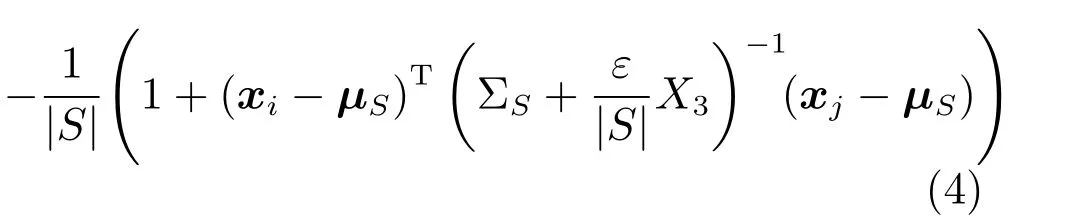
其中,xi与xj分别为点i与j的三维颜色向量,X3为3×3 单位阵,ΣS、µS分别为S内的3×3 协方差矩阵与3×1 的均值向量,ε为一个较小的数.未知点i与j的权重为所有包含二者的集合S所产生的权重之和.显然,由于采用了抠像公式,该类方法非常适合于混合点的计算,也是目前为止,仿射类方法中对混合点最重要的计算方式.
该类方法的关键问题是相关集合S如何选择.Closed-Form 算法[1]提出将集合S定义为较小的局部窗口,对于宽度较窄的前景硬边界效果较好,然而该类小窗口无法充分涵盖较宽的混合区域或前景空洞等实例的颜色信息.Large Kernel 算法[2]改进了基于空间局部窗口的思想,提出了核宽度r与不同未知局部区域的宽度成比例的方式.然而事实上,核宽度很大程度上依赖于真实混合区域的宽度信息,而未知区域仅为用户的粗略手工输入,尤其输入为稀疏的线条不能充分表达混合区域的实际信息,现实中还会存在很多偏差.CCM 算法[5]采用了KNN方式中的颜色近似的方法选取集合S,取代了空间方式的局部窗口.由于该方法搜索范围过大并引入大量已知样本,在实际中,它对绝对像素计算的效果较好,但对于混合像素的计算也受到全局绝对样本影响,出现过于二值化的现象.
CNN Matting 方法[20]提到,KNN 算法与Closed Form 算法之间的区别并不直接,由此采用基于深度学习方式对二者进行融合.然而经本文讨论至此,它们的区别已经非常明朗,即KNN 类方法适用于绝对像素的划分,而Matting Laplacian类(即Closed Form 类) 适用于混合像素的计算.本文从仿射类方法自身入手,据各类方法自身的优点和缺点做出相互的补充,避免了大量训练数据以及长时间训练等问题.
图3 显示了5 种典型算法在α评价系统[23]的52 幅训练图像上(27 幅训练图像中的大、小Trimap且不包含GT16),各αtrue区间的平均MSE 比较(不包含Random Walk),显然,KNN 在0~0.25与0.95~1 区间较好,印证了它非常擅长于绝对像素划分,而较为平滑的背景使得在绝对背景划分上更加优秀.CCM 仅在0~0.05 区间较好,说明它受前景和背景重叠的影响非常大.Closed Form 与Large Kernel 大致0.25~0.95 间较好,印证了它们擅长混合像素的计算.同时,近距离Nonlocal 算法在各区间中均不理想.
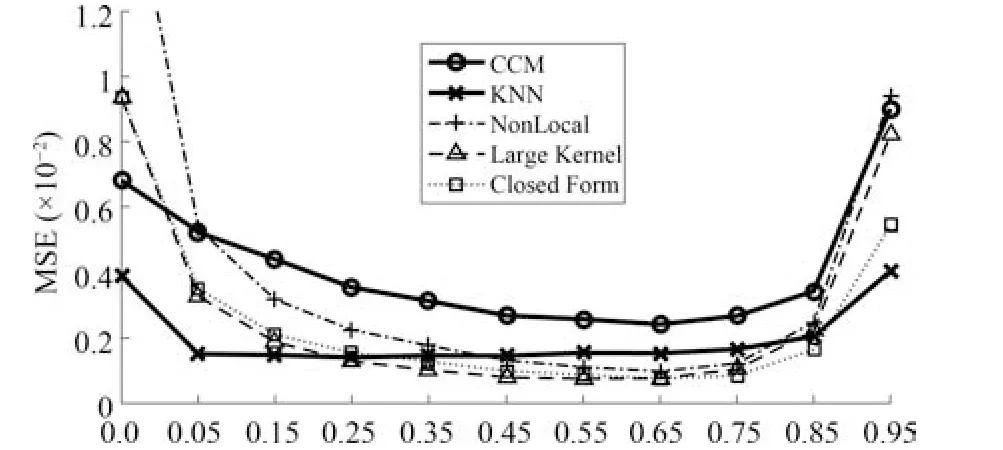
图3 各αtrue 区间中5 种传统仿射类算法α 结果的平均MSE 比较(其中x 轴坐标中的0.0 表示0.0~0.05 区间等)Fig.3 MSE comparison on five traditional affinity based matting algorithms in each αtrue interval (where 0.0 in x-label denotes the range of 0.0~0.05,etc)
1.2 本文方法的提出
事实上,KNN 类算法中K近邻像素的远近的选取,对该类方法的绝对像素划分结果会产生重要影响.在前景与背景的整体重合度不高的前提下,选择更远距离的搜索范围,不仅会为当前未知点提供更多相似的已知点,而且在Trimap 真实样本距离未知点较远时(如未知区域较大、或者前景存在空洞) 计算效果更好.但如果较远处的前景与背景颜色存在较大重合,则会产生计算错误,此时需要采用较小的搜索范围.因此,所选取的近邻像素的远近也是一个重要的平衡.然而,KNN 采用固定的远距离与近距离相结合的方式,无法根据空间上的颜色变化情况进行自适应调整.
基于上述分析,本文在第2 节新引入了KNN搜索上的3 种范围(如图2 左栏所示),并依据全局重叠与局部重叠程度,相应采用其中2 种层次相结合的方式,以期对大部分绝对像素进行划分,并进一步缩小未知区域的宽度.同时,由于无法保证初始Trimap 与混合点之间的关系,该层次采用与初始Trimap 未知区域大小无关的方式,这与Large Kernel 算法不同.
如前文所述,混合像素计算过程中的Matting Laplacian 类方法中的核宽度、或者搜索空间的大小,需要与真实未知区域的宽度相一致.若搜索范围过小则无法充分涵知区域的信息,造成CNN 算法[20]提到的“过平滑”,而搜索范围过大会导致混合像素的绝对像素化,如CCM.由于在第2 节中,相当多的绝对像素已被划分,且混合像素区域的大致轮廓也已确定,因此在此基础上,第3 节引入了KNN及Nonlocal 搜索上的5 种范围(如图2 右栏所示),并采用结合未知区域宽度的Matting Laplacian 方法,计算最终剩余混合像素.
2 绝对像素划分
本节讨论基于KNN 搜索方式的绝对像素划分.第2.1 节提出了搜索范围因子的概念,并定义3 种搜索范围下的直接点差异度,为后续章节打下基础;第2.2 节提出了图像重概念,将图像划分为低重合度图像和高重合度图像,前者按2.3 节计算α,后者按第2.4 节计算α.最后按第2.5 节的截取方式得到预处理后的Trimap.
2.1 搜索范围因子与直接点差异度
首先,类似于KNN 算法,定义像素i的特征矢量(f)=[ri,gi,bi,sxi(f),syi(f)]为i的3 个通道的颜色值,{ri,gi,bi} 为点i的空间距离特征,表述为
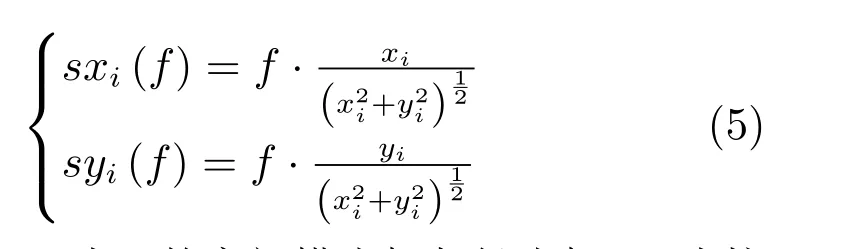
其中,xi和yi为i的空间横坐标与纵坐标,f为控制空间距离远近的重要参数.f越大,采集的像素越近,反之则越远.在KNN 算法中,f的取值为1 和0.01 之间的融合,其最终效果近似于0.5,如图2 所示.
前文曾提到,搜集像素位置的远近是KNN 类方法的决定因素之一,该问题非常依赖于前景与背景颜色的重合度.然而,传统的仿射类方法并不是直接访问已知区域的,直接获取每个点的前景和背景信息.因此,本文提出一种类似于采样方式的、直接访问已知区域的方法,用来模拟和引导每个未知点间接搜索距离的方式.这里需要利用FLANN (Fast library approximate nearest neighbors)方法,在相关特征xi(f) 下,靠近未知区域的5 个像素宽度的已知前景区域ΦF和背景区域ΦB位置(简记为F与B),对每个像素i分别寻找最近的前景和背景点j各K=10 个,将它们称为直接点,如图4(a) 下方的j点所示(以背景为例).在xi为xsi的前3 个空间无关特征分量、即颜色特征下,计算未知点i与上述前景与背景直接采样点对于K个直接点的平均颜色差异di(f,F) 与di(f,B),之后在给定距离参数f之下,计算点i的前景与背景颜色的差异系数:
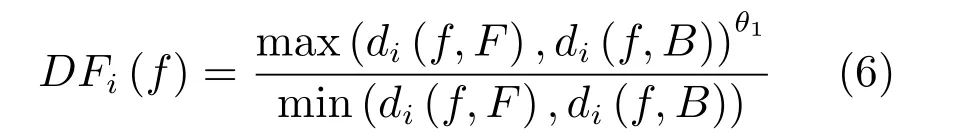
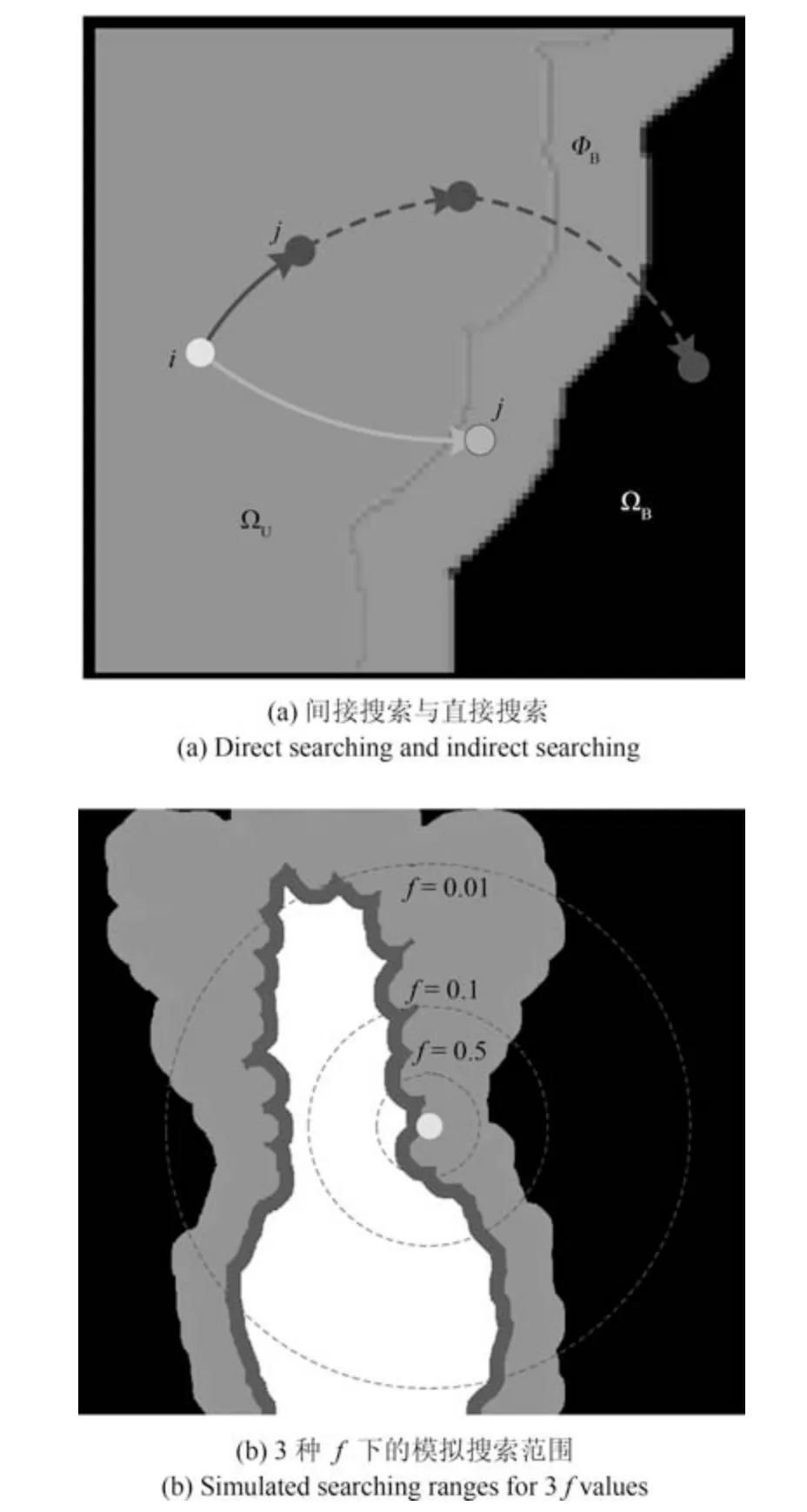
图4 以背景为例,未知点的各种搜索方式与搜索范围Fig.4 Various kinds of searching manners and searching ranges for an unknown pixel
其中,θ1的取值在1 至2 之间时,前景与背景的区分效果最好,这里取经验值θ1=1.5.DFi(f) 越高,表明在距离参数f下,点i的直接前景与背景颜色差异性越大,重合性越低,该距离参数f就比较理想;否则,该距离参数就不理想.
对每个未知点i,计算近、中、远3 个级别的差异度DFi(0.5),DFi(0.1)和DFi(0.01),并为后面的计算所采用.这3 个级别的近似搜索范围如图4(b)所示.
2.2 像素采集远近及图像的重合度判别
按文献[25]的理论,局部(或近距离) 采样方式应作为基本方式,而全局(或远距离) 采样方式是局部的一种补充.而这对于仿射类方法同样有效.考虑到各图像中前中前景与背景的重叠程度不尽相同,采集像素远与近的范围也不相同.首先,在未知区域ΩU内、靠近已知前景和背景区域的位置,分别定义1 个像素宽度为“学习区域”(简记为F与B),首先在距离参数f之下,计算这2 个区域到各自已知前景和背景的平均颜色差异dL(f,F) 与dL(f,B),
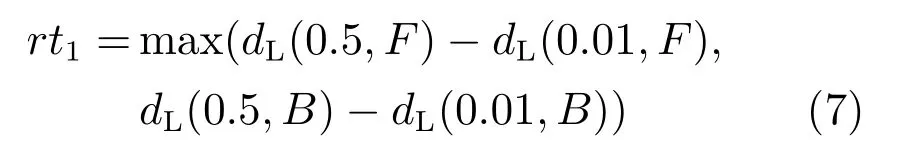
rt1越小表明近处像素点已经足够判别绝对像素点;否则,需要采集远处像素来实现.
其次,在特定集合M下定义如下准则:
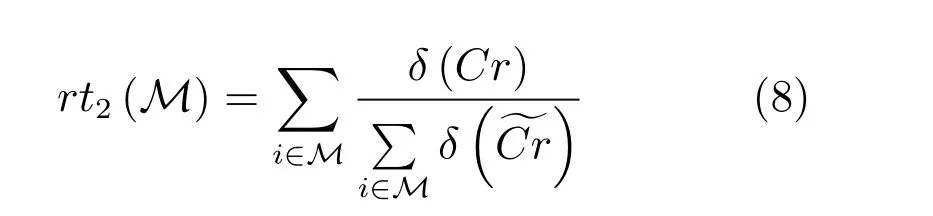
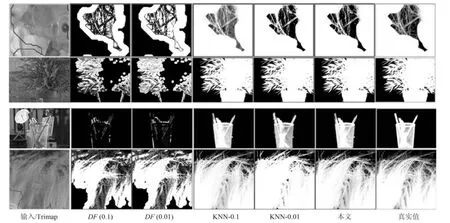
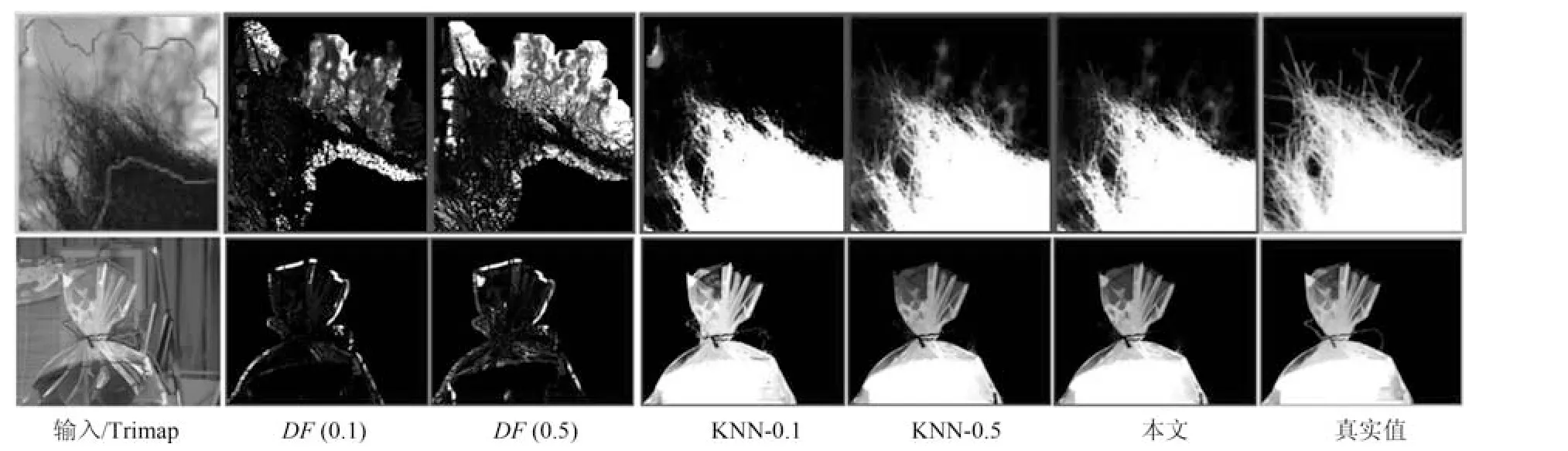
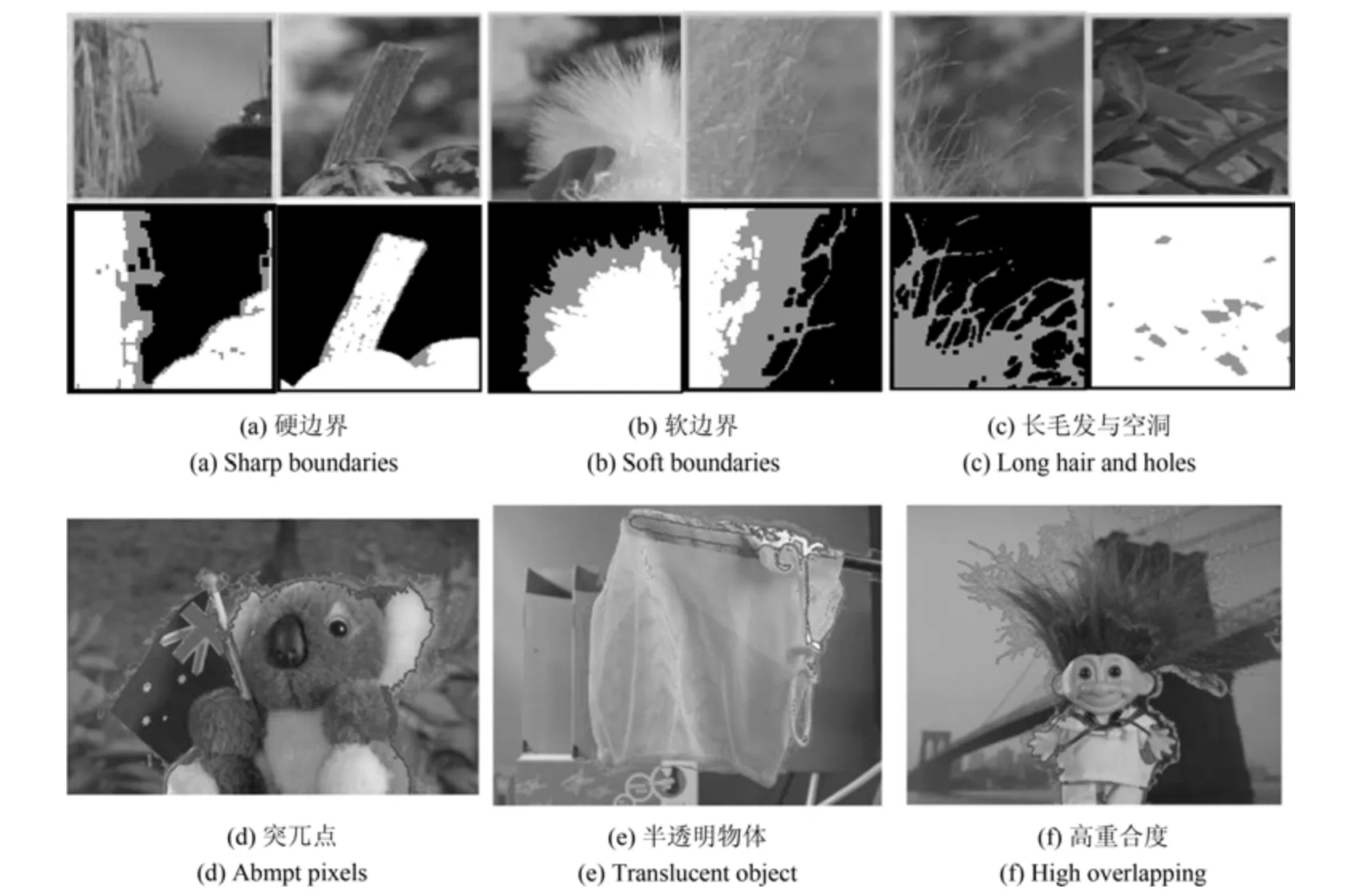
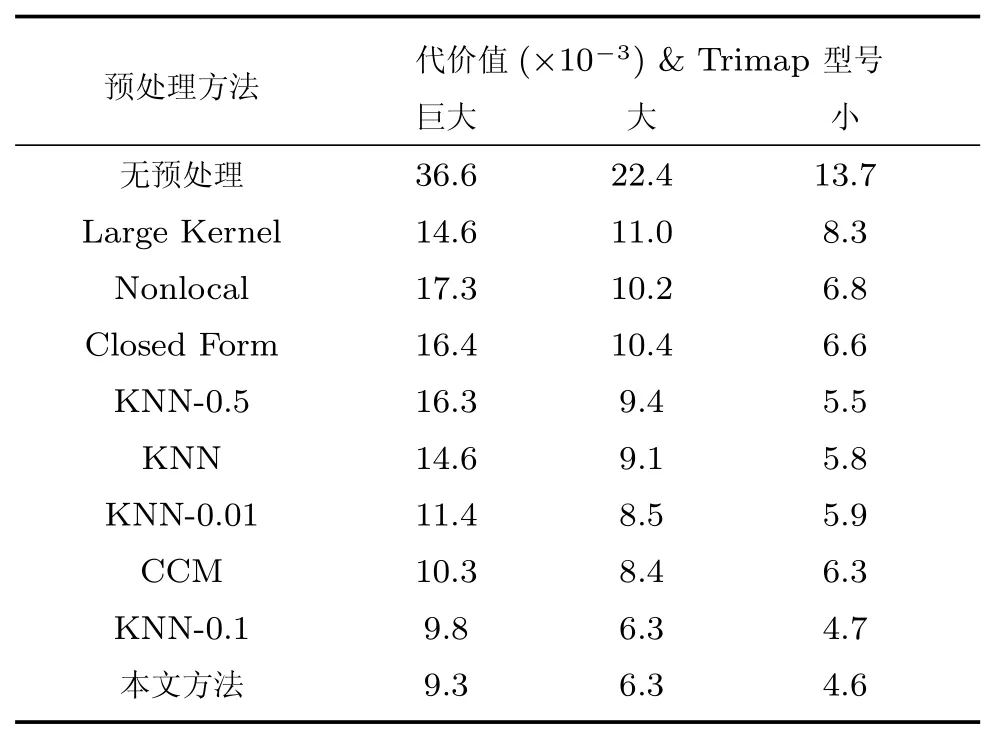
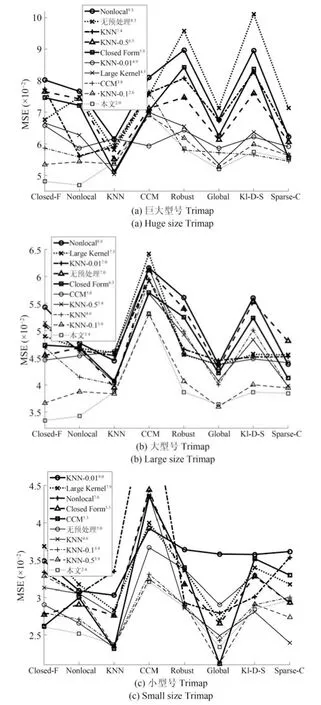
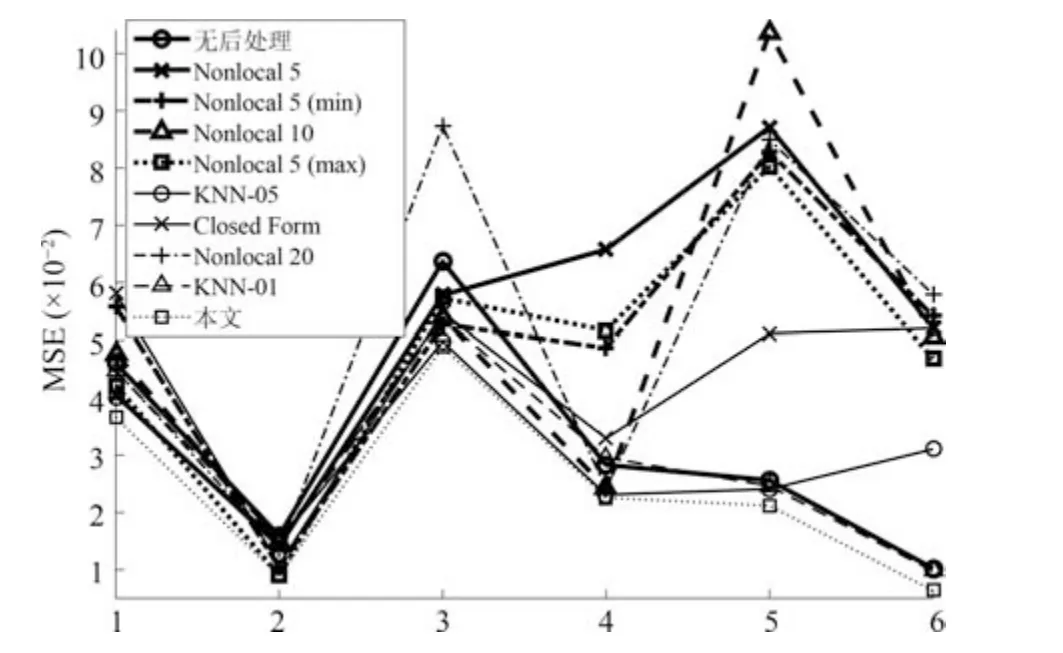
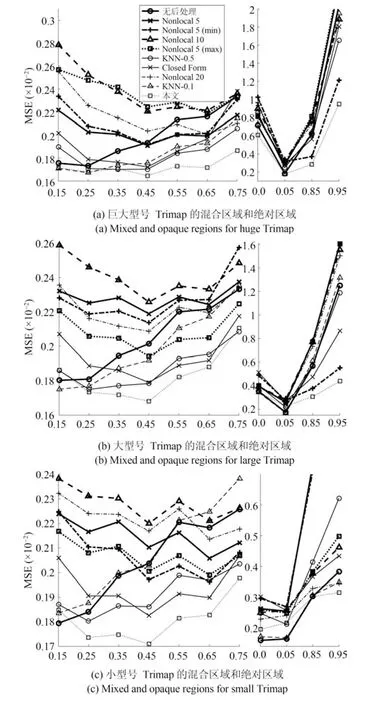
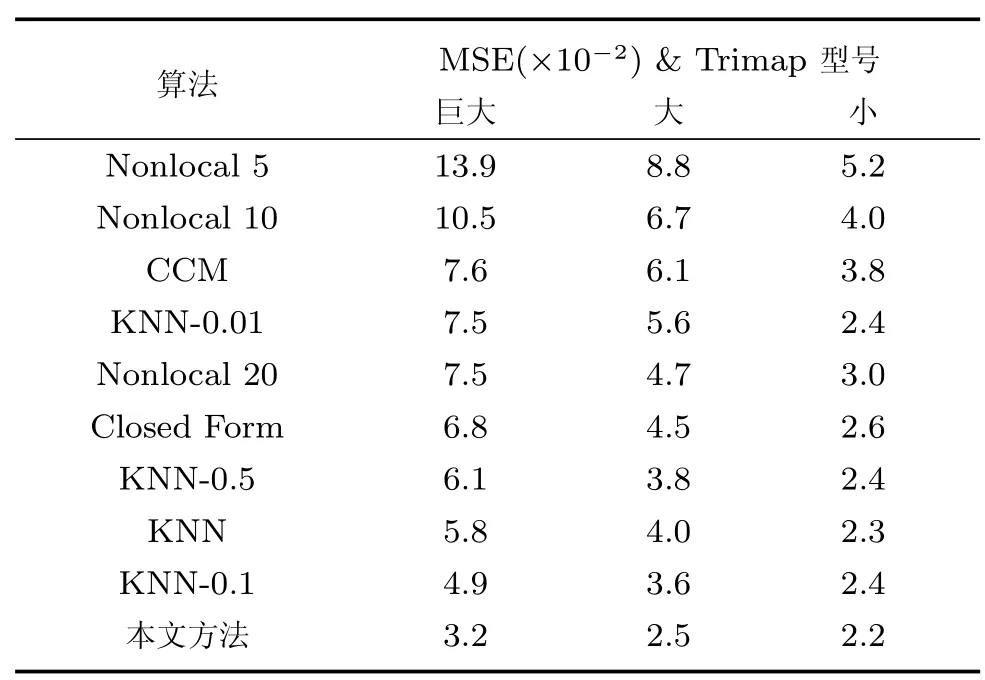
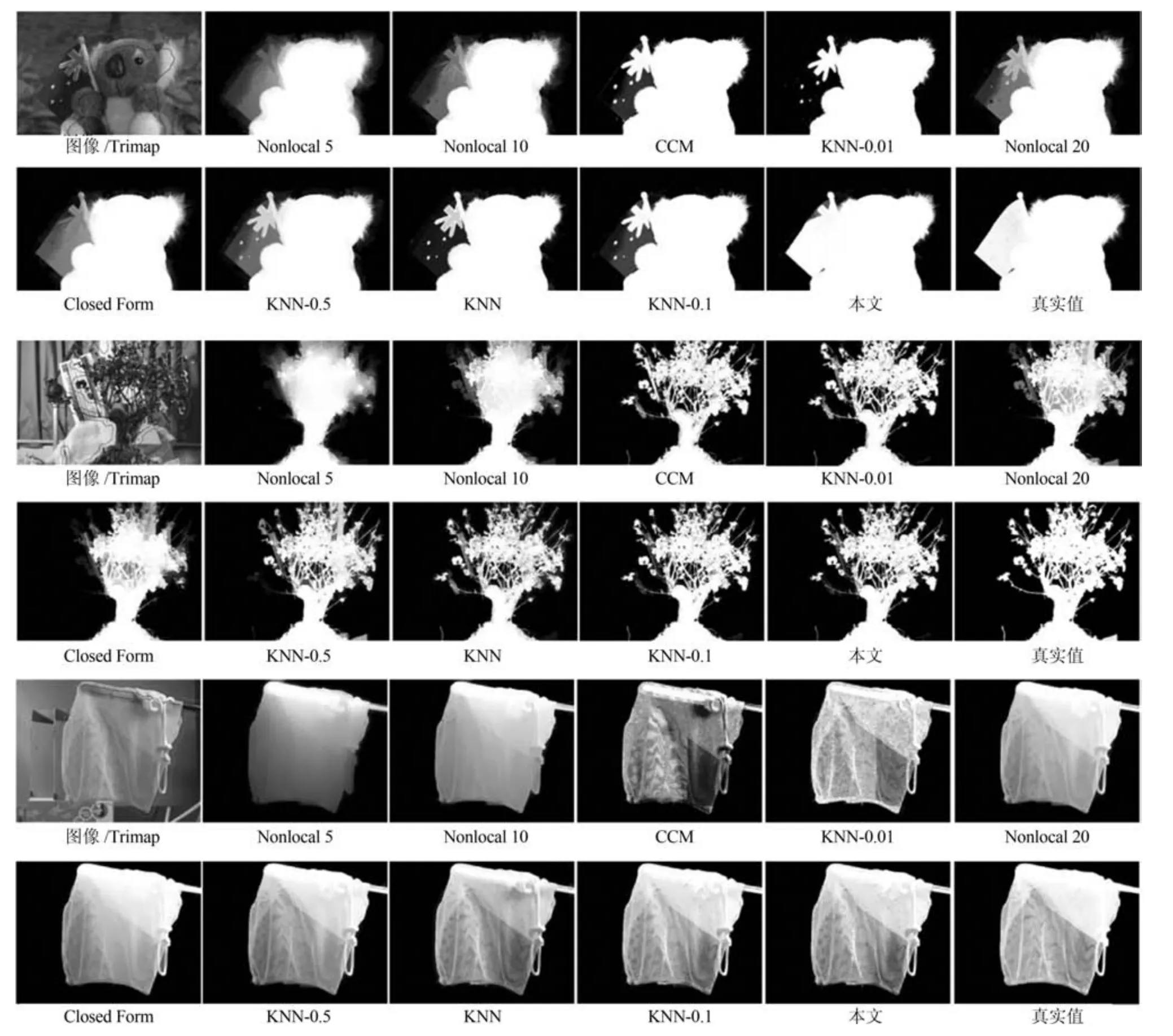
其中,判定条件Cr=(DFi(0.5) 其中,M1={i|i ∈ΩU∧DFi(0.1)<1},M2={i|i ∈ΩU∧DFi(0.1)≥1},θ2=0.7,θ3=0.4.之后,若T1≤0.7×10−4,则该图像为前景与背景重合度较高的图像;否则,若T1≥1.2×10−4,则该图为重合度较低的图像.若T1在上述二值之间,则进一步令T2=rt1·rt2(M1)θ2,若T2<0.8×10−4,则该图为重合度较高的图像,否则为重合度较低的图像.上述参数均根据经验取值. 最后,设定低度重合的图像采用2 个远距离级别的f为0.1 和0.01,而高度重合的图像采用2 个近距离的0.5 和0.1.每种重合度形式均采用近距离搜索范围为主、远距离为辅的搜索形式. 对每个未知点i,计算如下比例: 其中,di为在第2.1 节中求得的i与直接点颜色差异.定义如下f=0.01 处的判别准则 经第1 节分析可知,背景通常较为平滑,而前景变化相对较大,因此,若rti(F)>rti(B),则θ4=5,否则θ4=1.5,同时对上述情况均取θ5=1,上述参数取值表明对前景的约束要高一些.上式成立时表明:1) 该点在f=0.01 下与直接前景点或背景点的差异较在f=0.1 时小;2) 该点在f=0.01 下对应直接点的前景与背景之间差异较大.图5 的第2、3 列显示了DF的例子. 如前文所述,该方法需要利用直接点的前景与背景的重合程度,模拟KNN 类方法对间接点的采集远近.具体的,利用FLANN 方法,对每个未知点i在空间特征xsi(0.1)、xsi(0.01) 下,在ΩU处以及靠近它的40 个像素宽度的已知前景和背景区域位置(比直接点区域要宽),寻找与i最近的点j各K个,称为间接点,如图4(a) 上方的j点所示.于是,若满足式(11) 对应的约束条件,则未知点i选取远处f=0.01 的K个间接点,否则选取中距离处f=0.1 的.最后,对于像素i搜索到的K个像素,令它们同时对应了式(2) 中的K个位置,颜色特征为xj,则该类方法的对应式(2) 下的权值为wj=1-‖xi-xj‖/3.采用共轭梯度法求解所α值,记为αpre−our. 为了比较,本文也实现了单独运行的中距离搜索方法KNN-0.1 以及远距离搜索方法KNN-0.01.图5 同时显示了本文方法能够结合KNN-0.1 与KNN-0.01 的优点,并避免它们的缺点的例子(包括局部与全局图像).其中,前2 行显示了2 个前景存在空洞、且前景与背景差异相对较大的图像,此时第2、3 列显示了KNN-0.01 比KNN-0.1 在较多关键点中的DF要大,本文结果会利用这种优势来覆盖远处的已知背景像素,并避免在近距离搜索中容易遗漏的像素,使得更多已知点可以被划分出来.第3行显示了一幅前景与背景重合较大的全局图像,此时KNN-0.1 与KNN-0.01 的DF大都较小,而第4 行的局部图像显示了它们的DF仍然较为相似,此时对变化过大的前景像素进行过量采集时会产生“过搜索”.在这2 种情况下,本文方法采用相对保守的近距离搜索,避免了这些情况产生的误划分. 图5 全局低重合度图像中本文预处理方法与其他2 种单一搜索方式的结果比较(前2 列与后2 列分别显示了远距离与近距离搜索方法较好的例子,图像中的线条表示前景与背景边界)Fig.5 Comparison of pre-processing results between our method and two unary searching methods in low global overlapped cases (where the first and last two rows show good results in methods with long and short searching ranges respectively,and the lines in the input images show known foreground and background boundaries) 由于高重合度图像在直接点处前景与背景的重合度也较高,无法完全提供二者的准确信息,因此需要利用间接点的方式.类似于第2.3 节,首先,利用FLANN 方法,在上节定义的区域内对每个未知点i,在空间特征(0.5)、(0.1) 下,寻找最近的K个间接点j.之后在f下计算每个未知点i与K个间接点的平均差异,记为di(f),并定义如下f=0.1处的判别准则 其中,θ6=10,θ7=1,上述参数均根据经验取值.上式成立时表明:1) 该点在f=0.1 下与邻域间接点的差异较在f=0.5 时小很多;2) 该点f=0.1下对应直接点的前景与背景之间差异较大.于是,若满足式(12) 对应的约束条件,则未知点i选取较远处f=0.1 的K个间接像素,否则选取f=0.5 处的.求解αpre−our过程仍采用共轭梯度法.为了比较,我们也实现了单独运行的近距离方法KNN-0.5.图6 的2 个例子(包括局部和全局图像) 显示了前景与背景在远距离搜索KNN-0.1 上存在较大重合的图像,此时KNN-0.5 较KNN-0.1 在DF的很多像素上要大一些,本文则倾向于采用KNN-0.5 来避免这类重合所造成的计算错误.其中第2 个例子是测试图像,没有真实值,因此实际上我们引入了评价系统[23]上排名最高算法的结果图作为近似真实值. 最后,一种特例是该图所有未知点与前景和背景的颜色差异都较大,该例在正常计算时误差较大,此时该例完全简化为KNN-0.1,该平均颜色差异计算为 其中,直接像素差异di(0.01,O) 在第2.1 节定义,nU为未知点的个数,该约束条件为≥0.003. 图6 全局高重合度图像中本文预处理方法与其他2 种单一搜索方式的结果比较Fig.6 Comparison of pre-processing results between our method and two unary searching methods in high global overlapped cases 经之前的分析可知,KNN 类方法对绝对像素的计算较好,因此需要将αpre−our的绝对像素作为已解决的像素,并且将混合像素留给Matting Laplacian 方法计算.首先,对于未知像素i,成为新已知前景与新已知背景需要满足的条件为 图7 显示了经过前节得到的新Trimap 的6 个例子,可以明显看出,大部分绝对点都已被计算为已知点,而且剩余未知区域也可以基本描述出混合像素的分布情况,包括变化迅速的实心物体边缘(硬边界)、毛发式边界(软边界)、半透明物体等,这对于核宽度的选择或采用其他处理方式都是极大的帮助.同时,也很好地解决了Large Kernel 算法中提出的仅依据初始Trimap 中未知区域大小的缺陷. 依据前文的理论,混合像素的计算需要首先产生第1.2.2 节中的集合S,并利用Matting Laplacian 的方式生成权重.不同的是,本文并不采用Closed Form 和Large Kernel 算法中的基于空间连续的搜索方式,而是采用颜色特征相匹配的Nonlocal、KNN 及CCM 的搜索方式,该方式可以扩大搜索范围,并减少颜色线性模型带来的计算误差.这里每个未知点产生集合S的原则是:一方面,该集合要尽可能引入已知前景和背景区域,以消除在未知区域中传递次数过多而造成的累积误差,另一方面,获取的已知像素不能过多,以减少颜色过度重合造成的计算误差. 具体的,在新Trimap 下,首先计算每个未知点i与新已知前景和背景的最近空间距离,分别记为Di(F),Di(B),并求出二者的平均距离,记为Di,之后利用该参数调整Nonlocal 方法中的方形搜索半径r.进一步,若r较大,逐点方形搜索的方式所花开销太大,这时需采用KNN 或CCM 算法中的FLANN 方法.此时仍然遵循第2 节的多层次搜索原则,分为f=0.5、0.1、0.01 的3 级搜索方式.此外,本节依然采用与第2 节类似的、计算整幅图像重合度的方式,以此作为搜索范围的依据.在新Trimap 下,对每个未知点i获取经第2.1 节计算的3 个级别的差异度DFi(0.5)、DFi(0.1) 和DFi(0.01),按第2.2 节重新计算已知前景和背景的平均颜色差异dL(f,F) 与dL(f,B),并按式(9) 重新计算整幅图像的重叠度T1,若T1<2.0 则为高重合度图像,否则为低重合度图像. 根据每个未知点i与已知区域的空间距离,具体分为以下3 种常规情形,如图7(a)~(c) 所示: 1)“硬边界”,需要满足至少如下2 种情形之一.a)Di ≤8;b) 整幅图像是高重合度图像.2 个局部的例子如图7(a) 所示.此时对未知点i采用Nonlocal 的方形搜索方法,而搜索窗口要尽量覆盖到已知前景和已知背景区域,但也要避免窗口过宽.因此在半径为r下,按单纯的颜色特征x搜索K=10个与之最近邻的像素.半径r计算为 2)“软边界”,需要满足8≤Di <40.该情形代表较多毛发的边缘,2 个局部的例子如图7(b) 所示.类似于第2.4 节,利用FLANN 方法,在整幅图像中对每个未知点i,在f=0.5、f=0.1 时寻找最近的K个间接像素.并定义f=0.1 处的判别准则为DFi(0.1)≥0.1.若满足该约束条件,则未知点i选取较远处f=0.1 的K个间接像素,否则选取较近处f=0.5 的. 3) 长毛发边缘与前景空洞,需要满足Di ≥40,表明该点与已知背景距离很大,2 个局部的例子如图7(c) 所示.类似于第2.4 节,对i在f=0.1、f=0.01 时,寻找最近的K个间接像素,并定义f=0.01 处的判别准则为DFi(0.01)≥0.1,若满足该约束条件,则未知点i选取较远处f=0.01的K个间接像素,否则选取较近处f=0.1 的. 有时,整幅图像未知区域的空间距离或颜色差异较大,分为以下特例,如图7(d)~(f) 所示,此时以上常规方法并不奏效,需独立于上述情形之外单独考虑. 4) 存在大量与已知区域差异较大的点,或者所谓的“突兀点”,此时需要满足¯d >0.003,¯d为式(13) 定义的未知区域的平均颜色差异.一个全局的例子如图7(d) 所示,其中旗子部分与前景和背景的颜色差异都很大.此时在实践中将式(15) 中min 函数内的max 也同样变为min 可以使得最终抠像效果大为改善. 图7 预处理后的各种Trimap 情况Fig.7 Various kinds of Trimap after pre-processing 5) 存在大量半透明像素的前景物体,如塑料袋、网袋、杯子等.此时需要满足¯D >25,¯D为所有Di的平均值,且不满足条件4) 的情形.在大量像素需要远距离搜索的情况下,与CCM 类似,此时Matting Laplacian 会经常失效,又分为以下2 种情形:a) 该图为低重合度图像,一个全局的例子如图7(e) 所示.此时不做后续处理,直接采用预处理后的结果.b) 该图为高重合度图像,一个全局的例子如图7(f) 所示.此时意味着前面的预处理步骤很可能也不准确,这里直接采用KNN 算法下的HSV 色彩区间的结果. 最后,对于上述前4 种情形搜索到的K个像素,按第1.1.2 节形成Matting Laplacian 的集合S,并按式(4) 为像素i提供K个未知的权值贡献,采用共轭梯度法求出最终解αlap.要注意的是,此时式(3) 中的列向量b,对应所有已知点位置为其实际的α值,即新已知前景Ω′F处位置的范围为[αupper,1],新已知背景Ω′B处位置的范围为[0,αlower],其余未知点位置为0.求解中,若遇到共轭梯度法不收敛的情况,则直接采用预处理后的结果即可. 为了体现本文方法对于Trimap 大小的兼容性,对于评价系统[23]中的27 幅训练图像,除了大型号与小型号的Trimap 之外,我们另外为它们创建了“巨大”型号的Trimap,它们通过将大型号Trimap未知区域膨胀10 个像素、并保留面积小于500 的前景和背景区域得到. 本文选择了9 种仿射类的预处理方法,包括5 种已存在的算法(不包含Random Walk),3 种KNN 类算法KNN-0.5、KNN-0.1、KNN-0.01,以及本文方法.其中,Large Kernel 算法仅简单地将Matting Laplacian 的核宽度设为2,Nonlocal 算法的搜索半径为20,搜索10 个最相似的像素.对各方法中获得的α进行预处理方式均按式(14) 进行截取.为了比较预处理方法的有效性,未经预处理的方法也被引入. 4.1.1 预处理划分代价的比较 与传统意义上的预处理评价准则不同,由于在本文预处理步骤中的已知区域会引入一些半透明点,因此在某种划分下,将未知点i的代价函数定义为 表1 显示了上述10 种预处理方法(包含无预处理) 在3 种型号Trimap 下的总体代价比较,本文算法在各种不同型号的Trimap 下,划分代价均为10种预处理方法的最低.其他方法中,远距离方法(如CCM、KNN-0.01)在巨大型号Trimap 下代价较低,近距离搜索方法(如KNN-0.5)在小型号Trimap 下代价较低,过近距离搜索方法(如Nonlocal、Closed Form、Large Kernel) 在各种型号的Trimap 下代价均较高.搜索范围适中的KNN-0.1 各种代价也较低,而KNN 算法本身效果与KNN-0.5 较为相似. 表1 9 种预处理方法与未预处理方法在3 种型号Trimap之下对所有训练图像的代价值之和的比较Table 1 Comparison on sum cost of all the training images within 9 pre-processing methods and no pre-processing method over three types of Trimap 图8 显示了从图5 和图6 中获取的5 个局部图像,对它们采用10 种预处理方法(包含无预处理)的预划分代价.同样,本文算法的划分代价基本为10 种预处理方法的最低. 图8 9 种预处理方法与无预处理方法在一些局部图像中的代价比较(×10−4)Fig.8 Comparison on cost of several local images in 9 pre-processing methods and no pre-processing method (×10−4) 4.1.2 与后续抠像算法的联合比较 预处理方法不仅需要单独比较它们的漏划分和误划分率,同时注意到,预处理步骤和抠像步骤终究是一个整体,预处理步骤的成败需要最终的抠像结果反映出来,因此需要适当引入一些后续的抠像方法加以验证.本文选择了8 种典型的后续抠像算法,其中4 种仿射类算法(Closed Form、Nonlocal、KNN、CCM),3 种采样类算法(Robust、Global、KL-D-Sparse),1 种特殊算法(Sparse Coded).由于在预处理步骤中同时会引入一些半透明已知点,它们也会为后续抠像步骤产生作用,因此需要对这些抠像算法做出稍许改进.1)仿射类方法按第3 节方式初始化并求解;2) 采样类方法,假设每个未知点i的真实前景颜色Fi及背景颜色Bi与它的前景样本点j和背景样本点k的实际颜色相同,利用抠像式(1) 并推导可得 其中,Fj及Bk为前景和背景样本点实际显示的颜色,αj及αk为前景和背景样本点的α值.之后αi通过如下一般求解公式得到 3) Sparse Coded 算法,对于未知点i,设其字典D中p点的透明度值为αp,编码系数为βp,于是有 图9 显示了在巨型、大型、小型的Trimap 下10 种预处理方法针对上述8 种抠像算法的比较,因此每种型号下共有80 个结果,每个结果(即图9 中的每个点) 是由27 个训练图像结果的平均MSE 计算得到.显然,本文算法在各种不同型号的Trimap下,对8 种抠像算法的平均排名均位列10 种预处理方法的第一位,在每种单一抠像算法下的排名同样位居前列.与上节类似,远距离方法(CCM、KNN-0.01)、较近距离搜索方法(KNN-0.5) 分别在巨大型号和在小型号Trimap 下抠像效果较好,而过近距离搜索方法(Nonlocal、Closed Form、Large Kernel)在各种型号的Trimap 下的抠像效果都较差.搜索范围适中的KNN-0.1 排名也比较靠前,KNN 算法抠像效果与KNN-0.5 较为相似. 与上节不同,无预处理方法的排名并不在最后,说明一些预处理中误差过大的误划分对整体抠像结果影响非常大.而且,无预处理方法随着Trimap 未知区域的变小而效果变好,说明预处理的主要功能还是对于未知区域内的绝对点的划分.另一个有趣的现象是“自预处理”操作,即用一种算法本身进行截取,之后再采用该算法本身做出最终抠像.结果表明,这种方式并不能为该算法带来实质性的提升.例如图9(a) 中,若采用Closed Form 进行预处理并采用Closed Form 进行抠像,效果比单纯采用Closed Form 抠像要差.从而进一步说明预处理与抠像步骤进行分离、并采用不同方法的必要性. 图9 3 种型号的Trimap 下,对所有训练图像抠像结果的平均MSE 比较,格式为:算法名称排名,排名为在8 种后续抠像算法下,每种预处理方法在10 种预处理方法中的平均排名Fig.9 Average MSE Comparisons on the matting results of all the training images over three types of Trimap,where the format is [algorithm name]rank and the rank denotes the average rank for each of the pre-processing methods out of 10 over the 8 matting methods 在第4.1 节本文预处理结果的基础上,为了与本文混合像素的计算方法相比较,本文采用了其他8 种单一混合像素的计算方法,其中包括搜索半径5、10、20 的Nonlocal 方法,将式(15) 中min 函数分别采用min 和max 时的方法,KNN-0.5 和KNN-0.1 方法,以及Closed Form 方法(即Nonlocal 的搜索半径为1).另外,第4.1 节处理后的预处理结果(即第2 节中的αpre−our) 也被直接引入(记为无后处理).注意,这里各方法与第4.1 节的区别是它们均采用Matting Laplacian 取代了简单权重. 图10 显示了在图7(a)~(c) 中的6 个局部图像中采用上述10 种计算方法(包括无处理) 的MSE比较.显然无论在硬边界还是软边界,本文方法的计算效果均为最好.同时注意并未采用Matting Laplacian 的无预处理方法,该结果虽然也较为不错,但相比上述方法中的一些结果要差,这验证了前文提出的需要进一步引入Matting Laplacian 进行混合像素计算的基本理论.在其他方法中,对于未知区域很窄的第1、2 个例子,Closed Form、半径为5的Nonlocal 等近距离方法尚且不错,但在第3、4 个例子中随着未知区域的扩大,一些半径为10、20 的Nonlocal 方法变好,而至最后未知区域非常宽的第5、6 例子时,固定搜索半径的方法已基本失效.然而,由于KNN-0.5 及KNN-0.1 的搜索范围并不完全受距离因子的局限,可以根据颜色变化情况,灵活和动态选择较远处的像素,因此它们的效果始终较好. 图10 对于图7 的前6 个局部图像及预处理后的Trimap,采用10 种方法进行抠像计算后的MSE 比较,其中前2 个例子为硬边界,中间2 个例子为软边界,后2 个例子为长毛发边缘与前景空洞,且这些例子中未知区域的宽度也逐渐增大Fig.10 MSE comparison on matting results of the first 6 local images in Fig.7 for 10 matting methods,where the first,median,and last 2 cases are hard boundaries,soft boundaries,and long hair edges and foreground holes respectively,in which the sizes of unknown regions gradually enlarge 为了显示本文方法的综合计算能力,与上节类似,上述10 种方法在3 种型号Trimap 下的27 幅训练图像的α结果的平均MSE 比较均显示在图11 中.同时,为了显示α结果分别对于绝对像素和混合像素的处理能力,与图3 类似,将各αtrue划分为若干均匀区间,并将绝对像素区间(0~0.15、0.85~1)与混合像素区间(0.15~0.85)分别显示. 图11 3 种型号的Trimap 下,在各α 区间上,10 种混合像素计算方法对所有训练图像的抠像结果的平均MSE 比较,其中x 坐标轴中的0.15 表示0.15~0.25 区间等Fig.11 Average MSE comparisons on matting results of all the training images for 10 matting methods over 3 types of Trimap in each α range,where 0.15 in x-label denotes the range of 0.15~0.25,etc. 显然,相对其他处理方法,本文方法除了在混合像素上计算精确外,对剩余绝对像素的计算仍然具有明显优势.在其他方法中,由于大宽度未知区域的例子偏多,且占据误差计算的主导地位,因此固定搜索宽度的Nonlocal 方法始终不理想,而搜索范围相对灵活的KNN-0.5 及KNN-0.1 方法则要好很多.一个特殊的例子是搜索半径为1、且效果同样不错的Closed Form 方法,此时仍然可以理解为Matting Laplacian 在较小范围内更为有效,因此搜索范围的远近也是一个微妙的平衡. 最后,我们将本文中的绝对像素划分步骤与混合像素计算步骤合并为一个整体算法,并与9 种已经出现的仿射类算法(或变形) 做出比较.其中采用简单权重方法的有:搜索半径20、10、5 的Nonlocal 方法,KNN-0.01、KNN-0.1、KNN-0.5、KNN方法;采用Matting Laplacian 方法的有:CCM 和Closed Form 方法.需要注意的是,上述单层次方法是可以与本文双层次方法相比较的,主要由于这些单层次的方法也可以视为双层方法,即首先对自身做预处理(先运行一次该算法并做出α ≥0.95 和α ≤0.05 的绝对像素划分)、再用自身做后处理(在预处理基础上再运行一次该算法).如前文所述,这些算法按双层次方法运行2 次,和只运行该算法一次的效果相近,因此可以用一次运行的上述算法模拟2 层次运行结果. 表2 显示了上述10 种方法在3 种型号的Trimap 下的平均MSE 总体排名和分别排名,本文方法对整体和各Trimap 型号的效果均为最优. 表2 10 种仿射类方法最终抠像结果的MSE 比较Table 2 Final MSE comparison on matting results for 10 affinity based matting methods 图12 10 种仿射类抠像方法的3 个实例Fig.12 3 Cases of matting results for 10 affinity based matting methods 图12 显示了各算法对于抠像效果的视觉比较,其中前2 个例子(前4 行) 显示了2 幅训练图像.其中第一幅来自于图7(d),国旗部分与前景和背景部分的颜色差异均非常大,而第2 幅的前景与Trimap的形状均非常复杂.本文方法对这2 个例子均能处理的非常好.第3 个例子(后2 行) 显示了1 幅测试图像,它们经第一步预处理后的未知区域仍然非常大,且无法通过普通Matting Laplacian 计算得到,本文方法能够获得最好的结果. 1) 离散与连续的KNN 类搜索方式.本文对KNN 类算法中的3 种由远及近的搜索范围因子0.01、0.1、0.05,是3 种离散化的初级方式.而如何根据前景背景的重合情况,采用连续函数方式进行搜索,需要后续工作的进一步研究. 2) 简单权重与Matting Laplacian 的适用范围.如图2 所示,简单权重方法较适用在中远距离范围,而Matting Laplacian 方法较适用在中近距离搜索范围,但在二者的共同区域、即中距离或偏远的范围上,应采用何种权重的计算方式仍显得非常模糊,例如KNN-0.01、KNN-0.1、Nonlocal 20 等方法,对于它们确切的应用范围仍需要进一步实验来验证. 3) 初始Trimap 未知区域大小的问题.介于本文在第一步预处理中对于Trimap 输入无关的设计模式,并未考虑初始Trimap 未知区域的形状和大小,这对于未知区域较宽的实例非常有效.然而事实上,当初始Trimap 的未知区域非常小时(如评价系统中的小号Trimap),也可以适当考虑采用更加保守的搜索方式以减少误划分,这种方式的抠像结果需要进一步实验验证. 4) 仿射类方法的局限性.尽管本文在预处理步骤中采用了直接像素,然而采样类方法的迭代最终需要间接的方式求解,与采样类方法相比,仍然缺乏前景和背景的直接信息,在某些场合中容易造成间接误差的累积,而且无法像采样类方法在算法结束后对单个点进行观察与调试,若效果不佳,只能尝试改进一些算法参数,并重新运行整个程序,这也影响到了该类算法的后续分析和改进.因此类似于后处理方法[26−28],本文方法仍然可以与采样方法结合. 5) 对于大规模图像和视频数据的抠像应用,算法效率非常重要,今后的工作将考虑采用多核CPU、众核GPU 等并行技术[29−30]来加速所提出的算法,以便处理大数据量的图像和视频. 本文采用了“绝对像素划分―混合像素计算”的双层次计算方式求解仿射类图像抠像问题.其中,第一层预处理步骤采用了基于KNN 类简单权重的多种搜索距离的联合方式,第二层后续抠像步骤采用了基于Matting Laplacian 的多种搜索距离的联合方式,以充分发挥这两种传统抠像方法的特点.同时,本文针对全局与局部前景与背景的重合度,相应采用不同的搜索层次,并采用了以局部近距离搜索为基础、全局搜索为补充的策略.在实验中,本文同时引入了若干中间层次的抠像方法与本文方法进行比较,以验证本文方法对上述2 个层次的抠像结果的有效性.最后,本文对后续探索方向进行了展望,以推进下一步的工作. 致谢 感谢赵世杰教授、徐耀群教授和白世贞教授在本文写作过程中的支持和帮助.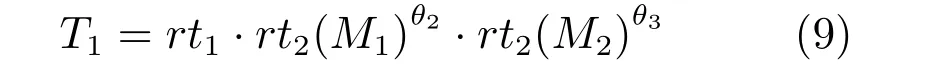
2.3 低重合度图像
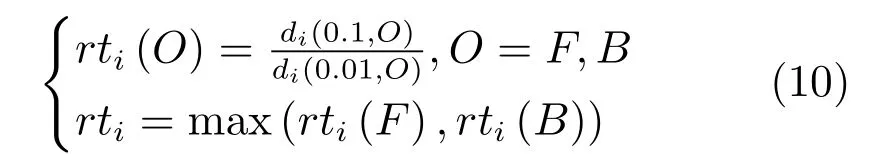
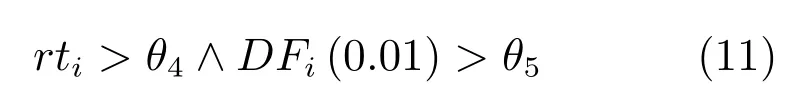
2.4 高重合度图像

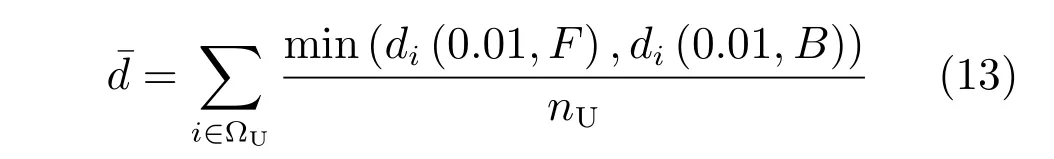
2.5 Trimap 的更新
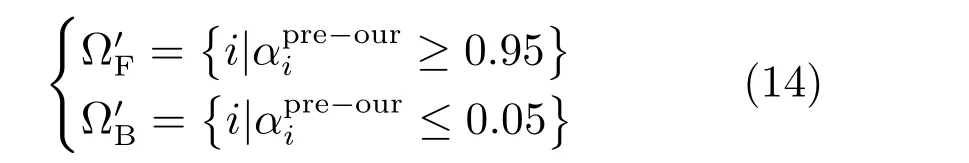
3 混合像素计算
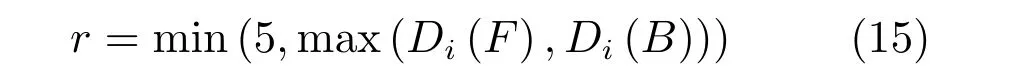
4 实验
4.1 绝对像素划分
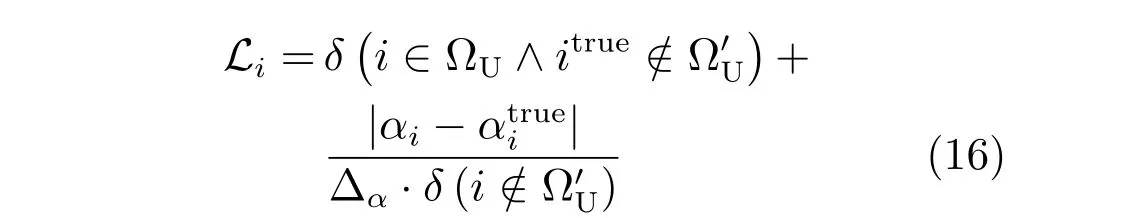

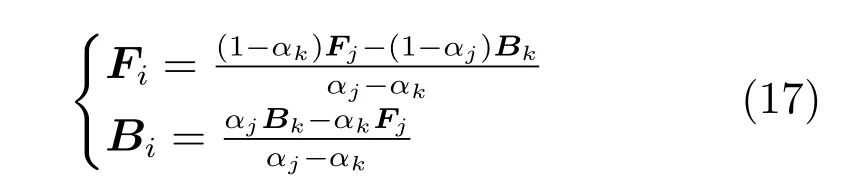
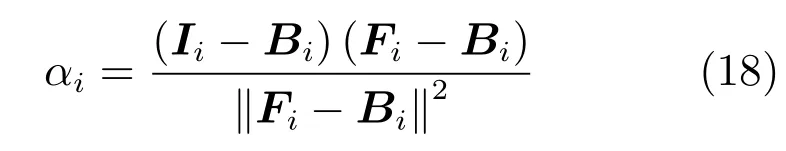
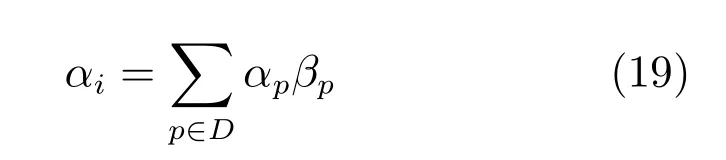
4.2 混合像素计算
4.3 算法的整体评价
5 讨论与后续工作
6 结论
