绝对值函数的一类新的光滑近似
2021-03-04王俊
王 俊
(江苏科技大学 理学院, 镇江 212100)
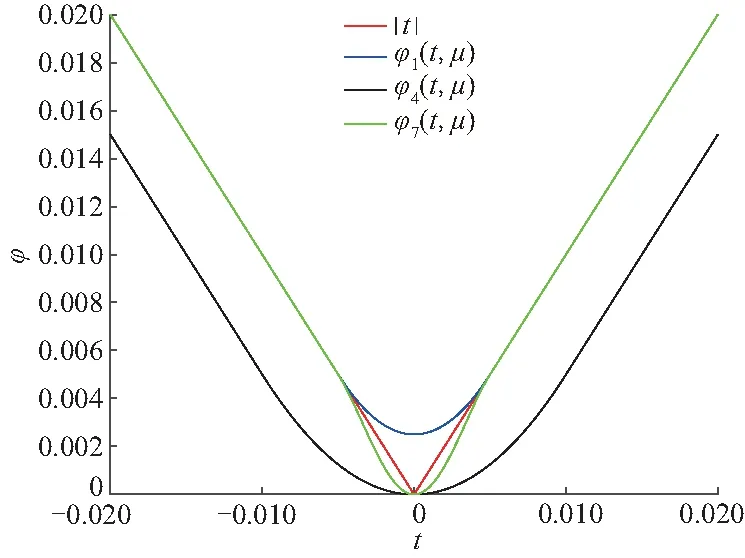
在最优化领域中,非光滑优化问题[1]越来越引起研究者的重视.主要是因为这些不可微的目标函数有一些实际的意义或者好的特性.比如,比较活跃的压缩感知领域中的lp(0 首先,给出连续不可微函数的光滑近似的定义,而连续可微函数又称为光滑函数. 另外,对于任意的t∈R,两类连续不可微函数绝对值函数|t|和最大值函数max{0,t}的等式关系: |t|=max{0,t}+max{0,-t} (1) 由式(1)说明这两类连续不可微函数是可以相互转化的.另外,需要特别指出的是,虽然最大值函数max{0,t}是连续不可微的,但是max2{0,t}是连续可微的,且其导函数为2max{0,t}. 文献[6,10,12-13]基于卷积的性质,利用分段连续的密度函数ρ:R→R+构造最大值函数的单参数光滑近似.需要注意的是,这个密度函数满足: (1) (对称性)ρ(s)=ρ(-s) (2) (有界性)有界常数 利用密度函数的两个性质,可以验证 是定义好的(well-defined).另外,对于任意给定的参数μ>0,φ(t,μ)关于变量t是连续可微的、凸的和严格递增的,而且还满足: 0≤|φ(t,μ)-max{0,t}|≤κμ 由不等式和定义1可得φ(t,μ)是max{0,t}的光滑近似,并且称这个常数κ为光滑近似的有界常数.显然,构造不同的密度函数可得不同的光滑近似函数. (i) 取 那么 称为max{0,t}的光滑近似.再由式(1)有: 是绝对值函数|t|的光滑近似. 称为max{0,t}的光滑神经网络近似.结合式(1)可得: 是绝对值函数|t|的光滑近似.又因为 max{x1,x2}=x1+max{0,x2-x1} 则 是max{x1,x2}的光滑近似.进一步把以上结果推广到n维欧式空间Rn上可得: 是max{x1,x2,…,xn}的一个光滑近似. 称为max{0,t}的CHKS[9]光滑近似.结合式(1)可得: 是绝对值函数|t|的一个光滑近似. 又因为最大值函数max{0,t}是凸的和全局Lipschitz连续的,所以任意光滑近似φ(t,μ)也是凸的和全局Lipschitz连续的.另外,对于任意固定的t∈R,φ(t,μ)关于μ是连续可微的、单调递增和凸的,且满足对于μ2>μ1>0, 有: 0≤φ(t,μ2)-φ(t,μ1)≤κ(μ2-μ1) 任意给定的连续函数g:dom(g)→R,其凸共轭g*:(dom(g))*→R定义: 式中,dom(g)为函数g的定义域.利用凸共轭的定义,可以构造g的光滑近似: 式中,d为1-强凸函数[14]. 是绝对值函数|t|的光滑近似,并被称为经典的Huber函数.于是由式(1)得: 是max{0,t}的光滑近似. 在如下的情况 有 (iv) 取d(z)=z1log(z1)+z2log(z2)+z2log(z2),可得: 是|t|的光滑近似.于是有: 是max{0,t}的光滑近似. 是|t|的光滑近似.另外,由式(1)可得: 是max{0,t}的光滑近似. 对于几类绝对值函数的光滑化近似函数,可以得到一个重要结果[7].需要指出的是,在不同的实际问题中,这个结论可以指导如何选取合适的光滑近似. 定理1[10]对于任意给定的参数μ>0和t∈R, 则: a)φ1(t,μ)≤φ2(t,μ)≤φ3(t,μ) b)φ6(t,μ)≤φ5(t,μ)≤φ4(t,μ) c)φ4(t,μ)≤|t|≤φ1(t,μ) 值得注意的是,由定理1可知,在φi(t,μ),i=1,2,…,6中,φ1(t,μ)和φ4(t,μ)是逼近绝对值函数的效果最好的上下界光滑近似,所以根据实际需要优先选择这两个近似函数.图 1说明,当取参数μ=0.01时,上界光滑近似函数φ1,φ2和φ3的局部性质.显然上界光滑近似中效果最好的是φ1, 这和定理1的结果是一致的. 图1 当参数μ=0.01, 光滑近似φ1和φ2与φ3的比较 图2表明,当参数μ=0.01时,下界光滑近似函数φ4,φ5和φ6的局部性质.显然,这些下界光滑近似中,逼近效果最好的是φ4,这也验证了定理1的结果. 图2 当参数μ=0.01, 光滑近似φ4和φ5与φ6的比较 现在考虑一类带有双参数α和μ的最大值函数max{0,t}的光滑近似[15]: 其中,0≤α≤1和μ>0.α控制光滑近似函数的逼近精确度和μ决定对于任意的t∈R,近似函数φ(t,α,μ)是否更加精确.当然,μ的解释也适用于其他几类近似函数.再利用式(1)可得: 是|t|的一个光滑近似.当α=1/2时,可由 得φ(t,1/2,μ)=φ4(t,μ).在一定程度上,可以把φ(t,α,μ)看作是φ4(t,μ)的一个推广.然而,有个问题:对于其他的参数α≠1/2, 这两个近似函数φ(t,α,μ)和φ4(t,μ)的大小关系. 定理2[1]对于任意的α∈[0,1],μ>0和∀t∈R,有如下的不等式成立: b) 0≤|t|-φ(t;α,μ)≤2μmax{α2,(1-α)2}; c) -2(1-2α)2μ≤φ(t;α,μ)≤2μα(1-α) 构造并证明一个关于绝对值函数的光滑近似函数,是文中的重要结果之一. 定理3对于任意的t∈R和参数μ>0,则 是绝对值函数|t|的光滑近似,且 0≤|t|-φ7(t,μ)≤κ7μ 其中 所以近似函数φ7(t,μ)关于t是连续的.其次, 故有 因此φ7(t,μ)是连续可微的.然后,利用φ7(t,μ)=φ7(-t,μ)和其定义域是对称的,可得: 于是有0≤|t|-ω(t,μ)≤κ7μ. 最后,再由定义1可证φ7(t,μ)是绝对值函数的一个光滑近似.因此,定理3得证. 利用定理3和式(1), 可得到: 是max{0,t}的光滑近似. 对比φ7(t,μ)与之前的光滑近似φi(t,μ),i=1,2,…,6.一个最直接、最有效和最简单的方法是比较有界常数κ的大小,几类光滑逼近函数的有界常数κ,见表1. 表1 绝对值函数的几类光滑近似的有界常数 一个判断标准是有界常数κ越小,逼近效果越好.实际上,利用光滑近似函数的有界常数κ也可以判断这七类近似函数的优劣.可以看到φ1和φ4是他们中除去φ7之外,逼近效果最好的上下界光滑近似,这与定理1中给出的结论是符合的.然而对于绝对值函数的下界光滑近似,从定理3以及表1中的有界常数κ7<κ4可得到光滑近似φ7比已知的φ4更好.进一步地,当μ=0.01, 图3更是验证了以上的分析结果,而且还表明光滑近似φ7比φ4和φ1的逼近更好. 图3 当参数μ=0.01, 光滑近似φ1和φ4与φ7的比较 (1) 基于正弦函数构造了一类新颖的光滑逼近函数,并通过引进有界常数来说明新构造的光滑近似的逼近效果有一个精度的提升. (2) 在实际工程应用中推荐选用光滑近似φ1,这是因为最小化φ1便是可以迫使绝对值函数也取得最小,即|t|≤φ1(t,μ).而且,已有的文献中,在图像处理、稀疏优化、回归分析、神经网络、复杂系统以及深度学习等领域中,只要涉及绝对值函数的光滑近似的,一般都是选择φ1. (3) 若是不需要作最小化处理,仅仅是为了在理论分析中使用,那么可选择逼近效果更好的光滑近似φ7.1 光滑近似函数

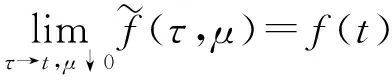

1.1 基于卷积的光滑近似
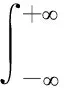

1.2 基于凸共轭的光滑近似
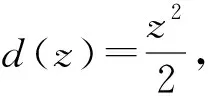


1.3 双参数的光滑近似
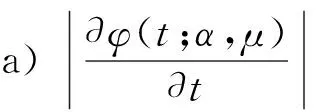
1.4 下界光滑近似
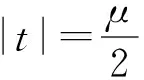



2 结论
