小回线瞬变电磁法多匝回线电感研究
2021-03-04连晨光石显新
连晨光,石显新
(1.煤炭科学研究总院,北京100013;2.中煤科工集团西安研究院有限公司,陕西 西安710077)
瞬变电磁法(简称TEM 法)观测纯二次场,对低阻体敏感,对野外场地的适应能力强, 施工效率高,是探测与煤矿水害隐患有关的异常地质体的重要手段,在煤田水文地质勘探中得到广泛应用。小回线瞬变电磁法对传统瞬变电磁法的探测装置进行了改进,采用边长几米(一般1~5 m)的多匝方形回线发射、同一回线接收或中心探头接收的方式进行探测。由于小回线装置受地形影响小、可在地面障碍物密集、施工场地狭小(如井下巷道)等地段进行有效探测,施工灵活方便,体积效应小,因此小回线瞬变电磁法在山地、隧道、煤矿井下及其他施工布置困难地区的含水地质异常体探测中得到广泛应用,并取得了较好的效果[1]。为增加探测深度、提高抗干扰能力,小回线瞬变电磁法除尽可能增大发射电流外,一般通过增加回线的匝数进而增大发射磁偶极矩来实现。因此线圈自感和互感影响较突出。而多匝回线之间的自感和互感影响往往会造成瞬变电磁法测量早期信号严重失真[2],导致计算的视电阻率普遍偏低,与实际情况严重不符。因此,准确计算出线圈的自感和互感,从而消除其影响对小回线瞬变电磁法探测具有重要意义。
关于回线电感的研究,国内外学者已经做了大量的研究。自感方面,Green House 将线圈看成同等长度的直导体,给出的回线自感互感表达式[3],计算方便;《电感计算手册》虽以简化公式、图表以及数据表的形式给出单匝矩形线圈自感表达式,但使用不便[4];蒋邦远、牛之琏给出了单匝矩形线圈自感计算公式[5,-6],误差极大;李文尧等推导出单匝矩形线圈自感精确解析式和近似式[7];薛国强等以近似公式计算出了单匝线圈自感[8-9];杨海燕等对多匝圆回线的自感互感计算公式进行了大量的研究,给出了多匝线圈电感的近似公式[10-12];武中华等推导出圆形回线自感积分表达式,并用matlab 进行了数值计算,虽精度较高,但计算较为复杂[13];罗垚、吴德会等采用有限元方法对矩形截面圆线圈自感进行研究,给出计算线圈自感的公式,提高了计算速度[14-16]。在回线互感方面,Christian Peters 等基于毕奥萨伐尔定律计算出回线的互感,只能直接计算出整个回线的互感[17-18];嵇艳菊、刘洋等则利用Neumann 公式计算出了回线的互感,可以计算回线部分电感,进行累加求出回线的总互感[19-22]。
但目前对多匝回线自感互感常用公式的准确性比较与适用性分析少有人研究,因此总结目前常用的的多匝回线自感互感计算公式,主要包括圆形回线自感计算、矩形回线自感计算、互感计算3 个方面,比较分析现有公式的自感互感值及其误差,以便选出准确的公式来计算小回线电感,为小回线瞬变电磁法电感影响的消除提供依据。
1 多匝回线自感计算公式
在瞬变电磁法中,回线的自感参数主要应用于局部导体晚期瞬变电磁场的等效计算、接收线圈固有过渡过程计算、关断时间计算及其瞬变电磁仪器研制方面[6]。
线圈自感的计算有数值解法和解析解法,解析解法又分为近似解析解和精确解析解2 种[7]。
1.1 矩形回线自感计算公式比较
利用蒋邦远、牛之琏、杨海燕、Green House、薛国强、李文尧等学者给出的矩形回线自感计算公式[2-3,5-7,9,11],在导线半径为0.001 m,线圈匝数为1,回线边长为1~5 m 的方形单匝线圈下,以李文尧给出的矩形回线自感解析公式作为理论值,计算其余公式自感值及其相对误差,方回线自感值及自感误差见表1。
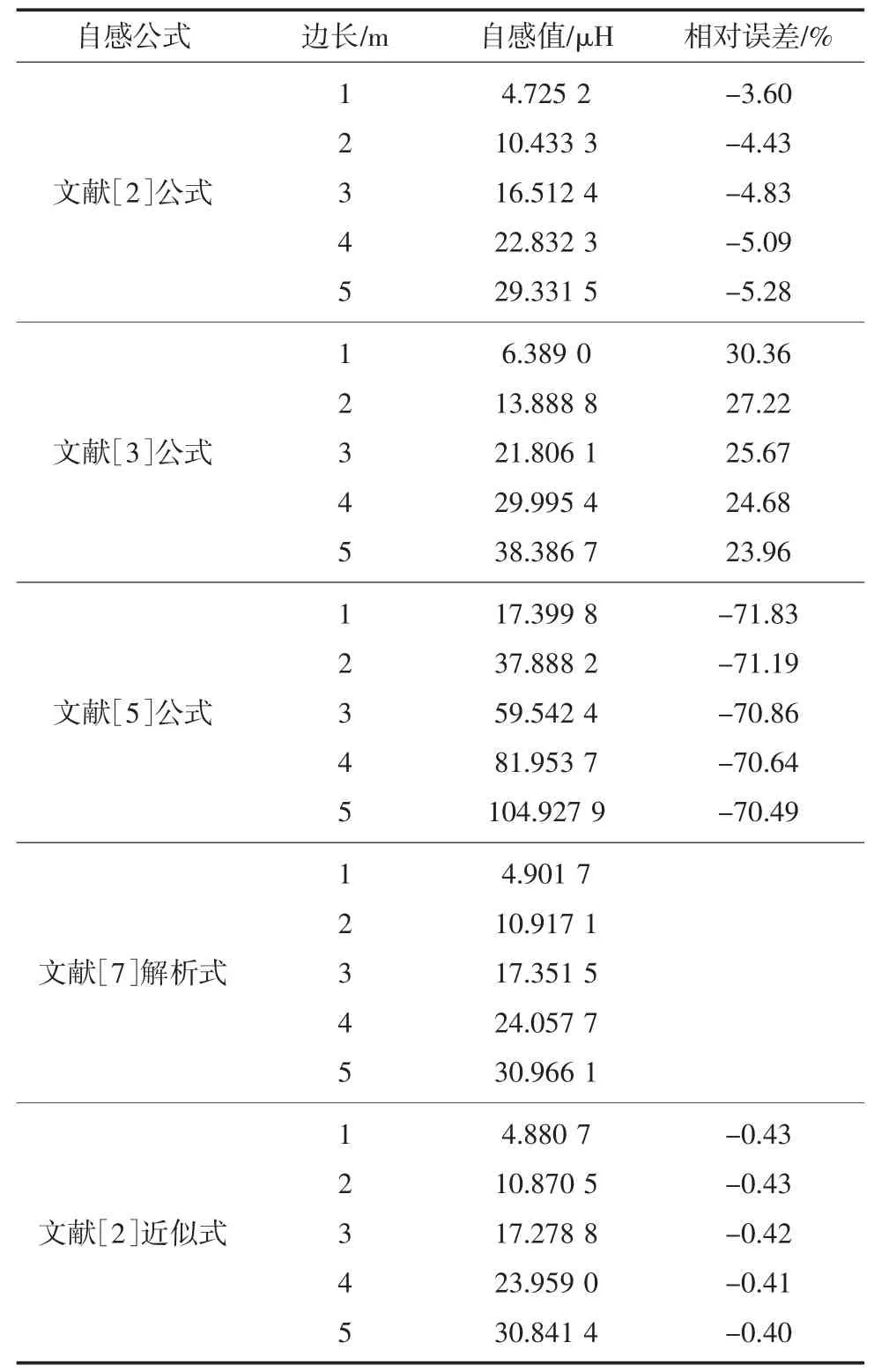
表1 方形回线自感值及自感误差Table 1 Error of self-inductance of square loop
通过matlab 计算发现,文献[6]和文献[9]中公式的计算结果与理论值相差多个数量级,因此不在表1 中出现,不建议使用。从表1 中可以看出,计算的方形回线自感值都会随着线圈边长的增大呈现线性增大的趋势。文献[5]中公式计算的自感值与理论值相差多个数量级,误差大。
从表1 中可以清晰地比较出各个公式与理论值的误差百分比,当方形线圈边长为1~5 m 范围内,文献[2]中公式相对误差为-3.60%~-5.28%,文献[3]中公式相对误差为30.36%~23.96%,文献[7]中近似式相对误差为-0.43%~-0.40%。
因此,可以得出计算方形线圈自感值可以采用文献[2]和文献[7]中给出的公式。
1.2 圆形回线自感计算公式比较
利用杨海燕、李文尧、Green House 等学者给出的圆形回线自感公式[3,7,11],在导线半径为0.001 m,线圈匝数为1,半径为1~5 m 的圆回线,利用杨海燕给出的圆回线自感公式自感值作为理论值,计算其余公式自感值及其相对误差。圆回线自感值及自感误差见表2。
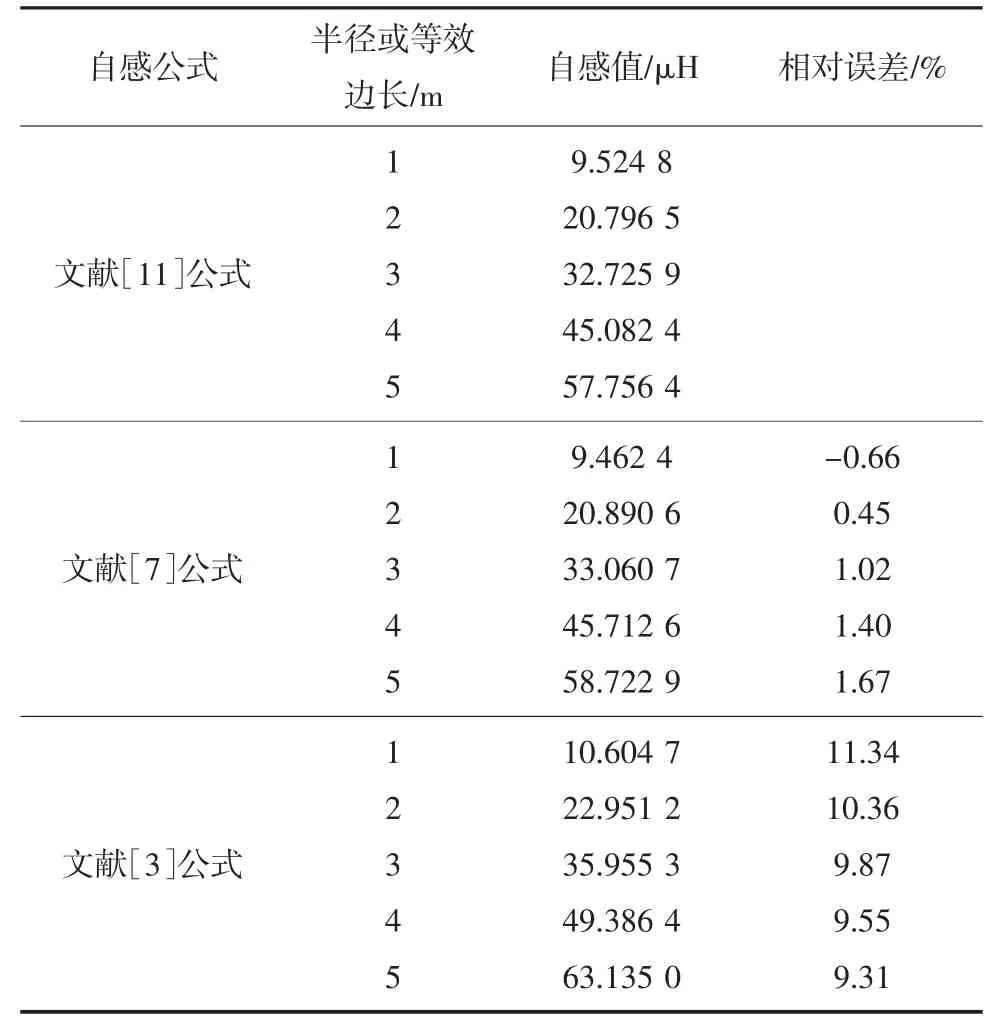
表2 圆回线自感值及自感误差Table 2 Error of self-inductance of circular loop
从表2 中可以看出,随着圆回线半径的增加,自感值也呈线性增加,与矩形回线类似。文献[11]和文献[7]中的公式计算出的圆回线自感值相差较小。在半径为1~5 m 的范围内,文献[7]中根据矩形自感公式利用圆回线和方回线等磁距求得的计算公式,误差为-0.6%~1.67%。文献[3]则是将圆回线看成长度相同的直导体,误差为在11.34%~9.31%,误差相对较大。
因此,可以得出文献[11]和文献[7]中的公式可以作为计算圆回线自感的计算公式。
2 小回线互感计算
任何2 个线圈之间都存在互感,互感系数有线圈的几何形状、尺寸、匝数及线圈之间的相对位置决定[23]。回路电感和部分电感是计算线圈之间互感的2 种主要方法[24]。回路电感即直接计算出整个回线的互感,主要利用毕奥萨伐尔定律进行计算,如杨海燕、Christian Peters、Yuhua Cheng 等给出的回线互感计算公式[11,17-18]。部分电感则是将发射回线和接收回线分为多个部分,利用Neumann 公式等分别就算出这些部分之间的互感,累加求出回路互感值,如嵇艳菊、刘洋、Hadi Tavakkoli、Salahuddin Raju 线圈互感的计算公式[19-22]。
研究矩形回线互感公式,为了方便计算,将其设置为方形回线,设置2 个平行的边长相等的方回线,回线边长为1~5 m,导线半径为0.001 m,匝数N=1,2 个回线距离z=0.001 m,比较各个公式计算出的互感值,同时以Yuhua Cheng 给出的公式计算的互感值作为理论值,计算其余公式的相对误差,方回线互感及互感误差见表3。
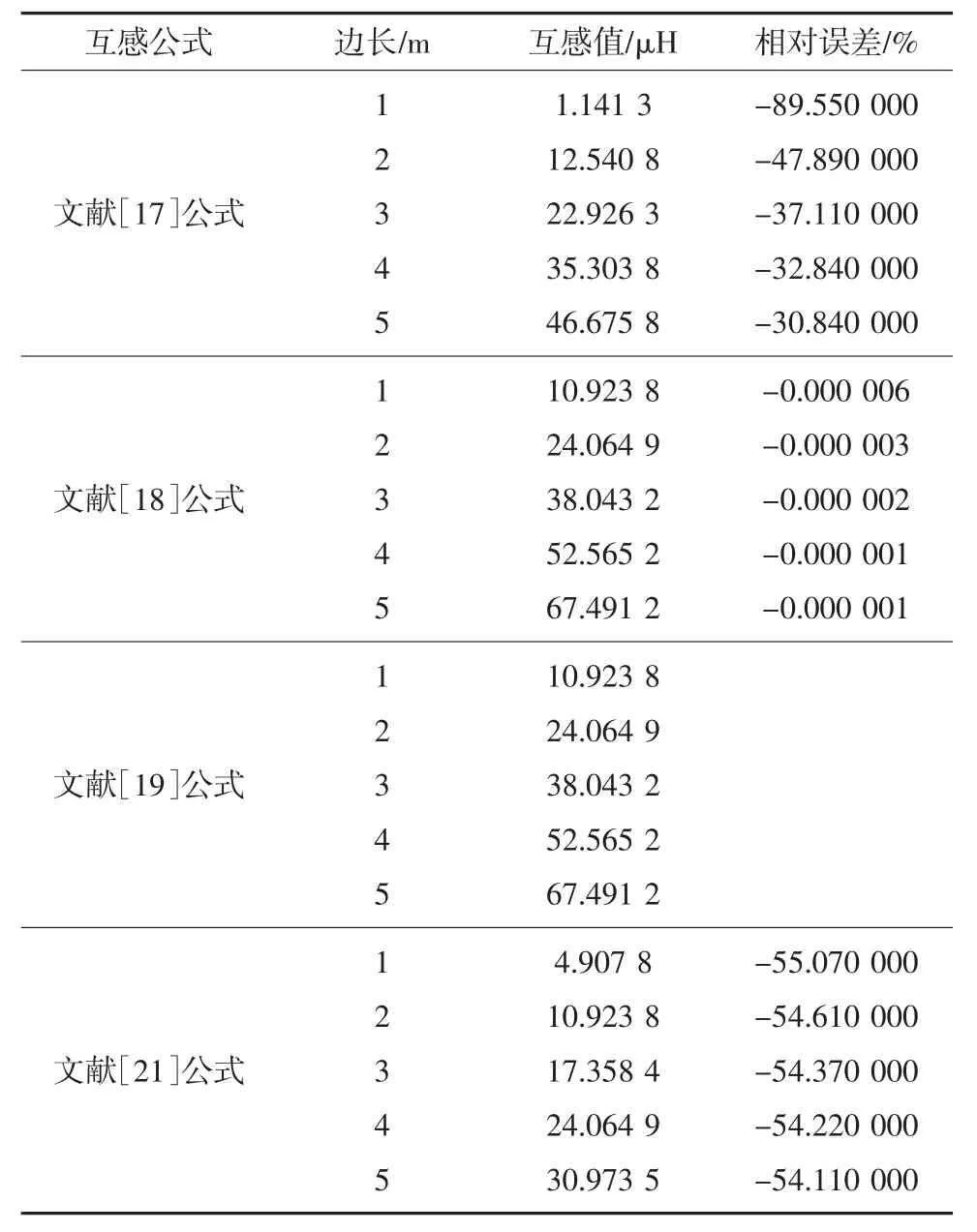
表3 方回线互感及互感误差Table 3 Error of mutual inductance of square loop
由表3 可知,随着方回线边长的增加,回线之间的互感值逐渐增加。文献[18]和文献[19]中给出的计算公式计算结果误差极小,几乎重合。而文献[17]和文献[21]中的公式计算的互感值差距较大,相差约1 个数量级。文献[17]中公式的相对误差在边长为1~5 m 的范围内,误差达到-89.550 000%~-30.840 000%,文献[21]中的公式的相对误差为-55.070 000%~-54.110 000%,误差极大,不适用,而文献[18]中公式的相对误差小于1%。
因此在计算平行方形回线互感时,可以采用文献[18]和文献[19]中的计算公式。
为研究圆回线互感公式,设置2 个平行的半径相同的回线,回线半径为1~5 m,导线半径0.001 m,匝数N=1,2 个回线距离z=0.001 m,比较各个公式计算出的互感值,以文献[11]中给出的解析公式计算的互感值作为理论值,计算与近似公式及其文献[22]公式的相对误差。圆回线互感及互感误差见表4。
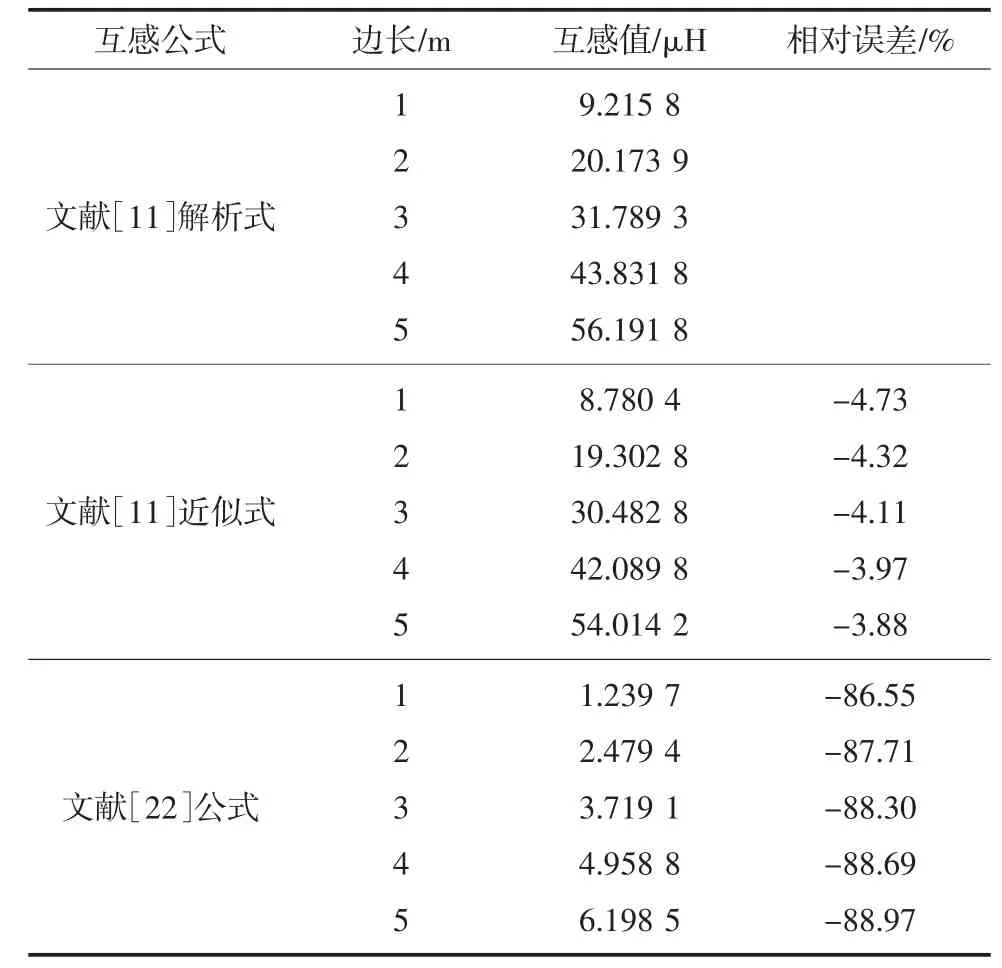
表4 圆回线互感及互感误差Table 4 Error of mutual inductance of circular loop
从表4 中可以看出,当两平行圆回线之间距离时,文献[11]近似公式与解析式计算出的结果相差很小,但文献[22]对椭圆积分进行级数展开时所得的近似公式存在较大误差。从表4 中得到,在半径为1~5 m 时,文献[11]中近似公式误差在-3.88%~-4.73%,文献[22]中近似公式误差达到-86.55%~-88.97%,误差极大,不适用,因此在计算圆形线圈互感时可以选用文献[11]中的公式。
回线总电感为所有回线的自感与回线之间互感的和[25]:

式中:LT为回线总电感;n 为线圈匝数;Li为线圈自感;Mij为回线互感。
3 结 语
在考虑实际多匝回线大小(边长或半径为1~5 m)的前提下,计算了圆回线和方回线不同计算公式所计算出的自感式互感值,并分析其相对误差,发现当边长为1~5 m 的方回线,利用文献[2]和文献[7]中的公式来计算其自感误差小于5%,文献[18]和文献[19]计算其互感较准确。当半径为1~5 m 时的圆回线,利用文献[7]和文献[11]公式计算自感,其误差小于5%,利用文献[11]中的计算公式计算互感较准确。
在矿井瞬变电磁中,计算多匝回线的自感互感,往往忽略了导线的宽度、厚度、截面形状、缠绕方式等影响,在做精细测量中,应该给予考虑。同时,在实际生产活动中,不仅要准确计算出多匝回线的互感自感,也要分析回线电感随时间的变化规律,而目前根据RCL 等效电路分析给出的自感电流电压的时间域方程,未考虑到地质体典型特征的影响,应进行理论研究和分析。
