基于自适应卡尔曼滤波的梯次电池荷电状态估算
2021-03-04柴建勇侯恩广李岳炀
柴建勇,侯恩广,李岳炀
(1. 山东高速信息集团有限公司,山东济南250101; 2. 山东交通学院轨道交通学院,山东济南250357;3. 济南大学自动化与电气工程学院,山东济南250022)
我国近几年的动力电池产销量已经位居全球前列,这些动力电池在未来几年中将逐步退役,因此研究退役动力电池的梯次利用,对间接降低动力电池成本和解决环境污染问题具有重要的意义[1-3]。
梯次电池处于离线状态,并且单体电池一致性很差,因此需对其性能进行重新测试和评价。国内梯次电池的研究主要集中在退役电池储能应用和基站应用等层面,少数研究涉及了梯次电池的性能测试和评价方法,主要从锂电池电压、内阻、容量、温升等外特性的测试入手,较少提及其全生命周期的电池模型及荷电状态(SOC)的估算[4-11]。
本文中基于自适应卡尔曼滤波算法,提出梯次电池SOC的估算方法。在通用的卡尔曼滤波算法的基础上,引入自适应估计原理,实时估算时变噪声,提高滤波的稳定性,增强自适应特性。
1 梯次电池全生命周期等效模型
本文中采用二阶Thevenin模型作为梯次电池的全生命周期模型,等效电路如图1所示。
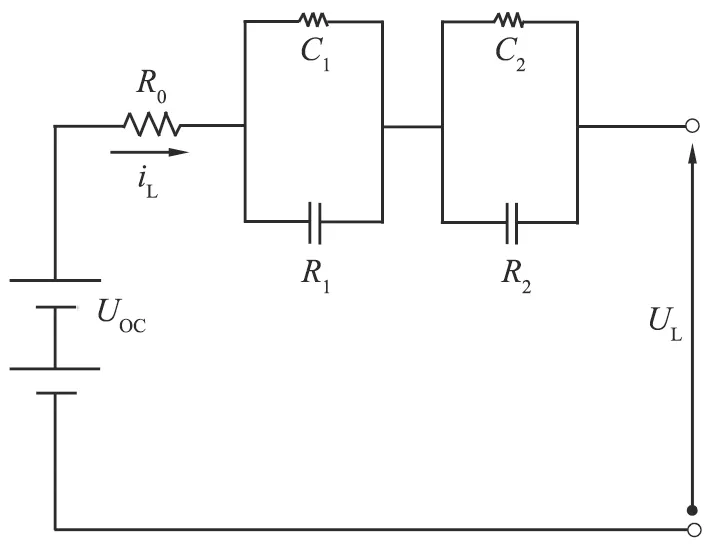
UL—梯次电池工作电压; R1、R2—梯次电池的极化内阻; UOC—梯次电池的开路电压; R0—梯次电池的欧姆内阻; C1、C2—等效电容; iL—充放电电流。图1 二阶Thevenin模型等效电路图
由图可以看出,梯次电池全寿命周期模型等效电路的数学表达式为
(1)
(2)
UL=UOC-U1-U2-iLR0,
(3)

梯次电池的全寿命周期模型等效电路的离散状态方程、离散观测方程分别为
(4)
ikR0+ϑk,
(5)
令
得
f(xk,uk)=Akxk+Bkuk,
(6)
g(xk,uk)=Ckxk-R0uk,
(7)
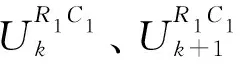
2 动模型参数辨识
本文中主要研究3种梯次电池参数的辨识,分别是梯次电池的开路电压、欧姆内阻和极化内阻。
2.1 梯次电池开路电压
开路电压UOC的获取步骤如下:
1)把梯次电池充满电,即充电到单体电压为4.25 V停止;
2)以0.5C(充放电速率,2 h完成充放电的电流为0.5C)的电流放电,放电到单体电压2.8 V停止,记录放电电压Ud;
3)以0.5C的电流充电,充电到单体电压为4.25 V停止,记录充电电压Uc;

图2 梯次电池开路电压曲线
2.2 欧姆内阻的计算
2.3 极化内阻的辨识
通过充放电实验测试得到的梯次电池工作电压UL、充放电电流iL和开路电压UOC。应用最小二乘法,使残差的平方和最小,辨识参数模型。此方法在文献[13]中有详细介绍,因此不再赘述。
3 基于自适应卡尔曼滤波的估算方法
传统的卡尔曼滤波算法在实施过程中假定过程噪声和测量噪声均值为0,但是在实际应用中噪声均值为0的情况并不存在,噪声统计特性经常引起滤波发散。为了解决这一问题,本文中引入自适应滤波技术,采用基于自适应卡尔曼滤波的估算方法来抑制噪声,提高SOC估算精度[14-17]。
系统离散状态空间模型如下。
状态方程为
xk+1=f(xk,uk)+ωk,
(8)
输出方程为
yk=g(xk,uk)+ϑk。
(9)
结合传统的卡尔曼滤波算法,得出如下基于自适应的卡尔曼滤波算法方程。
状态变量估计方程为
(10)
观测变量估计方程为式(9),误差协方差预测方程为
(11)
卡尔曼增益方程为
(12)
状态变量最优估算方程为
(13)
误差协方差最优估算方程为
(14)
过程噪声协方差方程为
(15)
观测噪声协方差方程为
(16)
4 仿真分析
为了验证该算法的自适应特性、准确性和收敛性,对充满电状态的梯次电池进行放电实验,从SOC为100%时开始,放电截至到SOC为25%。在实验过程中,把SOC初始值分别改变到30%、50%、60%,观察分析SOC自适应曲线、SOC误差曲线、观测噪声协方差R变化曲线和过程噪声协方差Q变化曲线。
SOC初始值不同时的SOC自适应曲线如图3所示。由图可以看出,对于SOC初始值分别为30%、50%、60%的情况,本文中提出的算法都可以进行自适应调整,具有自适应特性。
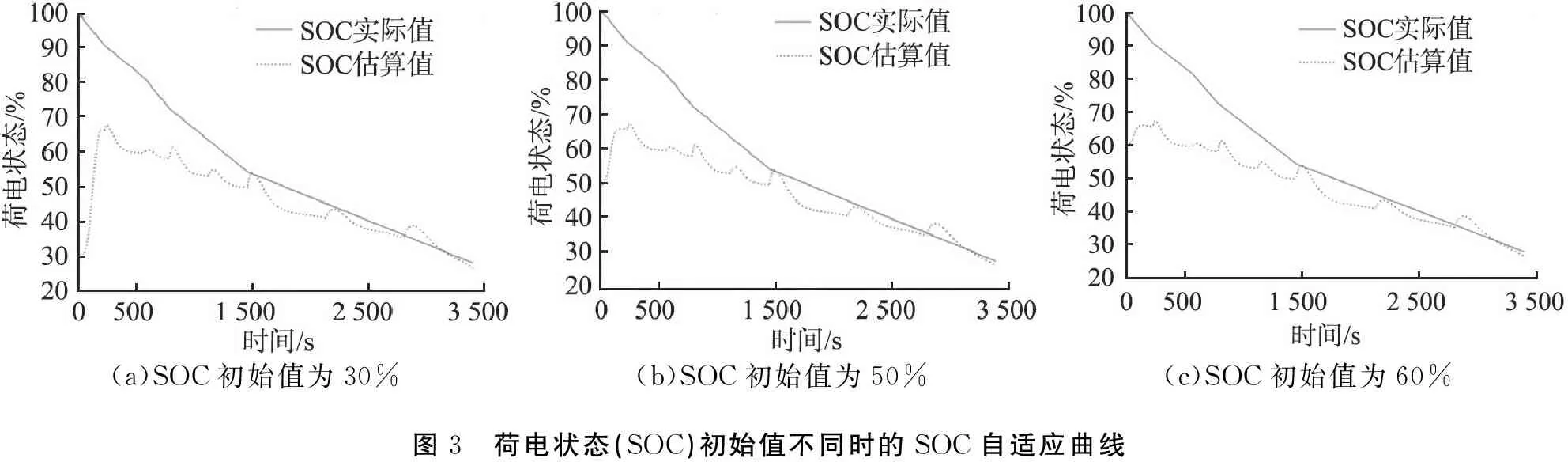
(a)SOC初始值为30%(b)SOC初始值为50%(c)SOC初始值为60%图3 荷电状态(SOC)初始值不同时的SOC自适应曲线
SOC初始值不同时的SOC误差曲线如图4所示。由图可以看出,对于SOC初始值分别为30%、50%、60%的情况,SOC调整后估算误差小于3%,具有较高的准确性。
SOC初始值不同时观测噪声协方差R的变化曲线如图5所示。由图可以看出,对于SOC初始值为30%、50%、60%的情况,观测噪声协方差R一致收敛,具有收敛性。

(a)SOC初始值为30%(b)SOC初始值为50%(c)SOC初始值为60%图4 荷电状态(SOC)初始值不同时的SOC误差曲线
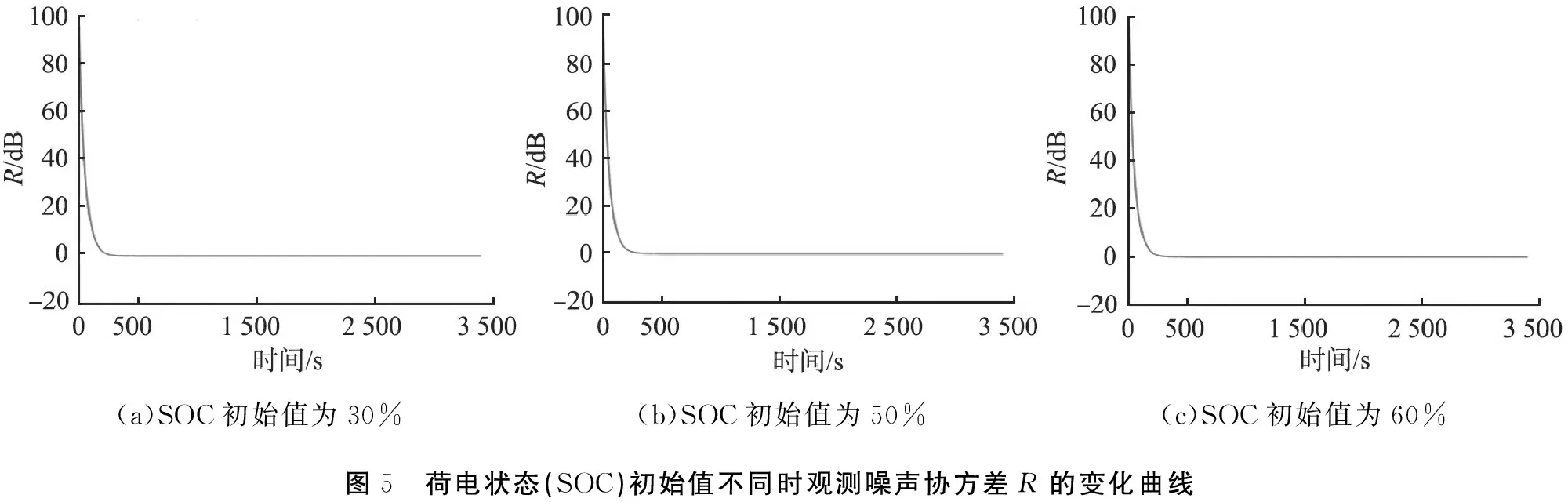
(a)SOC初始值为30%(b)SOC初始值为50%(c)SOC初始值为60%图5 荷电状态(SOC)初始值不同时观测噪声协方差R的变化曲线
SOC初始值不同时观测噪声协方差Q的变化曲线如图6所示。由图可以看出,对于SOC初始值为30%、50%、60%的情况,过程噪声协方差Q在每次电流变化后都可以进行调整,并且具有收敛性。

(a)SOC初始值为30%(b)SOC初始值为50%(c)SOC初始值为60%图6 荷电状态(SOC)初始值不同时过程噪声协方差Q的变化曲线
5 结论
通过仿真验证可知,在SOC初始值不明确的情况下,本文中提出的基于自适应卡尔曼滤波算法的梯次利用电池SOC估算方法,具有自适应特性和收敛性,能够快速调整到正确的轨迹,并且SOC估算误差小于3%,具有较高的准确性。本方法对于梯次电池的推广应用具有参考价值。
