RR-P5R型全球面工作空间解耦并联机构误差分析
2021-03-04于珊珊李为民杨先海
于珊珊,李为民,杨先海
(1. 河北工业大学机械工程学院,天津300130; 2. 山东理工大学机械工程学院,山东淄博255000)
球面并联机构是一种具有重要应用价值的并联机构[1-3]。与传统的串联机构相比较,球面并联机构的结构通常比较复杂,工作空间相对较小,且存在诸多不易计算的奇异位姿,对此,国内外学者展开了一系列的研究[4-6]。Tao等[7]开发了一种系统设计方法——最小干涉法(LIDeM),可以减少机构链接之间的干涉,增大机构的工作空间。李寒冰等[8]设计了一种新型2PUS-2PRU并联机构,可用于太阳追踪装置,并采用遗传算法对工作空间和灵巧度进行综合优化,优化后的工作空间在各方向上均明显增大。赵瑞杰等[9]提出一种新型3-PPR球面并联机构,得出了机构产生奇异位形的条件和奇异位形的类型,验证了3-PPR机构不存在奇异位置,机构的工作空间无空洞,是完整的少半球面。王超群等[10]针对三自由度3-RRR球面并联机构,基于四元数建立运动学模型,找到了机构碰撞干涉的条件,依据该条件对3-RRR机构进行优化设计,实现了完整的球面工作空间。
当前球面并联机构工作空间的研究主要集中在对现有机构的优化分析,但针对球面解耦并联机构工作空间最大化的研究仍比较少。面对当前科技发展对机构大工作空间的要求,如空间360°测量、空间定位定向、未知环境探测等,现有的球面解耦并联机构已无法满足大角域工作范围的需求,因此对全球面工作空间并联机构的研究显得尤为重要。
针对现有二自由度球面解耦并联机构工作空间不足的问题,本文中提出一种新型二自由度RR-P5R型球面解耦并联机构,以实现完整的球面工作空间,对该机构进行误差分析,为RR-P5R型机构的参数设计、控制以及误差补偿提供参考数据。
1 新型运动支链
图1所示为RR-PRR型球面解耦并联机构[11],动平台通过转动支链和直线输入支链与静平台相连。转动支链由转动副R1、R2组成,转动副R1的轴线为Y轴,转动副R2的轴线为X轴,轴线Y轴与X轴是正交的;直线输入支链由移动副P和转动副R3、R4组成。只有当直线输入支链中移动副P的输入方向平行于转动支链中转动副R1的轴线时才能实现机构的运动解耦。
RR-PRR型球面解耦并联机构转动支链输出角θ1的范围为[0°,360°]; 但是,由于摩擦圆的原因,直线输入支链控制的输出角θ2的范围区间总是包含于[0°,180°],通过运动耦合后,机构的工作空间并不是完整的球面,因此,如何使直线输入支链控制的输出角θ2的范围区间包含[0°,180°],成为全球面工作空间解耦并联机构构型研究需要解决的关键技术问题。
双摇杆机构的输入与输出具有以下特点:如果主动摇杆为最长杆件,则从动杆件的极限摆角大于主动摇杆的;如果从动摇杆为最长杆件,则主动杆件的极限摆角大于从动摇杆的。
结合双摇杆机构输入与输出之间存在差异化的特性,找到了使直线输入支链控制的输出角能够达到180°的解决方法。以双摇杆机构的长杆作为直线输入支链的输入,双摇杆机构的短杆作为直线输入支链的输出,使输出角极限大于180°,而输入角极限小于180°。根据二自由度球面解耦并联机构直线输入支链的构型要求,输入形式必须为直线输入,输出形式必须为转动输出,因此,可将双摇杆机构进行变型,得到P5R型运动支链,如图2所示。

R1、R2、R3、R4、R5、R6、R7—转动副; P—移动副; e—偏置距离; Y、Z—坐标轴。图2 P5R型运动支链
2 RR-P5R全球面解耦并联机构
基于P5R型直线输入支链,所设计的二自由度RR-P5R型全球面工作空间解耦并联机构的三维模型如图3所示。动平台通过转动支链和直线输入支链与静平台相连,即:转动支链由转动副R1和转动副R2组成,其旋转轴线相互正交,根据组成该支链称为RR运动支链;直线输入支链由移动副P和转动副R3、R4、R5、R6、R7组成,根据组成该支链称为P5R型运动支链。两者组成了RR-P5R型全球面工作空间解耦并联机构。
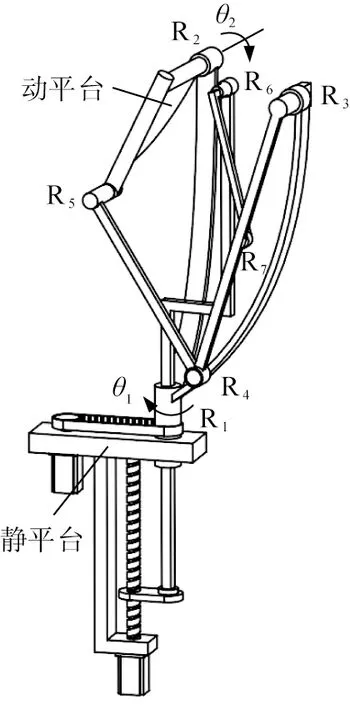
R1、R2、R3、R4、R5、R6、R7—转动副; θ1、θ2—输出量。图3 RR-P5R型全球面解耦并联机构
转动副R1由转动电机驱动,移动副P由直线电机驱动。移动副P的移动轴线与转动副R1的旋转轴线重合,且移动副P通过结构设计可以实现与转动副R1一同转动,而直线电机不会与转动副R1一同转动,可以有效减小转动电机的载荷。该机构的转动支链的输出角θ1的范围为[0°,360°],由直线输入支链控制的输出角θ2的范围为[0°,180°]。RR-P5R型球面解耦并联机构能够实现完整的球面工作空间。
3 机构相邻杆件间的变换矩阵
应用Denavit-Hartenberg(D-H)方法建立各构件的坐标系,如图4所示。转动副R1R2、R6R7、R3R4、R4R5之间的杆件依次标记为Link1、Link3、Link4、Link5。Link2为特殊形状杆件,其余均为直连杆。Link1的长度为L6,高度为L0,Link2的偏置距离为e,Link3的长度为L5,Link4的长度为L3,Link5的长度为L2,动平台的长度为L1,移动副P的位移量为P,θi(i=1,3,4,5,6,7,8)为绕Zi轴的相对转角。
设定坐标系XYZ固定于静平台,原点位于静平台与转动副R1的交点处; 坐标系XiYiZi(i=1,2,…,9)位于连杆上,各坐标系原点位于相应转动副的轴心,杆长方向设定为X轴,转动副轴线方向设定为Z轴,则根据右手螺旋准则可确定Y轴方向。

XiYiZi(i=1,2,…,9)—位于各转动副的坐标系; θi(i=1,3,4,5,6,7,8)—绕Zi轴的相对转角; Linki(i=1,2,…,5)—杆件。图4 RR-P5R型机构坐标系
设空间中任意一点在X1Y1Z1中的坐标为U1=(x1,y1,z1)T,在XYZ中的坐标为U=[x,y,z]T,则
(1)

(2)
(3)
(4)
(5)
(6)
(7)
(8)

Trans(0,-L0,0)Rot(z,θ8) ;
(9)

(10)
4 位姿误差分析
机构精度是机构性能的重要指标。实际机构从动件的位置、速度、加速度与理想机构从动件对应运动参数之间的误差,被称为机械误差[12-14]。虽然误差不可避免,但可以无限缩小,误差越小,机构的精度也就越高。研究机构精度,实际上就是研究机械误差。
4.1 位姿误差模型
结合上述杆件变化矩阵,采用环路增量法建立机构位姿误差模型。为了简化方程,c代表cos,s代表sin,c1表示cosθ1,s1表示sinθ1,以此类推。

(11)
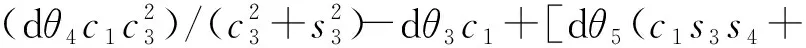
(12)
δZ=dθ1+{dθ6c1[c5(c3c4s1+s1s3s4)-s5(c3s1s4-
(13)
dX=dL3(c1c3s4-c1c4s3)+dL2[c5(c1c3s4-c1c4s3)+
s5(c1s3s4+c1c3c4)]+dec1+L6dθ3c1+Pdθ3c1+c1c3
[(dL3s4)/2-L5dθ4+L3dθ4c4]-L3dθ5(c1s3s4+
c1c3c4)-c1s3[dL5-(dL3c4)/2+L3dθ4s4]-dL2dθ6·
[c5(c1s3s4+c1c3c4)-s5(c1c3s4-c1c4s3)]-
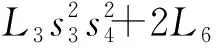
(14)
dY=dL3(c3s1s4-c4s1s3)+dL2[c5(c3s1s4-c4s1s3)+
s5(c3c4s1+s1s3s4)]+des1-L2dθ6[c5(c3c4s1+
s1s3s4)-s5(c3s1s4-c4s1s3)]+L6dθ3s1+dθ3Ps1+
c3s1[(dL3s4)/2-L5dθ4+L3dθ4c4]-L3dθ5(c3c4s1+
s1s3s4)-s1s3[dL5-(dL3c4)/2+L3dθ4s4]-
(15)
dZ=dL6+dP+dL2[c5(c3c4+s3s4)-s5(c3s4-c4s3)]-
dθ3e+dL3(c3c4+s3s4)+s3[(dL3s4)/2-L5dθ4+
L3dθ4c4]+c3[dL5-(dL3c4)/2+L3dθ4s4]+
L2dθ6[c5(c3s4-c4s3)+s5(c3c4+s3s4)]+
L3dθ5(c3s4-c4s3)+[dθ4c3(ec3+L6s3+Ps3)]/
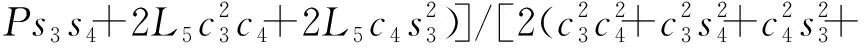
(16)
式中δX、δY、δZ、dX、dY、dZ即为RR&P5R型全球面工作空间解耦并联机构的位姿误差模型。
4.2 速度误差模型

RR-P5R型全球面工作空间解耦并联机构杆件之间的变化矩阵Ai对时间t求导后为
(17)
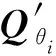
(18)
令
(19)
式(18)可化简为
(20)
已知
dAi=i-1ΔiAi,
(21)
式中i-1Δi为Linki在坐标系Xi-1、Yi-1、Zi-1中的误差,则
(22)
同理,有
(23)
式中:Ti=A1,A2,…,Ai,i=1,2,…,6;Δ为位姿误差。
因此
(24)
所以
(25)
化简得
(26)
应用
(27)
4.3 加速度误差模型
机构运动过程中末端产生的实际加速度与理想加速度之间的误差,即为加速度误差。
基于微分方程
(28)
(29)

(30)
(31)

(32)
(33)
以及
(34)
对式(22)求导,得
(35)
再对式(23)求导,得
(36)
则
(37)
5 结语
1)本文中针对现有二自由度球面解耦并联机构在大角域球面工作空间需求中存在工作空间不足的问题,基于双摇杆机构输入输出差异化特性,提出了一种新型P5R运动支链,该支链可用于构建二自由度全球面工作空间解耦并联机构。
2)基于新型P5R运动支链,设计了一种二自由度RR-P5R型全球面工作空间解耦并联机构。采用环路增量法对RR-P5R型球面解耦并联机构进行了误差分析,建立了机构相邻杆件间的变换矩阵,建立了机构的位置、速度、加速度误差模型。RR-P5R型机构的误差分析为机构的参数设计、控制以及误差补偿提供了理论基础。
