基于融合差异图的变化检测方法及其在洪灾中的应用

黄平平 段盈宏 谭维贤 徐 伟

(内蒙古工业大学信息工程学院 呼和浩特 010051)

(内蒙古自治区雷达技术与应用重点实验室 呼和浩特 010051)

1 引言

由于恶劣的气候和天气影响自然灾害频发，其中，洪灾严重破坏了生态环境，损害了私人和公共财产，对人类社会的生存发展有重大影响[1]。因此，对洪害前后进行变化检测，确定洪灾的淹没范围，对灾情的评估和灾后的管理规划都有一定的指导作用。合成孔径雷达(Synthetic Aperture Radar,SAR)可以全天时、全天候地获取遥感数据，不受光照和天气的影响，弥补了光学和红外遥感的不足。随着遥感技术的发展，不同时相、不同频带以及不同极化方式的多种SAR图像资源为SAR图像变化检测提供了数据基础，并广泛应用在灾区定位和灾害评估等方面[2]。

SAR图像的变化检测方法一般可分为两种[3]：监督和非监督。监督类变化检测方法需要大量的先验知识，而实际中往往缺乏真实的参考信息，适用范围较窄。非监督类变化检测方法不需要先验信息，可以直接对获得的两时相图像进行变化检测，在实际应用中更为广泛，且非监督类变化检测技术多在差异图生成和变化信息提取两方面进行创新。传统方法多使用不同的变化检测算子构建差异图，如经典的差值法和比值法[4,5]。相对熵，又被称为KL散度(Kullback-Leibler divergence)或信息散度，是两个概率分布间差异的非对称性度量，以此构造的差异图可衡量两幅影像间的相似程度。考虑到散斑噪声影响以及检测结果的精度，Gong等人[6]利用邻域像元灰度值和中心像元灰度值的相关性，提出一种基于邻域比值算子的差异图生成方法。单一类型的差异图像有自身的局限性，如均值比差异图对目标区域的群分性较好，但对纹理信息感知较弱，且存有大量噪声，对数比差异图在一定程度上削弱了背景部分的斑点噪声，但残留的噪声仍对后续处理有很大的影响[7–9]。基于此，一些研究人员选择使用图像融合的方法，利用不同差异图像的互补信息以及不同传感器的并行信息，在城市化和河口区域建筑的变化检测中展现了较好的结果[10–12]。在不同雷达图像数据中，通过融合多时相雷达数据以及相干和非相干性分析，对气旋、滑坡等灾害区域的评估也有一定的效果[13–15]。小波变换相对于轮廓波等多尺度变换而言，具有更小的计算复杂度，同时，小波变换可以将图像的时空信息转换为频域信息，进而可以方便地提取图像的详细信息，在图像融合中有广泛的应用[16–18]。在变化信息提取方面，Sumaiya等人[19]使用加权阈值分割对数均值比差异图，获得变化检测结果，计算过程快速简便。Zhang等人[20]利用广义高斯分布对差异图像的每一类进行建模，采用图割算法提取空间先验信息并通过模糊C均值算法很好地初始化模型的参数，在最大后验的贝叶斯准则下提取变化信息，其精度与算法速度都有一定的提升。Li等人[21]提出了一种称为SDPCANet的监督学习网络模型，该模型将显著性检测与主成分分析网络相结合，并在多时相SAR图像中验证了方法的有效性。Li等人[22]提出了一种基于卷积神经网络(Convolutional Neural Networks,CNN)的SAR图像变化检测新方法，该方法通过CNN直接从原始的两个SAR图像中生成分类结果，无需进行任何预处理操作，消除了生成差异图像的过程，从而减少了差异图对源图像的影响，并且在异质图像的变化检测中也有较好的效果。

洪灾发生时往往伴随着多云多雨，而光学传感器无法穿透云层，无法获取有效的地面信息，因此，SAR图像的变化检测更有效地应用在洪灾区域中。由于洪灾发生时降雨影响了地物散射特性[23]，在整幅图像中许多没有受洪灾影响的区域也呈现为伪暗区。在传统的差异图中，伪暗区与背景信息差异较大，而与变化信息更为接近，一般的变化检测算法更容易将伪暗区作为变化信息处理，这也导致了检测结果中较高的虚警率和较低的检测精度[24]。由于伪暗区的存在，对差异图的直接聚类易导致较多的错误信息，故可利用皮尔逊相关系数对模糊局部信息C均值(Fuzzy Local Information C-Means,FLICM)聚类方法的初始聚类结果进行二次分类，减小对检测结果的影响。一般而言，洪水淹没区域的相关系数更低，而标准未变化区域的相关系数更高，所以通过比较待定区域的相关系数，待定区域的类别，更容易划分为变化区域和未变化区域中两者相关系数均值更小的类别[25–28]。

本文结构安排如下：本文第2部分提出了一种利用融合差异图的SAR图像变化检测方法，然后在此差异图下得到基于相关系数FLICM算法二次分类后的检测结果，最后经迭代条件模型和马尔科夫随机场(Iterative Conditional Model-Markov Random Field,ICM-MRF)算法优化得到变化检测最终结果；第3部分首先利用Bern地区的ERS-2实测SAR数据以及加拿大Ottawa地区的Radarsat实测SAR数据进行结果分析并验证本文方法的有效性，之后利用该方法对中国鄱阳湖区域2020年6月和7月洪灾前后的Sentinel-1-A实测SAR数据进行分析，进而对受灾面积和其后的灾害趋势进行评估；第4部分对全文做出总结。

2 SAR图像变化检测算法

本文算法流程主要由融合差异图构造和ICMMRF分割[29,30]两部分组成，算法流程如图1所示。

融合差异图构造：首先得到两幅SAR图像的均值比差异图和利用邻域异质性信息的相对熵差异图，然后经小波变换，通过加权平均的方式将两幅图像的低频系数重构，与各自的高频系数，经小波逆变换得到两幅融合低频系数后的差异图，通过局部能量法融合为最终的差异图。

ICM-MRF分割：在ICM-MRF算法中，使用FLICM算法将变化检测结果分为3类，分别为变化区域、未变化区域和待定区域，对待定区域通过洪灾前后图像的皮尔逊相关系数(后简称为相关系数)进一步分为变化区域和未变化区域，并以此作为初始分割，得到最终的变化检测结果。

2.1 融合差异图构造

假设X1,X2为已经过配准预处理的两时像SAR洪灾前后变化区域图像，则离散图像数据X2对X1的相对熵可表示为

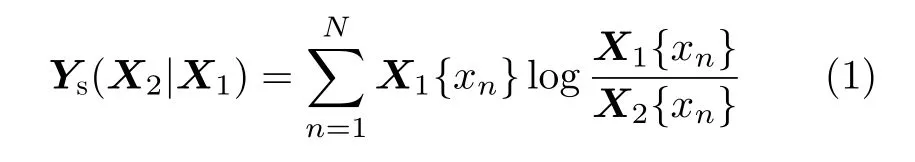
其中，N表示像元总个数，xn表示第n个像元的值，Ys表示X2对X1的相对熵。

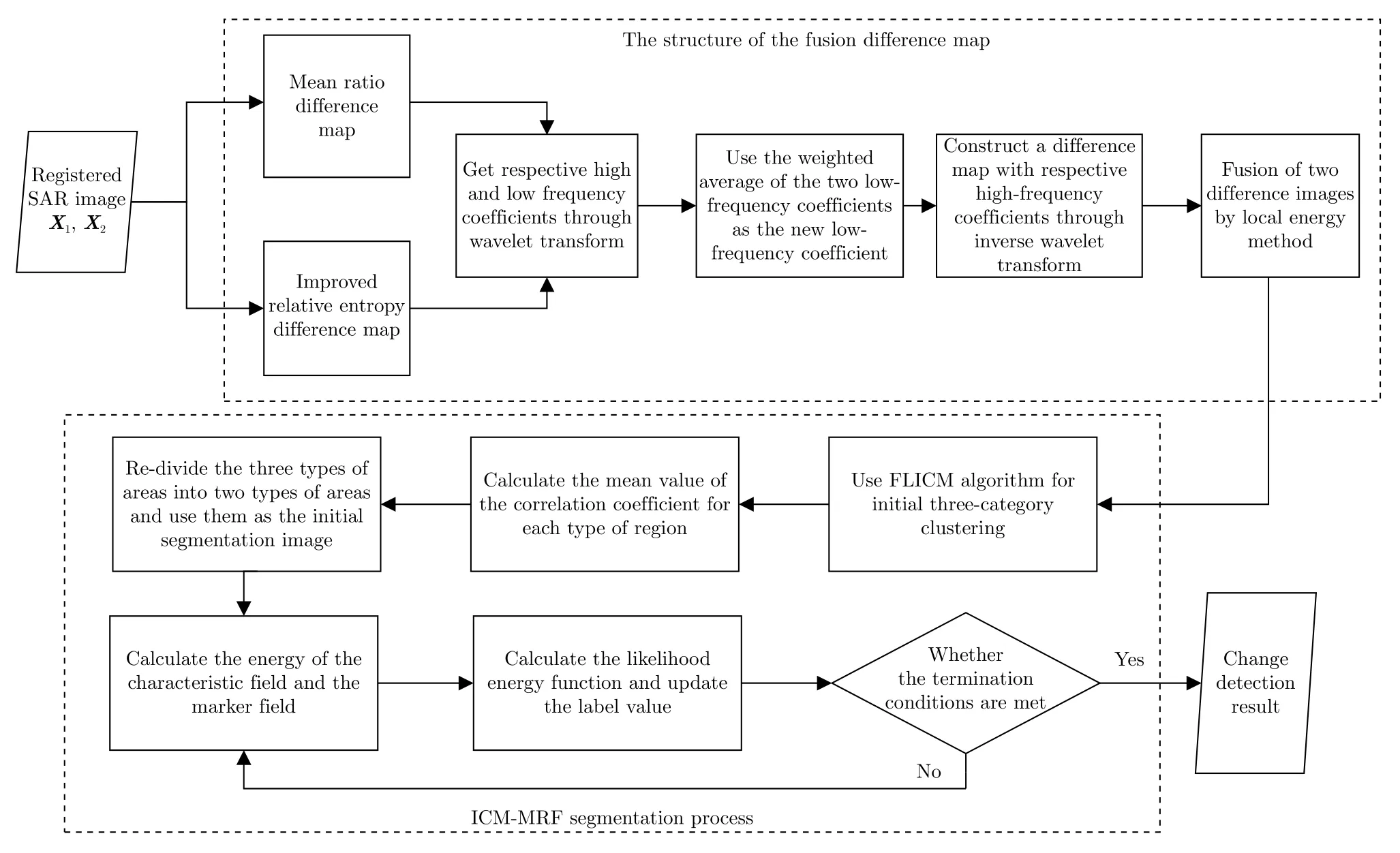
图1 基于融合差异图的变化检测算法流程图Fig.1 Flow chart of change detection algorithm in this paper

在相对熵的计算中引入像元空间邻域的异质性信息，突出图像边缘，增强连续性，同时抑制背景信息。邻域异质性信息可表示为

ℓ表示图像像元间的异质度，其定义为像元邻域的方差δ(x)和其邻域的均值µ(x)的比值。则引入邻域异质性信息后的相对熵计算公式可定义为

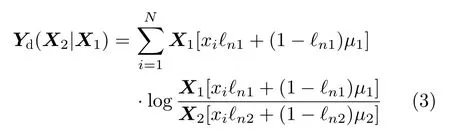
其中，Yd为X2对X1的邻域异质性相对熵，ℓn1,ℓn2分别为图像X1,X2同一位置像元对应的异质性系数归一化后的结果，µ1,µ2为其分别对应的去除中心像元点的邻域均值

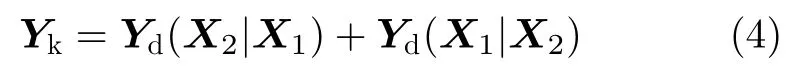
式(4)为相对熵计算的对称性处理，Yk为本文改进的相对熵差异图的最终结果。使用邻域异质信息来调节图像相对熵的计算，熵值越小表示两幅图像同一位置对应像元的相似程度越高，反之则相似程度越低。

引入邻域异质性信息的相对熵计算方法，相对于传统的单一像元值的熵值计算方法，有较好的背景抑制和边缘连续性效果，但目标区域的完整性和平滑性一般，故将目标区域完整性和平滑性较好的均值比算子差异图与本文引入邻域异质性信息的差异图，通过小波变换进行融合。均值比算子可定义为

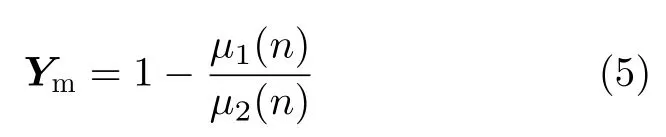
其中，µ1(n)和µ2(n)分别表示在图像X1和X2第n个像元其邻域(一般取3×3大小)内的平均值，Ym表示均值比差异图。

本文图像通过小波变换进行融合，小波变换一般先将图像分解为更低分辨率水平上的低频轮廓信息，以及在水平垂直和对角线方向的高频细节信息，再经过小波系数的替换、选择权值或者叠加运算进行融合。本文选择的融合规则如下：(1)取两图像小波分解后的加权低频系数均值作为新的低频系数；(2)将新的低频系数与各自的高频系数经小波逆变换得到融合低频系数后的差异图；(3)将两幅新的差异图通过局部能量法得到目标差异图。经过本文规则得到的差异图中，具有均值比差异图中较好的区域完整性和平滑性，也具有改进相对熵差异图中背景抑制性较强、边缘连续性较好的优点。

2.2 ICM-MRF分割

FLICM是一种无监督的模糊聚类算法，通过图像的统计特性可以较好地完成分类，进而提取图像的变化信息。使用FLICM算法将融合差异图分为两类的目标函数为

若以µn1和µn2分别表示为第n个像元对于两类的隶属度，通过比较两类的隶属度大小，则可以确定初始分割结果。

通过FLICM算法将差异图分为3类，分别代表变化区域、待定区域以及未变化区域。计算洪灾前后两SAR图像的相关系数，如式(10)所示

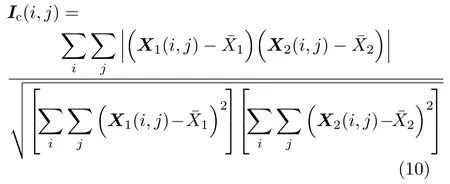
式中，Ic(i,j)表示为(i,j)像元点对应的相关系数值；X1(i,j)和X2(i,j)均表示图像的(i,j)像元点对应的像元值；表示X(i,j)像元点周围邻域像元值的均值。计算各类区域相关系数均值，比较待定区域相关系数与变化区域和未变化区域相关系数的均值，进行二次分类。

融合差异图通过以上算法二次分类后，其结果可作为ICM-MRF算法的初始分割。假设融合差异图像为Y={yη=yij}，初始分割图像X={xη=xij}为定义在Y上的马尔科夫随机场，是对图像所做的标记；xη是点η的类别标记，xη ∈I(I=1,2,···,k),k为类别数，本文中k=2。设点η的邻域值记为sη,s={sη,η ∈Y}是η的邻域系统。求解最优图像标记问题的关键在于求解先验概率P(X)和概率密度函数P(Y |X)。基于贝叶斯决策理论以及马尔科夫随机场和吉布斯分布的等价性，选取2阶邻域系统和合适的模型，用β表示马尔科夫参数，则局部条件先验概率可表示为

Vh为使用Potts数学模型的基团势能函数，H为所有基团的集合。由于要得到后验概率P(X|Y)最大，即等效于求解U(X|Y)最小，采用迭代条件模型(Iterative Conditional Model,ICM)求解，它的核心思想是用逐像元点最大化条件概率，迭代地实现每个像元点的更新，如式(15)所示

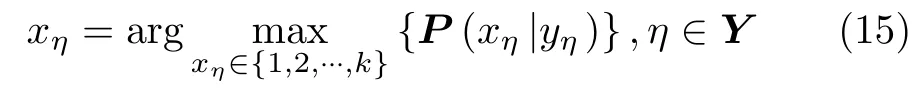
在马尔科夫随机场(Markov Random Field,MRF)算法中，作为初始分割的标签图对MRF的分割结果有较大的影响，因此将利用图像相关性对FLICM算法二次分类后的结果作为MRF算法的初始标签图，以期得到更好的初始分割结果，则基于融合差异图的ICM-MRF算法如表1所示。

3 实验结果与分析

本文选择的验证数据为瑞士Bern地区在1999年4月和5月的ERS-2数据，两时相遥感图像为图2(a)、图2(b)，大小为301×301，变化检测参考图为图2(c)；加拿大Ottawa地区在1997年5月和8月的Radarsat遥感数据，两时相遥感图像为图3(a)、图3(b)，大小为290×350。两数据集产生图像变化的主要原因均为洪水淹没陆地所致[2]。

表1 基于融合差异图的ICM-MRF图像分割计算过程Tab.1 ICM-MRF image segmentation calculation process based on fusion difference map

使用上述数据进行仿真试验，通过对Bern地区数据以及Ottawa地区数据均值比、相对熵方法得到的差异图，以及本文融合差异图进行比较，得到了上述所有方法在两数据集下不同差异图的期望最大化(Expectation-Maximization,EM)算法、K-means算法、FLICM算法以及本文ICM-MRF算法的检测结果，并分别在两数据集下进行主观和客观的评价。其后通过本文方法对2020年中国鄱阳湖地区数据进行变化检测，进而估计由于鄱阳湖湖水覆盖而受灾的区域面积和变化趋势。

本文采用虚警率(False Positive,FP)、总错误率(Overall Error,OE)、准确率(Probability Correct Classification,PCC)和Kappa系数作为量化评估的指标。其中，PCC表示总体的分类正确性，Kappa系数综合考虑了像元点的检测状况，是衡量检测精度的关键指标，其值越大表示检测精度越高。

3.1 差异图2分类和3分类影响分析

Bern地区数据集的不同算法差异图如图4(a)—图4(c)所示，并以A表示均值比差异图，B表示相对熵差异图，C表示本文差异图，在此3种差异图下，以EM算法、K-means算法和FLICM算法为例，分析了2分类和3分类后基于相关系数二次分类对结果的影响，如图5、图6和图7所示。对比各算法的差异图可得，均值比算法在背景中存在大量噪声，相对而言，相对熵法虽大量抑制了噪声，但模糊了目标区域的结构。本文构造的差异图综合了相对熵和均值比差异图的优势，边缘连续性和区域完整性较相对较好，与背景的对比度较两差异图更为明显，且噪声点较均值比差异图更少。从以下变化检测结果图中不难看出，当仅将差异图划分为2类时，噪声点和一些区域也将直接定义为变化区域或者为变化区域，直接影响了结果的区域划分和检测精度。而将差异图先划分为变化区域，未变化区域以待定区域3类区域，再将其根据不同划分区域的相关系数二次分类后，将有效地减小噪声的影响，并加强了区域的完整性，进而提升检测结果的精度。相对于均值比和异质相对熵差异图，在不同算法下，本文差异图也显示了更好的分类效果。

图2 Bern地区数据Fig.2 Bern region data

图4 Bern数据差异图Fig.4 Bern data difference map

图5 基于均值比差异图2分类和3分类后二次分类结果Fig.5 Based on the difference map in mean ratio 2 and 3 classification results after secondary classification

图6 基于相对熵差异图2分类和3分类后二次分类结果Fig.6 Based on the difference map in relative entropy 2 and 3 classification results after secondary classification

3.2 Bern和Ottawa地区实验结果与分析

Bern地区数据集对应的每种差异图的不同算法变化检测结果的相关指标分析如表2所示。对于不同差异图Bern数据集的本文算法变化检测结果如图8(a)—图8(c)所示。检测结果中白色点为变化区域的像元点。从变化检测结果图中也可看出，在本文ICM-MRF算法下，融合差异图的检测结果显示了更好的变化区域边界，与实际的变化情况更为接近。表2中也显示了针对不同差异图下同一种算法的变化检测结果，本文差异图相对于其他差异图而言，具较低的虚警率与总错误率，更高的正确率和Kappa系数。针对本文差异图而言，由于EM算法检测结果中存在较多噪声，故Kappa系数较低，但仍可看清变化区域的完整结构，并且本文ICM-MRF算法具有更高的Kappa系数和较低的错误率，相对于检测效果较好的FLICM算法，Kappa系数提高至0.837。

图7 基于融合差异图2分类和3分类后二次分类结果Fig.7 Based on the fusion difference and the results of secondary classification after classification 2 and 3

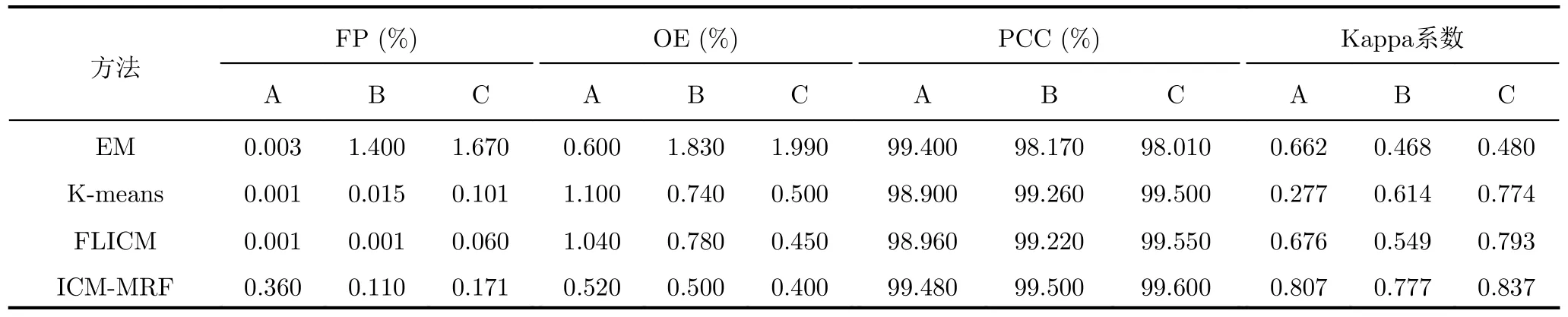
表2 Bern数据集不同差异图不同算法变化检测指标分析Tab.2 Analysis of change detection indicators of different algorithms in Bern dataset

图8 Bern数据本文ICM-MRF算法变化检测结果Fig.8 Change detection results of this paper algorithm in Bern data

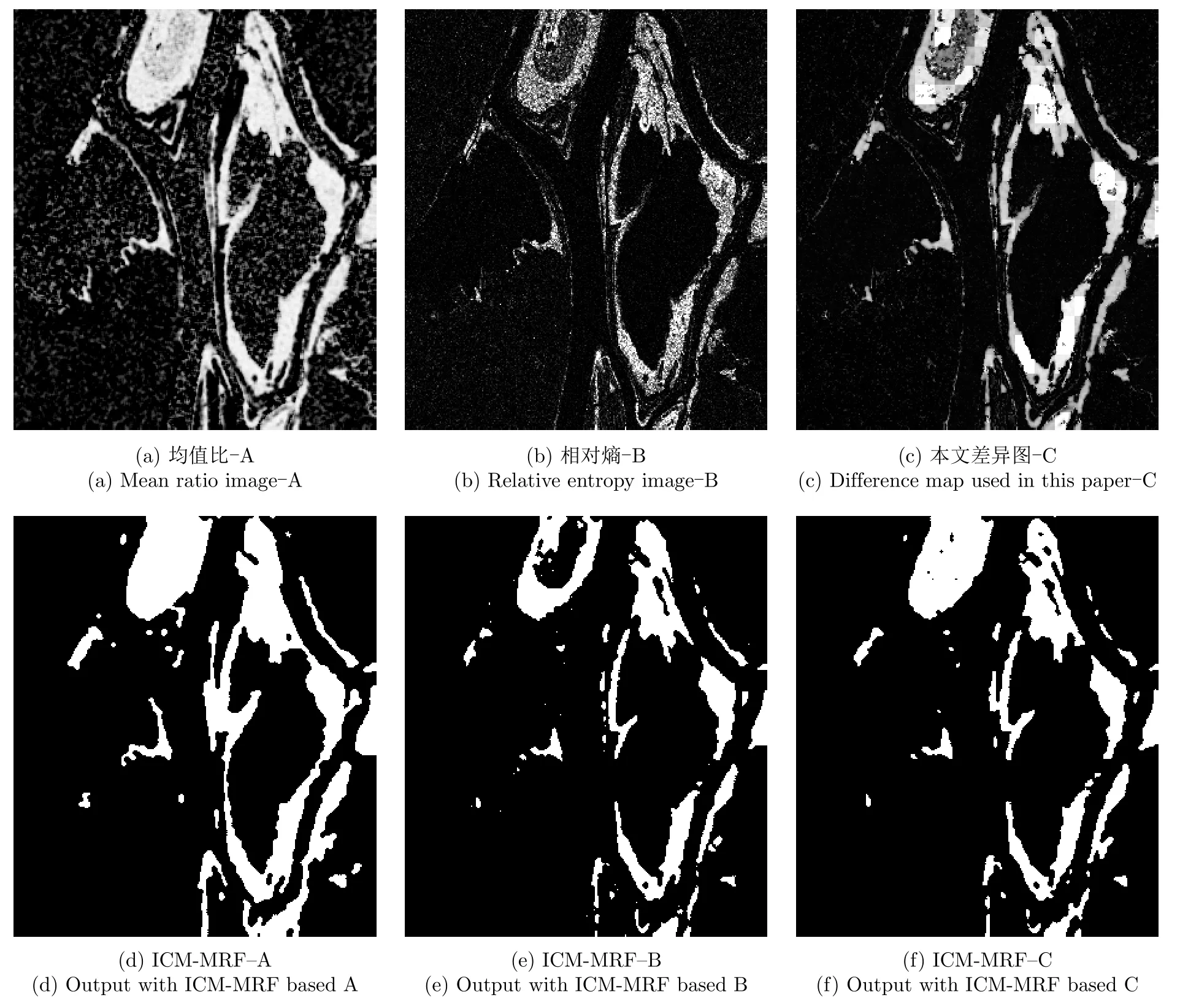
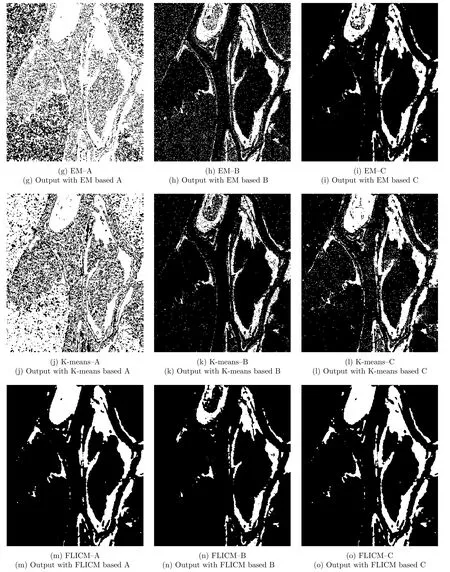
图9 Ottawa数据差异图及其变化检测结果Fig.9 Ottawa data difference map change detection result

Ottawa地区数据集的不同算法差异图如图9(a)—图9(c)所示，并以A表示均值比差异图，B表示相对熵差异图，C表示本文差异图，其对应的每种差异图的不同算法变化检测结果的相关指标分析如表3所示。对于不同差异图Ottawa数据集的本文ICM-MRF算法变化检测结果如图9(d)—图9(f)所示，EM算法变化检测结果如图9(g)—图9(i)所示，K-means算法变化检测结果为图9(j)—图9(l)所示，FLICM算法变化检测结果为图9(m)—图9(o)所示。检测结果中白色点为变化区域的像元点。通过对比各算法的差异图不难看出，均值比算法、相对熵算法与Bern区域结果分析一致，且本文的差异图构造方法在Ottawa数据集内也体现出边缘连续性，区域完整性以及背景对比度均相对较好的效果。不同差异图的变化检测结果中，构造的融合差异图在本文ICM-MRF算法下变化检测结果相对于均值比差异图的检测结果具有更好的细节表现，而相对于相对熵差异图的检测结果具有更好的区域完整性，且Kappa系数也有一定提升。表3中也显示了与Bern数据集基本相似的指标分析结果，由此可见本文算法在两数据集均具有较好的适用性。整体而言，本文算法可以提高变化检测结果的精度，减小错误率。

3.3 鄱阳湖区域洪灾前后变化检测结果分析

由于连续多日暴雨的影响，中国鄱阳湖区域发生洪灾，淹没了周边大片陆地区域，人工无法有效地实时实地测量受灾区域而制订善后处理计划，利用SAR卫星遥感图像，可以快速准确地提取受灾区域，评估灾区的空间分布和动态变化。本文选取中国鄱阳湖地区2020年6月和7月Sentinel-1-A数据进行实验来评估此次洪灾。由于完整的鄱阳湖区域分布在Sentinel-1-A数据的两景图像内，故本文使用对两景数据分别检测的方法进行实验。具体实验数据为2020年6月26日数据，拼合后完整鄱阳湖区域图像如图10(a)所示，7月8日数据如图10(b)所示，7月20日数据如图10(c)所示，3日包含鄱阳湖整体区域的Sentinel-1-A数据。图10(a)、图10(b)和图10(c)大小均为999×651，像素大小为243×243 m2，产生图像变化的主要原因是鄱阳湖水淹没附近区域陆地所致。

通过EM算法、FLICM算法、K-means算法和本文ICM-MRF算法，在融合差异图下对鄱阳湖Sentinel-1-A卫星遥感图像进行变化检测，EM算法变化检测结果如图11(a)、图11(b)所示，FLICM算法变化检测结果如图11(c)、图11(d)所示，K-means算法变化检测结果如图11(e)、图11(f)所示，本文ICM-MRF算法变化检测结果如图11(g)、图11(h)所示。通过对比6月26日与7月8日的变化检测结果，明显看到在本文差异图下两种算法均有较好的检测结果，得到的变化区域也较为相似，但不同的是，在图11(c)、图11(d)的FLICM算法中，黄色方框区域为虚警区域，此区域在真实雷达图中并未被洪水淹没，图11(a)、图11(b)EM算法和图11(e)、图11(f)K-means算法中，黄色方框区域为漏警区域，此区域为被洪水淹没的区域，而本文算法均未将两区域错误划分，整体来看，本文算法下，变化区域结构更为完整，检测结果更为准确。

基于本文算法，图11(g)—图11(j)变化检测结果为3幅鄱阳湖洪灾前后变化检测结果。其中，图11(g)为6月26日与7月8日的变化检测结果，图11(h)为其对应在实际中的变化区域。图11(i)为7月8日与7月20日的变化检测结果，图11(j)为其对应在实际中的变化区域。白色、红色和蓝色像元点代表变化区域。由此可见，本文算法较完整且清晰地检测出鄱阳湖区域的洪灾前后变化范围。选取的包含完整鄱阳湖区域的SAR图像实际面积约为38402.46 km2，由于受暴雨影响，鄱阳湖水位上升，7月8日—7月20日，鄱阳湖西南部区域受灾严重，湖水淹没了湖周边大片陆地，包括附近水域淹没的水中小岛和陆地等。由表4鄱阳湖区域变化检测结果量化分析可知，此期间变化像素数为12589，占总像素点的1.94%，总体受灾面积大约为 743.37 km2。7月8日—7月20日，在表4中仍可看到5475个变化像素点，占总像素点的0.84%，这表明总体受灾面积仍在提升，但变化像素点减少了大约56.5%，洪水淹没区域较之前明显减少，期间总受灾面积大约为323.29 km2，洪灾扩散势头逐渐减小。值得注意的是，图11(j)中蓝色区域虽为变化区域，但不是洪水淹没区域，而是由水体转为陆地的区域，这也说明部分区域的洪水被引流或者逐渐退去，总体形趋于稳定。

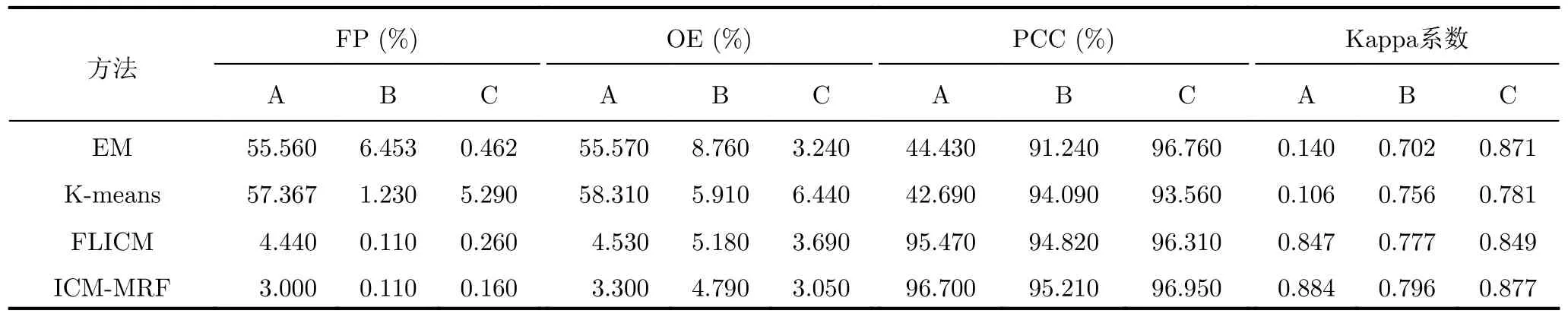
表3 Ottawa数据集不同差异图不同算法变化检测指标分析Tab.3 Analysis of change detection indicators of different algorithms in Ottawa dataset

图10 鄱阳湖地区数据Fig.10 Poyang Lake area data

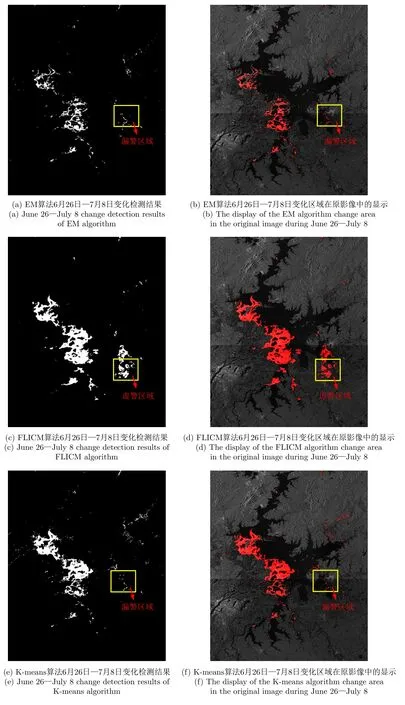
图11 鄱阳湖区域EM,FLICM,K-means和本文算法洪灾前后变化检测结果Fig.11 Change detection results of EM,FLICM,K-means and this paper algorithm before and after the flood disaster in Poyang Lake area

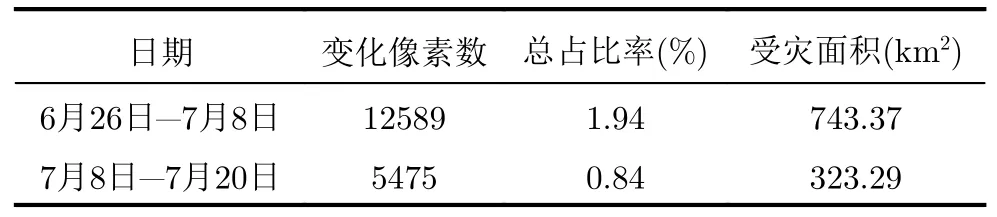
表4 鄱阳湖区域变化检测结果量化分析Tab.4 Quantitative analysis of the detection results of Poyang Lake area change

4 结论

针对洪灾区域的变化检测，本文提出一种基于融合差异图的变化检测方法，利用邻域异质性信息保持相对熵差异图中变化区域的连续性，抑制背景信息，并通过小波变换，构造与均值比差异图融合的最终差异图。通过FLICM聚类算法与图像的相关系数结合而得到更接近于洪灾变化区域的二次分类结果，然后将其经过ICM-MRF算法优化得到最终的变化检测结果。在Bern地区ERS-2遥感数据以及Ottawa地区Radarsat遥感数据实验结果均表明，本文方法对洪灾区域的变化检测结果有较好的检测精度，变化区域结构更为完整准确。通过本文算法得到2020年6,7月份中国鄱阳湖地区的3景Sentinel-1-A遥感图像变化检测结果，并对其受灾区域面积以及变化趋势进行估计，具有一定的实用价值。今后将继续研究洪灾区域产生虚警、漏警的原因以及在变化检测中自动区别洪水淹没区域和水体转为陆地区域的方法。