基于邻域一致性的极化SAR图像仿射配准

朱庆涛 殷君君 曾 亮* 杨 健*

①(清华大学电子工程系 北京 100084)

②(北京科技大学计算机与通信工程学院 北京 100083)

1 引言

合成孔径雷达(Synthetic Aperture Radar,SAR)全天时、全天候、高分辨率成像的特点使得它在环境监测、资源探测、战场感知等方面具有重要的战略意义。近年来，多时相、多波段、多成像模式下的SAR图像资源日益丰富。它们的融合处理对于遥感目标的检测、识别等任务具有重要意义。而SAR图像之间的配准则是上述融合处理的基础，需要具有良好的精度与速度。当前的配准算法主要是基于极化SAR图像的散射强度、极化特征等信息，结合相似性度量与参数迭代估计来实现。随着深度学习的发展，基于深度神经网络的极化SAR图像配准算法也逐渐增加，但是主要还是结合图像块的特征匹配与图像变换参数的迭代估计来实现[1,2]。目前尚未提出基于深度卷积神经网络的端到端极化SAR图像一步配准算法。

受到光学图像处理领域中基于深度学习的端到端特征匹配算法的启发，本文提出了一种无需对图像进行切块处理或参数迭代估计的端到端极化SAR图像配准算法框架。首先，对输入图像对进行特征提取，并进行k近邻特征匹配。之后，通过4D稀疏卷积网络，基于邻域一致性原则实现特征匹配的过滤。最后，根据输出的匹配点对置信度，利用带权最小二乘法进行仿射参数的一步回归，实现图像对的配准。

本文的结构组织如下：第2节对极化SAR图像配准算法进行综述。第3节讨论本文提出的配准算法。第4节给出实验结果与分析讨论。第5节为结论。

2 极化SAR图像配准方法

2.1 基于传统方法的极化SAR图像配准

传统的图像配准方法主要分为两类，一类是基于区域的方法，另一类是基于特征的方法。基于区域的方法主要是通过寻找与模板窗口具有较高相似性的图像块来求解最佳匹配参数。常见的有归一化互相关法[3]，Kullback-Leibler散度法[4]，互信息法[5]，傅里叶变换域法[6]等；基于特征的方法则主要是通过检测两幅图像中的显著特征点，根据周围像素点生成特征描述符后，基于欧氏距离等度量来进行匹配。之后通过随机抽样一致性(Random Sample Consensus,RANSAC)等迭代估计的方法获取可靠匹配点对以确定变换参数。常见的有基于Harris[7],SIFT (Scale-Invariant Feature Transform)[8]等的配准算法。以基于SIFT的配准算法为例，首先构建高斯金字塔与差分高斯金字塔，在多尺度空间内进行极值点检测；之后对关键点进行精细定位并分配方向，同时筛除不稳定的关键点；结合上述关键点位置、尺度与方向信息，得到关键点的128维特征描述向量后，设定最近邻与次近邻距离比阈值，筛除不显著的匹配点对。最后使用RANSAC算法对匹配点对进行精细筛选，从匹配结果中选取几对进行全局变换参数求解，实现图像配准。相比于基于区域的配准，基于特征的配准方法具有更好的鲁棒性，但是具有较高的计算复杂度。

上述图像配准算法被广泛应用于极化SAR图像配准。在基于区域的配准方面，研究者结合极化SAR图像的散射特性对相似性度量进行重新设计[9]；在基于特征的配准方面，提出了基于极化SAR图像特性的改进SIFT配准算法SAR-SIFT[10],PSO-SIFT[11]等。SAR-SIFT算法中考虑到极化SAR相干斑噪声的特点，结合SIFT与Harris关键点检测算法的优势，采用SAR-Harris空间代替高斯差分金字塔，使得Harris检测算子具备尺度不变性。该算法能够有效地对SAR图像的角点特征进行提取，实现了针对SAR图像的精细配准。

2.2 基于深度学习的极化SAR图像配准

(1) 深度卷积神经网络

近年来，随着计算机存储与计算能力的提升，深度学习在计算机图像处理领域取得了较大的进展。深度卷积神经网络通过权重共享的卷积层对图像特征进行自动提取，具有良好的特征表达能力与泛化性能，被广泛应用于图像检测、识别、分割等领域。2012年，AlexNet[12]获得ImageNet竞赛冠军后，各种优秀的深度卷积神经网络结构被不断提出。随后深度卷积神经网络逐渐被运用于极化SAR图像处理中。相比于传统方法，深度学习在极化SAR图像的各个应用领域中表现出较强的优越性，例如徐丰等人[13]利用深度卷积神经网络进行极化SAR目标识别与地物分类，Jin等人[14]提出了一种基于深度学习的极化SAR舰船目标检测算法。

(2) 基于深度学习的图像配准

随着深度学习的发展，卷积神经网络逐渐被运用到图像配准领域，算法主要分为3类。一类是利用深度卷积神经网络替代人工特征提取，之后仍然通过RANSAC等迭代估计的方式完成变换参数求解与图像配准。另一类是利用深度卷积神经网络通过有监督学习的方式直接对变换参数进行回归。例如DeTone等人[15]通过卷积神经网络对生成的仿真图像对进行有监督学习，实现单应性矩阵的直接回归，从而实现图像配准；Rocco等人[16]利用深度神经网络来模拟传统配准过程中的特征提取、匹配与参数回归。首先，利用深度卷积神经网络进行特征提取。之后，通过内积操作来得到特征图的相关度信息。最后，通过全连接层进行参数的有监督回归。但是由于特征图分辨率较低，导致算法的配准精度不高。还有一类是利用深度卷积神经网络对变换后的图像与目标图像的相似性进行优化，通过无监督学习的方式实现图像的配准。例如Balakrishnan 等人[17]通过无监督学习的方式优化变换图像与目标图像的局部相关性与平滑性来实现医学图像的配准；在文献[16]的基础上，Rocco等人[18]利用无监督学习的方式来增加特征图匹配点对的一致性，提出了基于局部邻域一致性的密集4D卷积结构来筛选稳定的特征匹配点对。然而由于内存的限制，匹配的精度依旧较低。后续工作中，他们通过稀疏卷积神经网络很大程度上节省了内存，使得高分辨率、高精度的图像对的关键点匹配得以实现，不过未实现后续的图像配准[19]。

(3) 基于深度学习的极化SAR图像配准

基于深度学习的极化SAR图像配准算法主要利用深度神经网络直接预测图像块是否匹配或将深度卷积神经网络作为特征自动提取器，之后仍然需要利用RANSAC等迭代算法进行变换参数求解。文献[1]基于SIFT算法对图像的关键点进行定位，提取关键点周围的图像块，并通过自监督学习的方式训练了一个能够预测图像块是否匹配的深度神经网络。最后基于粗匹配结果利用RANSAC对变换参数进行迭代估计；文献[2]基于VGG16卷积神经网络对遥感图像进行特征提取，并基于欧氏距离对特征描述符进行预匹配。最后基于动态内点筛选算法对变换参数进行迭代估计。总之，现有的方法均考虑对大场景的SAR图像进行切块处理后，基于图像块进行独立的粗匹配，未考虑块间匹配的关联性。因此往往需要进行参数迭代估计的后处理步骤来筛除错误的匹配，从而得到精确的变换参数。上述方法中预处理与后处理的引入使得配准流程较为烦琐费时。目前尚未提出根据极化SAR待配准图像对，基于深度卷积神经网络的输出结果直接实现一步配准的端到端算法框架。

本文借鉴了文献[19]的思路，将邻域一致性与稀疏卷积神经网络应用于极化SAR图像配准中，实现了一种采用弱监督学习的端到端极化SAR图像一步配准的算法框架。该算法无需对输入图像对进行切块预处理或是参数迭代估计，配准精度较高且速度较快。

3 基于邻域一致性的SAR图像配准

3.1 整体框架

该配准算法主要由特征提取、特征稀疏匹配、特征匹配过滤与参数估计4个部分组成。如图1所示，特征提取模块用于提取输入图像对{IA,IB}的特征信息{fA,fB}，采用的网络结构借鉴了DenseNet网络结构[20]。特征图fA的坐标系为i-j，特征图fB的坐标系为p-q。特征匹配模块根据特征图{fA,fB}，采用归一化内积的方式(即余弦距离)对特征点对的相关度进行求解。为了保留更为显著的特征对以及节省内存，特征匹配模块对每个特征点仅保留k个相关度最高的匹配点，由此可以得到4D的特征粗匹配稀疏相关图(Sparse Raw Correlation Map)SRAB。特征匹配过滤模块中通过4D稀疏卷积网络对SRAB中非零元素的邻域进行卷积滤波操作，输出过滤后的4D稀疏相关图(Sparse Filtered Correlation Map)SFAB中的每个非零像素SFAB(in,jn,pn,qn)的值代表了特征匹配点对{(in,jn)}与{(pn,qn)}的匹配置信度，其中n为某一匹配点对的标号。变换参数回归模块根据置信度较高的N对匹配点对坐标{(in,jn)}{(pn,qn)}(n=1,2,···,N)以及它们的匹配置信度{sn}通过带权最小二乘法回归出仿射变换参数进行图像配准。

3.2 特征提取模块

文献[19]中采用了ResNet网络结构作为骨干网络来提取输入图像对的特征。本文则采用Dense-Net结构对输入图像对{IA,IB}进行特征提取。为了便于特征图的下采样，DenseNet采用了多个DenseBlock连接的方式。每个DenseBlock内部通过特征级联的方式建立了卷积层之间更加密集的连接。如图2所示，DenseBlock模块内的主要卷积单元为BN-ReLU-Conv的串联，其中BN (Batch Normalization)为批归一化层，ReLU (Rectified Linear Unit)为线性整流激活层，Conv为卷积层。由于特征级联操作会改变特征图尺寸，因此在每个卷积单元后面添加了1×1卷积层进行特征降维操作，将输入卷积单元的特征图通道数进行统一。在DenseBlock中，每个卷积单元的输入特征图为之前所有卷积单元的输出特征图的级联，最后一个卷积单元的输出特征图作为Transition层(包含1×1卷积层以及2×2池化层)的输入。

相应的数学表达如式(1)所示

式中，xt表示DenseBlock内第t个卷积单元的输出特征图，Ht表示1×1特征降维与第t个卷积单元对应的操作，它的输入为前t个(0,1,···,t–1)卷积单元输入特征图x0,x1,···,xt−1的级联。特征的充分复用使得网络的特征表达能力十分出色，对于局部信息的描述更加细致。

对于常见的深度卷积神经网络结构GoogleNet,ResNet,DenseNet等，深层特征图的分辨率较小，代表着图像较为抽象的语义特征，图像边缘、纹理等特征信息则较为模糊；而浅层特征图的特征信息提取不够充分。仿射配准任务并非目标识别或场景理解等高级别的任务，在利用深度卷积神经网络进行特征提取时，需要尽可能保留较多的图像边缘、纹理信息，同时也需要较为充分的特征提取，因此特征提取网络的结构深度应避免过深或过浅。本文将第3个DenseBlock的输出特征图作为特征提取模块的输出结果。以1200×1200×3的输入尺寸为例，特征提取网络与每层输出的尺寸如表1所示。表中conv卷积单元包含了BN-ReLU-Conv。

图1 基于邻域一致性的SAR图像配准算法框图Fig.1 Flowchart of image registration based on neighborhood consensus

图2 DenseBlock的网络结构Fig.2 Structure of DenseBlock

3.3 k近邻特征稀疏匹配模块

记经过特征提取模块得到的特征图分别为fA和fB(fA,fB∈Rm×Rm)。对于特征图fA的某一个坐标点(i,j)，计算该点与fB所有坐标点的特征值内积并进行归一化来作为特征的相关系数(相当于采用余弦距离来替代欧氏距离)，仅保留k个与fA(i,j)的特征相关值最大的坐标点fB{(p1,q1),(p2,q2),···,(pk,qk)}。最终得到k×m×m个相关值，可理解为稀疏的单通道4D图像SRA→B(该4D图像的4个坐标值是fA的(i,j)和fB的(p,q)，像素值为归一化的相关值)。记上述操作为特征图A对特征图B的单向k近邻操作。由于上述操作并非全图互相关操作，因此特征图A对特征图B进行单向k近邻得到的图像SRA→B与特征图B对特征图A进行单向k近邻得到的图像SRB→A并不一定相同。以k取2为例，设特征图B中与特征图A上点(i1,j1)的相关度最高的2个点分别为(pu,qu)和(pv,qv)，相关值分别为r1u和r1v。而特征图A中与图B上点(pu,qu)相关度最高的2个点中却未必包含点(i1,j1)。为了进一步增强双向均近邻的匹配点对的相关性，抑制仅单向近邻的匹配点对的相关性，将两个4D的稀疏单向k近邻相关图进行叠加，得到稀疏的4D粗匹配相关图SRAB作为特征匹配模块的输出结果。

3.4 特征匹配过滤模块

本文涉及的邻域一致性原则是指由于极化SAR图像对应的自然场景具有较高的局部空间连续性，故稳定的显著特征点对附近应该还存在一些匹配程度较高的点对，否则该点对的匹配置信度应大幅削减。通常的卷积神经网络为密集卷积操作，给定卷积核，通过参数共享，对整幅图像(或中间特征图)进行滑动卷积操作，会遍历图中每一个像素。当图像(或特征图)为稀疏图，即大部分像素值为零时，仅需要遍历非零元素进行卷积操作即可。稀疏张量自动微分库Minkowski Engine[21]实现了通用的稀疏卷积操作，在输入稀疏图非零元素的索引与像素值后，可以对非零元素进行遍历并进行局部卷积操作。由于配准图像训练集较小，因此稀疏卷积网络部分的层数设计得较小，仅为2层，第1层的输出通道数为16，第2层的输出通道数为1，卷积核大小均为3×3，即仅考察目标匹配点对周围3×3的邻域信息。

基于上述网络结构，设计损失函数以驱动网络学习对输入的4D粗匹配相关图SRAB进行邻域滤波的能力。损失函数如式(2)所示

式中，函数F()代表深度卷积神经网络，xpos代表了一对正样本图像(场景相关联，可以进行配准的图像对)，xneg代表了一对负样本图像(场景无关联，无法进行配准的图像对)。卷积神经网络F()接收了一对图像对之后，输出结果为4D稀疏相关图，图上非零元素代表了特征图匹配点对的置信度大小。代表了对4D稀疏相关图的非零元素进行求和的操作。损失函数的值L设计为负样本对的输出置信度之和与正样本对的输出置信度之和的差。根据Loss的第2项，对于负样本对输入，理论上大多数匹配点对为不稳定点对，在Loss下降的过程中，网络参数的优化方向是抑制所有输出点对的置信度，因此网络在这个过程中学习到了抑制不稳定匹配点对的能力；根据Loss的第1项−，对于正样本对输入，理论上存在许多匹配点对为稳定点对，在Loss下降的过程中，网络能够使得正样本对的输出置信度之和尽可能大，即学习到了增强稳定匹配点对的能力。二者相结合，构成的联合Loss即为最终的损失函数。综上所述，特征匹配过滤模块能够增强稳定匹配点对的置信度，抑制不稳定匹配点对的置信度。记滤波后的4D稀疏匹配相关图为SFAB。

表1 特征提取模块的结构Tab.1 Structure of the feature extraction module

3.5 基于带权最小二乘法的参数回归

由4D稀疏匹配相关图SFAB可以得到图像fA和fB的稳定匹配点对，之后按照网络输出的置信度{sn}的大小，选取前N个坐标点对进行仿射变换参数求解。由于当前的匹配点对本身具有较好的稳定性与一致性，因此无需进行类似RANSAC等算法的迭代参数估计，仅通过最小二乘法即可对变换参数实现准确估计。由于不同的点对具有不同的置信度，因此采用带权最小二乘法进行仿射变换参数回归。通用的带权最小二乘回归原理如式(3)所示

其中，θ为待定参数；(X,Y)为一对观测量；W为每个观测样本的权重构成的对角矩阵。

在对本文的仿射变换参数进行回归时，θ即为待求的仿射变换参数；(X,Y)为待配准图像fA和参考图像fB上置信度s最高的N对坐标点对；W可根据{sn}(n=1,2,···,N)进行设定。实际进行计算时，由于X和Y的每个元素均为二维坐标向量，难以直接按照式(3)进行计算，因此需要进行如下的变形处理。

如图1所示，仿射矩阵共有6个参数待求，记θe=[A11;A12;A21;A22;A13;A23]。记X的第t个元素为Xt=(Xti,Xtj),Y的第t个元素为Yt=(Ytp,Ytq)。在不考虑权重矩阵W的情况下，仿射变换的关系式如式(4)所示。

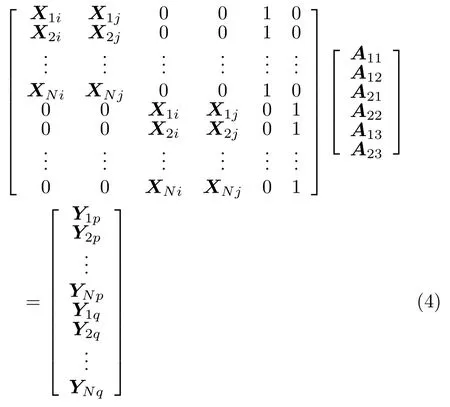
将式(4)中等式左边的第1个矩阵记为Xe，等式右边的矩阵记为Ye。之后，定义权重矩阵We=diag(s1,s2,···,sN)，其中diag()代表对角阵。最终按照式(5)带权最小二乘回归，得到仿射变换中6个待求参数的值。

4 实验与分析

4.1 实验环境与数据集

由于可用于配准的公开SAR图像数据集较为匮乏，且高分辨率的SAR图像与光学图像具有一定的相似性，故采用的训练数据集是Indoor Venues Dataset。训练方式为弱监督的方式，损失函数详见第3节。使用的显卡为单块GeForce GTX 1080Ti，处理器为Intel(R) Core(TM) i9-7920X。

为了进行对比试验，特征提取模块分别采用ResNet和DenseNet的架构进行对比，此外为了提高模型的收敛效果，均采用了ImageNet预训练模型进行微调。初步实验中，将k近邻稀疏匹配模块的参数k设置为10。后续讨论中考察了参数k的取值对配准性能的影响。特征匹配过滤模块采用两层4D稀疏卷积层。取最大的N=200个匹配置信度对应的点对作为稳定特征匹配点对。最后经过带权最小二乘法对仿射参数进行回归。将上述稀疏匹配与基于邻域一致性的过滤模块合起来记为Sparse Neighborhood Consensus Network (SNCNet)。实验中一共对比了5种不同的算法，分别是采用SIFT+RANSAC,SAR-SIFT+RANSAC,ResNet+SNCNet,DenseNet+SNCNet以及DenseNet+RANSAC。

图3 Wallerfing农田数据Fig.3 Wallerfing farmland data

图4 舟山港口数据Fig.4 Zhou Shan port data

用于测试的极化SAR待配准图像对如图3和图4所示。图3(a)和图3(b)分别为RADARSAT-2卫星于2014年5月28日和2014年6月10日获取的德国Wallerfing地区的农田图像，原始尺寸均为3000×3000，极化方式为HH,VV,HV和VH，采用精细全极化成像模式，中心频率为5.4 GHz(C波段)，像元大小为4.7 m×5.1 m，距离向分辨率为5.2 m，方位向分辨率为7.7 m，入射角为40.2°。图3(a)为升轨数据，图3(b)为降轨数据。将它们记为Wallerfing数据。图4(a)和图4(b)分别为PAZ卫星于2019年12月3日和2019年11月12日获取的中国舟山地区的港口图像，原始尺寸均为4000×4000，极化方式为HH,VV极化，分别采用聚束和条带成像模式，中心频率为9.7 GHz(X波段)，像元大小分别为1.5 m×1.5 m和2.75 m×2.75 m，距离向分辨率分别为3.1 m和6.0 m，方位向分辨率分别为3.5 m和6.1 m，入射角为51.1°。图4(a)为降轨数据，图4(b)为升轨数据。将它们记为舟山数据。在实验中，将用于测试的极化SAR图像对通过双线性插值缩放为1200×1200的大小。

4.2 评价指标

对待配准图像的仿射变换图像与参考图像按照不同的色彩通道进行叠加，可以得到配准叠加图，便于对配准算法进行直观评价。量化的评价指标则主要采用PCK (Average Probability of Correct Keypoints)[22]和APE (Average Pixel Error)，如式(6)和式(7)所示。设待配准图像A和参考图像B上已标注的N个点对为{PA,PB}i,i=1,2,···,N,wrap为仿射变换操作(所使用的仿射变换参数为第3.5节中得到的θe),d()代表两个二维坐标点之间的欧氏距离。阈值Lth=α·max(h,w)，其中α为人为设定的比例系数，h和w为待配准图像对的高与宽。

4.3 配准叠加图

首先从直观的角度对配准结果进行评价。采用本文的DenseNet+SNCNet算法，Wallerfing和舟山数据的仿射变换图像与目标图像的叠加图分别如图5(a)和图5(b)所示，两幅图中绿色的前景通道为待配准图像仿射变换的结果，紫红色的背景通道为目标图像。采用SAR-SIFT的实验结果如图6(a)和图6(b)所示。由图5和图6可以看到采用本文算法和SAR-SIFT算法，前景和背景的河流与海岸线等区域均能较好地重合，整体配准精度均较高。

4.4 量化指标结果分析

Wallerfing和舟山数据的APE如表2所示，采用不同配准算法的PCK曲线如图7(a)和图7(b)所示。

(1) 极化信息对配准效果的提升

由表2中Wallerfing数据的Pauli图像与Span图像的APE指标对比可知，极化特征的引入有助于提升配准精度。Wallerfing数据的Pauli图像如图3所示，对应的Span功率图如图8所示。Wallerfing数据中包含了种类丰富的农作物区域以及山地区域，同时还包含河流与湖泊区域。湖泊与河流等水域的后向散射强度较弱，在Pauli图像与Span图像中均呈现为稳定的黑色区域，而不同种类的农作物则具有各自独特的极化特性，后向散射强度分布比较复杂。

图5 DenseNet+SNCNet算法下，Wallerfing和舟山数据配准叠加图Fig.5 Overlay map of Wallerfing and Zhou Shan data by DenseNet+SNCNet

图6 SAR-SIFT+RANSAC算法下，Wallerfing和舟山数据配准叠加图Fig.6 Overlay map of Wallerfing and Zhou Shan data by SAR-SIFT+RANSAC

表2 各种配准算法的APE值Tab.2 APE of different registration algorithms

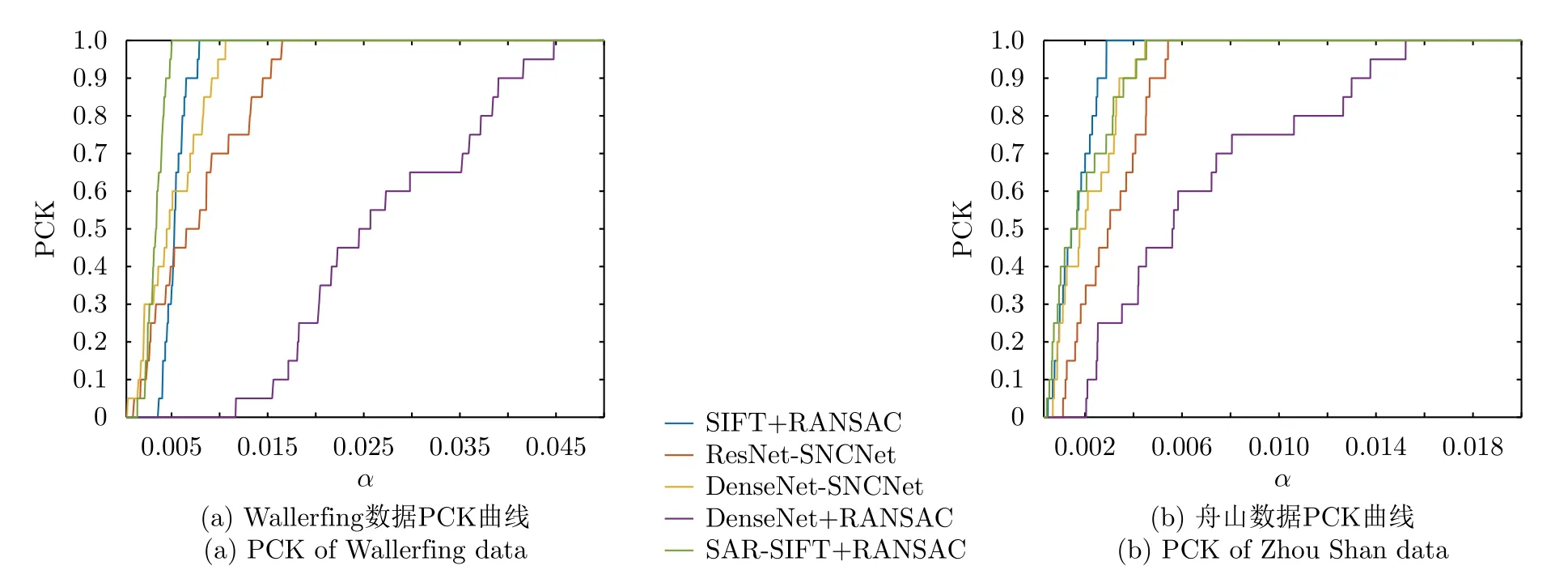
图7 不同算法下，Wallerfing和舟山数据配准的PCK曲线Fig.7 PCK of Wallerfing and Zhou Shan image registration with different algorithms

图8 Wallerfing农田数据Span图Fig.8 Span image of Wallerfing farmland data

在Pauli图中，不同农田区域具有明显的纹理特征，边缘信息较为明显，而在Span图像中，部分纹理与边缘信息缺失，对比度较弱。从APE指标可知，本文算法能够结合Pauli图像3个极化分解通道的极化信息，更好地利用极化SAR图像中的纹理、边缘等结构信息来实现图像的稳定匹配，相比于Span图像具有更加精确、稳定的配准效果。

(2) DenseNet特征提取的优势

由图7中Wallerfing与舟山数据配准结果的PCK值随α的变化曲线可知，本文所提算法相比ResNet-SNCNet具有一定的效果提升，配准精度与传统的SIFT+RANSAC与SAR-SIFT+RANSAC算法可以相媲美。

由表2中DenseNet-SNCNet与其他方法的APE指标对比可知，采用DenseNet特征提取结构的稀疏匹配效果优于ResNet，与传统的SIFT和SARSIFT算法精度相近，验证了DenseNet出色的特征表达能力。在1200×1200的分辨率条件下，Wallerfing数据和舟山数据的平均像素误差距离仅为6.175和2.553，平均像素误差距离与边长之比仅为6.175/1200=0.515%和2.553/1200=0.213%。

从网络结构的角度分析，DenseNet的DenseBlock中的特征密集连接与特征复用是它相比于ResNet的优势。ResNet的shortcut操作能够学习到网络的残差，在网络的层数较深时能够保证网络参数的学习更加流畅，有利于深层信息的传递与特征表达的学习。然而当前由于配准任务是较低层次的几何任务，因此特征提取的深度较浅，在该情况下，笔者认为ResNet的密集连接并未能够完全凸显其优势，而DenseNet的密集连接则能够更加充分地对图像低层次的特征进行表达，有助于后续匹配任务的进行。

为了进一步佐证DenseNet的显著特征提取能力，将输入图像对的分辨率修改为600×600，考察配准结果。如图9(a)和图9(b)所示，将输入的Wallerfing图像缩放为600×600时，DenseNet-SNCNet依然具有良好的配准结果，而ResNet-SNCNet出现明显的配准偏差，体现了DenseNet特征提取能力的优越性。

(3) 参数k对配准性能的影响

对于Wallerfing和舟山数据，采用DenseNet+SNCNet算法，在k值不同时，配准结果的APE和基于GPU的运算时间分别如表3和表4所示。

Wallerfing图像中存在具有一定重复性的农田纹理，且地形较为复杂，配准难度较高；而舟山港口图像中海域纹理比较单调，海岸线较为明显，故配准难度相对较低。由表3可知，对于复杂的配准图像，当k较大(例如16)时，4D稀疏匹配相关图的冗余信息较多，由于当前训练样本较少以及稀疏匹配网络结构设计较为简单，网络的配准性能相比于k较小时有明显下降；对于配准难度较低的图像对，k的选取对最终的配准性能没有太大的影响。

图9 600×600分辨率下，DenseNet-SNCNet和ResNet-SNCNet的配准结果Fig.9 Registration result of DenseNet-SNCNet and ResNet-SNCNet at 600×600 resolution

表3 k取不同值时，DenseNet+SNCNet配准结果的APE值Tab.3 APE of registration result by DenseNet+SNCNet with different k

表4 k取不同值时，基于GPU的DenseNet+SNCNet运算时间Tab.4 Time consuming of registration based on GPU by DenseNet+SNCNet with different k

由第3.3节对k近邻特征稀疏匹配模块的分析可知，单向近邻相关图存在k×m×m个非零相关值。理论上，由单向近邻相关图叠加后得到的4D粗匹配相关图SRAB中的非零元素个数一般会随着k的增加而增加。因此，稀疏匹配模块的参数量会随着k值的增大而增加，从而导致运算时间增加。由表4可知，k取16时的网络前向推断时间增加为k取2时的两倍左右。为了减少算法前向推断的时间，应尽量避免选择过大的k。

综上所述，为了提高算法的泛化性能，同时提高算法的运行速度，应尽量避免k取值过大，k的取值在2～10附近均较为合适。

(4) 特征匹配与过滤模块的有效性

DenseNet+RANSAC是用于验证特征匹配与过滤模块有效性的对照实验。从表2的APE值可以看到，利用DenseNet提取密集特征图并按传统方法基于欧氏距离度量进行次近邻粗筛后，利用RANSAC迭代算法进行仿射参数求解的效果劣于前述方法。可能的原因在于DenseNet进行特征提取后得到的是特征图的分辨率较低，利用传统的后处理方法，仅根据最近邻与次近邻的距离比进行粗筛，难以取得较好的粗匹配效果，因此即使进行RANSAC迭代估计，最终的匹配效果也较差。

图10 稀疏特征匹配过滤模块的有效性Fig.10 Effectiveness of the sparse filter module

为了进一步直观地体现特征匹配过滤模块的有效性，对输入特征匹配过滤模块前后的特征点对匹配以及显著特征点进行可视化。如图10所示，经过特征粗匹配得到的连线较为杂乱(仅选取了一部分匹配点对进行可视化)，而经过稀疏卷积过滤后的置信度较高的特征点对匹配具有较好的全局一致性。如图11所示，将特征匹配过滤模块输出的具有较高置信度的点对在图中标出。亮度越高的地方代表匹配置信度越高。该结果验证了本文算法能够有效地提取出河流、河岸与海岸线等在极化SAR图像配准任务中比较稳定的特征。

图11 显著特征点对的分布Fig.11 Distribution of salient feature pairs

(5) 算法时间分析

未进行算法并行化加速的SIFT类算法具有明显的时间劣势。传统的SIFT与SAR-SIFT算法的流程是构建高斯差分金字塔与SAR-Harris金字塔，进行关键点精细搜索，构建关键点特征描述向量，对特征进行次近邻筛选以及基于随机抽样一致性进行参数迭代估计。以SAR-SIFT为例，对于1200×1200的Wallerfing图像，构建SAR-Harris空间耗费的时间为3.27 s，关键点搜索的时间为1.45 s，若限制输入后续环节的关键点数目为500以下，则特征向量的生成时间为9.61 s，次近邻筛选时间与RANSAC时间为5.46 s，最终得到的稳定匹配点对为28对，共耗时19.8 s。然而当关键点数目达到5000时，特征向量的生成以及匹配筛选的时间分别长达100.41 s与26.76 s，稳定匹配点对为90对，算法总体耗时为131.9 s。文中进行对比的SAR-SIFT算法所采用的关键点数目为500。

许多学者针对SIFT类算法在CPU上运算时间的劣势，提出了基于GPU或多核DSP的加速算法，能够获得几十的加速比，使得SIFT类算法的实时性得到了很大提升[23]。由此推算，即使在关键点数目较多的情况下，SAR-SIFT并行加速算法的速度也可降低至几秒甚至一秒以内。

本文的算法采用了深度卷积神经网络架构，计算过程具有较高的可并行性，因此在实际部署时若采用GPU则会大幅提高其运算速度。对于1200×1200大小的Wallerfing图像，基于CPU的前向推断的运算时间为27.09 s，而基于GPU的运算时间仅为0.9943 s。因此本文的算法即使在大场景条件下也具备较快的执行速度。此外，由于网络的输出结果为经过滤波后的所有匹配点对的置信度，筛选前N个稳定匹配点对的时间复杂度仅为O(N)，故本文算法增加稳定匹配点对的额外时间开销较小。本文并未针对网络结构进行模型压缩，当前关于深度卷积神经网络在移动端部署的研究也较为丰富，后续可以考虑利用模型蒸馏或参数压缩等方法对网络进行压缩，从而实现网络前向推断速度的加快以及轻量级平台上的部署。

总之，在用于匹配的特征点数适中的情况下，经过并行加速后的SIFT类算法相比于本文算法在理论上具有一定的时间优势，但是本文算法也同样具备较高的实时性以及潜在的算法加速的可能性，且增加匹配点对的额外时间开销较小。

(6) 本文算法的适用条件

本文的算法适用于高分辨率且尺寸适中的图像。极化SAR图像成像分辨率较低时，训练集与测试集的数据分布会具有较大差异性，配准性能可能下降；极化SAR图像尺寸过小(例如500×500以下)时，16倍降采样特征图所包含的特征点过少，配准会失效。后续研究中，可以针对小场景图像，重新设计网络结构，提高输出特征图的分辨率，实现高分辨率下的特征匹配过滤，完成小图像的配准。

本文的算法仅适用于全局仿射配准，不适用于更加精细、配准模型自由度更高的全局极化SAR图像配准。本文的端到端极化SAR图像仿射配准算法利用了稀疏卷积来降低网络参数量，使得输入图像的尺寸可达1000×1000以上，在仿射配准的精度与速度上均与当前被广泛采用的SAR-SIFT算法相近。然而仿射配准模型的全局自由度仅为6，对于极化SAR图像配准任务而言，建模仍较为粗糙。本文算法基于16倍降采样的特征图进行特征稀疏匹配与过滤，映射至高分辨原图的单点位置精度较低，而SAR-SIFT算法则对关键点进行精细插值定位。可以预见，当配准模型较为复杂时，本文方法的精度相比于传统的SAR-SIFT等算法具有一定劣势。随着显卡的更新换代，未来可以尝试通过对网络结构进行改进，实现高分辨率图像下的点对匹配，以完善上述缺陷。

5 结论

针对目前基于深度学习的极化SAR图像配准算法需要对图像进行手动切块处理与参数迭代估计，致使流程较为烦琐的问题，本文提出一种端到端的基于深度卷积神经网络的极化SAR图像仿射配准算法。该算法将特征提取与特征匹配过滤模块整合在同一神经网络框架中，基于弱监督学习实现了基于邻域一致性的特征精细匹配。结合网络输出结果与带权最小二乘法即可实现仿射变换参数的一步求解，无需参数的迭代估计，流程简洁。实验结果表明，该算法能够有效地利用多通道的极化信息提取稳定的特征匹配点对；算法采用DenseNet作为特征提取结构，整体配准精度与传统算法相近，在1200×1200的分辨率下，配准后的平均像素误差距离低至2.5～6.2，全局平均像素误差距离与边长之比低至0.2%～0.5%；速度上，本文的算法能够满足海量数据的实际应用需求。此外，实验利用了升轨和降轨、不同成像模式、不同极化方式、不同分辨率的SAR数据进行验证，结果表明本文提出的方法在不同数据上具有良好的泛化性能。