有中介的调节模型的拓展及其效应量*

刘红云 袁克海 甘凯宇

有中介的调节模型的拓展及其效应量

刘红云袁克海甘凯宇

(北京师范大学心理学部;北京师范大学心理学部应用实验心理北京市重点实验室, 北京 100875) (南京邮电大学理学院, 南京 210023) (美国圣母大学心理系, 印第安纳州 46556, 美国)

传统的有中介的调节(mediated moderation, meMO)模型关于误差方差齐性的假设经常被违背, 应用研究中也缺乏测量meMO效应大小的指标。对于单层数据, 本文借助于两层建模的思想, 提出了一种可用于处理方差非齐性的两层有中介的调节(2meMO)模型; 给出了用于测量meMO分析中总调节效应、直接调节效应和有中介调节效应大小的效应量。通过Monte Carlo模拟研究, 比较了meMO和2meMO模型在参数和效应量估计上的表现。并通过实际案例解释了2meMO模型的应用以及效应量的计算和解释。

有中介的调节, 方差齐性, 效应量, 贝叶斯估计

1 引言

在很多领域的实际研究中, 中介(mediation)效应分析和调节(moderation)效应分析是探讨自变量和因变量之间复杂关系常用的两类方法。随着研究问题的深入, 在更系统的理论框架下, 将中介效应与调节效应结合, 探讨变量之间更为复杂关系的研究方法越来越受到重视( Kwan & Chan, 2018; 叶宝娟, 温忠麟, 2013)。其中, 有中介的调节(mediated moderation, 简称meMO)模型在探讨调节变量作用机制方面, 提供了强有力的分析方法。

meMO模型分析的重点是探讨调节变量对自变量()与因变量()之间关系的作用机制, 如果对和之间关系的调节通过中介的调节变量()(mediating moderator)起作用, 则称通过对和之间关系间接的调节为有中介的调节(meMO)。基于不同理论的假设, meMO模型近年来在心理学研究中得到了广泛的应用(如, Baron & Kenny, 1986; Liu et al., 2012; Muller et al., 2005; 王玲晓等, 2019; 杨文圣等, 2019; 杨逸群等, 2020)。在方法研究领域, 也有许多研究者就meMO模型的分析步骤和检验方法进行了较为详尽的介绍和总结(Hayes, 2018; Kwan & Chan, 2018; Ng et al., 2019; 叶宝娟, 温忠麟, 2013)。然而, 在实际应用中meMO模型仍至少面临以下三个方面的问题。

首先, 对于meMO模型, 由于缺乏合理的meMO效应量的指标, 应用研究中很少报告其效应量, 或者研究中所选用的替代性指标与meMO研究感兴趣的问题不匹配。针对研究报告中过分强调统计显著性的问题, 越来越多的期刊要求研究者提供效应量和区间估计的结果(如, American Education Research Association, 2006; Cumming, 2014; Funder et al., 2013; Rozeboom, 1960; Wilkinson & American Psychological Association Task Force on Statistical Inference, 1999), 国内的《心理学报》和《心理科学》等杂志也有同样的要求。然而, 到目前为止, 研究者没有结合meMO问题的特点对其效应量进行针对性的测量和解释。有研究者借鉴其他类似的效应量作为替代品, 如采用回归分析中常用的描述增加了有中介的调节路径后, 因变量变异解释率的增加(Aiken et al., 1991), 但这些指标并不合适。因为从效应量定义的本质来看, 效应量是反应某种现象(如影响程度)大小的数量化表示, 合适的效应量应直接针对所感兴趣的研究问题(Kelley & Preacher, 2012)。因此, 亟待解决的问题是如何围绕meMO分析感兴趣的“通过调节和之间的关系”问题, 构建合理的效应量指标, 对meMO分析中关注的有中介的调节效应大小进行评价。

其次, 有中介的调节(meMO)和有调节的中介(moderated mediation, 简称moME)虽然解释的侧重点不同, 但是在实际应用中经常被研究者混淆。Baron和Kenny (1986)最早提出了meMO和moME的概念, 很多研究随后就这两类分析进行了详细的阐述(Edwards & Lambert, 2007; Liu et al., 2012; Muller et al., 2005)。Hayes (2018)结合概念模型和统计模型, 对meMO和moME进行了详细的分类, 并提供了PROCESS分析程序。然而, 对于应用研究者来讲清晰区分两类模型并不容易, 研究中经常会出现理论假设中变量之间的关系是moME(或meMO)的叙述, 而在统计模型结果的解释上却采用了meMO(或moME)的解释(如, Gonzalez-Mulé et al., 2016; Liang & Chi, 2013; Park & Searcy, 2012; Tang, 2016; Tang & Naumann, 2016; Zacher et al., 2012; 杨文圣等, 2019)。究其根本原因是因为在数据分析上, meMO与moME对应的统计模型相同, 导致研究者对meMO和moME产生了混淆。具体来讲, 常用的meMO模型分为meMO-I型和meMO-II型两类, meMO-I模型与第一阶段moME模型等价, meMO-II模型与第二阶段moME模型等价(Kwan & Chan, 2018)。本文关注的问题是如何从概念模型出发, 在统计模型的表述上突出meMO模型关注的变量间关系以及调节变量的作用机制, 定义合理的效应量, 以在结果解释上区分meMO和moME两类模型。

最后, meMO模型假设误差方差齐性, 回归系数显著性的检验也基于这一假设, 然而实际应用中这一假设常常不成立, 尤其是包含调节效应的模型(Aguinis & Pierce, 1998; DeShon & Alexander, 1996)。例如, 对于含有交互作用的回归模型

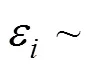
为了处理调节效应分析容易导致的方差非齐性的问题, Yuan等人(2014)采用两层模型扩展了传统的调节效应回归模型, 并据此定义了测量调节效应大小的指标。虽然Yuan等人(2014)没有涉及meMO模型, 但他们提出的两层建模的思想和效应量定义的出发点对调节效应拓展到更复杂的模型是有启发的。本研究将借鉴两层模型定义的思路, 将其拓展到复杂的有中介的调节模型的情景, 并基于此定义既适用于方差齐性条件, 又适用于方差非齐性条件的meMO效应量指标。

综上, 本研究主要解决以下问题：首先从有中介的调节的概念模型出发, 将Yuan等人(2014)定义的两层调节回归模型拓展到两层有中介的调节(2meMO)模型; 其次通过对自变量与因变量之间关系变异来源的分解, 给出测量meMO效应量大小的指标; 然后通过模拟研究评估模型参数以及效应量估计的精度, 并通过与传统meMO比较, 验证拓展模型的合理性; 同时采用实际数据案例和Mplus (Muthén & Muthén, 2017)语句介绍2meMO模型的应用以及效应量的估计和解释, 以方便应用者使用; 最后指出方法的可拓展性以及效应量指标的优缺点和实际应用中应注意的问题。

2 有中介的调节模型的拓展

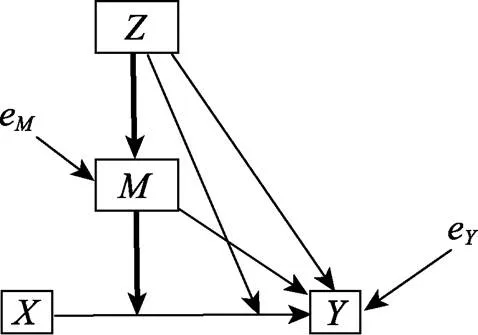
图1 有中介的调节效应的概念模型(粗体线表示有中介的调节效应)

层1:

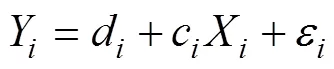
层2:

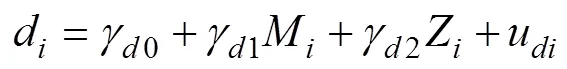
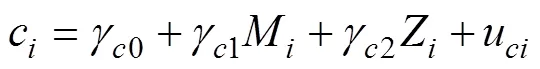
图2 拓展的有中介的调节(2meMO)分析对应的分层统计模型(粗体线表示有中介的调节路径)

下面通过合并模型的表达进一步明确2meMO模型和传统meMO模型的联系和区别。将(3)和(4)代入到(2)中, 得到合并模型的表达式为：

再将等式(5)代入到等式(6)中, 得到：

图3 拓展的有中介的调节(2meMO)分析对应的合并统计模型(粗体线表示有中介的调节路径)

3 meMO效应量的定义

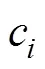
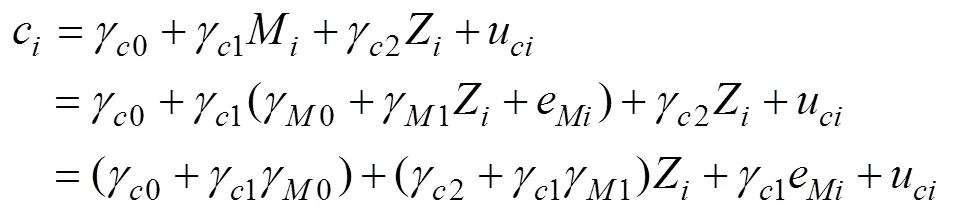
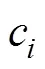
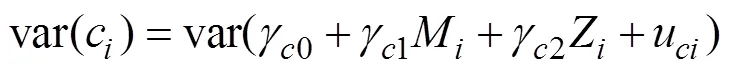
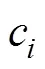
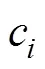
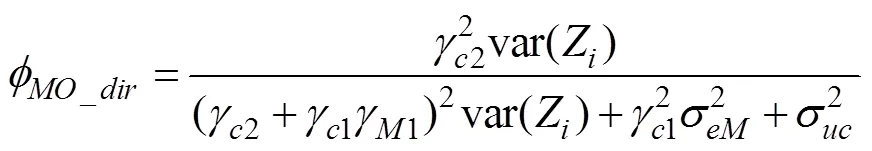
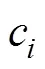
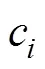
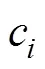
总调节效应：

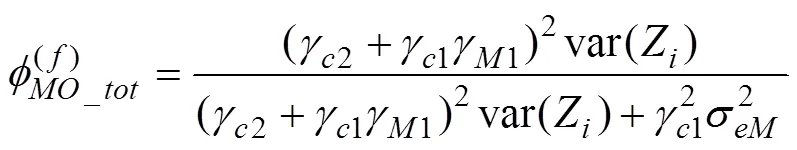
直接的调节效应：

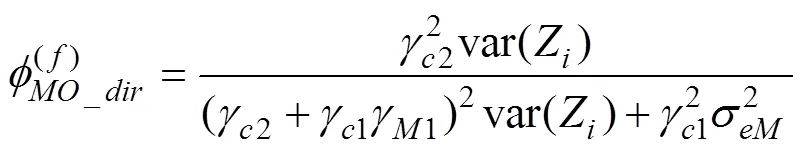
中介的调节效应：

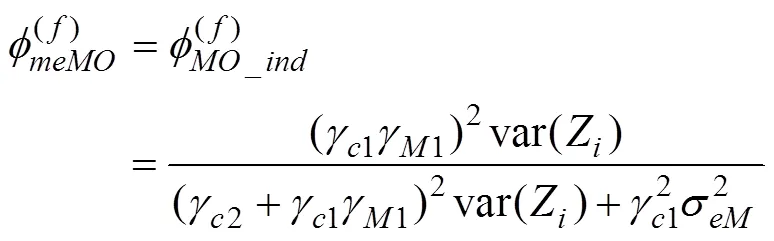
这里, 我们使用上标()来区分定义中不包含的对未解释的随机残差。

由于本研究拓展的2meMO模型随机部分参数更复杂, 极大似然估计方法会遇到基本假设(误差方差齐性)被违背的问题。考虑到贝叶斯估计在处理复杂模型, 尤其是含有更复杂的随机变异模型时更加灵活的优势(Wang Preacher, 2015; Muthén & Asparouhov, 2012; Asparouhov & Muthén, 2020), 我们使用贝叶斯方法估计2meMO中的参数及效应量。为了便于比较, 贝叶斯估计方法也用于meMO模型的参数估计。在指定模型和先验分布后, 采用马尔可夫链蒙特卡洛(Markov Chain Monte Carlo, MCMC) Gibbs采样获得模型参数的后验分布(Gilks et al., 1996)。关于Gibbs采样收敛性的检查, 使用Gelman-Rubin势能缩减(potential scale reduction, PSR)统计量。根据Brooks和Gelman (1998)的研究, 如果PSR统计量小于1.05, 则认为参数估计达到收敛。对于收敛样本, 我们将参数的贝叶斯估计定义为其后验分布的均值(称为后验均值, 实际中也可用中位数), 并且使用收敛样本的标准差获得后验标准差。基于每个参数后验分布2.5%和97.5%的分位数, 得到95%可信区间(Credibility Interval, CI)(Song & Lee, 2012)。

4 模拟研究

本研究通过模拟研究的方法, 比较不同条件下, meMO和2meMO在参数估计精度和效应量估计方面的表现。通过meMO和2meMO的比较, 验证方差齐性条件不满足时, 拓展的2meMO模型的必要性。

4.1 模拟设计

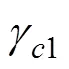
4.2 数据分析和评价指标

偏差(Bias)和均方误差(MSE)的定义如下：

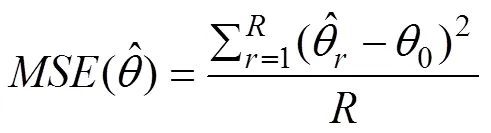
95%可信区间的覆盖率是指500次重复中贝叶斯估计得到的后验分布中第2.5%和第97.5%可信区间内包含参数真值的次数所占的比例。检验力是在参数对应的真值不为0的条件下,500次重复中能够检验出参数显著不为零的次数所占的比例。第一类错误是在参数对应的真值为0的条件下,500次重复中错误的检验出参数显著不为0的次数所占的比例。

4.3 结果

对于每一组模拟条件, 模型中所有参数对应的PSR统计量均小于1.05, 说明对于meMO和2meMO模型, 贝叶斯估计均不存在不收敛的问题。

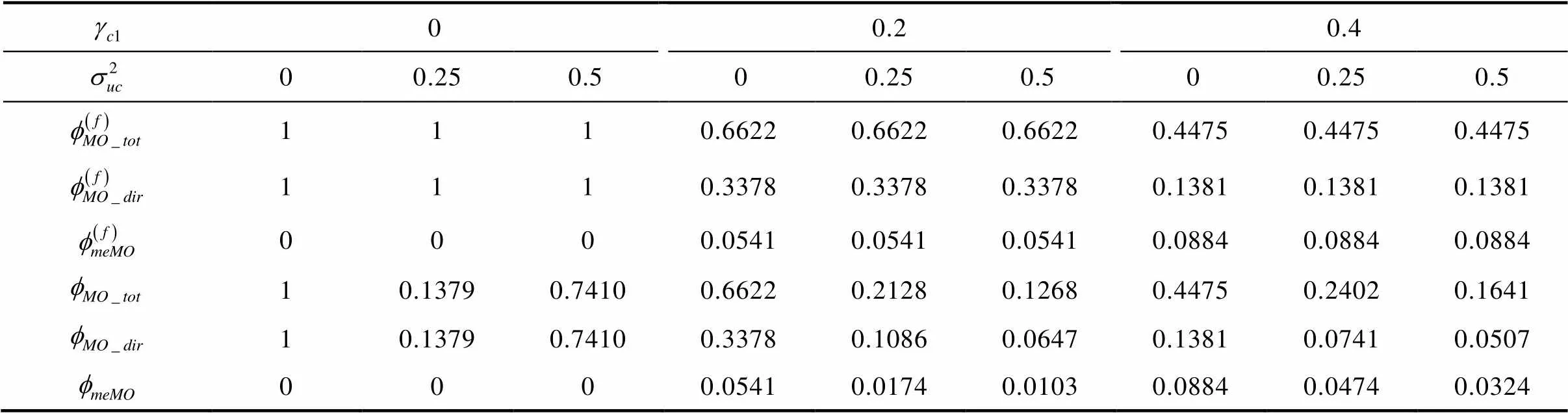
表1 模拟设计条件对应的效应量真值

表2 两种模型得到的的偏差, 均方误差, 95%可信区间覆盖率和拒绝率

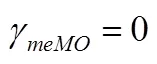
4.3.2 效应量的估计结果

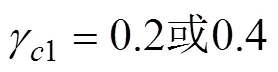
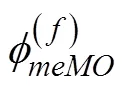
5 应用案例

5.1 数据和模型

为了便于2meMO模型与meMO模型的比较, 这里我们采用Kwan和Chan (2018)研究中所用的数据(下载地址：http://dx.doi.org/10.1037/met0000160. supp)。其数据来源于2012年OECD (Organization for Economic Cooperation and Development)组织的PISA测试(the Program for International Student Assessment, PISA), 具体介绍见Kwan和Chan (2018)研究中的介绍。该数据样本量为3047, 分析的变量包括：因变量数学学业成绩(MATH), 自变量数学自我效能(MEFF), 调节变量社会经济地位(ESCS)以及中介的调节变量家庭教育资源(HRES)。模型假设：ESCS可以调节MEFF与MATH之间的关系, ESCS较低的学生, MEFF对MATH的影响较强, 而ESCS较高的学生, MEFF对MATH的影响较弱; 进一步, ESCS对MEFF与MATH之间关系的调节作用被HRES所中介, ESCS高的学生拥有较多的HRES, 所以MEFF对MATH的影响较弱。对应的概念模型见图4, 分析的模型包括传统meMO模型和2meMO模型, 分析过程中对MEFF、ESCS和HRES做均值中心化处理。为了帮助应用者理解和便于应用者使用分析程序, 我们在网络版附录中给出了默认先验设置时Mplus 8.3的语句。需要再次强调的是这里的数据是单层次结构, 在Mplus中我们借助于多层模型采用贝叶斯估计方法实现2meMO的参数估计, 一个个体就是一个cluster。

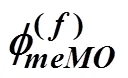
表3 两种模型得到的效应量估计的偏差, 均方误差, 95%可信区间覆盖率

注：覆盖率低于0.9的值用粗体字表示。

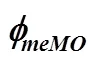
表4 2meMO模型得到的效应量估计的偏差, 均方误差, 95%可信区间覆盖率

注：对于2meMO模型, 由于方差估计大于0, 置信区间的覆盖率均不包含0。

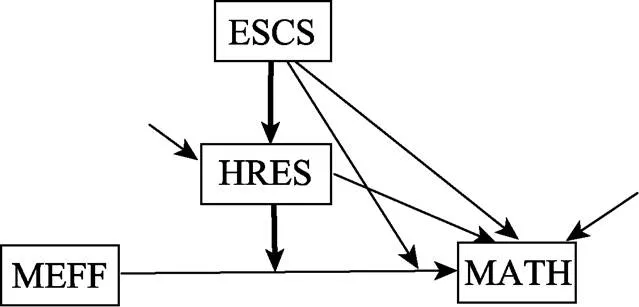
图4 家庭教育资源对社会经济地位与数学自我效能与数学成绩之间中介调节效应模型(粗体线表示有中介的调节效应)

5.2 分析结果

对于meMO模型和2meMO模型, 在默认先验设置条件下模型中所有参数对应的PSR统计量均介于1.00到1.02之间, 进一步检查3条不同链的轨迹图发现不同链条收敛到同样的后验分布。表6给出了两个模型的参数估计结果、中介的调节效应估计值和本研究提出的效应量指标。2meMO模型对应的DIC (Deviance Information Criteria)为78000.4, meMO模型对应的DIC为78069.2, 两个模型对应的DIC的差异ΔDIC = 68.8, 2meMO模型的DIC较小, 根据Cain和Zhang (2019)所建议的ΔDIC > 7的模型比较标准, 2meMO模型的拟合优于meMO模型。

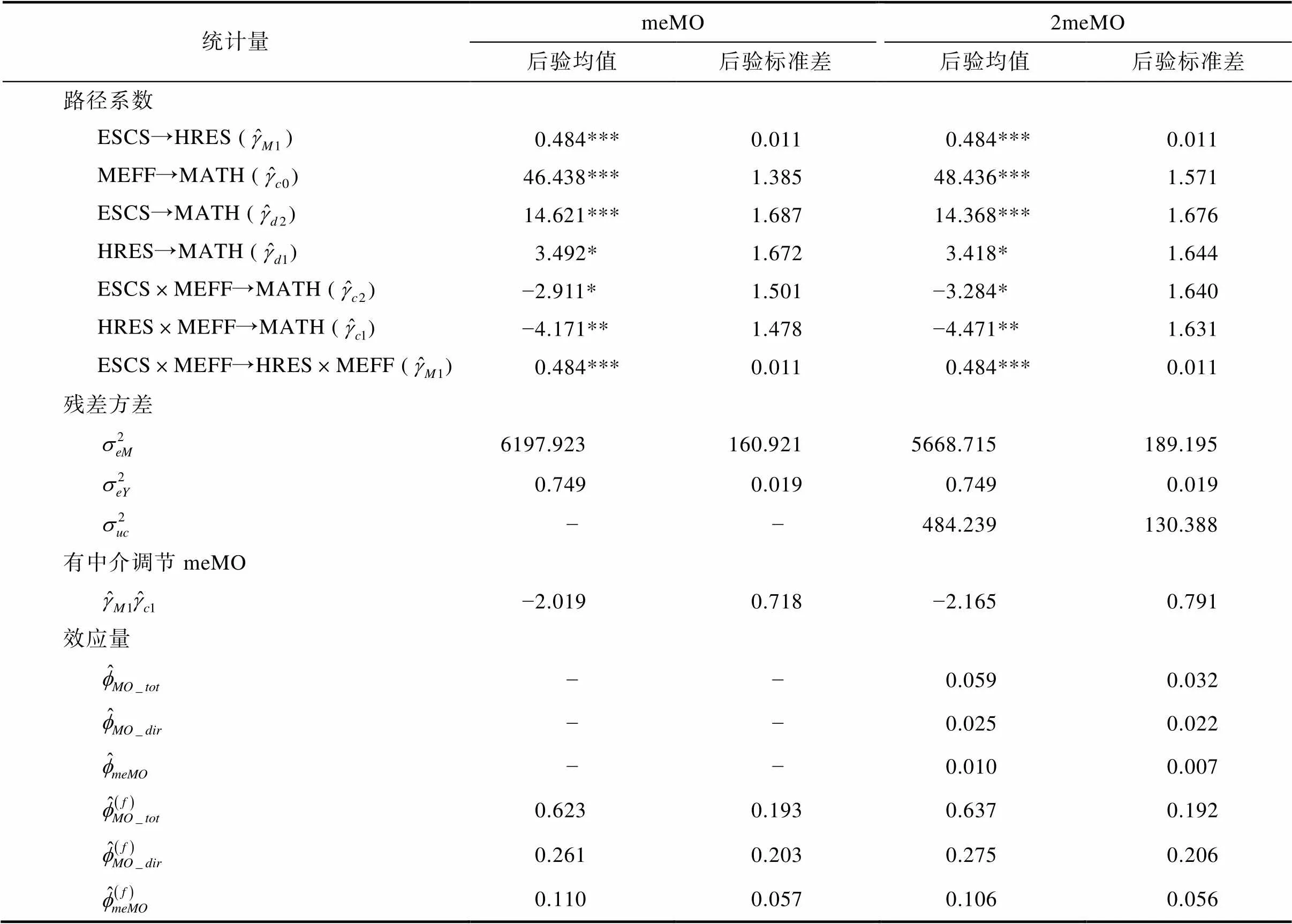
表5 meMO和2meMO模型参数估计结果

6 讨论与建议

本文基于单层的数据拓展了meMO模型, 采用两层模型的框架定义了可处理误差方差非齐性的2meMO模型, 基于此模型将对影响系数变异的来源进行分解, 并由此定义了可以测量总调节效应、直接调节效应和有中介的调节效应大小的效应量指标。进一步将贝叶斯方法用于2meMO模型的参数估计, 并通过Monte Carlo模拟研究考查了参数估计的精度, 并与传统的meMO模型进行了比较, 验证了2meMO模型在处理方差非齐性条件下的优势。

根据模拟研究的结果, 在方差满足齐性的假设时, meMO和2meMO得到的结果几乎没有差异, 也就是说即便在传统meMO的假设下, 2meMO也能得到无偏的精度较高的估计结果。但是在方差齐性的条件不满足时, 2meMO得到的参数估计结果在95%可信区间覆盖率和控制第一类错误上的表现优于meMO模型, 这一结果与方差非齐性的潜变量交互作用模型(Liu et al., 2020)和观测变量的调节效应回归分析模型得到的结果一致(Yang & Yuan, 2016)。2meMO模型的拓展为调节效应模型中常见的方差齐性假设条件的违背(Aguinis & Pierce, 1998; Alexander & DeShon, 1994)提供了解决思路。基于贝叶斯估计方法的可实现性以及模拟研究的结果, 我们推荐研究者使用2meMO模型处理方差非齐性的情况, 在研究中报告与感兴趣的研究问题相对应的效应量指标。

在有中介的调节效应的分析中, 本文提出的2meMO模型和对应的效应量指标有以下几方面的优点：(1)采用两层模型定义meMO统计模型的方式, 在概念模型的理解和效应量的定义上为如何区分变量的角色提供了更为一般化的框架。可以将模型关注的自变量和因变量关系的变化, 定义为层1的模型, 然后根据调节变量的定义, 在层2模型中解释调节变量对因变量和自变量之间关系的影响, 以及调节变量和中介的调节变量之间的关系。这样分层次的模型表达, 合理且有效地区分了自变量、因变量、调节变量和中介的调节变量的不同角色。(2)文中提出的效应量指标是基于自变量和因变量之间总变异(即var(c))的分解所得到的, 这就为紧密围绕“与之间关系的调节”这一关键问题, 定义合适的效应量提供了基础, 基于此所定义的效应量是围绕meMO分析所感兴趣的问题提出的, 更具可解释性, 同时也更符合效应量概念的核心内涵(e.g., Kelley & Preacher, 2012)。(3)基于2meMO提出的效应量指标, 不仅适用于方差齐性而且适用于方差非齐性的条件, 有更广的适用范围。研究者在使用过程中不用担心由于实际数据不满足方差齐性而带来的估计偏差, 检验力降低等问题。(4)2meMO模型的参数估计很容易在Gibbs取样的框架下, 借用已有的免费贝叶斯估计程序实现。如2meMO的参数估计很容易通过常用的JAGS (Plummer, 2015)、WinBugs (Lunn et al., 2012)和Mplus等软件实现。(5)更重要的是, 本文所提出的有中介的调节模型的效应量指标可满足应用研究者报告效应量的需求, 弥补了目前尚没有合适的测量meMO影响的效应量指标的局限。

另外, 本研究定义模型的方法和效应量的思路具有拓展性。本文提出的定义2meMO模型的思路, 可以在概念上为如何有效区分meMO和moME两类模型提供一些借鉴。从概念模型来看, 2meMO模型和moME-II强调的重点不同, 两者并不等价, 2meMO模型是为了解释调节效应是如何通过中介的调节变量发挥作用的; 而moME-II是为了解释中介效应是如何依赖于调节变量取值的。然而, 传统的方差齐性假设下由于两者对应的统计模型相同, 在结果解释上很难有效帮助应用研究者区分两类模型的本质区别。在两层建模的框架下, 对于moME模型可以借鉴本文的建模思路, 在层1定义与中介效应有关的路径(和), 而在层2解释中介路径中某个阶段的效应被调节。例如, 含有第二阶段被调节的中介模型可以定义为：

层1:

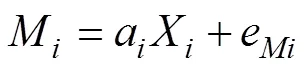
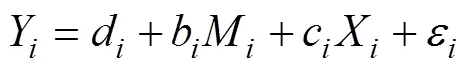
层2:

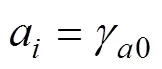
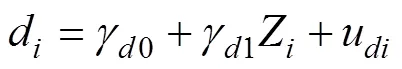
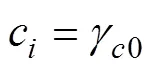
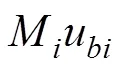
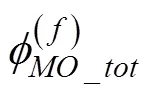
虽然所提出来的效应量具有很多优点, 但在应用时也应关注其局限性。首先, 类似于方差分析中的偏η, var(c)是定义效应量的基础(分母), 即效应量的解释都是以var(c)作为比较基准的, 因此这些效应量本质上是一个相对的效应量指标。因此, 在实际应用中, 在报告效应量的时候应同时报告分母的大小, 以避免过度夸大meMO效应, 同时也有助于了解在对的影响中, var(c)的大小是否有实际的意义。研究者应该在关注var(c)本身大小的前提下, 进一步解释meMO效应的大小。另外, 我们建议在报告效应量的时候, 同时报告本研究提出的多个效应量指标, 为全面了解变量的影响关系和强度提供更多的补充信息。同时, 应该注意基于变异分解所定义的直接调节效应和间接调解效应的效应量指标不具有可加性。

大量的研究证明不同先验分布会影响参数估计的精度(Yuan & MacKinnon, 2009), 因此, 实际中如何选择合适的先验分布是研究者应该注意的问题。本研究选取了最常用也是研究者广泛推荐的无信息先验(Browne & Draper, 2006), 结果证明即使是无信息的先验也能够得到准确的参数估计结果, 但是这一结论在实际应用中并不一定具有普适性。已有研究表明合适的有信息先验可以使得参数估计精度更高, Zondervan-Zwijnenburg等人(2017)提供了如何收集先验信息的指导。如果研究者可以得到合适的有信息的先验, 我们也鼓励采用有信息的先验以提高参数估计的精度。然而, 为了避免由于特定先验设置带来的主观性, 应当考虑采用敏感性分析进一步确认贝叶斯估计结果并不严重依赖于某个特定的先验分布(van de Schoot et al., 2017; Zondervan-Zwijnenburg et al., 2017)。

本研究只考虑了含有一个调节变量和一个中介的调节变量的情况, 对于方差非齐性也只考虑了结果变量的方差非齐性, 未来研究中可以考虑更为复杂的meMO模型和更复杂的方差非齐性的情况。另外, 对于本研究提出的效应量指标, 如何结合效应量的特点, 给出效应量“小”、“中”、“大”的判断标准, 也是未来值得进一步研究的问题。最后, 模型中被忽略的变量、变量的测量误差和其他影响回归系数估计精度的因素也会对效应量的估计精度产生影响, 未来研究需要对这些影响因素进行更为系统和深入的探讨。

Aguinis, H., & Pierce, C. A. (1998). Heterogeneity of error variance and the assessment of moderating effects of categorical variables: A conceptual review.(3), 296–314.

Aiken, L. S., West, S. G., & Reno, R. R. (1991).London, UK: SAGE Publications.

Alexander, R. A., & DeShon, R. P. (1994). Effect of error variance heterogeneity on the power of tests for regression slope differences.(2),308–314.

American Education Research Association. (2006). Standards for reporting on empirical social science research in AERA publications.(6),33–40.

Asparouhov, T., & Muthén, B. (2020). Bayesian estimation of single and multilevel models with latent variable interactions., 1–15.

Baron, R. M., & Kenny, D. A. (1986). The moderator– mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations.(6), 1173–1182.

Brooks, S. P., & Gelman, A. (1998). General methods for monitoring convergence of iterative simulations.(4), 434–455.

Browne, W. J., & Draper, D. (2006). A comparison of Bayesian and likelihood-based methods for fitting multilevel models., 473–514.

Cain, M. K., & Zhang, Z. Y. (2019). Fit for a Bayesian: An evaluation of PPP and DIC for structural equation modeling.(1), 39–50.

Cumming, G. (2014). The new statistics: Why and how.(1), 7–29.

DeShon, R. P., & Alexander, R. A. (1996). Alternative procedures for testing regression slope homogeneity when group error variances are unequal.(3), 261.

Edwards, J. R., & Lambert, L. S. (2007). Methods for integrating moderation and mediation: A general analytical framework using moderated path analysis.(1), 1–22.

Funder, D., Levine, J., Mackie, D., Morf, C., Sansone, C., West, S., & Vazire, S. (2013).. Retrieved from http://www.spsp.org

Gelman, A., Carlin, J. B., Stern, H. S., & Rubin, D. B. (2004).(2nd ed.). Boca Raton, FL, USA: Chapman & Hall/CRC.

Gilks, W. R., Richardson, S., & Spiegelhalter, D. J. (1996). Introducing Markov chain Monte Carlo. In Gilks, W. R., Richardson, S., & Spiegelhalter, D. J. (Eds.),(pp. 1–20). London, UK: Chapman & Hall.

Gonzalez-Mulé, E., Courtright, S. H., DeGeest, D., Seong, J. -Y., & Hong, D. -S. (2016). Channeled autonomy: The joint effects of autonomy and feedback on team performance through organizational goal clarity., 2018 –2033.

Grant, A. M., & Berry, J. W. (2011). The necessity of others is the mother of invention: Intrinsic and prosocial motivations, perspective taking, and creativity.(1), 73–96.

Hayes, A. F. (2018). Partial, conditional, and moderated mediation: Quantification, inference, and interpretation.(1), 4–40.

Hayes, A. F., & Preacher, K. J. (2013). Conditional process modeling: Using structural equation modeling to examine contingent causal processes. In G. R. Hancock & R. O. Mueller (Eds.), Quantitative methods in education and the behavioral sciences: Issues, research, and teaching. Structural equation modeling: A second course (pp. 219–266). IAP Information Age Publishing.

Kelley, K., & Preacher, K. J. (2012). On effect size.(2), 137–152.

Kwan, J. L. Y., & Chan, W. Y. (2018). Variable system: An alternative approach for the analysis of mediated moderation.(2), 262–277.

Lachowicz, M. J., Preacher, K. J., & Kelley, K. (2018). A novel measure of effect size for mediation analysis.(2), 244–261.

Liang, S. G., & Chi, S. C. S. (2013). Transformational leadership and follower task performance: The role of susceptibility to positive emotions and follower positive emotions., 17–29.

Liu, D., Zhang, Z., & Wang, M. (2012). Mono-level and multilevel mediated moderation and moderated mediation: Theorizing and test. In X. Chen, A. Tsui, & L. Farh (Eds.),[in Chinese] (2nd ed., pp. 545–579). Beijing, China: Peking University Press.

Liu., H. Y., Yuan, K -H., & Liu, F. (2020). A two-level moderated latent variable model with single-level data,(6), 873–893.https://doi.org/10.1080/00273171.2019.1689350

Lunn, D., Jackson, C., Best, N., Spiegelhalter, D., & Thomas, A. (2012).. Boca Raton, FL, USA: Chapman and Hall/CRC.

Lutz, J. G. (1983). A method for constructing data which illustrate three types of suppressor variables., 373–377.

Maassen, G. H., & Bakker, A. B. (2001). Suppressor variables in path models: Definitions and interpretations.,, 241–270.

Muller, D., Judd, C. M., & Yzerbyt, V. Y. (2005). When moderation is mediated and mediation is moderated.(6), 852– 863.

Muthén, B., & Asparouhov, T. (2012). Bayesian structural equation modeling: A more flexible representation of substantive theory.(3), 313–335.

Muthén, L. K., & Muthén, B. O. (2017).(Version 8). Los Angeles, CA: Authors.

Ng, J. C. K., Chan, W., Kwan, J. L. Y., & Chen, X. H. (2019). Unpacking structure-oriented cultural differences through a mediated moderation model: A tutorial with an empirical illustration.(3), 358–380.

Park, R., & Searcy, D. (2012). Job autonomy as a predictor of mental well-being: The moderating role of quality- competitive environment.,305–316.

Plummer, M. (2015).Retrieved from http://www.uvm.edu/~bbeckage/Teaching/ PBIO_294/Manuals/manual.jags.pdf

Preacher, K. J., & Kelley, K. (2011). Effect size measures for mediation models: Quantitative strategies for communicating indirect effects. Psychological Methods, 16(2), 93–115.http://dx.doi.org/10.1037/a0022658

R Core Team. (2016). R: A language and environment for statistical computing.. Retrieved from https://www.r- project.org/

Rozeboom, W. W. (1960). The fallacy of the null-hypothesis significance test.(5), 416–428.

Song, X. -Y., & Lee, S. -Y. (2012). A tutorial on the Bayesian approach for analyzing structural equation models.(3), 135–148.

Tang, C. Y. (2016). Accessed external knowledge, centrality of intra-team knowledge networks, and R&D employee creativity.(Suppl. 3), 992–1005.

Tang, C. Y., & Naumann, S. E. (2016). Team diversity, mood, and team creativity: The role of team knowledge sharing in Chinese R&D teams., 420–434.

Tzelgov, J., & Henik, A. (1991). Suppression situations in psychological research: Definitions, implications, and applications., 524–536.

van de Schoot, R., Winter, S. D., Ryan, O., Zondervan- Zwijnenburg, M., & Depaoli, S. (2017). A systematic review of Bayesian papers in psychology: The last 25 years.(2), 217–239.

Wang, L. J., & Preacher, K. J. (2015). Moderated mediation analysis using Bayesian methods.(2), 249–263.

Wang, L. X., Zhang, L. Y., & Chang, S. M. (2019). The relationship between maternal rejection and peer rejection: A mediated moderation model.(6), 1347–1353.

[王玲晓, 张丽娅, 常淑敏. (2019). 儿童母亲拒绝与同伴拒绝的关系— 一个有中介的调节模型.(6), 1347–1353.]

Wen, Z. L., & Fan, X. T. (2015). Monotonicity of effect sizes: Questioning kappa-squared as mediation effect size measure.(2), 193–203.

Wen, Z. L., Marsh, H. W., & Hau, K. -T. (2010). Structural equation models of latent interactions: An appropriate standardized solution and its scale-free properties.(1), 1–22.

Wilkinson, L. Task Force on Statistical Inference, American Psychological Association, Science Directorate. (1999). Statistical methods in psychology journals: Guidelines and explanations. American Psychologist, 54(8), 594–604.

Yang, W. S., Mu, J. Z., Li, B. W., & Wang, J. Y. (2019). Relationship between proactive personality and employee behaviors: The role of proactive socialization behavior and political skill.(6), 1488–1454.

[杨文圣, 牟家增, 李博文, 王佳颖. (2019). 主动性人格与员工行为的关系：政治技能视角下有中介的调节模型.(6), 1488–1454.]

Yang, M., & Yuan, K. -H. (2016). Robust methods for moderation analysis with a two-level regression model.(6), 757–771.

Yang, Y. C., Chen, L., Chen, G. H., & Zhang, W. X. (2020). Peer rejection, friendship support and adolescent depressive symptoms: A mediated moderation model.(2), 348–353.

[杨逸群, 陈亮, 陈光辉, 张文新. (2020). 同伴拒绝、友谊支持对青少年抑郁的影响：有中介的调节模型.(2), 348–353.]

Ye, B. J., & Wen, Z. L. (2013). A discussion on testing tethods for mediated moderation models: Discrimination and integration.(9), 1050–1060.

[叶宝娟, 温忠麟. (2013). 有中介的调节模型检验方法：甄别和整合.(9), 1050–1060.]

Yuan, K. -H., Cheng, Y., & Maxwell, S. (2014). Moderation analysis using a two-level regression model.(4), 701–732.

Yuan, Y., & MacKinnon, D. P. (2009). Bayesian mediation analysis.(4), 301–322.

Zacher, H., Jimmieson, N. L., & Winter, G. (2012). Eldercare demands, mental health, and work performance: The moderating role of satisfaction with eldercare tasks., 52–64.

Zondervan-Zwijnenburg, M., Peeters, M., Depaoli, S., & van de Schoot, R. (2017). Where do priors come from? Applying guidelines to construct informative priors in small sample research.(4), 305–320.

Two-level mediated moderation models with single level data and new measures of effect sizes

LIU Hongyun, YUAN Ke-Hai, GAN Kaiyu

(Faculty of Psychology, Beijing Normal University, Beijing 100875, China) (Beijing Key Laboratory of Applied Experimental Psychology, Faculty of Psychology, Beijing Normal University, Beijing 100875, China) (School of Science of Nanjing University of Posts and Telecommunications, Nanjing, 210023, China) (Department of Psychology, University of Notre Dame, IN 46556, USA)

Mediation and moderation analyses are commonly used methods for studying the relationship between an independent variable () and a dependent variable () in conducting empirical research. To better understand the relationships among variables, there is an increasing demand for a more general theoretical framework that combines moderation and mediation analyses. Recently, statistical analysis of mediated moderation (meMO) effects has become a powerful tool for scientists to investigate complex processes. However, the traditional meMO model is formulated based on the homoscedasticity assumption, which is most likely to be violated when moderation effects exist. In addition, routinely reporting effect sizes has been recommended as the primary solution to the issue of overemphasis on significance testing. Appropriate effect sizes (ES) for measuring meMO effects are very important in reporting and interpreting inferential results. However, there does not exist an effective measure that allows us to answer the question regarding the extent to which a variablemoderates the effect ofonvia the mediator variable () in the meMO model.

The article is organized as follows. First, the two-level moderated regression model proposed by Yuan, Cheng, & Maxwell (2014) was extended to a two-level mediated moderation (2meMO) model with single-level data, the statistical path diagram was structured according to the conceptual model and the equations. Second, several effect sizes were developed for the 2meMO effect by decomposing the total variance of the moderation effect. Third, to estimate the parameters of the 2meMO model and the ES measures of the meMO effects, we developed a Bayesian estimation method to estimate the parameters of the 2meMO model. Fourth, a Monte Carlo simulation study was conducted to evaluate the performance of the 2meMO model and the proposed ES measures against those with the meMO model. Finally, we illustrate the application of the new model and measures with a real data example.

In summary, the article developed a 2meMO model with single-level data and proposed several measures to evaluate the size of the meMO effect explained by moderator variables in total, directly, or indirectly. The performance of the 2meMO model is compared against that of the traditional meMO model via Monte Carlo simulations. Results indicate that, when the assumption of homoscedasticity holds, 2meMO yields comparable results with those under meMO. When the homoscedasticity assumption is violated, estimates under 2meMO are more accurate than those under meMO. More importantly, the measures of the size of the meMO effect proposed in this article can be used as a supplement to the test of meMO effects and will meet the needs for reporting ES in practice. Consequently, the 2meMO model is recommended for the analysis of mediated moderation, and the effect sizes (ESs) for the interpretation of the effect according to the questions of interest are better reported.

mediated moderation, heteroscedasticity, effect size, Bayesian estimation

2020-06-25

* 国家自然科学基金项目(31971029, 32071091)资助。

袁克海, E-mail: kyuan@nd.edu

B841.2