灰狼优化支持向量机的推荐算法

杨本臣，裴欢菲

（辽宁工程技术大学 软件学院，辽宁 葫芦岛 125105）

0 引言

推荐系统是使用户更方便找到自己需要的项目，是提升网站运营效益、增加用户忠诚度、解决网站信息超载问题的最有效方法之一.在推荐系统算法中经常引入一些辅助信息作为输入.目前常见的辅助信息有：社交网络、用户/物品属性、上下文等.通过相关文献分析[1-3]，发现存在较低的准确率和召回率、算法复杂等问题，均需进一步深入研究.面对用户深层偏好捕捉困难，容易忽略一些文本的上下文信息等问题，现有分类算法不仅无法有效解决用户-项目矩阵数据稀疏的多分类问题，且同时面临处理海量数据检测耗时，推荐准确率低的复杂问题.因此，如何提出一个面向海量数据能够解决相应特征值选择、推荐准确率低且检测耗时问题的方法是目前亟待解决的问题.

随着神经网络算法的不断改进，以深度学习为代表的人工智能理论与应用研究，越来越多地被应用到推荐系统中.目前许多数据挖掘方法被成功应用到个性化推荐系统的领域中来，比如BP神经网络、遗传算法及决策树等[4-6].文献[7]～文献[9]已经提出可以利用文档主题生成模型和堆栈去噪自动编码器等方法来提取文本中特征并对其进行推荐.但是，现有模型还不能及时捕获有关评论文本的全面信息.为解决上述问题.FU M S[10]等利用卷积神经网络对评论文本数据中的潜在因子进行特征提取.KIM D[11]等提出将卷积神经网络集成到概率矩阵分解中，进行上下文感知推荐，有效提高了推荐准确率.上述推荐模型在特征提取和结合上下文信息等方面已取得了较好推荐结果，但没有进一步与深度神经网络相结合，而且分类结果也有待进一步优化.目前灰狼算法与支持向量机[12]相结合应用在诸多领域中，但很少被应用到个性化推荐系统中.

提出一种基于灰狼优化支持向量机的推荐算法，此算法是在卷积矩阵分解推荐结果的基础上进行了两轮优化.通过对数据集样本进行多层次特征提取、数据填充重建等操作，可以减少大数据带来的数据矩阵稀疏性和冷启动问题.采用灰狼算法对支持向量机参数不断迭代优化，找出全局最优解，实现支持向量机分类识别.

1 用户项目数据预处理

1.1 矩阵分解推荐模型学习

矩阵分解技术通过降维对特征值进行提取，可以有效解决推荐系统中用户—项目评分数据的稀 疏性问题，实现较大程度提取有效信息，得到包含每个用户对推荐项目偏好信息的项目评分矩阵.该评分矩阵由用户User、项目Item和评分组成.为有效缓解原始评分矩阵的极端稀疏情况，评分矩阵 RM×N通过矩阵分解成两个低维的特征矩阵用户UserM×f和项目Itemf×N.

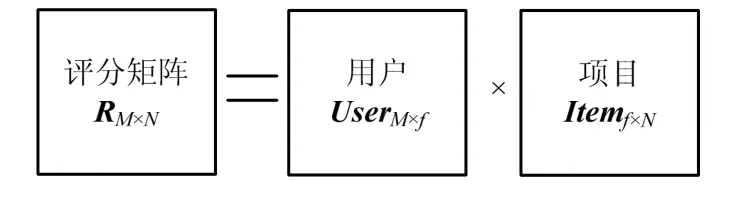
图1 矩阵分解模型示意 Fig.1 model schematic of matrix decomposition

在损失函数中加入正则化参数项ρ及过拟合防止项(||utf||2+||vsf||2)，可以有效避免在优化过程中出现过拟合现象.损失函数为

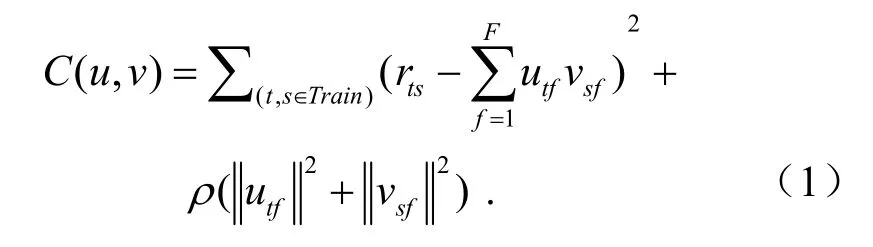
式中，rts为用户t对项目s的评分；utf为用户隐特征向量；vsf为项目的隐特征向量.

使用梯度下降法对上式中的两个参数utf和vsf求偏导数，然后进行迭代优化，确定学习速率α，使其沿较快下降方向梯度下降.通过以上步骤可以实现对矩阵U、V的优化，在训练完成后，可以求得特征矩阵U、V.

1.2 卷积神经网络推荐模型学习

卷积神经网络（CNN）模型是一种基于深度神经网络的多层感知机[13-14]，不适合直接应用于推荐系统中，常被用来特征提取和数据重建，提取项目潜在特征，从而获取项目的低维向量表示.CNN分类模型示意见图2.

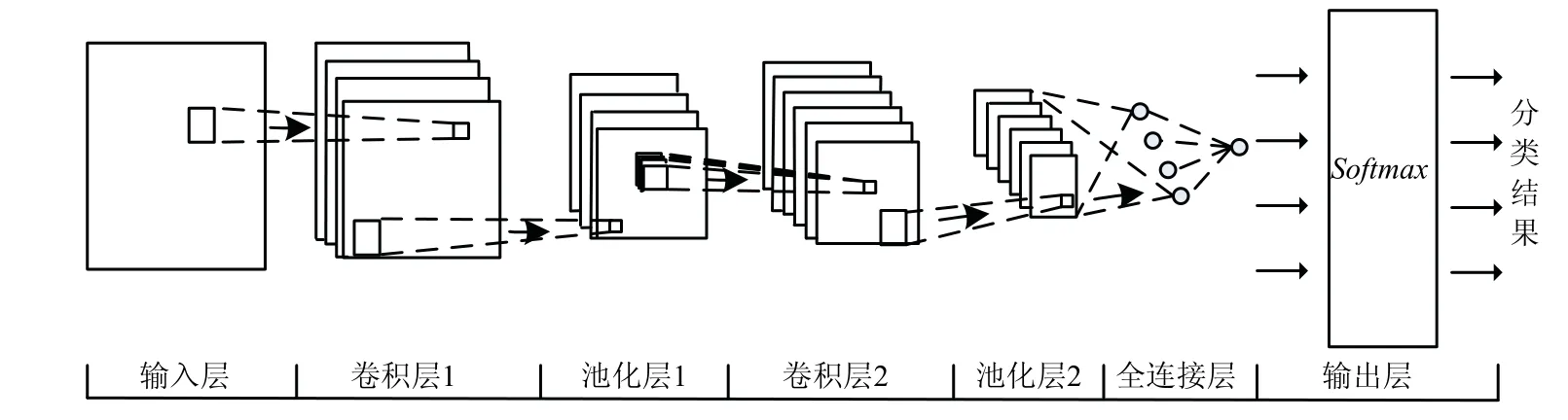
图2 CNN分类模型示意 Fig.2 model schematic of CNN classification

如图2，该模型可以利用卷积层进行卷积操作，代替传统复杂的矩阵乘法运算，与矩阵分解算法结合起来，将两者的优势充分发挥出来构造推荐算法模型.池化层可以有效降低模型中下一层待处理的神经元数量，池化操作可预防过拟合现象发生.另外，CNN拥有权值共享网络结构，减少参数数量，可以有效解决耗时问题，降低算法和网络模型复杂度，进一步提升模型泛化分析能力.

1.3 基于卷积矩阵分解的推荐模型学习

卷积神经网络一般主要解决图像、文本分类问题，而推荐系统是一个回归任务，主要实现在最大限度上准确地预测用户对项目的评分.为了在推荐系统中实现卷积神经网络提取项目的潜在因素，引入卷积矩阵分解（Convolutional Matrix Factoriza- tion）推荐模型，其中的概率矩阵分解，可有效对用户的潜在因素进行提取，比如提取用户社交的历史信息，有效改善冷启动问题.卷积矩阵分解模型[3]见图3.

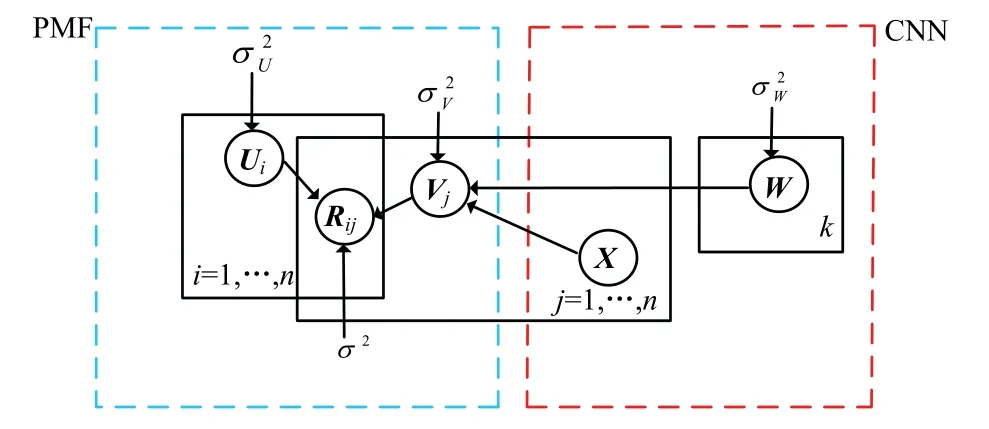
图3 卷积矩阵分解模型示意 Fig.3 model schematic of ConvMF decomposition

如图3，该模型的目标函数由矩阵分解和卷积神经网络损失函数组成[11]，使得即使在用户项目的评分矩阵特别稀疏的情况下，其效果也显著优于其他推荐算法.

2 灰狼算法和支持向量机模型学习

2.1 支持向量机模型

支持向量机（Support Vector Machines，SVM）是Bell实验室的一个研究小组针对小规模样本机器学习方法进行研究[15]时提出来的，是一种可以对未知样本实现最小分类误差的更优分类模式识别方法.支持向量机在解决多维灾难和过拟合等方面也有一定的效果，基于ConvMF模型推荐结果使结果达到更优化，并且还可以克服数据矩阵局部极小点和小样本等问题.

对于线性不可分的特征向量，需采用核函数将向量投放到高维空间中达到可以分类的效果.高斯径向基核函数作为应用最广泛的核函数，在缺乏样本数据的先验知识时，可通过调整参数取得较好的学习效果.高斯径向基核函数为

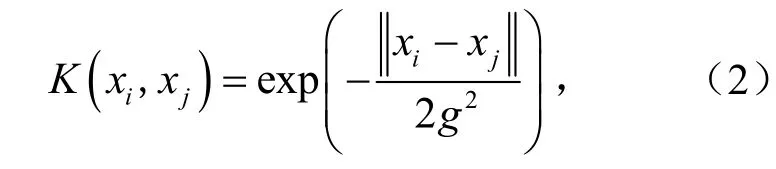
式中，xi、xj为样本集x的两个样本；g为高斯核的带宽，g＞0.

设h维的空间上，针对线性可分问题，所有样本均满足约束条件.约束条件为

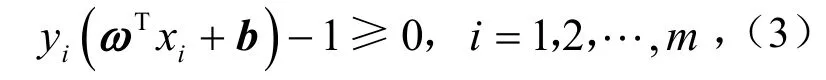
式中，ω为法向量，表示方向；b为分类阈值，表示离超平面的垂直距离；ωTxi+b为分类超平面.

求解支持向量机两类样本最远距离可转化为分类间隔问题.分类间隔为

在实际训练样本数据时，允许出现一些错分的点，通常在约束条件中加入一个大于0的松弛变量，增加一个常数C作为误差惩罚因子后，分类间隔变为

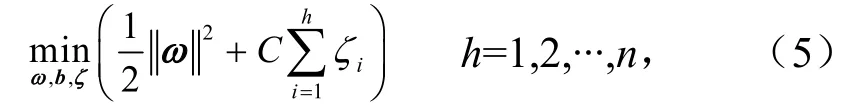
式中，ζ为松驰变量；C为惩罚因子.

以上问题的求解，可以得到SVM回归计算公式为

式中，jα为拉格朗日系数乘积中的因子.

2.2 灰狼优化算法

灰狼优化算法（Wolf Algorithm，GWO）是一种通过模拟灰狼捕猎过程中的狩猎和搜索行为建立的全局随机搜索算法，由MIRJALILI S等在2014年提出的[16].灰狼优化算法与粒子群优化算法（PSO）[17]类似，是一种随机搜索算法，以较大概率收敛于全局最优解，该方法相较于PSO、网格搜索优化算法[18]（GS）等算法，参数少，结构简单，收敛性强，已成功应用在图像处理等领域.

将最优解设为α，第2个和第3个最佳解分别命名为β和δ，而其余的解均设为W.狼群通过3只不同个体狼α、β和δ为初始解，带领狼群W在空间中向它的猎物（最优解）逼近，搜索过程中狼群捕食位置不断迭代更新，引导狼群不断靠近并获得全局最优解.狼群位置更新见图4.

GWO狩猎计算公式为

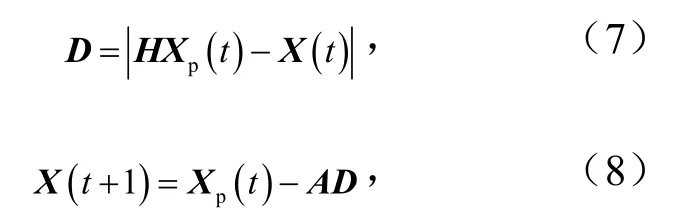
式中，A和H为系数；D为当前灰狼所与猎物的距离向量；Xp为猎物移动的位置向量.

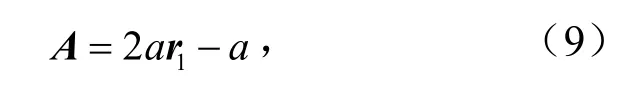
式中，随迭代次数不断增加，a从2到0递减，r1，r2是[0，1]内的随机函数向量.

图4 GWO中的位置更新 Fig.4 position updating in GWO

为更好模拟狩猎行为，假设α、β和δ对猎物的潜在地理位置有更深度了解，在每次迭代计算过程中，保留当前最优的函数解α、β和δ，然后根据它们的位置信息指导ω的移动.当前狼与其他3只狼之间的距离关系为

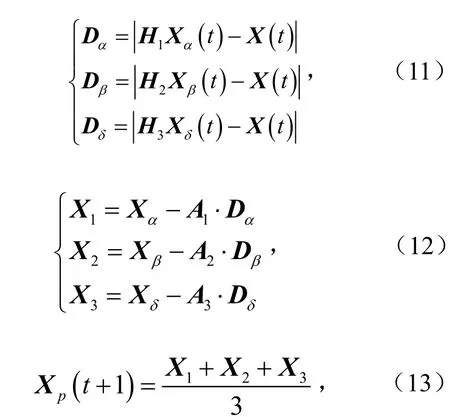
式中，Xɑ，Xβ和Xδ分别为当前儿狼群α狼、β狼和δ狼所在位置向量；Dɑ、Dβ和Dδ分别为当前狼和3只头狼的距离，m；A1，A2和A3分别为随机系数向量，t为迭代次数.

3 基于GWO-SVM的推荐算法

3.1 基于GWO-SVM的推荐方法

由于推荐系统中的大数据存在极端稀疏性现象，如果直接将SVM分类器应用到推荐系统中，将会导致分类精度严重受损，因此应对ConvMF模型推荐的实验结果进一步分类优化.在ConvMF中，已通过矩阵模型分解用户的潜在因素，降低数据的稀疏性，利用卷积神经网络提取项目的潜在因素，对用户-项目矩阵中的空缺处预测补齐.在ConvMF模型推荐结果基础上，运用支持向量机最优分类可对数据进行交叉验证和分类预测，并实现最小误差的功能.

ConvMF模型通过解决稀疏性和提取潜在特征，得到经克服稀疏性处理的评分矩阵，记为R′，定义为

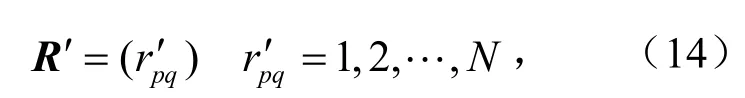
式中，m为用户数，个；n为项目组成数，个；p，q为矩阵中某个用户对某个项目q的喜好程度（类别标签或评分），p和q为1-N中任意一个数.

对问题描述如下：假设活跃项目为项目1，且前z个用户对它都作出了反馈，则用户s（1≤s≤z）的特征向量为，其类别标签为是为了使卷积矩阵分解模型达到最优，使用SVM对卷积神经网络进行分类优化，尽可能保证分类正确.

为了评估优化方法对SVM算法的分类预测效果更佳，采用相同的训练、测试样本数据，通过网格优化GS、粒子群优化PSO和灰狼优化GWO这3种优化算法分别对支持向量机的参数C和g进行优化.参数寻优方法对比见表1.

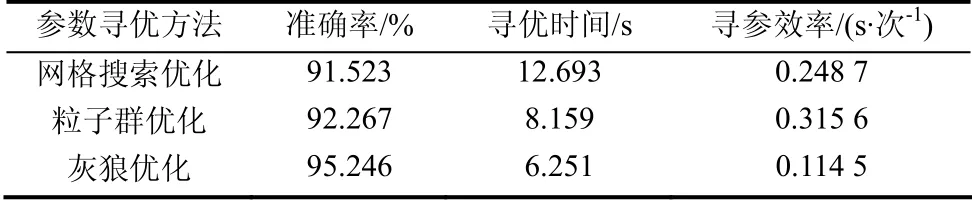
表1 参数寻优方法对比 Tab.1 comparison of parameter optimization methods

从3种算法优化支持向量机的结果看，灰狼优化算法的各项性能都要比另外两种算法好，其准确率及寻参效率都优于其余两种优化算法.粒子群优化算法收敛速度快，算法简单，但很难快速得到精确的优化结果，尤其当面对多个不同大小局部极值点的函数时，结果最为明显，受局部极值点影响大，因此其优化向量机识别的正确率不高.网格搜索耗时且识别准确率低，且寻优时存在复杂度高，运算量大等不足.而灰狼优化算法克服了粒子群优化算法惩罚参数过大而导致算法陷入局部最优的风险，相比较粒子群优化算法，网格搜索寻优时间少且寻参效率高.

由图5的GWO-SVM参数寻优过程可以看出，寻找最优的惩罚因子C为111.430 5，核参数g为0.25时，灰狼优化算法识别准确率可达到95.246%.从表1最终的预测结果准确率来看，GWO优化的支持向量机预测准确率最高.根据这3种不同优化算法对支持向量机的参数优化结果对比，灰狼优化算法相比于其他粒子群搜索算法和网格搜索算法更高效.

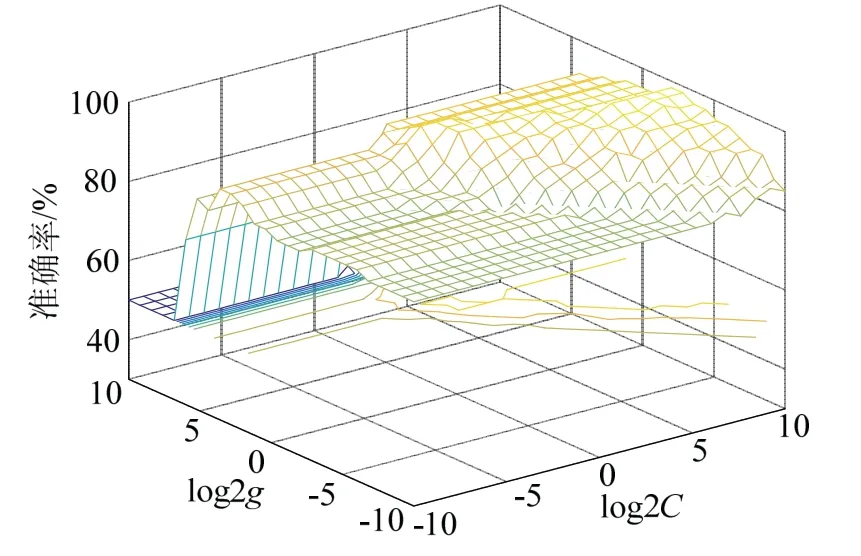
图5 GWO参数寻优过程 Fig.5 GWO parameter optimization process

3.2 推荐算法步骤

（1）输入特征向量，选取部分作为SVM的训练集，并将剩余的特征向量集作为测试集，以验证SVM识别的准确率.

（2）初始化狼群数量、迭代次数，设置惩罚因子C与核宽度g的范围.

（3）SVM根据初始参数C与g进行训练和测试，并以降低错误率为目标.

（4）GWO以C与g为猎物进行优化，随着迭代次数不断增加，越接近最大迭代次数，精度越高，数值越优，从而输出GWO全局最优值.

（5）将特征向量样本抽取一部分数据集分别作为SVM的训练集与测试集.采用最佳参数C与g建立识别模型，并对测试样本进行预测、分析.

4 实验结果与分析

4.1 数据描述

为验证所提出的基于GWO-SVM推荐算法的可行性，采用MovieLens中的ML-100k数据集作为测试本文算法性能的原始数据源，数据统计信息见表2.

表2 真实数据集的数据统计 Tab.2 statistics of real data sets

在ML-100k数据集中，用户对电影的评分为1～5的正整数，其值从小到大反映用户对每个电影的喜爱程度从低到高.由于大多数推荐系统的算法研究与测试使用都是该数据集，因此验证所提出的基于灰狼优化SVM的推荐算法可用于具有说服力.

4.2 实验结果及分析

为使效果更明显，原始943个评分矩阵经ConvMF模型处理，再从中抽取250个项目作为每个用户的测试项，其余项目作为训练数据，不仅可以使矩阵降维去噪，而且在存储空间及相似度方面也有了改善.

抽取项目个数与原始矩阵个数的比值为存储空间比值，在基于卷积矩阵分解高准确率的前提下，灰狼优化支持向量机使存储空间只占26.51%.由于任意两个项目数相似度为7.03%，表明复杂度降低，可扩展性问题得到缓解，并且减少因用户数量巨大引起的计算量.

为了更直观地得出GWO-SVM优化算法，提高推荐结果准确率，抽取的250个用户项目数，其中100个作为测试集，150个作为训练集.不同模型优化预测对比见图6.

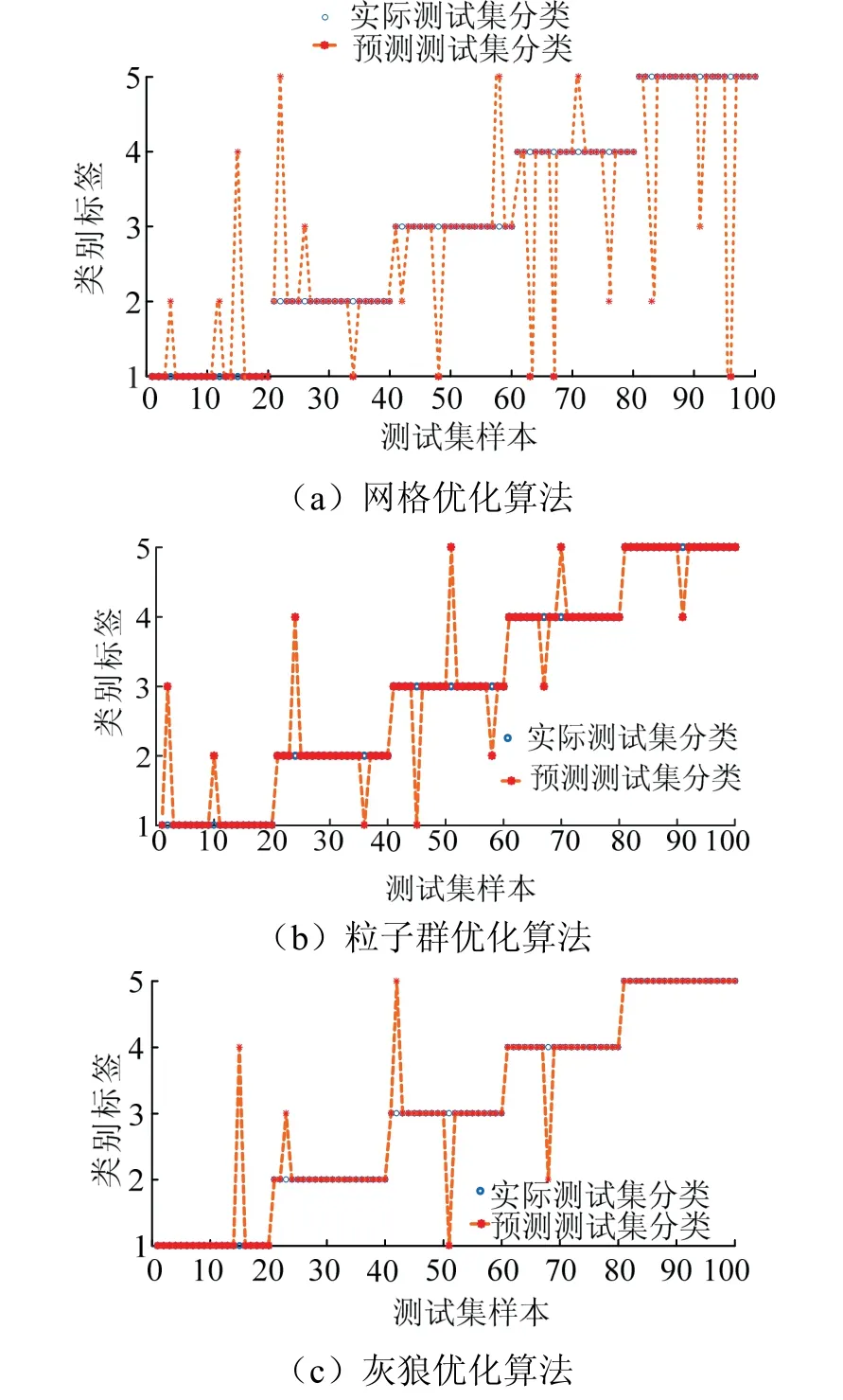
图6 不同模型优化预测对比 Fig.6 comparison of optimized prediction of different models

通过图6不同优化算法的识别对比，可以看出灰狼优化算法预测结果相比于GS-SVM和PSO-SVM识别准确率更高.对于图6的分类结果，GWO-SVM错误识别的错分点数量较少，且寻优时间及寻参效率明显优于GS与PSO，满足预设要求.

通过提取的特征向量进行模型算法对比，实验结果充分验证模型算法的可行性.通过对大量实验数据进行分析验证，结果表明，GWO-SVM算法具有较强的收敛性，可以更准确识别错分点，节省大量时间，能够在大数据层面有效提高精度和准确度.

5 结论

（1）将用户-项目评分数据转换成矩阵，采用矩阵分解对评分矩阵进行降维去噪，提高算法收敛速度，并减少训练时长.

（2）卷积神经网络从大量数据中提取出数据的隐性特征，有效解决冷启动问题，同时可对稀疏矩阵实现稠密化处理.

（3）GWO-SVM算法能够在大数据层面有效提高准确率和精度，减少算法复杂度.