基于EMD 二值化图像和CNN 的滚动轴承故障诊断
2021-03-03谷玉海朱腾腾饶文军黄艳庭
谷玉海, 朱腾腾, 饶文军, 黄艳庭
(北京信息科技大学现代测控技术教育部重点实验室 北京,100192)
引 言
滚动轴承是一种应用非常广泛的机械零件,同时也是机器中最容易出现故障的零件之一。如果能够及时、准确地对滚动轴承故障状态进行识别,对保持机器运转的稳定性和安全性具有重要意义。随着故障诊断理论研究的不断深入,学者们提出了各种故障诊断方法,例如:BP 神经网络[1]、PNN[2]、小波分析[3]、EMD[4]、集合经验模态分解(ensemble empirical mode decomposition,简 称EEMD)[5]和 奇 异值分解(singular value decomposition,简称SVD)[6]等。目前,基于机器学习的故障诊断方法主要有Logistic 回 归[7]、支 持 向 量 机(support vector machine,简称SVM)[8],人工神经网络(artificial neural network,简称ANN)[9]和模糊推断[10]。
随着人工智能的快速发展,深度学习在图像识别和语音识别等方面的应用日益广泛,在故障诊断领域的应用也越来越成为研究的热点[11]。文献[12]采用随机高斯矩阵的方法对轴承信号进行变换域压缩采集,并将处理后的信号作为深度神经网络的输入实现故障的智能诊断与识别。文献[13]采用双树复小波(dual-tree complex wavelet transform,简称DTCWT)与深度信念网络(deep belief network,简称DBN)结合的故障诊断方法对故障类型进行识别。
由于深度学习需要大量的训练数据,所以在没有足够数据的情况下难以取得令人满意的结果。CNN 是一种广泛应用于图像识别领域的深度学习网络方法并取得了优异效果,其初衷是对二维图片进行分类,不能直接用来识别一维振动数据。Peng等[14]提出了一种一维残差块,并在此基础上提出了一种新的更深层次的一维卷积神经网络(deeper one-dimensional convolutional neural network,简称Der-1DCNN)。该框架包含了残差学习的思想,能够有效学习高层次和抽象的特征,同时缓解了训练困难和更深层次网络性能下降的问题。Levent 等[15]提出了一种基于原始时间序列传感器数据的通用实时轴承故障诊断方法,该方法利用自适应Der-1DCNN分类器进行特征提取和模式识别。
如何将一维时域振动信号转换为二维矩阵或图像,是目前基于卷积神经网络的研究热点。Wen等[16]提出了一种基于51 个卷积层的调整卷积神经网 络(tweaked convolutional neural networks,简 称TCNN)故障诊断方法。将TCNN 结合迁移学习,在数据集ImageNet 上训练ResNet-50 作为特征提取器进行故障诊断。实验表明,TCNN 优于其他深度学习模型和传统方法。Chang 等[17]针对局部弱特征信息,提出了一种基于变分模态分解(variational mode decomposition,简 称VMD),SVD 和CNN 的行星齿轮特征提取与故障诊断方法。实验结果表明,该方法能够有效提取局部弱特征信息,准确识别不 同 的 故 障。Sheng 等[18]提 出 了 一 种 利 用CNN 直接对连续小波变换(continuous wavelet transform,简称CWT)进行分类的诊断方法,利用该方法在转子实验平台进行了一系列实验。结果表明,该方法能较准确地诊断故障特征。
笔者提出了一种基于EMD 二值化图像和CNN的故障诊断方法,将采集到的各类滚动轴承数据转化为特征明显的二值化图像,采用CNN 进行分类训练和识别。
1 EMD 二值化图像构造
滚动轴承数据是由轴承加速计获得,可在短期内快速获得大量的振动数据。笔者将振动数据等距划分为若干段,对每段振动数据进行EMD,对采用相关系数筛选得到的IMF 分量进行快速傅里叶变换(fast Fourier transform,简称FFT)获取频谱图,并将频谱图数据压缩成灰度图像作为CNN 分类网络训练的输入数据。
1.1 EMD 及IMF 分 量 选 择
EMD 方法是一种自适应信号时频分析方法[19],对于非线性和非平稳信号的处理具有独特优势,在海洋[20]、大气[21]及故障诊断[4]等领域得到了广泛应用。EMD 方法获得的各IMF 分量包括了原始信号不同时间尺度的局部特征,前几个IMF 分量体现了原始信号的主要特征。为保证构造的二值化图像能够有效保留原始信号的故障特征,同时避免噪声等成分的的干扰,笔者采用相关系数法筛选分解后的各个IMF 分量,使用相关系数最大的IMF 分量作为生成二值化图像的信号。相关系数的计算公式[22]为

其中:L为信号长度;ρ(i)为第i个IMF 分量与原始信号x(t)之间的相关系数。
1.2 二值化图像构造
EMD 二值化图像构造流程如图1 所示。为了满足CNN 的训练要求,需要生成具有一定特征的图片作为训练数据。首先,选取一段长度为M的振动信号进行EMD;其次,将获取的一阶IMF 分量进行FFT。假设FFT 后有2N个数据点,根据FFT 对称性,选取前N个数据点作为构造灰度图的一行。一共进行N次,得到N行数据,将N行长度为N的数据点进行堆叠,即可生成一个尺寸为N×N的灰度图矩阵。
为了避免图像对比度不足而对后续处理带来干扰,对生成的灰度图矩阵的每行进行归一化处理,并对整体进行二值化处理。归一化处理的公式为
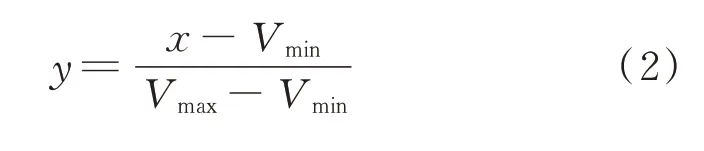
其中:x,y分别代表归一化前、归一化后的数值;Vmax,Vmin分别为原始灰度图像的最大值和最小值。

图1 EMD 二值化图像构造流程Fig.1 EMD binarization image construction process
2 CNN 网络设计
为了能够有效识别轴承故障二值化图像,需要设计合理的CNN。目前,CNN 主流的设计方式,如经典的LeNet-5 网络,其输入的二维图像先经过2 次卷积层到池化层,再经过全连接层,使用Softmax 分类作为输出层。由于LeNet-5 的网络结构设计和参数选择不适合用于本研究轴承故障二值化图像的识别,故对CNN 网络结构进行简要介绍。
2.1 输入层
输入层是整个神经网络的第1 层,也是整个卷积神经网络获取图像的途径,表示输入的一张图片的像素矩阵,在Lenet-5 原始模型框架中,输入层的图像像素为32×32。
2.2 卷积层
卷积层是整个网络最重要的组成部分,用来实现对输入的图像进行特征提取,从而获得比原始图像抽象程度更高的特征。在通过卷积层处理后,网络的节点矩阵会明显加深。卷积层特征的计算公式为
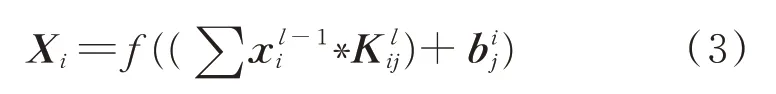
2.3 池化层
池化层通常出现在卷积层之后,二者相互交替出现,且每个卷积层都与一个池化层一一对应。池化函数常用的池化方法有最大池化、平均池化和随机池化等。池化层l中激活值的计算公式为
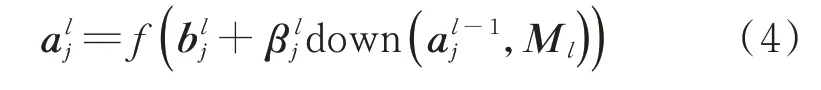
笔者采用最大池化,即选取输入图像中像素为Ml×Ml的非重叠滑动框内所有像素的最大值。池化层的作用是对图像进行降维处理,缩减图像的像素,但会增加图像的“厚度”,目的是把更多特征从图像中提取出来。
2.4 损失函数
损失函数是用来估量模型的预测值f(x)与真实值Y的不一致程度,它是一个非负实值函数,通常用L(Y,f(x))来表示。损失函数值越小,说明模型的鲁棒性越好。笔者采用的损失函数公式为
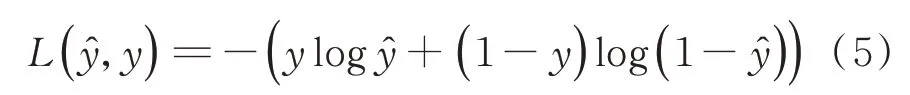
为使卷积神经网络损失函数L(ŷ,y)取得全局最小值,实质上是不断更新权值W和偏差向量b,使其取得最优值。为防止神经网络过拟合,损失函数会增加二范数项。改进后的损失函数为
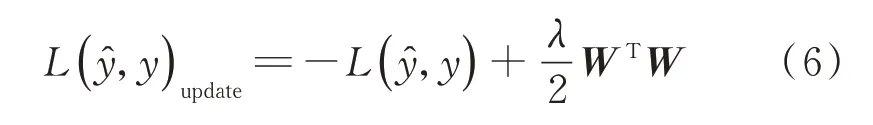
其中:λ为超参数项。
2.5 全连接层
通过卷积和池化处理之后,图像信息被抽象成更高级的图像特征,在网络的末尾由全连接层实现网络的最终分类结果。
2.6 输出层
输出层主要用来实现最终分类,通过输出层得到输入图像属于不同类别预测的概率值。
笔者采用控制变量的方式对网络进行实验,确定最终的网络结构和参数。根据CNN 设计的研究[23]以及笔者所需要识别的图像相对简单,将卷积层在2~5 层之间进行选取,卷积核主要有3×3,5×5 和7×7 共3 种,典型的激活函数主要有Sigmoid,Tanh,ReLU 和Leaky ReLU 4 种[24-25]。为 了得到更加科学有效的网络,笔者采用排列组合的方式对以上结构参数进行研究。实验分组情况如表1所示。
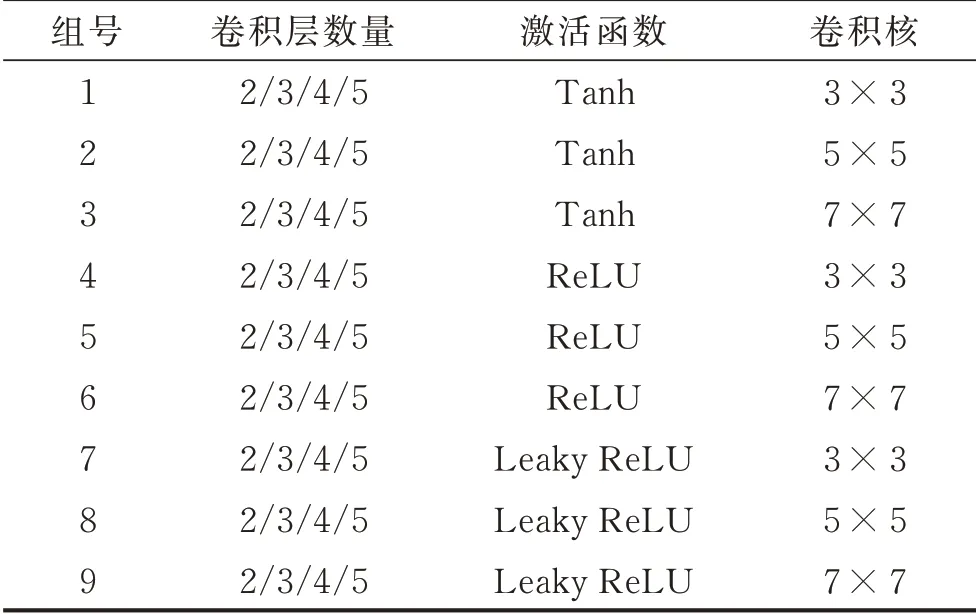
表1 实验分组情况Tab.1 Experimental grouping
3 基于EMD 和CNN 故障诊断框架
图2 为整体技术路线流程图,数据处理步骤如下:
1)将采集到的各种类型的时间序列数据进行等间隔划分,作为制作训练及测试数据集的原始样本数据;
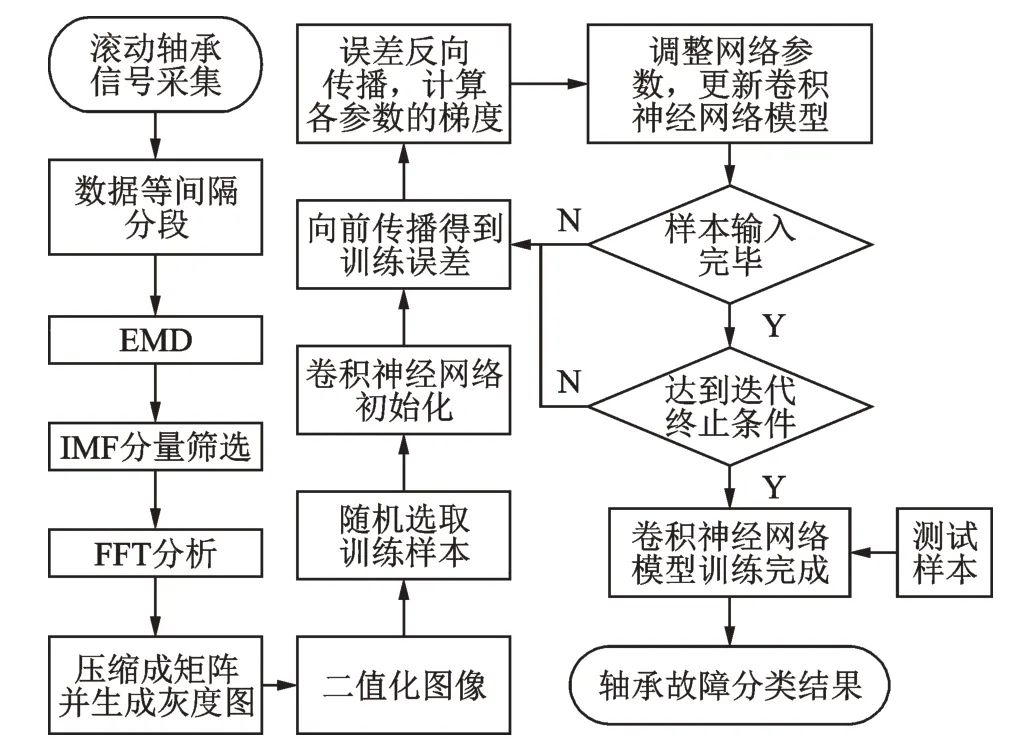
图2 笔者整体技术路线流程图Fig.2 This article overall technical route flow chart
2)采用EMD 对已经划分的各段数据进行分解,将获取的IMF 采用相关系数进行筛选,筛选相关系数最大的IMF 分量,并将IMF 分量进行FFT;
3)将每次FFT 分析后的数据值作为矩阵的一行,不断提取数据进行处理,累积构造矩阵;
4)将矩阵进行归一化处理后得到灰度图,并将灰度图像转化为二值化图像,按照以上方式将各种轴承状态的时间序列数据生成若干幅二值化图像,作为CNN 训练和测试的数据集;
5)采用生成的二值化图像数据集训练卷积神经网络,同时在训练过程中根据训练结果优化、调整网络结构和网络参数;
6)将训练好的网络对测试数据集进行测试,得出图片分类结果,从而得到数据故障分类,输出诊断结果并分析结论。
4 实验结果分析
4.1 实验数据描述
笔者使用的实验数据来源于美国凯斯西储大学轴承数据中心的轴承数据集[26]。实验平台包含功率为1492 W 的电机、转矩传感器、负载电机以及其他相关元件。采用电火花加工技术在轴承上布置了单点故障,损伤直径为0.1778 mm,损伤深度为2.794 mm。为了验证笔者所提出的方法可用于变工况下的故障诊断,在一定程度上可以克服转速差异、故障程度大小的影响,选取了3 种转速、4 种故障类型、2 种故障严重程度下的故障数据,共12 种工况的数据混合生成4 种类型的二值化图像数据集。轴承故障类型和实验条件如表2 所示。
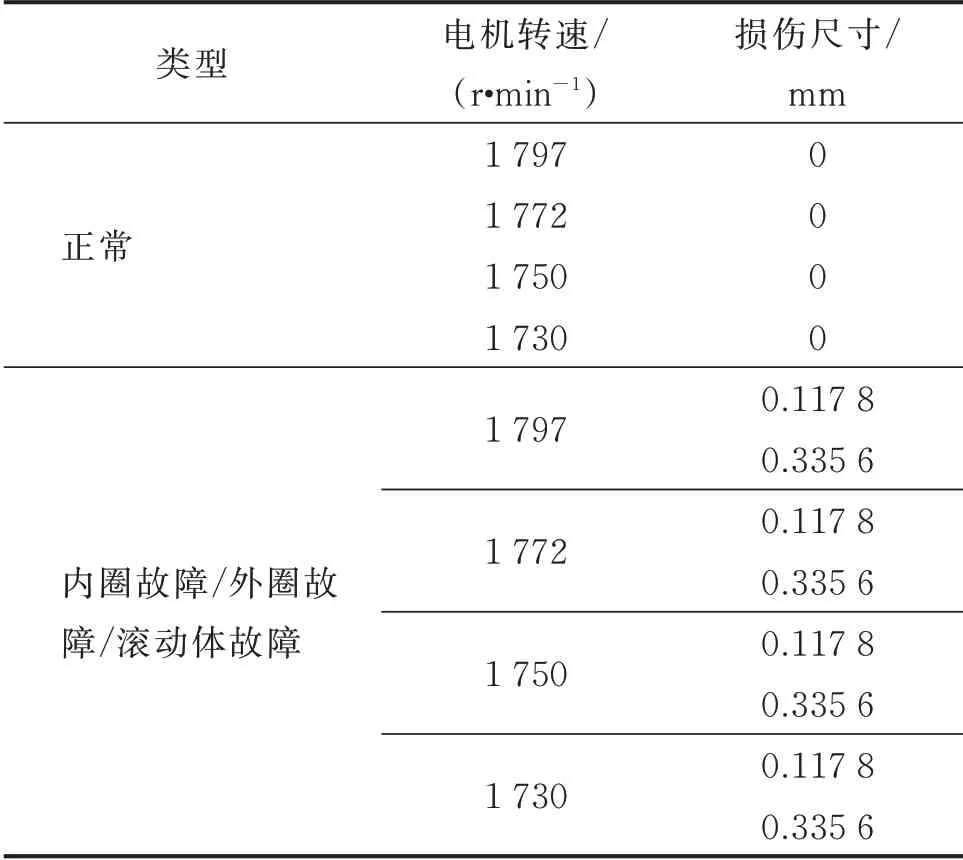
表2 轴承故障类型和实验条件Tab.2 Bearing failure types and test conditions
由于采用不同长度的振动信号生成的二值化图像像素不同,所体现出的特征效果也不同,所以需要经过实验确定图像像素。笔者分别采用长度为32,64,128 和256 共4 种情况下的振动信号生成的二值化图像进行对比,将特征效果最明显的二值化图像像素点数量作为网络训练和测试的最终像素点数目。根据二值化图像构造方法,长度为32,64,128和256 的信号分别可以构造出像素为16×16,32×32,64×64 和128×128 的二值化图像,分别使用正常状态、外圈故障、内圈故障和滚动体故障的数据进行实验。16×16,32×32 这2 种像素的二值化图像由于像素点太少,图像特征非常不明显,完全无法 区 分4 类 状 态。像 素 为64×64,128×128 这2 种二值化图像都能较好地区分4 种状态。由于构造一张像素为16×16 的二值化图像需要8192 个原始振动信号数据点,而构造一张像素为128×128 的二值化图像则需要32768 个原始振动信号数据点,所以在相同长度振动信号的情况下,构造一张像素为128×128 的二值化图像可以构造4 张像素为64×64 的二值化图像。在相同数量原始信号的条件下,如果能构造出更多的二值化图像数据,则有利于CNN 的训练和识别。 因此,虽然像素为128×128 的二值化图像特征更加明显,综合考虑,笔者最终采用像素为64×64 的二值化图像作为CNN 训练和测试的图像像素。
像素为64×64 的二值化图像示例如图3 所示。可以看出,经上述方法构造的4 种不同状态的轴承数据的灰度图像具有明显特征。

图3 像素为64×64 的二值化图像示例Fig.3 Examples of binary images with 64×64 pixels
4.2 实验数据处理
笔者进行的各项实验均由Matlab 2015b 和Spyder 2 种软件完成。使用Matlab 2015b 对信号进行EMD,筛选出相关系数最大的IMF 分量进行FFT,求得时频数据并生成矩阵。导入TensorFlow 和OpenCV 的Spyder 软件,将时频数据矩阵归一化并生成最终的二值化图像,使用Spyder 对图片进行训练和测试,通过TensorBoard 可视化工具查看准确率、损失函数等曲线的变化。计算机硬件和软件的配置参数如表3,4 所示。

表3 硬件配置环境参数Tab.3 Hardware configuration environment parameters
根据表2 所示的数据,一共生成4 种状态下的433 张二值化图像。将图像进行随机分配,训练集和测试集的分配数量如表5 所示。
表4 软件配置环境参数Tab.4 Software configuration environment parameters
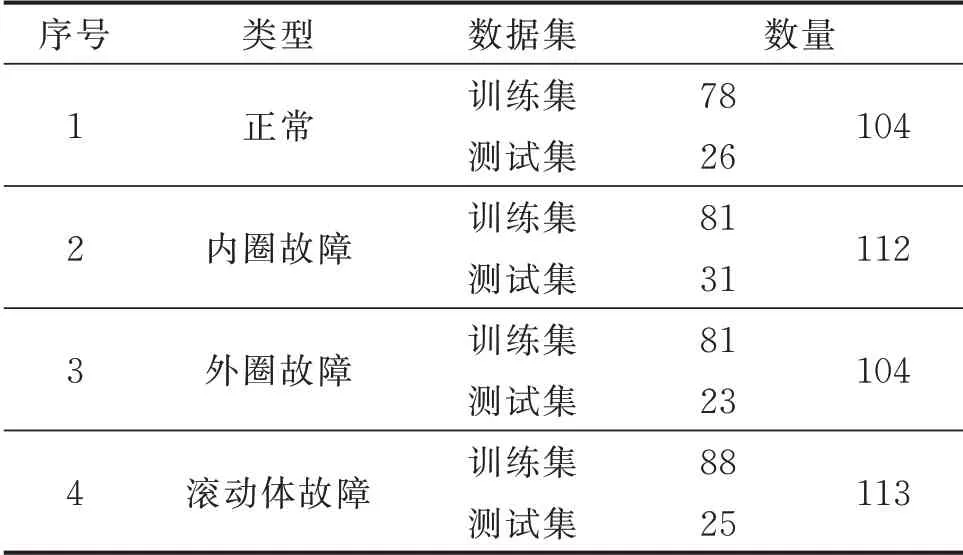
表5 训练集和测试集分配数量Tab.5 Training set and test set allocation
通过使用表5 中分配的数据集对表1 中设计的各组网络进行逐一训练、测试对比,最终确定了输入图像的像素为64×64,卷积层为4 层,使用7×7卷积核。采用Leak ReLU 作为激活函数的CNN 模型,将全连接层之后的分类输出结果调整为4 类。笔者设计的网络模型如图4 所示,网络模型的训练和测试曲线如图5 所示。
在训练中一个迭代次数是指所有的数据送入网络中完成一次前向计算及反向传播的过程。准确率反映了模型正确识别的图像个数。损失率是用来估量模型的预测值与真实值的不一致程度。准确率越大、损失率越小,说明模型的识别能力和鲁棒性越好。从图5 可以看出,无论训练还是测试,其准确率曲线的上升速度和损失曲线的下降速度都非常迅速,经过100 轮迭代次数后,最终的训练准确率、训练损失率、验证准确率和验证损失率的值分别为97.56%,4.4736×10−3,96.69%和0.01021。
4.3 与传统方法对比及抗噪性能测试
为了验证笔者提出的方法比传统故障诊断方法更能有效识别轴承的故障类别,将此方法与参考文献[27]中采用BP 和概率神经网络(probabilistic neural network,简称PNN)方法的分类准确率进行对比,如表6 所示。
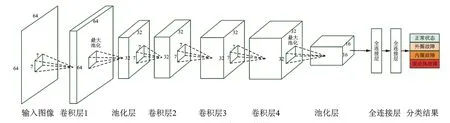
图4 笔者设计的网络模型Fig.4 The network model designed in this paper
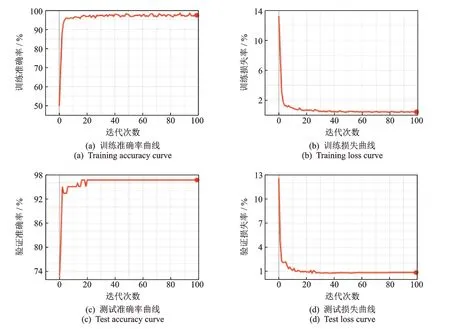
图5 网络模型的训练和测试曲线Fig.5 The training and testing curves of the network model are finally determined
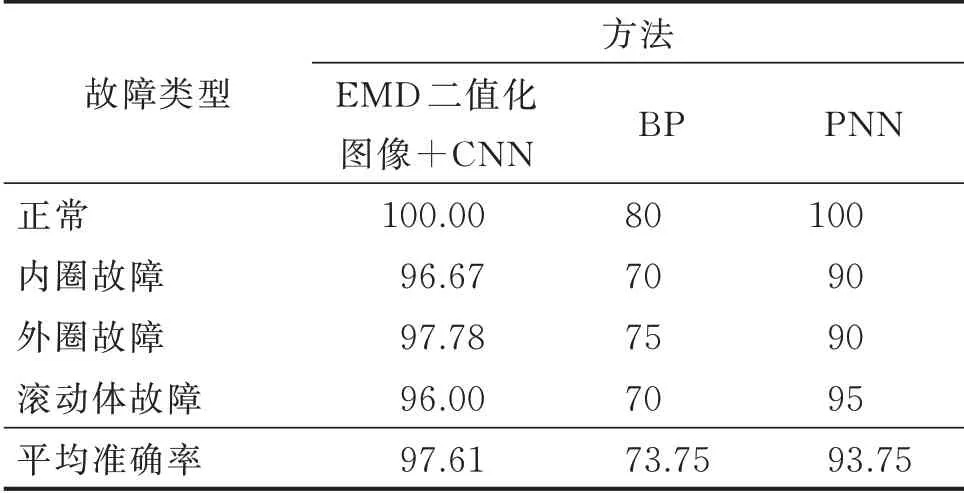
表6 平均分类准确率对比Tab.6 Comparison table of average classification accuracy %
通过表6 可以看出,笔者提出的方法能够实现很高的准确率。在正常状态下,图片的正确分类准确率最高,为100%,这是由于正常状态下的滚动轴承二值化图像的特征非常明显,容易被CNN 分类器识别。内圈故障和滚动体故障状态下的图片相似度较高,在识别过程中混淆相对较多,准确率相对较低,但也达到了96%以上。故障分类平均准确率达到了97.61%,能够有效检测各类故障。笔者提出的方法识别效果都远优于传统的BP 和PNN 方法的准确率,具有更好的泛化能力。
为了测试笔者所提出算法和模型的抗噪性,在4 种状态下的轴承振动信号中加入6dB 的白噪声。图6 为原始信号和加入6dB 白噪声后的信号对比。可以看出,在加入白噪声后的波形出现了一些毛刺,没有原始信号显得平滑。图7 为加噪后的二值化图像示例图。可以看出,正常状态下的轴承信号加噪后生成的二值化图像中出现了一些噪点,但左侧的白色亮带依然很明显,未受到太大影响;其他3 种状态下的轴承信号在加噪后几乎没有出现噪点。这也证明了笔者所提出的方法本身具有一定的抗噪能力。在抗噪性能测试中,分别在4 种状态下的训练集和测试集中各加入15 张加噪的图像,图8 为加噪前后准确率和损失曲线对比。可见,2 种曲线的整体变化趋势非常接近。加噪后最终识别的准确率略有降低,测试准确率达到了96.19%,略低于未加噪的测试准确率值97.61%,这说明加入的噪声图像对网络产生影响非常小,证明了笔者所设计的CNN 网络模型具有很强的鲁棒性和抗噪能力。
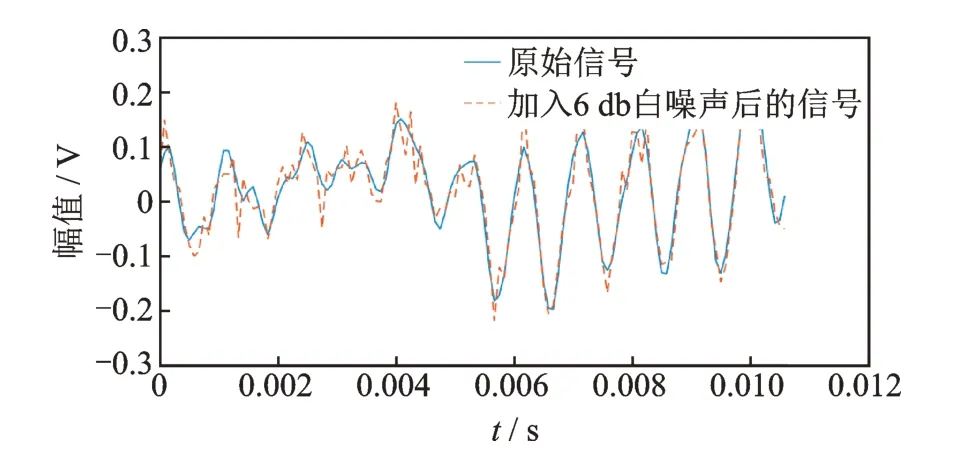
图6 原始信号和加入6db 白噪声后的信号对比图Fig.6 The original signal and the signal after adding 6db white noise

图7 加噪后的二值化图像示例图Fig.7 A sample image of the denoised binary image
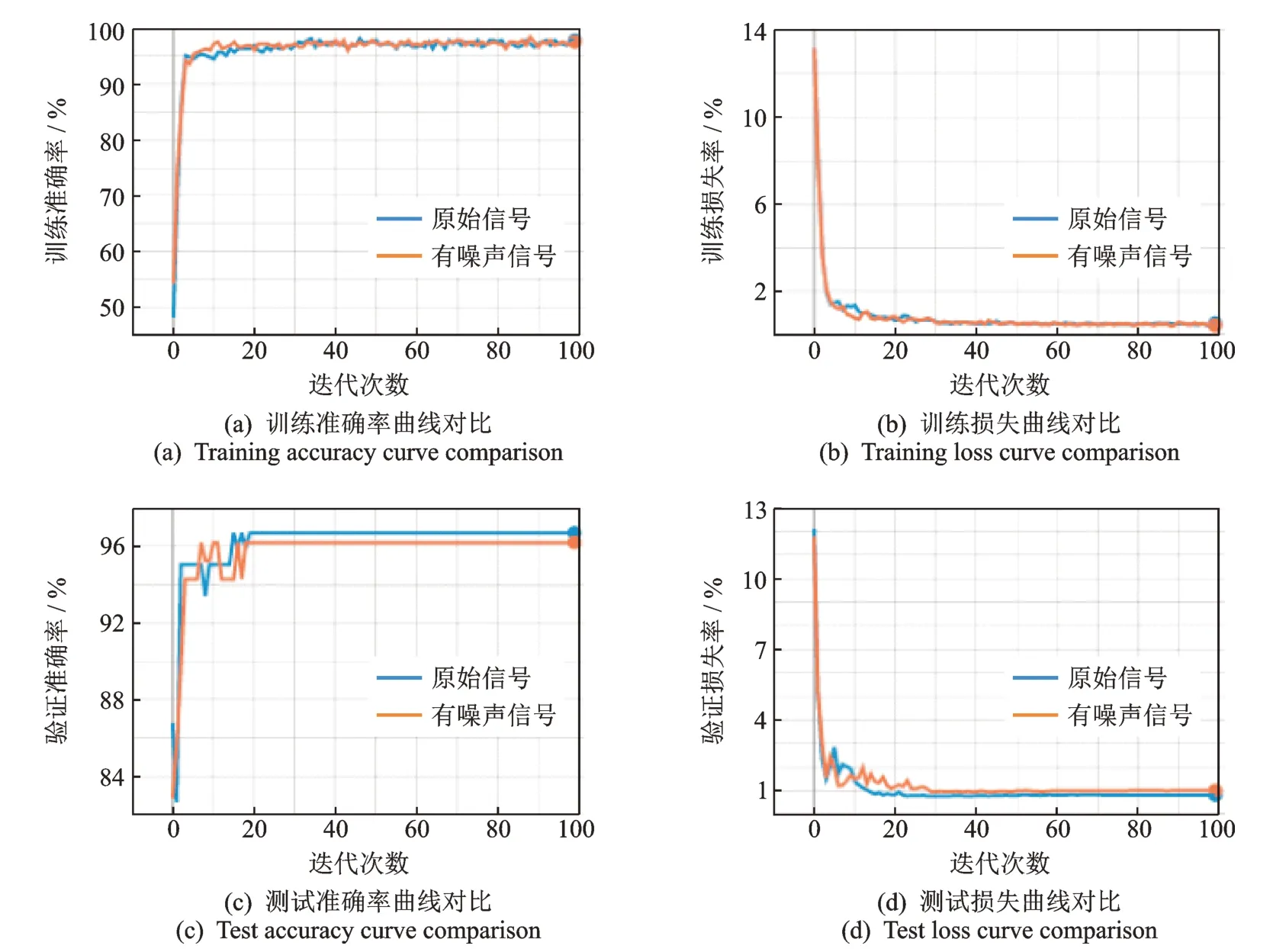
图8 加噪前后准确率和损失曲线对比Fig.8 Comparison of accuracy and loss curves before and after noise addition
5 结束语
提出了一种基于EMD 二值化图像和CNN 的智能故障诊断方法,将振动信号转化为具有明显特征的二值化图像。在CNN 设计方法的基础上,根据训练要求设计了36 种CNN 网络结构。通过实验数据集测试,确定了一种最优的CNN 网络模型。笔者采用的基于EMD 二值化图像和卷积神经网络的滚动轴承故障诊断方法整体上能够达到97.61%的识别准确率,远超过传统的BP 方法的识别准确率73.75% 和概率神经网络方法的识别准确率93.75%,在抗噪能力测试中达到了96.19%的识别准确率,体现了优异的抗噪能力和鲁棒性,证明了笔者所提出方法的可行性,为采用CNN 进行故障诊断提供了新的思路,具有较好的技术应用前景。
