双频振动系统下空心轴下料寿命模型∗

化春键， 任皓靖， 陆云健

（1.江南大学机械工程学院 无锡，214122） （2.江苏省食品先进制造装备技术重点实验室 无锡，214122）

引 言

复合频率振动低应力加载技术通过复合频率的叠加振动加载。低频加载振幅较大，形成疲劳裂纹；高频加载频率高，振幅较小，使疲劳裂纹持续扩展［1-2］，最终能够加快疲劳裂纹的扩展速率，提高断面质量。将此技术应用于下料，可实现低周精密可控性下料，解决了常规下料方法裂纹扩展速率低、断面质量差等问题［3-4］。空心轴常用于轴类构件的轻量化设计，在工程实际中应用越来越普遍［5］。基于文献［2］提出的复合频率振动低应力加载技术，笔者研究了复合频率振动下空心轴的下料寿命模型。复合频率振动低应力加载技术需要建立断裂过程的下料寿命模型，在小范围屈服的条件下，SIF 是研究此技术的一个重要参数［6-7］。

针对复合频率振动下预置V 形切口的空心轴下料寿命、几何参数及加载状态之间的关系，笔者推导出复合频率振动下的带V 形切口的空心轴下料裂纹尖端应力强度因子计算式，在此基础上，建立双频振动系统下带V 形切口的空心轴下料寿命与其几何参数的模型，分析得到影响规律，并设计试验验证了该规律。

1 带V 形切口的空心轴裂纹尖端的SIF 值计算

如图1 所示，带V 形切口的空心轴的几何参数包括切口深度h、张角α、切口处曲率半径ρ、V 形切口处截面半径a、空心轴外径b、空心轴内径d以及切口间距L。

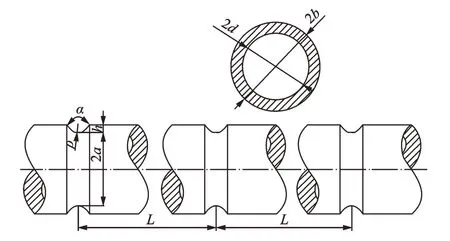
图1 带V 形切口的空心轴几何参数示意图Fig.1 Diagram of geometric parameters of V-groove hollow shaft

文献［8］分析了空心轴V 形切口根部处于三相应力状态时，其应力场分布［8］为

其中：σx，σy，σz分别为空心轴V 形切口根部x，y，z方向上的应力；r，θ为空心轴V 形切口根部坐标系的极坐标；μ为泊松比；τ为剪切应力。

文献［9］根据V 形切口根部的应力场分布公式，推导其几何形状系数公式，修正后为

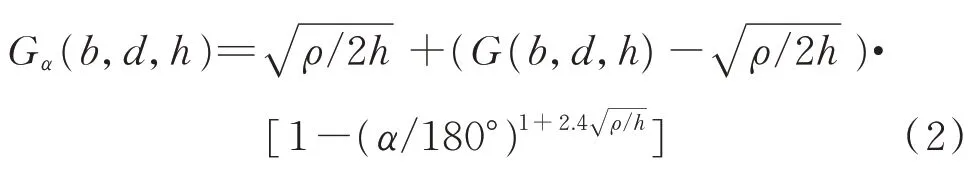
在本加载状态下，空心轴主要为张开型裂纹状态。式（2）中，无量纲值G（b，d，h）为具有环形裂纹空心轴的修正系数，G（b，d，h）的取值［10］如图2 所示。图2 中，横坐标为空心轴V 形切口深度与轴壁厚之比为h/（b−d），其为无量纲值，针对的是平均半径与壁厚之比不同的空心轴（b+d）/2（b−d）。

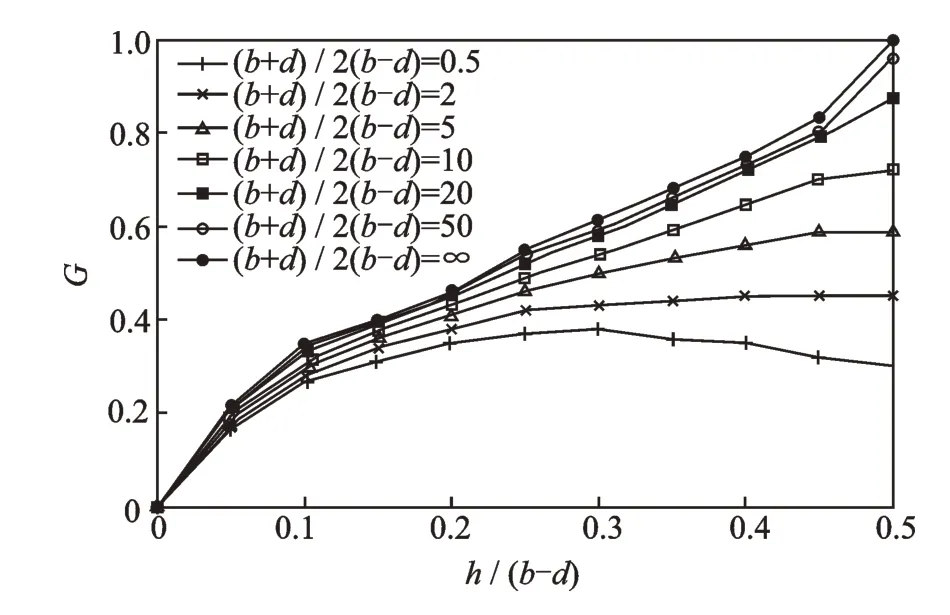
图2 具有环形裂纹空心轴修正系数取值Fig.2 Correction coefficient value of hollow shaft with annular crack

空心轴V 形切口处SIF［11］可以表示为

其中：σ为空心轴V 形切口处所受名义应力值。

在空心轴V 形切口处张开型裂纹状态下，裂纹沿着V 形切口所在截面垂直中性轴的方向扩展。

2 复合频率振动下空心轴V 形切口尖端处SIF 值计算

在复合频率振动下，空心轴V 形切口尖端处所受应力较为复杂，无法直接代入式（3）。笔者通过应力谱的编制，将其所受的复杂应力转化为多级等幅应力。本研究搭建的双频振动系统机械部分［2］组成如图3 所示。机械部分由2 个变频电机分别给2 对偏心块提供不同频率的转速。小变频电机的减速比为2∶1，大变频电机的减速比为1∶1。一对小偏心块产生高频载荷，一对大偏心块产生低频载荷。2 对上下对称排列的大、小偏心块通过激振体为空心轴提供复合频率振动的加载。图4 为空心轴振动示意图，空心轴一端在夹具上固定，激振体带动空心轴另一端在导轨上做复合频率的振动。

图3 双频振动系统机械部分Fig.3 Dual-frequency vibration device mechanical part

图4 空心轴振动示意图Fig.4 Hollow shaft vibration diagram

空心轴受到单频振动时，系统的动力学模型为

其中：m为激振体的质量；m1为小偏心块的偏心质量；ω1为小偏心块转动的角速度；d1为小偏心块的偏心距；c为系统阻尼；k为系统刚度。

瞬态解在本系统中没有意义，故不做讨论，仅需要讨论稳态解。

振幅历程公式为

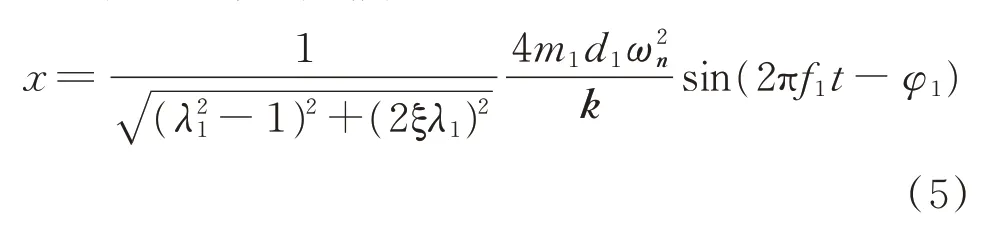
笔者选择线性递减单频振动的加载方式，单频振动下的线性递减变频曲线如图5 所示。振幅检测部分采用加速度传感器，配合多功能数据采集系统和压电传感器，确保得到的振幅数据的准确性。在线性递减的单频加载方式下，通过振幅检测部分得到铝合金空心轴的振幅历程图，如图6 所示。

为了得到幅频曲线，在Matlab 中将振幅历程图进行傅里叶变换，得到幅频曲线如图7 所示。

图5 单频振动下的线性递减变频曲线Fig.5 Linear decreasing frequency conversion curve under single frequency vibration

图6 单频振动下铝合金空心轴的振幅历程图Fig.6 Amplitude history diagram of aluminum alloy hollow shaft under single frequency vibration

图7 振幅历程图的傅里叶变换幅频曲线Fig.7 Fourier transform of amplitude history diagram

由于本研究振幅的均值波动不大，因而采用波动中心法来编制适用于本研究系统的一维振幅谱。为了便于统计，采用各级振幅组中值来表示其振幅幅值，并用小波处理滤掉不产生疲劳损伤的次要振幅。本研究小波处理的门槛值设为0.75 mm，得到双频振动系统一维多级振幅谱如表1 所示。

根据材料力学相关知识，空心轴V 形切口尖端处所受名义应力关系式为

其中：M为空心轴所受力矩；l为受力力臂的长度，与本研究设备下空心轴的加载位置有关；EI为截面的抗弯刚度；x为空心轴的振幅，即双频振动系统的振幅。

表1 双频振动系统一维多级振幅谱Tab.1 One-dimensional multi-level stress spectrum of dual-frequency vibration system

式（6）中，令φ=8EI/π(al)3，将一维多级振幅谱转化为V 形切口尖端处所受一维多级应力谱。

V 形切口尖端处所受等效的等幅名义应力公式［12］为

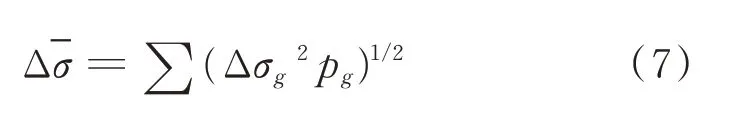
将上述方法推广到复合频率振动的加载方式，以双频为例，当棒料受到双频振动时，根据系统的动力学模型，双频振动下的振幅历程公式为

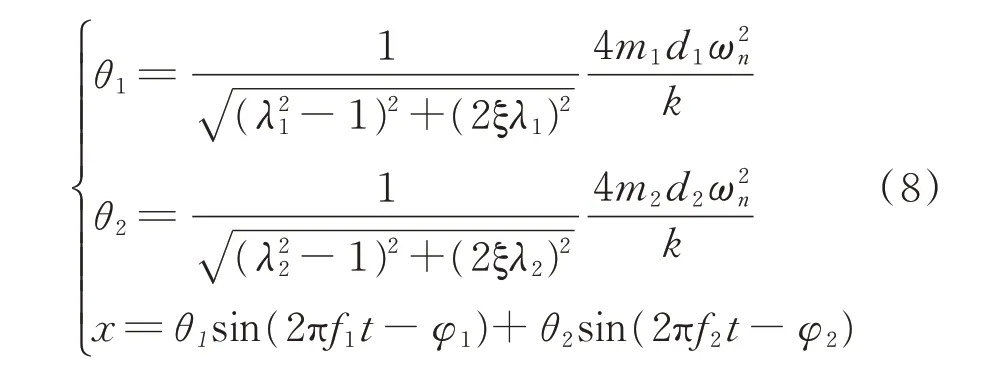
双频振动加载选择线性递减的低频振动，并叠加恒频的高频振动加载方式，双频振动下的叠加变频曲线如图8 所示。通过振幅检测设备，得到双频振动下铝合金空心轴的振幅历程，如图9 所示。

同理，将振幅历程图转化为一维多级振幅谱，再将一维多级振幅谱转化为V 形切口处所受一维多级应力谱，最后得到双频振动下V 形切口处所受等效的等幅名义应力。当同一种类别的裂纹处于若干个载荷共同作用的情况下，可以先求解得到各个载荷单独作用下的SIF，将各个载荷作用下的SIF 值进行相互叠加［13］，获得多种类型载荷共同作用下的SIF 值。复合频率振动下空心轴的V 形切口处SIF值计算公式为

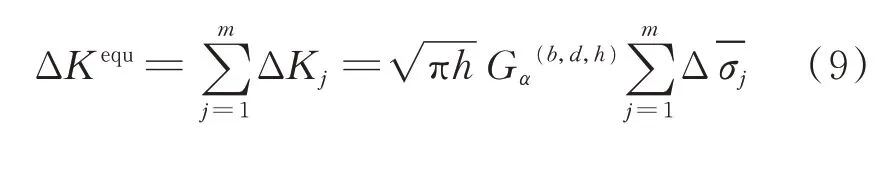
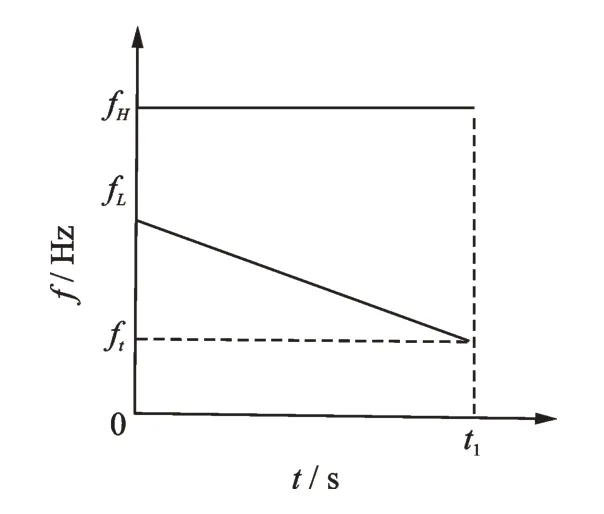
图8 双频振动下的叠加变频曲线Fig.8 Superposition conversion frequency curve under dual frequency vibration

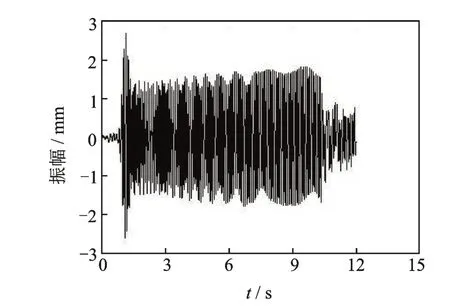
图9 双频振动下铝合金空心轴的振幅历程Fig.9 Amplitude history diagram of aluminum alloy hollow shaft under dual frequency vibration

3 复合频率振动下带V 形切口的空心轴下料寿命模型

笔者选用基于低周疲劳行为和Ⅰ型裂纹尖端RKE（Rice-Kujawski-Ellyin）奇异场，并考虑近门槛区短裂纹行为的疲劳裂纹寿命公式［14］为

其中：h0为初始裂纹尺寸；hc为临界裂纹尺寸；ΔKth为裂纹扩展门槛值；n'为应变硬化指数；σc为屈服应力。

将式（3）代入式（10），积分式采用多段插值型数值积分。由于插值型数值积分的误差来源于对原式的二次求导，因而划分段数足够多，误差可以忽略不计。结合式（2）和式（9），得到基于双频振动系统复合频率振动下的下料寿命模型为

根据K 判据［15］，当ΔK=ΔKIC，得到下料寿命模型中的断裂临界裂纹尺寸（积分上限）hc为

其中：ΔKIC为断裂韧度；式（11）中第n+1 段的裂纹深度hn+1即为式（12）中临界裂纹尺寸hc。

式（11）建立了复合频率振动下下料寿命与带V形切口空心轴的几何参数以及加载状态之间的模型。可以看出：下料寿命与复合频率振动下V 形切口尖端处所受等效名义应力幅值有关，复合频率振动下V 形切口尖端处所受等效名义应力是各个单一频率振动下V 形切口尖端处所受等效名义应力的累加，由于累加后的数值一定会更大，因而复合频率的振动加载方式会大幅缩短下料寿命，加速裂纹的扩展。由于空心轴的弹性模量E与V 形切口尖端处所受名义应力正相关，因而模型中弹性模量E与下料寿命也是正相关。

在模型中，b-d为空心轴壁厚，这里b取12 mm，随着d的减小，空心轴壁厚会增大，结合图2，G（b，d，hi）会减小，因而下料寿命会增大。V 形切口张角α越小，下料寿命越短，这对整个模型的数值结果影响极小。由于V 形槽的张角对槽底应力集中的影响程度很小，故一般V 形槽夹角选取90°，以适应棒料 两 端 车 削45°倒 角 的 需 求［16］。h对 应V 形 切 口 深度，以b=6 mm，d=3.6 mm，ρ=0.2 mm，α=90°的空心轴为例，分析了此因素对模型的影响，此时空心轴平均半径与壁厚之比为2，得到V 形切口深度对模型影响关系，如图10 所示。

由图10 可知，预置的切口深度越深，Y值会越大，因而下料寿命越短。为了分析切口处曲率半径ρ对整个模型的影响，同样以b=6 mm，d=3.6 mm，h=1 mm，α=90°的空心轴为例，得到V 形切口处曲率半径对模型的影响关系，如图11 所示。

图10 V 形切口深度对模型影响关系Fig.10 Relation chart of effect of V-shaped incision depth on model

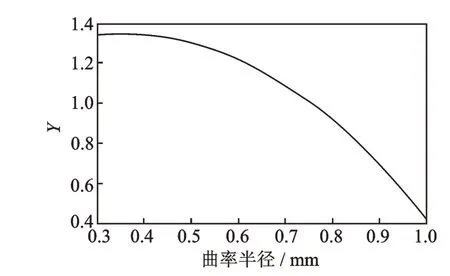
图11 V 形切口处曲率半径对模型影响关系Fig.11 Relation chart of effect of curvature radius at the Vshaped incision on model

由图11 可知，随着切口处曲率半径增大，Y值减少，因而下料寿命变长。hn+1（hc）为临界裂纹尺寸，临界裂纹尺寸受断裂韧度ΔKIC、加载大小以及带V 形切口空心轴的几何形状修正系数G(a/b)α影响，随着偏心块级数增大，会使下料时临界裂纹尺寸提前到来。

4 试 验

为了验证寿命模型规律的正确性，笔者设计了双频振动下料试验。综合考虑低应力加载技术［17］和双频振动系统的实际情况，选用45 钢和铝合金空心轴，b取6 mm。通过双频振动系统的偏心块级数，确立双频振动加载大小，偏心块级数根据裂纹萌生条件确定［3］。

对不同几何参数的带V 形槽空心轴进行振动加载试验。由于试验中频率控制曲线不变，因而下料寿命可近似看作下料时间。通过试验得到几何参数不同的空心轴下料时间，如图12 所示。

从图12（a）可以看出，对于45 钢和铝合金空心轴，相比于单频振动加载方式，双频振动下的下料时间会大幅减少，不论单频还是双频的加载方式，45 钢空心轴下料时间都大约为铝合金的3 倍。从图12（b）可以看出，其他几何参数不变，随着空心轴V 形切口深度的增加，下料时间会逐渐减少，且对于V 形切口处张角分别为60°，75°，90°，105°和120°的空心轴来说，下料时间会随着V 形切口处张角的增大而延长。从图12（c）可以看出，下料时间与空心轴的壁厚和内径也有关系，其他几何参数不变，当空心轴壁厚分别设为1.4，1.8，2.2，2.6，3.0 和3.4 mm 时，下料时间与空心轴壁厚为正相关的关系。综上可知，上述试验结果与笔者下料寿命模型分析得到的规律一致。

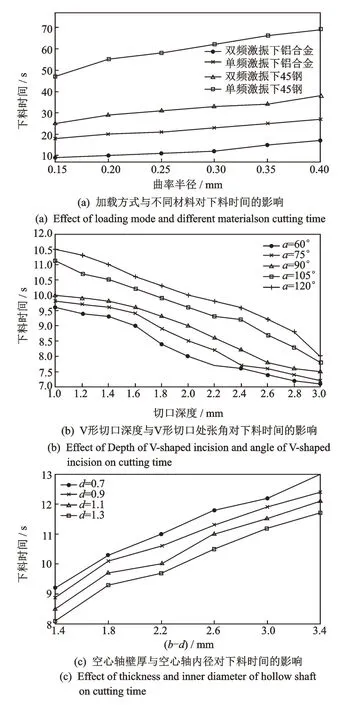
图12 几何参数不同的空心轴下料时间Fig.12 Cutting time of hollow shaft with different parameters

5 结 论

1）将复合频率振动下空心轴的V 形切口尖端处所受的复杂应力转化为一维多级应力谱，通过式（7）转化为V 形切口尖端处所受等效的等幅名义应力。

2）通过复合频率振动下V 形切口尖端处SIF值与空心轴几何参数之间关系，建立复合频率振动下的下料寿命模型，分析该模型规律并设计试验，得到的试验结果与模型规律一致。