盾构竖井垂直顶升施工阶段隧道变形分析

徐世杨， 刘叔灼， 陈俊生， 杨春山

（1.华南理工大学土木与交通学院，广州 510641； 2.广州市市政工程设计研究总院有限公司，广州 510060）

盾构竖井垂直顶升法指在已建隧道内部，通过液压千斤顶等设备，将竖管朝上闷顶并穿出土层，形成竖向工作井. 相对于传统的地面往下大开挖施工，该工法因其工期短、对环境影响小等诸多优点［1］，近年来得到了越来越多的应用［2］. 垂直顶升施工不可避免会对隧道结构产生影响，确定竖井垂直顶升诱发的隧道结构变形特征，是合理选择加固措施，顺利实现顶升的前提. 然而现有的研究成果主要集中在施工工艺［3］和结构设计［4-5］上，对垂直顶升阶段隧道所受影响却鲜有研究. 因此对盾构竖井垂直顶升施工阶段隧道的变形进行分析是十分必要的.

针对垂直顶升施工诱发的隧道结构变形问题，借助三维数值法，分析盾构竖井垂直顶升阶段隧道管片变形和环缝接头变形规律，并通过理论计算验证数值模型的合理性，此外还探讨不同顶升反力作用对管片和接头变形特性的影响.

1 工程概况

广州某盾构隧道，隧道顶面覆土为6 m，隧道衬砌采用C50 钢筋混凝土，外直径6 m，管片厚度0.3 m，幅宽1.5 m. 管片之间接头和环间接头均采用M24 螺栓连接. 其中，每环纵缝采用12根M24连接，每个环缝采用10根M24连接. 隧道内采用竖井垂直顶升闷顶法，断面图如图1所示. 竖井井壁厚度为0.2 m，外径为1.8 m，环宽为1.5 m. 垂直顶升法施工顺序为：顶升装置就位→将第一节管节与顶盖连接、在管节周围设置止水装置→顶升第一节→固定第一节管节并设防回落措施→之后管节依次接入、顶升. 顶升流程如图2所示.

图1 垂直顶升施工阶段断面Fig.1 Section of shaft vertical jacking construction

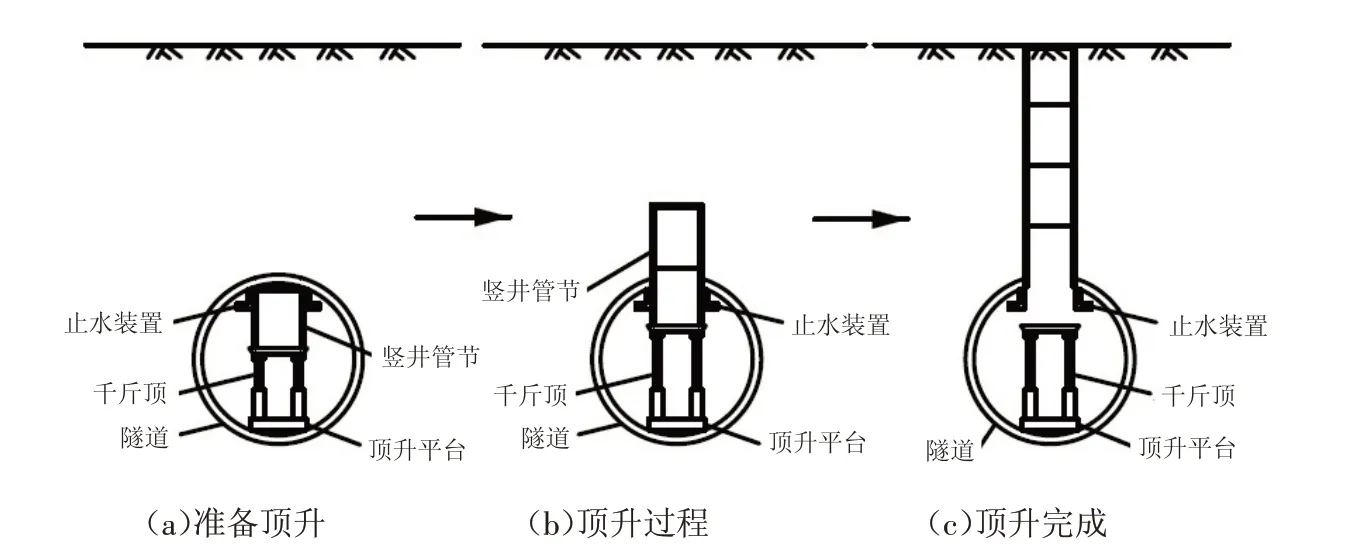
图2 盾构竖井垂直顶升流程Fig.2 Process of shield shaft vertical jacking

2 隧道变形计算模型

以上述工程实例为研究对象，利用有限元软件建立一段具有12环通缝拼装管片的盾构隧道三维有限元模型，来探讨盾构竖井垂直顶升施工引起的隧道接头和管片的变形规律.

2.1 隧道结构模型

模型沿环向引入环向等效刚度系数η 将隧道简化为均质环，沿纵向环与环则通过纵向螺栓加以连接，如图3 所示. 根据吴庆等［6-7］研究成果，η 取为0.7. 管片和纵向螺栓均采用实体单元模拟，管片间连接通过将纵向螺栓嵌入2个相邻的管片中来模拟，管片间设置接触面［8-9］建立联系. 隧道与土之间的相互作用通过引入地层弹簧k［10］来实现，根据隧道所处地层，基床系数k取为10 000 kN/m3，地层弹簧采用仅受压的沿着衬砌全周布置的曲面弹簧模拟.

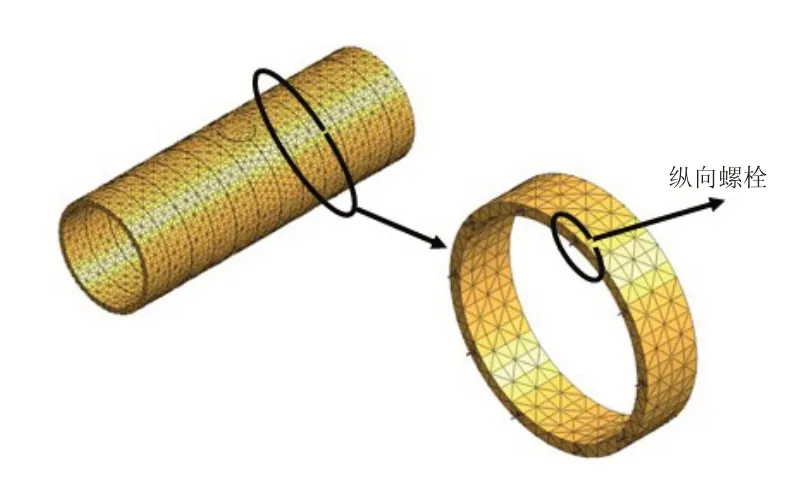
图3 隧道结构计算模型Fig.3 Calculation model of tunnel

2.2 材料参数

将地层概化为单一土层进行计算，土层物理力学参数如表1所示. 隧道管片结构实际参数如表2所示.竖井与管片的参数一致. 本模型采用直螺栓模拟实际结构的弯螺栓，所以弹性模量取为5.4×104MPa［11］.

表1 土样物理力学参数表Tab.1 Physico-mechanical parameters of soil

表2 隧道管片实际结构参数Tab.2 Structural parameters of shield segments

2.3 计算荷载

竖井垂直顶升阶段隧道衬砌承受的荷载主要是水、土压力和顶升反力. 受荷模型如图4所示.

图4中，Py1为管片环顶部的上覆水土压力；Py2为管片环底部的土层抗力；Py3为管片的自重；Px1为管片环顶部水平面上的侧向水土压力；Px2为管片环底部水平面上的侧向水土压力.隧道埋深为6 m. 隧道埋深为1 倍隧道外径，所以不考虑土拱效应［12］. 土压力计算公式如下：

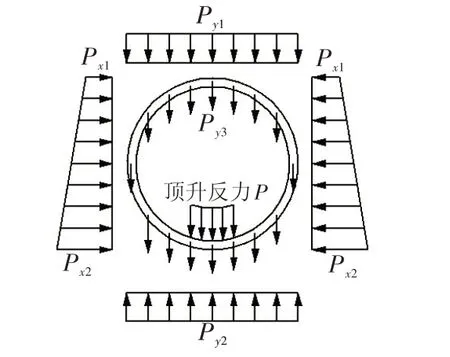
图4 垂直顶升阶段隧道受荷模型Fig.4 Loading model of tunnel under vertical jacking

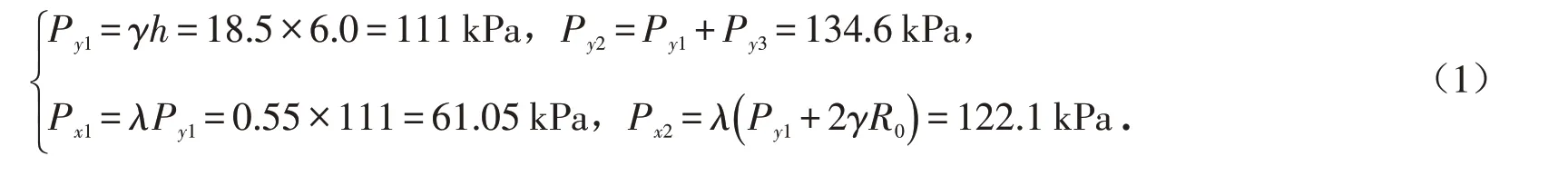
式中：h 为隧道埋深，γ 为土层重度；R0为隧道外半径；λ为侧向土压系数，根据地质条件及经验系数［11］，取为0.55.

顶升反力通过反力垫块传递到隧道底部，根据文献［13］得到顶升反力P的最大值约为120 t. 在计算中将顶升反力P 以均布力的形式对称施加在开口环底部约2 m×2 m 矩形区域的管片上.

2.4 施工工况

针对实际施工情况，将垂直顶升施工阶段分为以下工况（详见表3）. 不同工况对应的有限元模型如图5.

表3 模型计算工况Tab.3 Working conditions for model calculation

图5 不同工况对应的模型图Fig.5 Models of different working conditions

3 计算结果分析

3.1 隧道管片变形分析

图6给出了不同工况隧道整体竖向位移云图和开口环、相邻环的椭圆度变化情况. 由图中可以看出，工况2与工况1相比，隧道整体的竖向沉降增大. 管片最大竖向位移发生在开口环的顶部，开口环顶部沉降值在工况1时为8.67 mm，在工况2时为9.76 mm，较工况1时增加了1.09 mm. 工况3与工况2相比，由于隧道底部顶升反力的消失，隧道有一定的抬升. 而且垂直顶升施工阶段影响范围主要是隧道开口环以及开口环外三环相邻标准环.

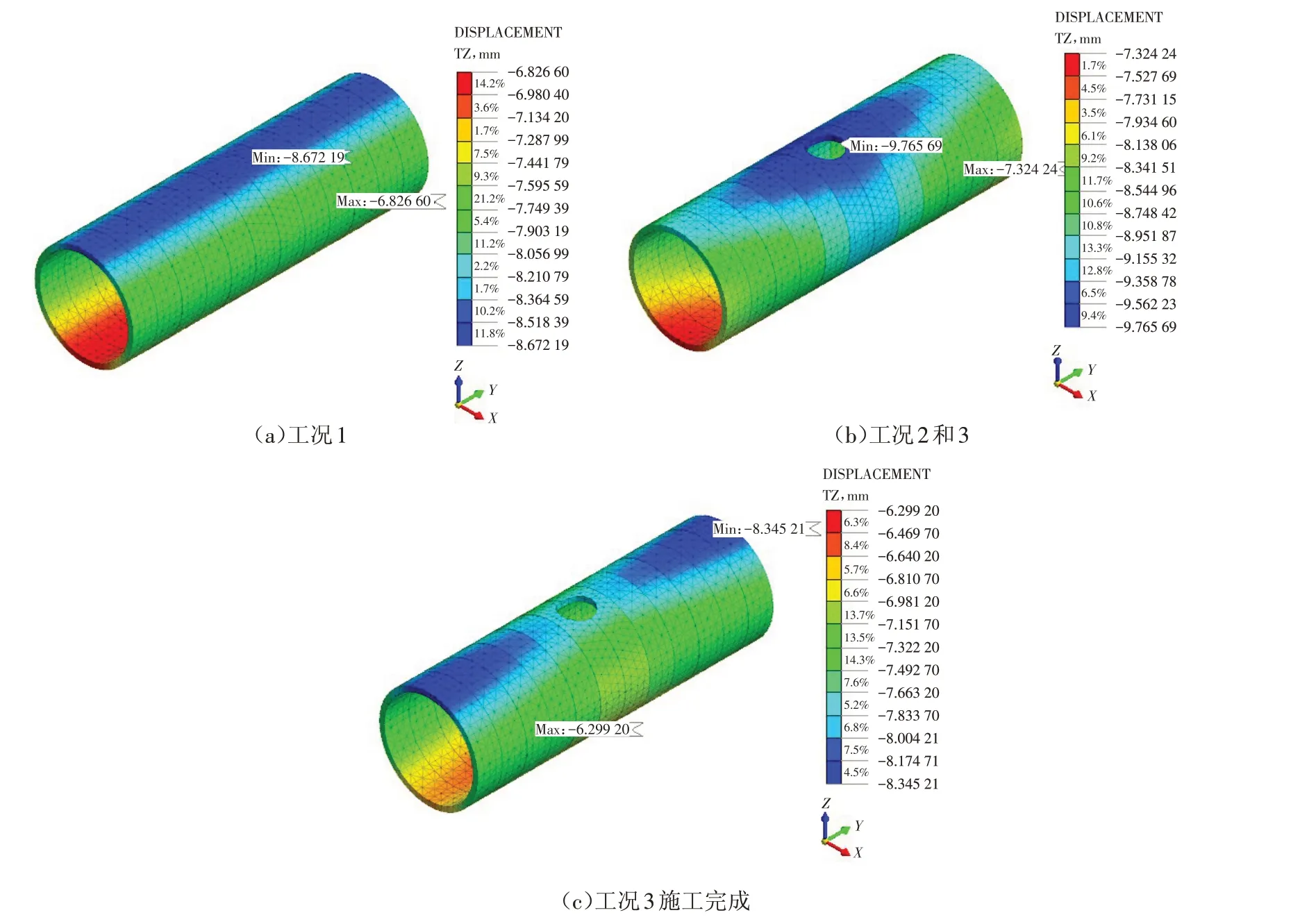
图6 不同工况下隧道竖向位移云图Fig.6 Vertical displacements of tunnel of different working conditions

由表4可以看出，开口环与相邻环在垂直顶升施工阶段的椭圆度（ΔD/D）变化规律一致，具体为从工况1 进入到工况2，椭圆度减小，从工况2进入到工况3，椭圆度增大. 如开口环的椭圆度在工况1 时为0.25‰，在工况2 时为0.1‰，工况3 时为0.206‰.开口环椭圆度在工况2 时较工况1 时减小了0.15‰；在工况3 时较工况2 时增加了0.106‰. 可见，垂直顶升前期开口环和相邻环收敛变形，垂直顶升后期，开口环和相邻环呈扩张趋势. 同时可看出，开口环的椭圆度变形比相邻环的大.

提取隧道底部竖向位移结果分析，来考察不同工况隧道底部管片变形规律，如图7为不同工况下隧道底部竖向位移值. 可见，隧道底部竖向位移变形规律与图6 的云图揭示的规律一致，最大沉降值为工况2 的9.02 mm，较工况1 的6.84 mm 增加了2.18 mm，大于顶部沉降增加值1.09 mm，说明隧道衬砌结构响应规律，从底部向上发展扩散，并逐渐衰减. 所以底部影响最大，顶部逐渐减弱. 而工况3与工况2相比，隧道底部有一定的抬升. 沉降和抬升的主要影响范围均是开口环及相邻三环. 工况2下，因顶升反力的作用，隧道底部管片变形呈中间大，两端小的不均匀沉降规律，最大沉降值发生在开口环底部.

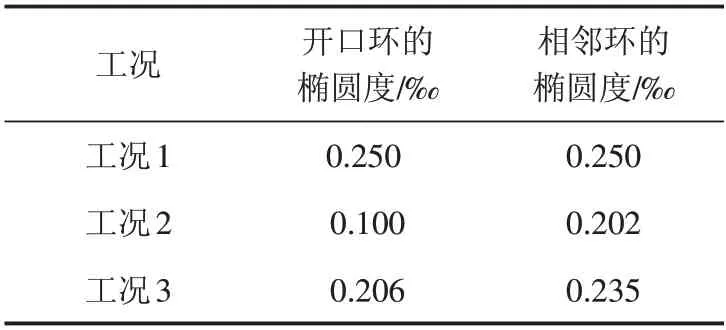
表4 不同工况下隧道环椭圆度Tab.4 Ellipticities of tunnel of different working conditions

为得到开口环与相邻环的变形结果，布置位移测点如图8所示. 为了得到垂直顶升施工引起的位移，提取的数据是基于工况1的增量变形. 如图9所示（图中变形值为正表示向圆环内变形），开口环及相邻环上相应测点的位移均呈现先增大后减小的规律，垂直顶升引起的管片竖向位移显著大于横向位移，开口环变形大于相邻环.

图7 隧道底部管片竖向位移Fig.7 Vertical displacements at the bottom of the tunnel

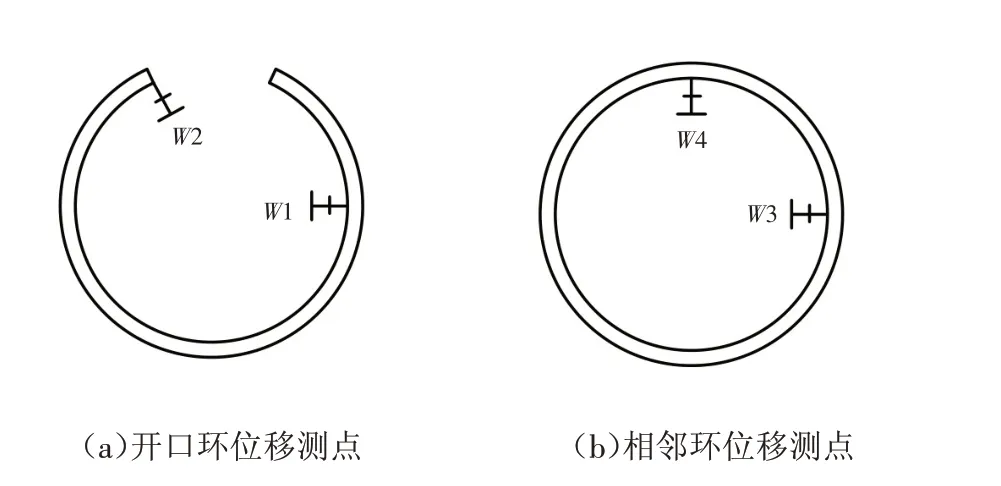
图8 管片位移测点布置图Fig.8 Layout of the displacement monitoring point

图9 基于工况1开口环与相邻环测点的位移变化Fig.9 Displacements of monitoring points of open ring and adjacent ring based on working condition 1

3.2 模型合理性验证

本文用工况2下的理论计算来验证数值模拟结果的合理性. 理论计算主要以Winkler弹性地基梁［14-15］和志波由纪夫提出的竖向等效连续化模型为基础［16-17］. 现将理论成果介绍如下.

将隧道纵向看作是Winkler弹性地基无限长梁，工况2下顶升反力以均布线荷载q（ x ）形式作用于隧道结构，以顶升反力中心为原点，隧道纵向为x轴，建立计算模型如图10所示. 引入地基沉降与基础梁的挠曲变形协调方程［18］，可得隧道与地层相互作用的力学方程为：

式中：EI 是隧道刚度；S（ x ）是隧道竖向位移；K是地基基床系数k 与隧道外径D 的乘积；q（ x）是作用在隧道上的顶升反力分布线荷载.

对于分布线荷载q（ x ）作用下的隧道，取一点ξ ，作用的集中荷载为q（ ξ ）d ξ，该荷载引起隧道上任意点x的位移dS（ x ）为：

式中：kb为单个接头螺栓的平均线刚度，kb=EbAb/lb，Eb为螺栓弹性模量；Ab为螺栓面积；lb为螺栓长度；ls为环宽；Ac为隧道管片环截面积；n为纵向螺栓个数，具体值如表2所示. 将表2的参数，代入式（6），可以算得中性轴位置的角度ψ=1.033，代入式（5）可算得完整连续隧道等效刚度（ EI）eq=3.684×107kN·m2，隧道刚度EI =0.8（ EI）eq=2.947 2×107kN·m2，基床系数k=10 000 kN/m3，隧道外径D=6.0 m，算得λ=0.162. 工况2 下均布荷载q=300×2=600 kN/m，a=-1，b=-1. 将上述参数代入式（4），计算得到工况2顶升反力作用下隧道纵向竖向位移理论值，与数值模拟结果进行对比.

图11 为工况2 顶升反力荷载诱发盾构隧道变形的理论计算结果和有限元计算结果对比图. 由图可以看出，理论主要沉降范围略小于有限元计算结果，但整体而言理论计算结果与有限元结果曲线均为接近正态分布曲线，曲线总体变化趋势相同. 理论计算得到的最大沉降位移值为1.96 mm，与数值计算结果2.15 mm 相比，误差约为8.7%，小于10%，满足精确度要求. 由此说明，模型具备一定的合理性.

图11 理论与数值计算位移结果对比Fig.11 Comparison of theoretical results and numerical results

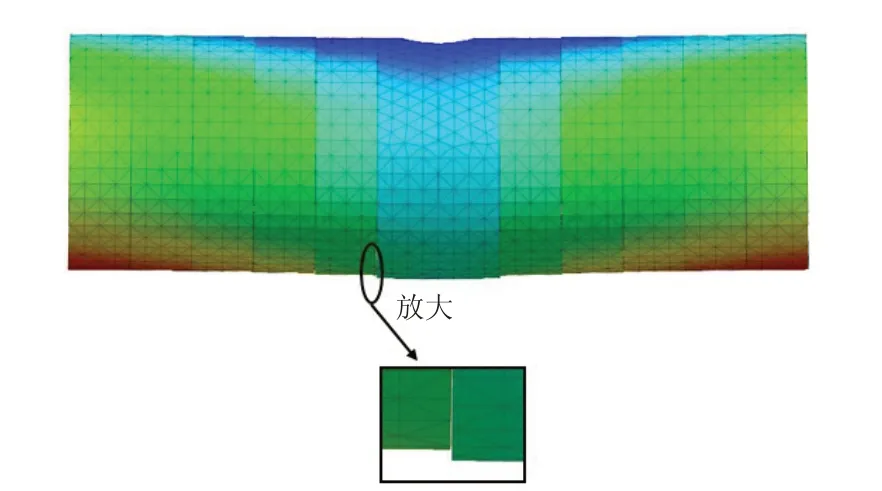
图12 工况1隧道整体竖向变形计算云图Fig.12 Vertical displacement distributions of tunnel of working condition 1

3.3 接头变形分析

图12给出了隧道整体竖向变形计算云图. 可见，受到垂直顶升的影响，隧道发生比较明显的错台和较小的张开，由于错台相对于张开更为明显，因此在分析中主要考虑接头的环缝错台的影响. 工况1下隧道不产生环缝错台，所以主要考虑工况2和工况3下隧道环缝错台的变化规律.

工况2、工况3下隧道不同位置的错台沿隧道纵向的分布曲线见图13. 图13（a）给出了不同工况下隧道底部错台和顶部错台沿隧道纵向的分布曲线. 可知，隧道底部错台和顶部错台沿隧道纵向呈对称分布，隧道中间接头错台接近0，隧道两侧错台均呈先增大后减小的规律. 最大错台发生在工况1开口环与相邻环之间的隧道底部位置，达到0.54 mm，而顶部最大错台发生在工况2开口环与相邻环之间，为0.1 mm. 图13（b）给出了隧道腰部错台沿隧道纵向的分布，可以看出侧向错台的分布规律与顶部错台、底部错台相似，最大错台同样发生在工况1开口环与相邻环之间. 相比于顶部接头、底部接头单一的竖向错台，腰部接头则在竖向和侧向2个方向发生错台，错台量最大值分别为0.21 mm和0.26 mm，此时腰部的总错台量约为0.33 mm，大于顶部最大错台量0.1 mm而小于底部最大错台量0.54 mm. 因此沿隧道纵向，开口环与相邻环之间断面的错台量最大，在该断面中，最大错台量大小关系为：底部错台＞腰部错台＞顶部错台. 底部错台为该断面中变形最大的，是影响隧道防水失效的重要因素.

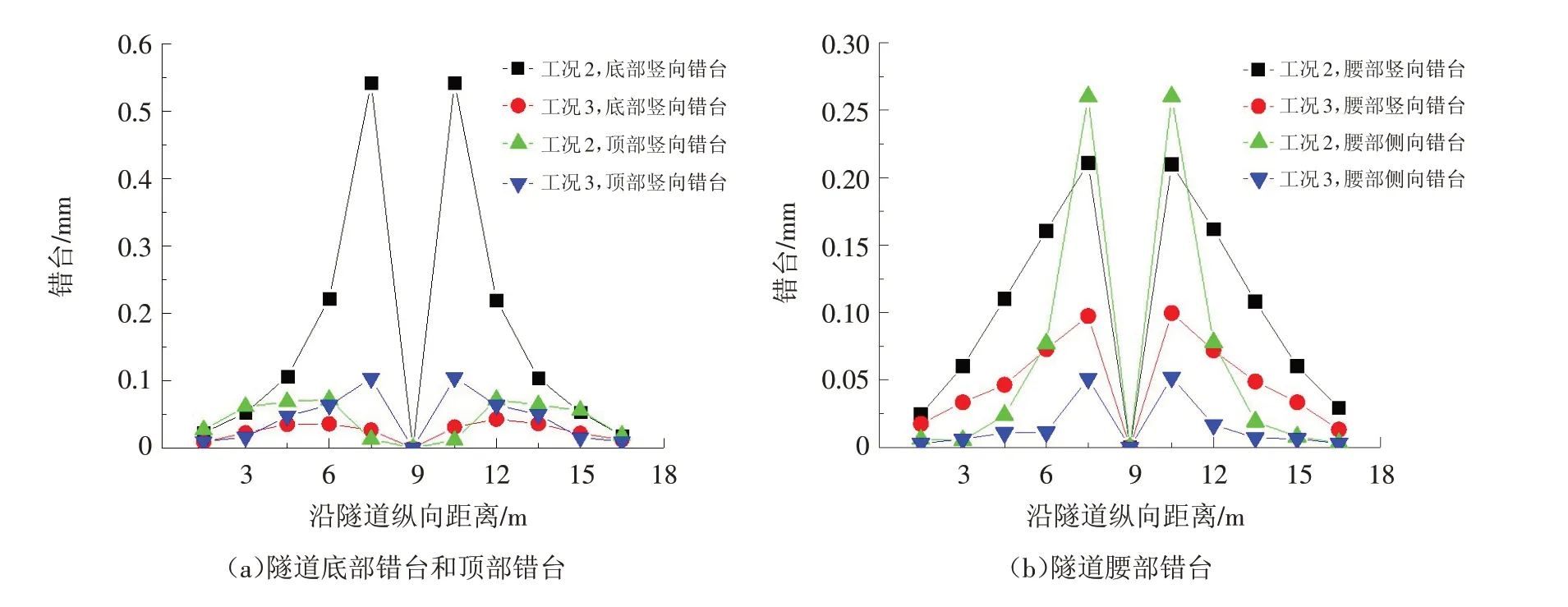
图13 不同工况下隧道错台沿纵向分布曲线Fig.13 Distribution curves of tunnel dislocations along longitudinal direction

4 顶升反力敏感性分析

由于隧道埋深、建设条件不同，垂直顶升所需的顶升力也不尽相同，而顶升力直接决定了隧道结构的力学响应程度，为此开展不同顶升力作用引起的盾构隧道和接头变形的规律分析. 现在现有模型基础上改变顶升反力大小，分别取240 t和360 t.

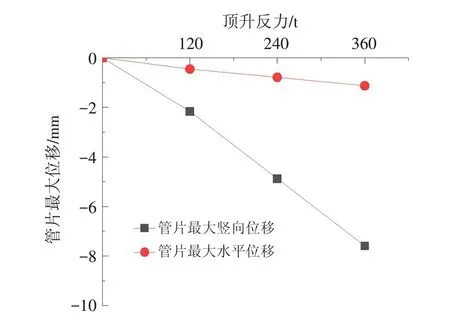
图14 不同顶升反力对应的管片最大位移曲线Fig.14 Maximum displacement curves of segments under different jacking reaction forces

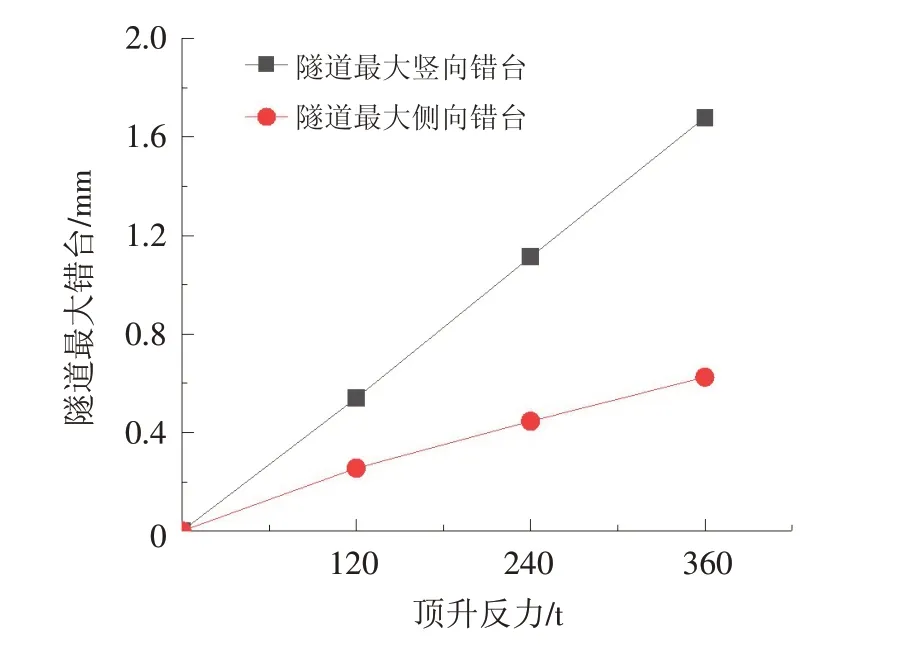
图15 不同顶升反力对应的管片最大错台曲线Fig.15 Maximum dislocation curves of segments under different jacking reaction forces

图14～图15为不同顶升反力对应垂直顶升施工引起的管片位移和接头变形情况. 由图可知：①垂直顶升施工引起的管片最大竖向位移和水平位移的差值、隧道最大竖向错台和侧向错台的差值均随着顶升反力的增大而愈发的明显；②垂直顶升施工引起的管片最大竖向位移、水平位移、隧道最大竖向错台、侧向错台均随着顶升反力的增大而近似线性增大.

5 结论

通过数值计算，分析盾构隧道内竖井垂直顶升施工引起的管片和环缝接头变形规律，并以理论计算验证数值模型具备一定的合理性，主要得到如下认识.

1）垂直顶升施工对管片变形的影响主要集中在开口环以及相邻三环标准环，对开口环管片变形的影响大于相邻环，对隧道底部的影响大于隧道顶部，竖向变形大于横向变形.

2）垂直顶升前期隧道整体下降，开口环和相邻环收敛，拱顶和拱底下沉，隧道底部最大沉降值发生在开口环底部. 垂直顶升后期，顶升反力减小，隧道整体有一定的抬升，开口环和相邻环扩张.

3）垂直顶升施工阶段，隧道的环缝接头变形呈以错台为主，伴随着少量张开的特点，其中开口环与相邻环之间的错台量最大，且在底部竖向错台最明显.

4）垂直顶升施工引起的隧道最大竖向位移与水平位移、最大错台量均随顶升反力的增大而同向近似线性增大，其中最大竖向位移和水平位移的差值、隧道最大竖向错台和侧向错台的差值均随顶升反力的增大而愈发的明显.