模糊时间窗下生鲜食材配送路径优化

王莉 张智勇 舒国云

摘 要：以“互联网+食材”B2C配送模式为研究对象，针对该模式下冷链企业存在的高配送成本与低客户满意度矛盾，本文在配送路径规划中引入模糊时间窗限制，设计B2C生鲜食材配送线路优化模型，提升to C配送服务水平。基于粒子群算法设计随机键编码和解码方式，并通过案例计算验证，为相关企业提出最优配送路径规划方案与建议。

关键词：生鲜食材B2C;模糊时间窗;客户满意度;路径优化;PSO

当前“互联网+食材”的B2C生鲜食材配送模式成为一二线城市的主流趋势，为满足消费需求，诞生了如美菜、链农、每日优鲜等供应企业，提供高质量的生鲜产品的线上订单、线下配送服务。B2C模式以客户需求为导向，冷链企业通过采购、仓储、城市配送等满足客户需求。一方面，对于像果蔬类季节性收获的生鲜产品，企业需通过冷藏仓储满足客户各时间窗需求;另一方面，客户消费行为具有时效性强和服务质量高的特点，需要通过城市配送中心周转调拨满足需求。在此背景下，生鲜食材配送企业面临巨大的成本压力和客户满意度考核，因此计算最优冷链配送路径是提升企业核心竞争力的有效方案。

一、文献综述

针对冷链最优路径的问题，传统的研究方法以成本最小为目标构建数学模型，如张文峰（2017）考虑果蔬冷链配送相关的建设费用和运输成本，设计双目标模型为选择最佳的配送路径提出科学建议。随着冷链配送研究的不断深入，学者们在模型中引入更多实际影响因素，王智忆等（2017）在研究中考虑车型、配送温度、载重限制等因素对路径优化的影响。姚源果等（2019）探讨了在途时间对配送的影响，提出在网络中设置接驳点求解最优路径规划。

VRPTW的学术研究从标准VRP问题的基础上拓展而来，在发展初期主要集中在旅行商问题的应用研究。J.Brito对软旅行时间窗进行了探讨，提出将时间约束转变为成本函数的方法。Xiangyong Li从时间随机性切入，对受时间窗限制的配送路径优化问题进行了深度研究。在冷链配送领域，李军涛（2019）对在模糊时间窗约束下的生鲜冷链配送路径优化复杂问题进行了探讨，提出考虑时间约束能有效提升配送服务水平并降低物流成本。生鲜产品具有易腐易损的物理特征，配送任务具有很强的时效性，研究其时间窗限制下的路径优化问题具有很强的现实意义。

就VRPTW问题的求解，张文博（2016）提出两阶段规划测量方法，在前段采用遗传算法求解，后段使用模拟退火算法优化结果，得出时间窗限制下的车辆路径最优解。Chengming Qi对多蚁群算法进行改进，提出将蚁群算法与随机算法组合。Xia Y等将所需车辆数量的最小化作为主要目标，改进禁忌搜索法进行求解开放式车辆路径问题。

综上所述，时间窗设置能更加真实地反映实际配送问题，尤其针对生鲜食材冷链配送，引入时间窗约束可更好地起到降本增效的作用。结合配送时效和客户收货时间要求，本文引入模糊时间窗限制，建立包含企业冷链成本和客户满意度的双目标模型，并设计粒子群算法，研究模糊时间窗限制条件下的生鲜食材冷链配送路径最优解。

二、问题描述及条件假设

1.问题描述

B2C生鲜食材配送企业拥有一个多配送中心冷链网络，满足不同位置客户的配送服务，客户位置和需求量为订单信息。企业运营成本考虑冷藏车的使用成本，运输、制冷产生的成本和能耗，食材损坏造成的货损成本，设计惩罚成本函数计算客户满意度成本，求解最低企业运营成本和最高客户满意度条件下的最优配送路径。

2.条件假设

（1）各配送中心冷藏车型号与额定载重相同;

（2）各配送路线的客户订单总和小于冷藏车额定载重;

（3）一个客户点的订单量只能被一辆冷藏车一次性满足;

（4）各配送中心库存充足，无缺货的情况;

（5）各冷藏车出发和返回地点为同一配送中心;

（6）网络中配送路线总数小于车辆总数;

（7）生鲜食材腐坏程度仅与运输时间及在客户点的服务时间相关。

三、模型构建

1.符号说明

参数符号：

l：配送中心;Kl：冷藏车;额定载重;qi：客户点i的订单量;p：货物价格;c：运输单位距离成本;w1：运输过程货损系数;w2：车门开闭操作期间货损系数;ω：冷藏车单位时间能耗量;η：冷藏车在客户点的能耗占比;λ1：惩罚冷藏车提前送货的单位成本;λ2：惩罚冷藏车耽误送货的单位成本。

决策变量：

2.模型构建

（1）固定成本

企业使用冷藏车配送需支付的固定费用，设单台车辆固定成本为，企业固定成本记为C1：

（2）运输成本

本文假设冷藏車运输成本为与行驶距离相关的线性函数，记为C2：

（3）货损成本

生鲜食材的货损成本包括在途货损和因卸货开闭车门引起的货损，货损成本记为C3：

（4）能耗成本

能源消耗成本与行驶时间和客户需求量有关，冷藏车能耗成本记为C4：

（5）惩罚成本

企业未在客户期望的收货时间区域到达就会产生惩罚成本，记为C5：

综上所述，将配送总成本最小化记为MinZ：

由此可得：

（6）客户满意度函数

通过计算车辆到达时间与客户点期望收货时间窗的偏差程度来量化客户满意度，本文利用隶属度函数定义客户点i的满意度G（Si）：

在（8）中，[0，EETi]、[ELTi，+∞]分别代表早到与迟到2种情况，客户在这2个时段内不接受服务，满意度为0;[ETi，LTi]是客户满意度最高的收货时段，满意度为100%;[EETi，ETi]、[LTi，ELTi]为客户满意度极值两侧能接受的收货时段，Ai与ETi、LTi的偏离程度越大，满意度值越小。

客户满意度函数为：

本文模型与约束条件如下：

（12）表示配送路径总数小于冷藏车总数;（13）表示冷藏车从所属配送中心驶出必须驶回;（14）和（15）表示要满足全部客户点需求，且各客户点要一次性满足;（16）表示各配送线路的总订单量小于冷藏车额定载重;（17）表示同一配送路径内，冷藏车不能从一个配送中心行驶到另一个配送中心;（18）表示冷藏车到达时间;（19）表示模糊时间窗下服务时间约束。

本文从冷链企业运营角度出发，将最小化的配送总成本设为主目标，客户的满意度函数当作次要目标，设定最大的满意度定值，最后得到模糊时间窗限制条件下生鲜食材冷链配送路径的单目标优化模型：

（20）为单目标模型函数。新增约束条件解释：（21）表示客户点对冷链车配送服务的时间满意度;其他约束条件同上。

四、模型求解思路及算法设计

1.求解思路

本文的配送路径问题属于NP-难题，采用整体法求解思路，化多配送中心为单配送中心求解，如图1所示：

整体法是将配送网络视为一个系统，所有车辆从“中心仓”出发，完成配送返回“中心仓”视作一次路径。具体求解过程如下：

（1）建立一个虚拟“中心仓”与各实际配送中心相连，形成一个仅由“中心仓”和配送中心组成的虚拟配送网络，各配送中心由“中心仓”提供服务。

（2）在虚拟网络中加入客户点，配送车辆从“中心仓”先经过一个实际配送中心再到客户点。配送车辆完成服务也需先返回实际配送中心再回“中心仓”才算完成一次送货。

“中心仓”为一个理想点，与实际配送中心无运输距离和时间，因此不会影响模型计算结果。此外，客户点不是固定配置给某一配送中心，而是根据实际订单量分配。

2.粒子群算法设计

（1）编码解码过程

本文设计了基于随机密钥的编解码过程：

编码过程：假设客户点数量为N，冷藏车总数为K，则配送网络的编码维度为（N+K-1）*1，各维度取值范围为[0，1]。

解码过程：采用随机键解码方法，最小值对应1，次小值对应2，依次类推可将原本（N+K-1）*1维属于[0，1]的小数，转换形成一个1-（N+K-1）的序列，1-N代表客户点，N+1-N+K-1代表路线分割符号对路径进行划分，得到配送网络的路径规划。

（2）算例说明

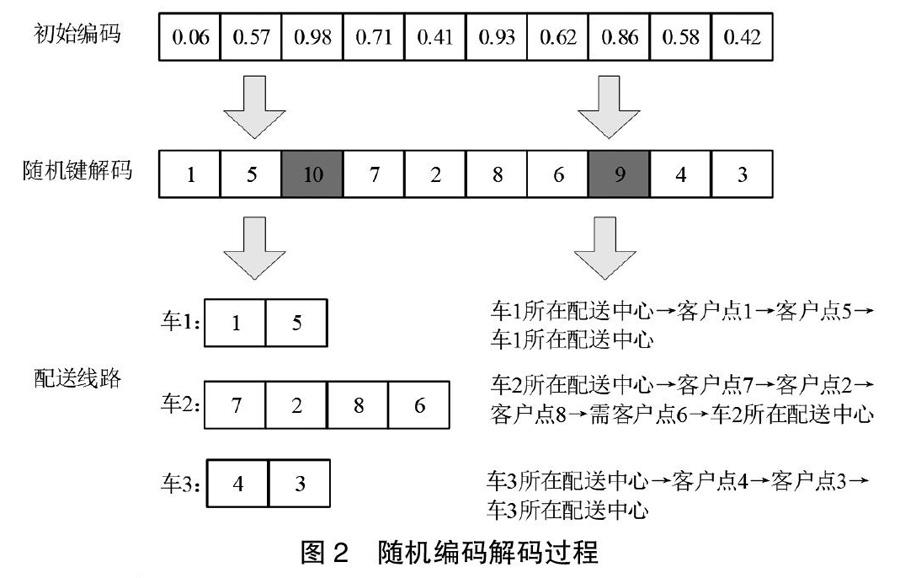
假设N=8，K=3，则（N+K-1）*1=10。利用随机键解码方法，将原本的小数编码（0.06，0.57，0.98，0.71，0.41，0.93，0.62，0.86，0.58，0.42）转换为（1，5，10，7，2，8，6，9，4，3）序列，1-8代表客户点，9和10代表路线分割符号，形成三条配送路线。如图2所示：

五、算例验证及结果分析

1.算例验证

A公司主营有机绿色农产品食材，为了保证食材质量，其产品的预冷、加工、储存和配送均保持低温环境。同时，为保证服务满意度，与客户签订配送收货时间窗协议。公司通过三个配送冷库满足分布在深圳各地的26处客户需求。相关数据见下表：

2.结果分析

本文采用主要目标法处理多目标函数问题，先根据A公司的配送数据确定最佳客户满意度值，作为满意度函数释放的界限值，再将其代入约束条件求解最优配送路径。

（1）最佳客户满意度值

利用matlab编码计算，粒子群计算的相关参数设定如下：种群规模=60;惯性权重ω=1;权重系数r1=0.9，r2=0.99;学习参数c1=1.5，c2=2;终止代数=500。运行程序，设置最优的客户满意度分别为：80%、85%、90%、95%，多次重复运行，最终取得10次较优解和对应配送成本比较：

从表5和图3结果，A公司的配送总成本在同一水平的满意度背景下大致相同，这与实际情况相符，也验证了本文设计的粒子群优化算法的有效性。客户点满意度在80%至90%区间时，随着满意度水平提高，配送总成本也随之小幅上升，但当客户的满意度水平从90%提升到95%时，配送总成本出现大幅增加。因此，本文将90%作为最佳客户满意度值，代入模型求解最优路径。

（2）配送路径求解

在客户满意度设定为90%的情况下，经过多次运行结果分析，得出配送成本最小值为9106元，共使用9辆冷藏车，具体配送路径如图4所示：

车辆路径规划方案如下：

路径1：27-9-27;

路徑2：27-17-12-27;

路径3：27-1-14-27;

路径4：28-13-7-26-28;

路径5：28-4-15-24-28;

路径6：28-2-20-3-28;

路径7：29-8-25-18-19-29;

路径8：29-22-6-11-10-29;

路径9：29-21-23-16-5-29。

六、结论

本文主要研究工作和结果如下：

1.本文构建了模糊时间窗限制条件下，以配送总成本最小和客户满意度最高的双目标冷链配送路径优化模型，可为企业计算出最优的配送网络路径安排方案，不仅保持最佳的客户满意度，还达到最小的配送总成本。

2.本文采用整体法的思路对模型进行求解，并结合实际案例设计粒子群优化算法计算最佳配送方案，不仅验证了研究的有效性，还为模糊时间窗限制下的冷链路径优化方案提供了一个量化的理论支持。

生鲜食材由于自身特殊的易腐易损特征，其冷链配送具有严格的时效性。考虑模糊时间窗约束下生鲜食材的配送，不仅能有效保证对客户满意度，还能反向催化配送品质的提升。针对生鲜食材冷链配送企业发展，本文最终提出：在面对最小化配送总成本和最大化客户服务水平两个发展目标时，企业无需一味追求实现两者最大化，而应选择一个满意度水平的临界值作为企业的最优服务水平。这样一方面可以保证较高的客户服务质量，另一方面也不会增加过高的配送成本，达到两者平衡。

参考文献：

[1]張文峰，梁开豪.生鲜农产品冷链物流网络节点和配送的优化[J].系统工程，2017：119-123.

[2]王智忆，陆敬筠.考虑低碳的冷链物流车辆配送路径优化[J].科技管理研究，2017，37（17）：228-232.

[3]姚源果，贺盛瑜.基于交通大数据的农产品冷链物流配送路径优化研究[J].管理评论，2019，31（04）：240-253.

[4]Brito J，Martinez F J， Moreno J A， et al. Fuzzy optimization for distribution of frozen food with imprecise times[J].Fuzzy Optimization & Decision Making，2012，11（3）：337-349.

[5]Xiangyong Li， Peng Tian， Stephen C.H.Leung. Vehicle routing problems with time windows and stochastic travel and service times： Models and algorithm[J].International Journal of Production Economics，2010，125（1）：137-145.

[6]李军涛，路梦梦，李都林，刘朋飞.模糊时间窗多目标冷链物流路径规划[J].中国农业大学学报，2019，24（12）：128-135.

[7]张文博，苏秦，程光路.基于动态需求的带时间窗的车辆路径问题[J].工业工程与管理，2016，21（06）：68-74.

[8]Chengming Qi， Yunchuang Sun. An Improved Ant Colony Algorithm for VRPTW[J]. International Conference on Computer Science and Software Engineering，2009：455-458.

[9]Xia Y， Fu Z. Improved tabu search algorithm for the open vehicle routing problem with soft time windows and satisfaction rate[J].Cluster Computing，2018，1（2）：1-9.

作者简介：王莉（1997- ），女，汉族，四川达州人，硕士研究生，华南理工大学经济与贸易学院，研究方向：冷链物流、智能优化;张智勇（1979- ），男，汉族，湖北浠水人，华南理工大学经济与贸易学院，教授，博士生导师，研究方向：供应链管理、决策理论;舒国云（1975- ），女，汉族，贵州贵阳人，华南理工大学经济与贸易学院实验员，研究方向：供应链管理与应用