厘清算理，提高运算能力

袁玉玲

《义务教育数学课程标准（2011年版）》指出：运算能力主要是指能够根据法则和运算律正确进行运算的能力。培养运算能力有助于学生理解运算的算理，寻求合理简洁的运算途径解决问题。本期，我们从算理与算法的关系、运算素养的培养等视角，探讨如何培养学生的运算能力。

数学运算能力是学生需要掌握的基本能力，如何提高学生的运算能力呢？笔者以北师大版三年级上册《蚂蚁做操》所解决的两、三位数乘一位数（不进位）的计算为例，谈谈如何以教学内容为载体，以探究算理、算法为抓手，促进学生正确、合理、灵活地进行运算，提高运算能力。

一、数形结合，感知算理与算法

哲学家康德认为，无论一种知识以什么方式以及通过什么手段与对象发生关系，它与对象直接发生关系所凭借的以及用一切思维当作手段所追求的，就是直观。直观教学在小学数学运算能力培养中具有重要作用。

师：如下图，蚂蚁排着整齐的队形正在做操，你能从图中发现哪些数学信息？

生1：每行有12只蚂蚁，有4行。

师：你还想从中知道些什么呢？

生2：我想知道一共有多少只蚂蚁。

师：请在草稿本上列出算式，并想一想为什么这样列。

生3：我列的算式是12×4，应该理解为4个12或12个4。

师：你准备怎样计算？能想到哪些方法？

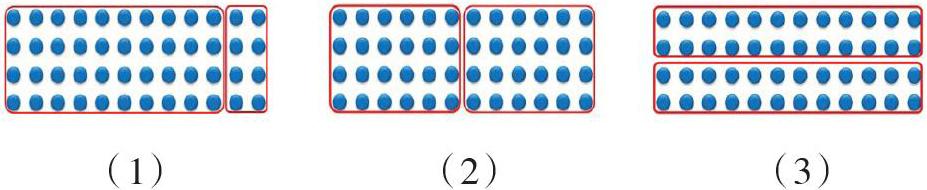
计算以全开放的状态开展，学生先后采用了口算法、列表法、圈实物图法、画点子图法。当学生说：“我用的是点子图”，笔者立刻追问：“你打算将点子怎样排列？为什么这样排列？”学生打算每行12个，排成4行，因为这样排列，和蚂蚁做操的队形一样。紧接着，笔者话锋一转：“大家就利用点子图来圈一圈吧，看看你又能想到哪些不同方法呢？”在反馈环节中，学生先后用到了拆数法中的“破十法”，每行12个拆为10和2[如图（1）];平均分法，即每行12个平均分成2份或者每列2个平均分成2份[如图（2）、图（3）]。

笔者通过三个层级的数形结合，使学生从中感知算理与算法。第一层级：实物图直观模型呈现。学生通过直观图构建“12×4”的乘法算式模型，计算时，学生借助圈实物图的方式来进行。第二层级：将实物图抽象为点子图直观模型。当学生分享到点子图时，一个即时追问，只为给学生留白，使学生主动从生活实物图中抽象出数学图形，此刻，笔者不是把点子图呈现在学生眼前，而是继续追问“你打算将点子怎样排列？为什么这样排列？”这样做不仅为学生搭建了思考与想象的平台，而且使学生合理抽象出点子图直观模型，带给学生运用一一对应的数学思想设计点子图行数和列数的时机。第三层级：圈点子图直观模型进行计算。学生借助“圈”这一操作，说清了算式中每一个数的来源和实际意义。整个过程让学生充分经历、体验了解决“数”的问题，“形”功不可没，从而形象、便捷地感知算理与算法。

二、比较内化，领悟算理与算法

教育家乌申斯基认为，比较是一切理解和思维的基础，我们正是通过比较来了解世界上的一切的。在这节课中，“比较”遍及教学前、中、后各个阶段，以此帮助学生领悟算理与算法。

1.在直观模型中比较

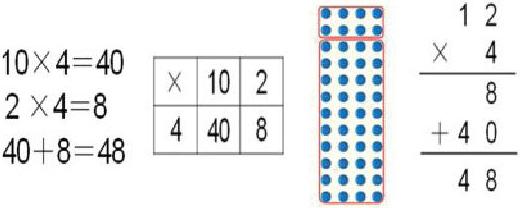
学生利用点子图直观模型，通过破十法和平均分法得到了以下三种算法：10×4=40，2×4=8，40+8=48;6×4=24，24×2=48;12×2=24，24×2=48。笔者没有就此止步，而是接着问：“请仔细观察图中这几种圈法和算式，你能从中发现什么？”学生借助图和式的比较得到，无论是破十法，还是平均分法，從形的视角来看，它们都是化一个整体为几个部分;从数的角度来说，都是化大为小。停顿片刻， 笔者继续问：“在这几种分法中，你更喜欢哪一种？为什么？”学生认为，用拆数法把12拆成10和2更为简单，笔者紧追不舍：“简单在哪儿？”学生认为，10是一个整十数，10×4的得数40也是整十数，这样非常好算。学生通过所圈图形经历说理、列式、计算、比较等过程，对两位数乘一位数的算理和算法有了初步感知，为探究竖式计算法设下伏笔。

2.在竖式探究中比较

师：12×4你们列出了竖式的起始部分，接下来怎样计算呢？

生1：先用4乘个位上的2得8， 8要写在个位上。

师：为什么写在个位？

生2：因为2表示2个一，4表示4个一，它们相乘得8个一。

师：下一步该算什么？

生3：4乘十位上的1得4，因为这里的1表示1个十，所以得数是40，4写在十位，0写在个位，和8对齐， 40写在8的下面，再把积相加。

师：为什么把两次的积相加？

生4：因为把乘数12拆成了10和2两部分，乘数4只与个位上的2相乘后没有算完，还要与十位上的1相乘，最后再把这两部分积相加。

在这一环节中，教师只是一个引导者，学生不仅知道了怎样算、怎样写，而且把为什么这样算、这样写说得一清二楚，这和以前将数位与计数单位的比较密不可分，和本节课中对数形结合、圈图方法的比较息息相关。

3.在多种算法中比较

学生一共分享了4种计算方法，笔者以学生分享的先后顺序集中展示，如下图从左至右所示。

然后，笔者将“你能从这些算法中领悟到什么？”这个问题抛给学生。在反馈过程中，学生领悟到这4种方法虽然呈现形式不同，计算顺序不同，口算法、列表法、点子图法，都是从高位算起，而竖式法是从低位算起，但彼此之间的计算道理和方法相同。

借此比较之机，笔者以新学的竖式计算为中心，重排顺序，师生共画思维导图，如下图所示。

上述思维导图不仅使学生借助其他方法厘清了竖式法中每一步的算理与算法，而且通过追问“以后计算时，你可能会首选什么方法？为什么？”引导学生再次比较各种方法，将运算思维向更抽象、更简洁的台阶迈进，使新旧知识、数学思想与方法形成有效对接。历经三轮比较，使学生对算理与算法有了更深刻的领悟。

三、类比迁移，根植算理与算法

数学家开普勒曾指出：“我重视类比胜过任何别的东西，它是我最信赖的老师，它能揭示自然界的秘密。”在整个课堂里，笔者共为学生创造了三次类比解决问题的时机。

1.第一次类比：你心目中乘法竖式的模样

“怎样算12×4？你还有其他不同的方法吗？”个别学生在最后提到了竖式法，笔者问学生怎么想到的，学生认为加减法都有竖式法，猜想乘法是不是也可以用竖式法来计算。笔者即刻统计哪些学生听说过或者见到过。接下来笔者说：“没见过的同学想一想，你心目中的乘法竖式是什么样？在草稿纸上试着写一写，见过的同学请把这个竖式在草稿本上写下来。”同时，请一名没见过的学生板演，他写出了竖式中的起始抄题部分，笔者问他为什么这样写，学生说：“我觉得和前面的加减法竖式一样，只是符号不同，这里是乘号。”通过这次类比，为学生托起了想象的翅膀。

2.第二次类比：为什么先从低位乘起

笔者设问：“在竖式计算过程中，我们刚才是先算的4乘2，后算的4乘10，为什么这样算？”学生回答：“如果先算了高位，算低位时会出现向高位进位或借位的情况，高位还要再算，这样很麻烦，所以从低位算起更简单。”通过与前期加减法竖式计算进行类比探究，学生都知道要从个位算起，部分学生知道从个位算起简单一些，少数学生知道从个位算起为什么简单。

3.第三次类比：三位数乘一位数

三位数乘一位数，首先让学生用自己喜欢的方法独立计算，然后分享时自然而然地类比迁移，说清楚每一步的意思。

三次类比，将算理与算法根植在学生心底，可谓水到渠成。

对于小学低年级学生来说，厘清算理与算法，并不是要求他们知道算理与算法概念的内涵，而是指教师在具体的运算教学过程中，要结合具体实例，运用数形结合、比较内化和类比迁移等数学思想与方法，让学生知道为什么要这样算以及如何算，厘清“为什么”以及“如何做”的关键性问题，才能扫除运算教学中存在的根本性问题，从而全面提高学生的数学运算能力。

（作者单位：宜昌市秭归县实验小学）

责任编辑 张敏