基于三阶段DEA模型的我国中医医院与中西医结合医院运行效率比较
2021-03-02李志广丁志远孔爱杰张婉莹
李志广,丁志远,孔爱杰,张婉莹
安徽中医药大学医药经济管理学院,安徽合肥,230012
近年来,随着医改的不断深入,中医类医院的功能定位进一步明确,国家对于中医药的扶持与管理力度也不断加大,政府把中医药发展上升为国家战略[1]。国务院印发的《中医药发展战略规划纲要(2016-2030年)》明确指出,中医药作为我国独特的卫生资源,在经济、科技、文化及生态领域中发挥着极其重要的作用。此外,在新冠肺炎的救治过程中,中医药全程参与且效果显著,在此次突发公共卫生事件中发挥了重要作用。作为中医医疗服务体系的主体,中医类医院的运营状况直接反映我国中医药卫生资源的配置效率。本文通过三阶段DEA法对2017年全国30个省(直辖市、自治区)中医医院和中西医结合医院运行效率进行测度,以期为我国中医药卫生资源合理配置和规划提供参考。
1 资料来源与方法
1.1 数据来源
研究数据来源于2017年《全国中医药统计摘编》、《中国卫生和计划生育统计年鉴》和《中国统计年鉴》。由于2017年《全国中医药统计摘编》数据显示西藏中医医院为0,中西医结合医院仅有1家,该样本不具有代表性,故本文的研究对象为我国除了西藏以外的其他30个省、直辖市、自治区的中医医院和中西医结合医院。
1.2 研究方法
数据包络分析模型由美国运筹学家Charnes、Cooper和Rhodes于1978年首次提出,随后Fried等学者于2002年在相关论文中提出了以DEA为基础的三阶段DEA模型[2]。该模型引入了随机前沿模型理论,剔除效率中管理无效率、环境因素和统计噪声的影响,从而获得更为准确且真实的效率状况[3]。本文采用三阶段DEA模型,分阶段研究中医医院和中西结合医院的医院运行效率。
1.3 指标选取
医院的运行效率是一个多投入、多产出的复杂系统,因此在利用DEA模型进行医院效率评价时,投入和产出指标的选取十分关键。不同的指标组合往往会导致结果的输出产生一定的差别,因此所选的投入产出指标需具有代表性、独立性、核心性等特征[4]。医院的运营投入主要涉及人力、物力和财力3个方面的资源,其中人力泛指职工数和卫生技术人员数,物力一般特指设备和固定资产,财力主要包括相关医疗成本、管理费用和业务支出等[5-7]。产出指标包括反映治疗效果的业务工作指标,如门急诊人次、住院人次、手术人次等,也包括反映医院收入的总收入等财务指标[8-10]。基于国内外文献分析以及指标的可获得性,本文选取机构数、实际床位数和卫生技术人员数作为投入指标,诊疗人次和出院人数作为产出指标。而三阶段DEA对于环境变量需要满足“分离假设”的要求,因此需选取对医院运行效率产生影响但又不可主观控制和改变的环境指标。通过文献回顾并结合数据的可获得性,本文最终选取城市人口密度、地区生产总值、总抚养比、病死率和中医机构财政拨款作为环境变量[11-15]。
2 结果
2.1 投入产出指标相关性分析
运用DEA模型时,需要进一步检验投入指标与产出指标之间的相关性,即两者是否能互相影响。从估计的相关系数结果来看,所有投入指标和产出指标的相关性均大于0.540,且在0.010水平上显著相关,说明投入产出具有较高的相关性,符合DEA模型对数据的同向性要求。
2.2 第一阶段,基于原始数据的BCC模型分析
利用传统DEA投入导向的BCC模型,结合DEAP 2.1软件,对30个省份中医医院和中西医结合医院的运行效率进行测度。表1显示,整体上我国中医医院的运行效率高于中西医结合医院,其综合技术效率均值分别为0.852和0.780。规模报酬方面,中医医院与中西医结合医院规模报酬不变的省份基本持平,但15个省份的中医医院出现规模报酬递减的现象,而中西医结合医院仅有4个省份。这说明我国中西医结合医院规模配置优于中医医院。
由于第一阶段是并未经过外部环境干扰因素滤除的初步DEA效率结果,所以并不能真实反映我国中医类医院实际的运营状况。因此,需要排除外部环境和随机干扰等因素,重新对综合技术效率进行测度与评价。
2.3 第二阶段,构建SFA回归模型对环境变量分析和投入变量的调整
使用Frontier 4.1软件,利用SFA回归对第一阶段松弛变量进行分解。松弛量是各省份的实际生产过程与效率最高情况下的投入之差,反映医院初始的管理无效率、环境变量以及随机误差值。SFA回归结果如表2所示。由于SFA是环境变量对投入松弛变量的回归,所以当回归系数为正时,环境变量的增加会带来相应投入松弛值的增加,原始投入越偏离投入目标值,从而使医院效率下降。反之,若回归系数为负,增加环境变量会减少投入变量松弛值,提高医院运行效率。
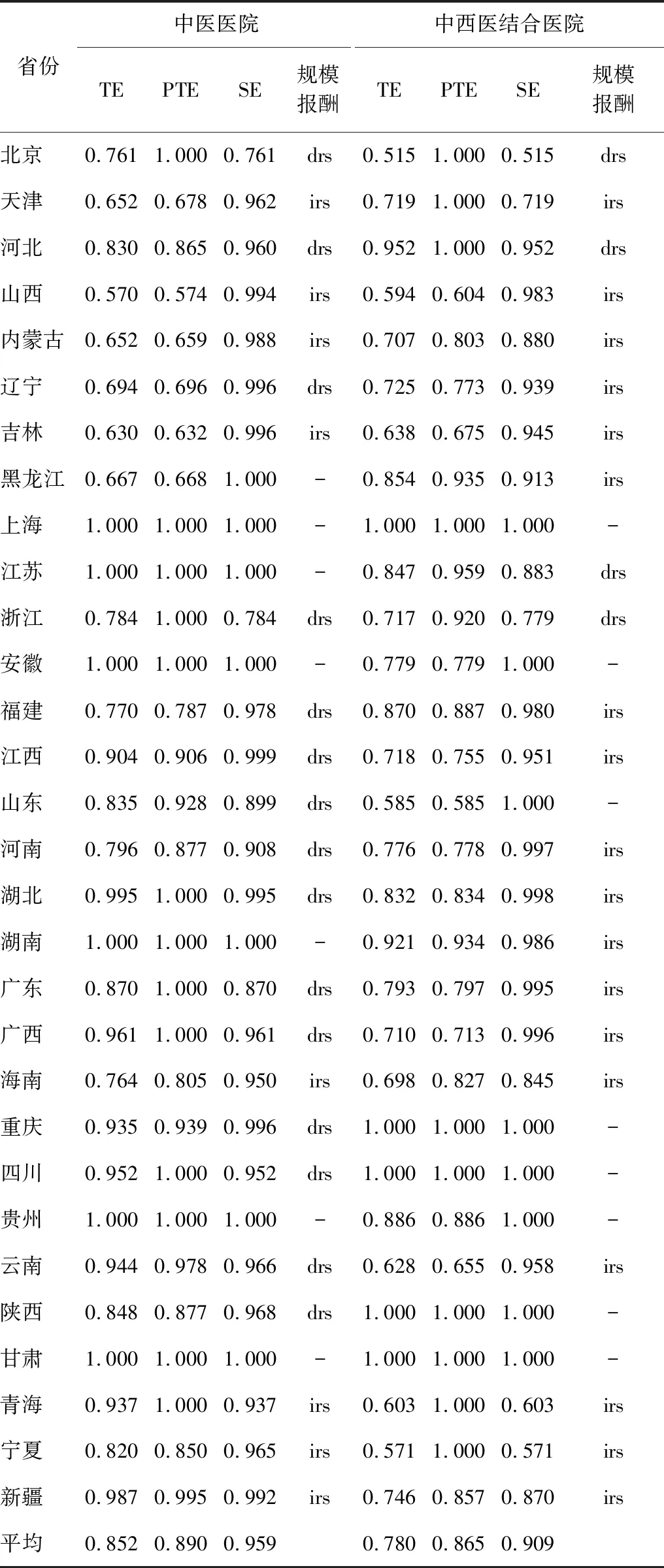
表1 我国中医医院与中西医结合医院传统DEA模型结果
结果显示,中医医院和中西医结合医院所有投入指标松弛变量的γ值均为1,说明两类医院经营管理因素对投入变量松弛值的影响占主导地位,而不是随机干扰。
中医医院。城市人口密度对3个投入变量的回归系数均为正值,且对机构数松弛值通过了1%显著性检验。说明随着城市人口密度的增加,将导致中医医院机构数、实际床位数和卫生技术人员数的投入冗余,降低医院运营效率。总抚养比和病死率对中医医院的机构数松弛值和实际床位数松弛值表现为负向显著,但与卫生技术人员松弛变量的回归系数为正。表明总抚养比和病死率可以约束中医医院的盲目扩张,优化设备资源的投入,但过度的中医药人员数投入,会造成投入冗余,导致医院人才使用效率下滑。地区生产总值对机构数松弛值和实际床位数松弛值呈现正向关系,而财政拨款却恰恰相反。同时,地区生产总值对卫生技术人员数松弛变量表现为负向抑制作用,但财政拨款却对卫生技术人员数松弛变量表现为正向促进作用。
中西医结合医院。回归结果显示,城市人口密度对机构数松弛变量和实际床位数松弛变量回归系数为正,且与机构数松弛变量通过1%显著性检验。然而城市人口密度对卫生技术人员松弛变量回归系数为负,与中医医院略有出入。地区生产总值的回归系数均为正,表明增加地区生产总值,会带来医院盲目扩张的风险,造成床位及卫生技术人员的浪费,导致运行效率降低。而总抚养比和病死率对3个投入变量松弛值表现为负向关系,即总抚养比和病死率的增加会减少资源浪费,提高医院的运行效率。进一步分析,财政拨款对机构数松弛值和卫生技术人员松弛值表现出正向关系,且与机构数松弛值通过1%显著性检验,但对实际床位数松弛变量回归系数为负。表明增加财政拨款有利于减少床位的浪费,但会造成医院数目的随意扩张和卫技人力资源的浪费。
2.4 第三阶段,基于调整后投入与产出数据的BCC模型分析
运用调整后的投入产出变量再次测算各省份的效率,此时的效率已经滤除环境因素和随机干扰的影响,是相对真实准确的。我国中医医院和中西医结合医院的综合技术效率、纯技术效率及规模效率分别为0.870、0.911、0.957和0.733、0.900、0.823。在滤除环境因素和随机干扰的影响后,与第1阶段结果相比,中医医院综合技术效率和纯技术效率均值上升,规模效率均值降低,而中西医结合医院的纯技术效率均值上升,综合技术效率和规模效率均值下降。说明我国现阶段两类医院的扩张规模速度同技术管理水平的发展步调不一致,导致综合技术效率出现差异。从整体上来看,我国中医医院的运营效率优于中西医结合医院,但两类医院的运行效率水平还有进步空间,资源配置仍需进一步优化。见图1。
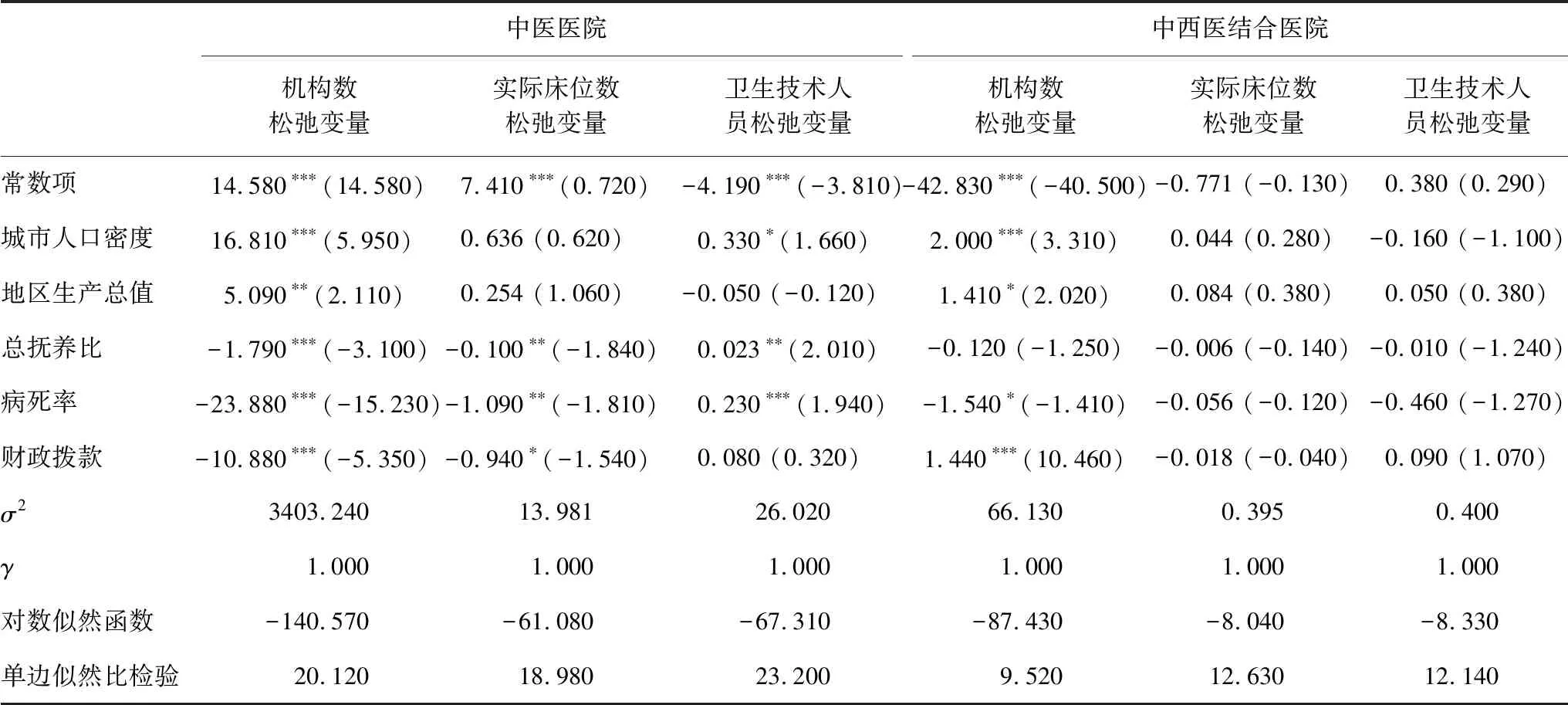
表2 SFA模型回归分析结果
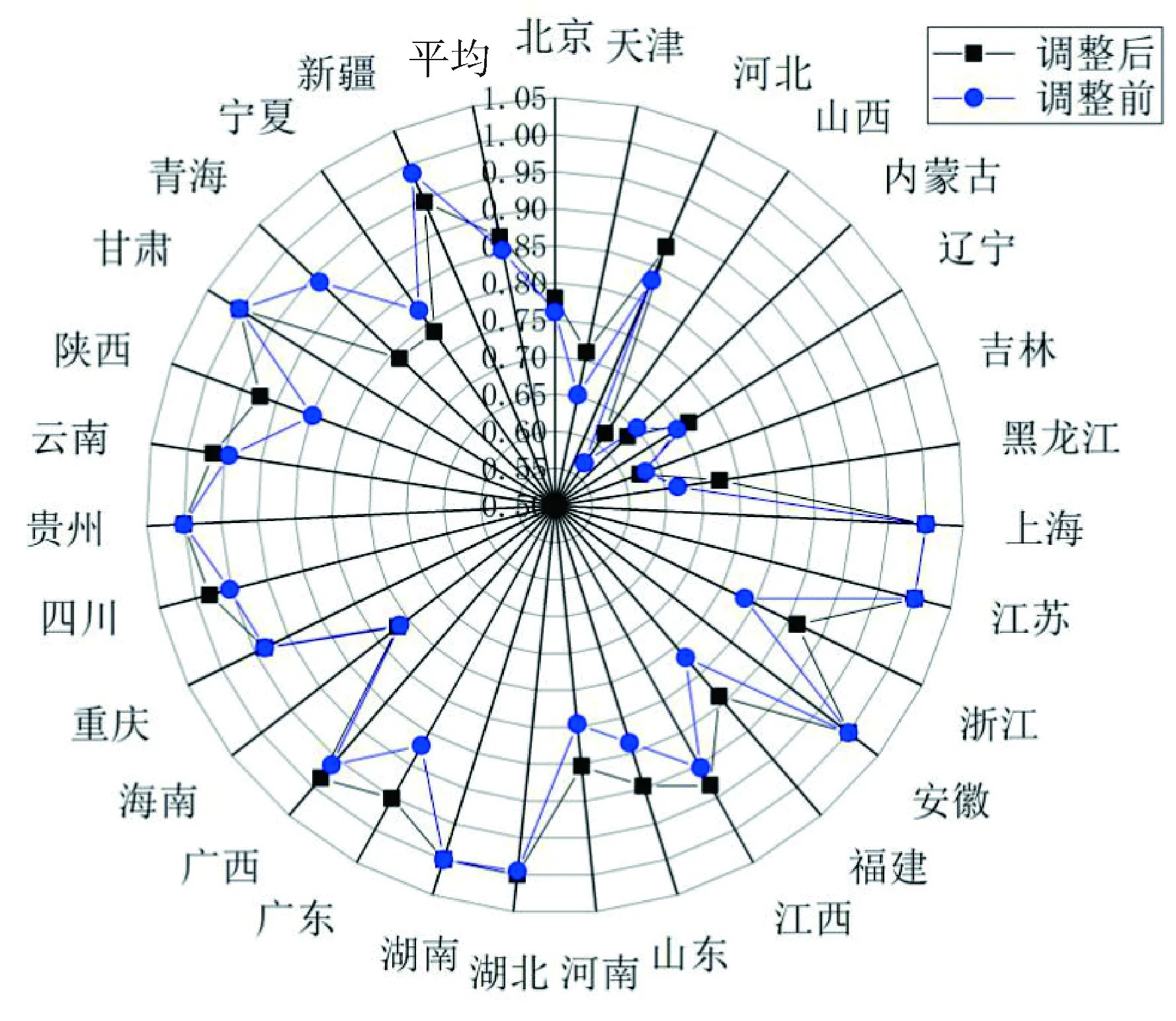
图1 中医医院三阶段DEA调整前后综合技术效率变化
图1显示,调整后湖北省中医医院的综合技术效率变为1,成为我国技术效率前沿之一的省份,全国有内蒙古、吉林、青海、宁夏和新疆5个省份的综合技术效率在调整后出现不同程度的下降,其中青海(0.788)降幅最大,为15.902%,调整后综合技术效率增幅最大的3个地区分别为浙江、广东和天津,均大于9.000%。图2为中西医结合医院三阶段DEA调整前后的综合技术效率变化,与中医医院不同,全国30个省份中西医结合医院的综合技术效率有一半省份在调整后出现不同程度的下降,其中青海、宁夏和新疆分别降低了65.174%、56.217%和20.912%。中西医结合医院中增幅最大的是浙江(0.799),为11.437%。

图2 中西医结合医院三阶段DEA调整前后综合技术效率变化
综上,可以发现在进行三阶段DEA调整后的变化具有地域性,所以接下来,我们按照中国地理区域划分标准,将30个省、直辖市和自治区分为7大区域。7大区域内中医医院和中西医结合医院的综合技术效率、纯技术效率和规模效率三阶段DEA调整前后数据整合结果如表3所示。
调整后的数据显示,综合技术效率方面,我国7大区域内中医医院平均综合技术效率均值为0.870,整体表现较好,各区域的综合技术效率存在差异,均值排序为:西南(0.970)>华中(0.951)>华东(0.933)>华南(0.901)>西北(0.880)>华北(0.725)>东北(0.686)。较调整前数据,除西北地区外,其他地区综合技术效率均值都上升;全国中西医结合医院综合技术效率均值表现较差,调整后平均效率值仅0.733,其中地区排序为:西南(0.872)>华中(0.852)>华东(0.808)>华北(0.687)>华南(0.676)>东北(0.609)>西北(0.603)。两类医院比较可见:综合技术效率排名前3的区域相同,均为西南、华中、华东地区,该地区的中医和中西医结合医院的综合技术效率处于全国领先水平,表明这3个地区中医药资源配置比较均衡,资源使用效率较高,中医医院和中西医结合医院协同发展。值得注意的是,中西医结合医院7大区域内的综合技术效率在0.700-0.799区间出现了断层,3个区域的效率值在0.800以上,4个区域处于0.700之下,两极化趋势严重,这说明我国中西医结合医院的资源配置发展不均衡,资源配置能力和资源使用效率整体上还有一定的提升空间。
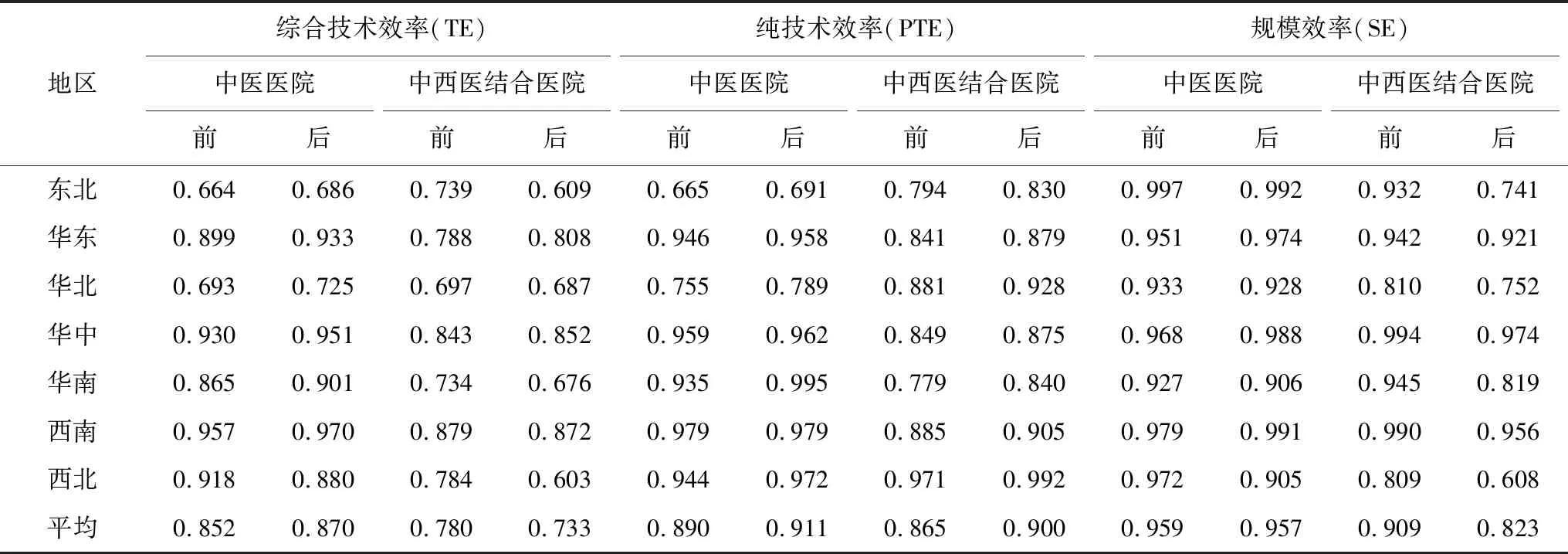
表3 我国七大区域内两类医院三阶段DEA调整前后效率情况
纯技术效率方面,除西南地区中医医院调整后均值不变外,其他地区两类医院纯技术效率均值都有不同程度提高。表3结果还显示,调整后除华东、华中以及西南地区中医医院规模效率均值上升外,其他地区的医院均值都下降,中西医结合医院各地区则全部表现为下降,因此我国中西医结合医院调整后综合技术效率均值下降的原因是规模效率的大幅下降所致。这也表明我国中西医结合医院的实际规模与最优规模间差距明显。
3 讨论
3.1 我国中医医院运行效率优于中西医结合医院
总体来看,调整后我国中医医院和中西医结合医院的综合技术效率、纯技术效率、规模效率分别为0.870、0.911、0.957和0.733、0.900、0.823,表明我国中医医院在资源配置能力、资源使用效率方面更胜一筹,这与韦柳丝等研究结果相一致[16]。从数据上来看,二者的纯技术效率相差不大,为0.011,而规模效率却相差显著,高达0.134,这也是我国中医医院运行效率优于中西医结合医院的原因。《中医药发展战略规划纲要(2016-2030年)》明确指出积极创造条件建设中西医结合医院,推进中西医资源整合是本次规划的重点任务。当前,我国中西医结合医院建设正在稳步推进,但从数据来看医院规模仍然是制约中西医结合医院综合技术效率提高的重要因素。如果中西医结合医院的规模统筹仍居于现状,将难以提升中西医结合服务能力,推进中西医资源协同创新。建议积极探索并完善现存中西医结合政策措施,有序扩张中西医结合医院规模。
3.2 我国各地区中医医院和中西医医院运行效率有所差异
与杨雨晨等的研究类似[10],本研究也发现我国区域间卫生资源配置存在不均衡的现象。7大区域的中医医院中,除东北、华北地区外,其他地区综合技术效率表现良好,影响东北、华北地区综合技术效率的主要因素是纯技术效率,说明东北和华北地区中医医院面临管理效能低下等问题。中西医结合医院,东北、华北、华南、西北地区综合技术效率表现均不佳,主要因规模效率的限制导致。各区域资源配置不均,尤其是优质医疗资源,如人才和技术都不同程度地集中于经济较发达地区,这也就提示了各地区需要兼顾经济与资源投入的公平,引导各区域医院优秀人才和新技术均衡发展。
3.3 环境变量对中医医院和中西医结合医院的运行效率影响较大
分析环境变量对投入产生的影响时,两类医院投入变量松弛值的影响全部来源于管理无效率。城市人口密度与中医医院和中西医结合医院机构数松弛值呈显著正向关系,人口密度的上升会带来地区医院机构数冗余,医疗机构效率反而降低[11]。城市人口密度是地区发展的重要驱动因素,人口密度上升提高了居民就医的选择性,导致医疗资源过度集中、配置效率降低。整体上地区生产总值对中医医院和中西医结合医院医疗投入的影响并不显著,可见医院运营效率的提高与经济发展程度并非完全相关。然而,Zheng等运用四阶段DEA模型对2010-2016年我国公立医院运行效率的分析发现,职工数与人均GDP成正比,这意味着增加医院卫生技术人员不利于医院相对效率的提高[12]。LIU等对重庆县级公立医院效率增长的决定因素的研究发现GDP对效率的增长不显著[13],这一点与我们的观点一致。相比于地区生产总值,总抚养比和病死率对中医医院医疗投入的影响更加显著,整体上均对两类医院运营效率产生正向促进作用。这可能是由于二胎的开放与老龄化现象的加剧致使总抚养比和病死率上升,导致支出增加、医疗服务需求增大,从而提高了我国医院的运行效率[14]。在本文中,政府财政拨款对中医医院和中西医结合医院机构数的影响均显著[15],但与中医医院运行效率呈正相关,与中西医结合医院运营效率却表现为负向抑制。因此各地区政府需调整对各类医院的卫生投入比例,以达到调整其数量和规模的目的,从而提高相应运营效率和服务条件。
为提高医院的运行效率,我们提出以下意见。①均衡医疗资源的配置,让资源在合理分配的基础上向发展不充分的地区倾斜;关注中西医结合医院,提升其整体运行效率。②中医医院和中西医结合医院的运行效率由不同原因导致,对于“纯技术效率改进型”的中医医院,要以提升医院管理和决策水平为重点,对于“规模效率改进型”的中西医结合医院,要以提高规模效率、适度开展规模经营建设为重心。③继续深化医疗改革,完善医保体制,搭建省际医共体,合理分配人员、物资、财产等中医药资源,为我国中医医院与中西医结合医院提供良好的外部合作环境,从而更好地发挥政府资源配置职能,使中医药资源配置达到更优效果。
