基于海洋调查实测资料的中尺度涡旋识别结果的验证及边界拟合技术

彭汉帮，王金虎，吴克亮，杨春辉

( 1.解放军92192部队，浙江 宁波 315122)

1 引言

中尺度涡旋是大洋中广泛存在的一种海洋现象，海洋中的中尺度涡旋对海洋中的水文物理性质有着重要影响[1–2]，在海洋中扮演着重要的角色。西北太平洋海域每天分布着几十个中尺度涡旋，这些中尺度涡旋水平尺度为几十千米到百千米量级[3–4]。无论从海洋动力学等理论研究方面还是从国防军事等实际应用方面，西北太平洋中尺度涡旋都具有很高的研究价值。涡旋的识别是中尺度涡旋研究的重要内容之一，也因此成为国内外学者研究的重点[3,5]。

目前中尺度涡旋的识别方法可主要归为4类：基于物理参数的 O−W（Okubo–Weiss）法、基于流动几何学的WA（Winding-Angle）法、海表面高度异常（Sea Level Anomaly，SLA）等值线法和O−W与SLA综合识别法（下文简称综合法）。O−W法通过定义W参数（Okubo–Weiss参数）对涡旋进行判断，在进行涡旋识别时，通常采用W的一个阈值圈定涡旋的形态和位置[6–7]。WA法是一种基于流场中瞬时流线的几何状态识别中尺度涡的涡旋自动识别算法，其主要思想是通过计算并挑选闭合的流线来达到识别涡旋的目的，该算法由Sadarjoen和Post[8]首次提出。SLA法根据SLA的绝对值大于某个设定的阈值来界定冷暖涡旋的形态[9–10]。综合法首先使用O-W方法识别出涡旋存在的区域，再利用SLA的极值找出涡旋的中心，最后利用SLA等值线找出涡旋的边界[11]。

为了定量评判中尺度涡旋识别方法的优劣，Chaigneau等[10]定义了识别准确率（the Success of Detection Rate，SDR）和识别冗余率（the Excess of Detection Rate，EDR）两个参数。SDR表征某种涡旋识别算法对海区涡旋的成功检测率，EDR表征该算法检测涡旋的冗余比例。因此SDR越高，EDR越小，说明该算法对涡旋识别的准确性越高。Yi等[11]利用SDR和EDR分别对O−W法、WA法和综合法进行检测，结果显示综合法SDR最高且EDR最小。综合法基于海区的SLA资料对涡旋进行识别，涡旋边界用SLA的闭合等值线表示、涡旋中心点用SLA>区域极值点表示[11]。然而SLA只是中尺度涡旋引起的海表面高度异常，并不能反映涡旋的全部性质。因此，综合法识别出的涡旋边界形态是否代表真实涡旋的水平形态、识别的中心点与实际的涡旋中心点是否一致等仍是研究者需要解决的问题。目前包括综合法在内的各类涡旋识别方法，其识别结果均缺少实测资料的检验。因此本文利用涡旋的实测资料，通过诊断涡旋的边界和中心点来诊断综合法的识别效果。

得益于中尺度涡旋识别方法的发展和卫星观测资料的日益增多，一大批针对海洋中尺度涡旋的统计特征分析也相继出现[12–15]。其中在对中尺度涡旋的水平尺度进行统计分析时，Chen等[13]采用圆半径表征涡旋的水平尺度；Wang等[12]和杨光[14]将涡旋边界东西向最长距离与南北向最长距离平均的一半作为涡旋的半径；江伟等[15]将涡旋边界各个方向离中尺度涡旋核心位置的距离平均值作为中尺度涡的半径。由此可见，为了描述中尺度涡旋，多数学者利用圆来表征涡旋的水平形态，并利用圆半径表征涡旋的水平尺度。然而江伟等[15]指出，实际海洋中水平形态接近圆形的中尺度涡旋占极少数，更多的是接近椭圆形，但对于该说法并未给出相关的证明。为了评判圆和椭圆对涡旋水平形态表征的优劣，本文基于综合识别法，分别利用圆和椭圆对其识别的边界进行拟合，通过设置一定的比对参数评判二者的拟合效果。

文章的第二部分介绍本文使用的数据和涡旋综合识别法；第三部分为利用实测数据诊断识别涡旋的边界、中心点；第四部分为涡旋边界拟合效果的比对；最后是总结和讨论。

2 数据和方法介绍

2.1 数据介绍

本文所用的海表面高度计资料来自于哥白尼海洋环境监测局（Copernicus Marine and Environment Monitoring Service，CMEMS）。该卫星观测资料由 T/P、ERS、Sentinel-3A、Jason-3、HY-2A、Saral/Altika 等多颗卫星高分辨率海面高度异常数据整合而成，可以准实时地为世界上主要的海气预报中心提供服务。其时间分辨率为日平均，即每天提供1个全场卫星观测数据，空间分辨率为（1/4）°×（1/4）°。

涡旋实测数据来源于2019年一次远海综合调查测量航次中对一个冷涡进行的观测，其中心位置位

于 18.2°N，128.5°E 附近（图1）。走航观 测航线 为A→B→C→D→E→F→G→H→I→J→A，并在其中两条断面上开展13个大面站观测。走航时采用300 kHz ADCP对上80 m层海流进行观测，最上层观测深度为10 m，垂向采样间隔为2 m；采用38 kHz ADCP对上900 m层海流进行观测，最上层观测深度为38 m，垂向采样间隔为16 m；选取300 kHz ADCP的80 m以浅和38 kHz ADCP的80 m以深的海流数据用于本文的研究。对航线中横跨涡旋东西方向的FG断面、 横跨南北方向的AJ断面，利用下放CTD对温盐剖面进行测量，测量深度为2 000 m；温盐观测站点中，W1至W7相邻站点距离约为33 km，W8至W13相邻站点距离为28～75 km。

2.2 涡旋识别综合法

本文借鉴Yi等[11]发展的涡旋识别综合法，综合法按照确定涡旋位置→确定涡旋中心点→确定涡旋边界的先后顺序，对海洋中的中尺度涡旋进行识别。具体过程如下：（1）利用O−W参数W确定涡旋的位置，W<−0.2σ（σ为W的空间标准方差）的区域为涡旋的核心区域；（2）采用 3°×3°的区域窗口，找出研究海域所有窗口内SLA的极值点；（3）位于涡旋核心区域内的SLA极值点作为涡旋的中心点；（4）以0.5 cm的间隔绘制SLA等值线；（5）去除非闭合或者直径大于500 km的闭合等值线；（6）选取包含涡旋的核心区域和中心点的最小闭合等值线作为涡旋的外边界。

2.3 圆与椭圆拟合法

本文拟合的对象是闭合的涡旋边界。采用的圆拟合法首先分别以闭合边界上的横坐标和纵坐标平均值作为圆心的横坐标和纵坐标，再取闭合边界上的点到圆心的平均距离作为圆半径，最后绘制圆形如图2a所示。

图2 涡旋边界的圆拟合（a）和椭圆拟合（b）结果Fig.2 Circle (a) and ellipse (b) fitting results of the eddy boundary

本文使用的椭圆拟合法来自Gander等[16]开发的最小二乘法椭圆拟合法。最小二乘法椭圆拟合是较常用的椭圆拟合方法[17–18]，其主要技术是寻找参数集合，从而将数据点与椭圆边界之间的距离度量最小化，常见的距离度量有几何距离和代数距离[19]。无论是几何距离还是代数距离，其目的就是求如椭圆一般方程式（1）的解，从而根据方程系数A、B、C、D、E和F的值确定涡旋长轴、短轴、焦点和倾斜角等参数。根据获取的涡旋参数，绘制椭圆如图2b所示。

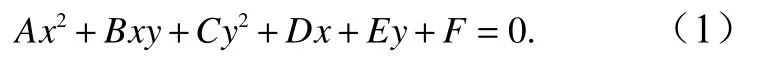
3 综合法涡旋识别结果的诊断

3.1 涡旋识别边界的诊断

本文利用实测流场诊断涡旋识别的边界。由2.2节内容可知，综合法识别出的涡旋边界是SLA闭合等值线，因此欲诊断识别的涡旋边界，应选取上层的实测海流数据。本文选取200 m以浅中15 m、50 m、100 m和200 m为代表的标准层实测海流数据，用于诊断涡旋边界形态。如图3所示，实测流场为15 m、50 m、100 m和200 m层平均流场，红实线为识别涡旋的边界。从图3可以看出，该冷涡主体部分（17°N以北）大致呈倾斜椭圆状，实测流场围绕该椭圆逆时针旋转，与识别的涡旋边界形态较为吻合。因此，识别的涡旋边界形态基本可以反映实测涡旋水平形态。

图3 涡旋边界（红线）与实测流场（流场为15 m、50 m、100 m和200 m层平均流场）Fig.3 The eddy boundary (red line) and observed currents average of 15 m, 50 m, 100 m and 200 m

为进一步诊断识别的涡旋边界形态与实测涡旋水平形态的吻合情况，如图4所示，分别将15 m、50 m、100 m和200 m层流场与涡旋边界投影到一个平面上，从各层流场中选取位于涡旋边界附近的实测海流点（为保证诊断数据的质量，实测海流点与涡旋边界点间的水平距离控制在2 km范围内）。通过计算每个实测海流点的流矢量与涡旋边界切线的夹角α诊断识别涡旋的边界形态与实测涡旋的形态吻合度，α越小说明识别的涡旋边界形态越能反映实测涡旋的水平形态。结果显示15 m层α在0.6°～30°范围内，平均值约为 12.8°；50 m 层α在 0.4°～32°范围内，平均值约为 13.8°；100 m 层α在 1.3°～36°范围内，平均值约为 14.6°；200 m 层α在 2.2°～38°范围内，平均值约为14.9°。因此，识别的涡旋边界形态基本可以反映实测涡旋水平形态。

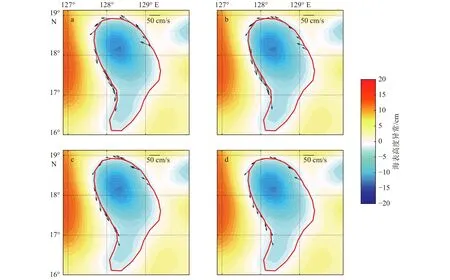
图4 涡旋边界及其附近15 m (a)、50 m (b)、100 m (c)和200 m (d)层实测流场Fig.4 The eddy boundary and the nearby observed currents of 15 m (a), 50 m (b), 100 m (c) and 200 m (d)

3.2 涡旋中心位置的诊断

本文利用实测海流和温度数据反演涡旋的中心位置，并用来诊断识别的涡旋中心位置。由图1可知，航次任务对涡旋进行观测时，根据综合法识别结果，选择分别位于中心点的北面和南面两个纬向断面（FG和HI断面）进行走航式海流观测。由图3可知，该冷涡主体部分大致呈椭圆形，且长轴呈西北–东南走向。由于椭圆长轴两端曲率大，因而涡旋在此处流向变化大和流速小。根据此特点，利用FG和HI断面的海流数据（200 m以浅平均海流）可以反演出该椭圆涡旋的长轴线（本文记为涡旋中心线，如图5a所示），并初步判断实际涡旋中心位置大致位于该中心线上。同时，根据冷涡中心温度较低的特点，通过计算涡旋内每个大面观测站剖面200 m以浅平均温度，可以进一步缩小涡旋中心位置的分布区域（本文记为中心区域），如图5b所示。由图5b可知在该冷涡区域内所有观测站点200 m以浅平均温度中，W4、W5和W10这3个站点是温度最低的3个点。同时从图5c温度剖面图可以看出，W4、W5和W10站点的温度剖面处于低温一侧。由于温度由冷涡中心向外呈增加趋势，可以判断涡旋中心不会出现在站点 W4至W3和W11、W5至W6以及W10至 W9区域内，而大概率出现在由站点W4、W5和W10围成的区域内。根据以上推断，利用经过同一平面内不在同一条直线上的3点可确定一个圆的定理，可基于W4、W5和W10 3个站点反演出冷涡的中心区域（如图5b中的红圆所示）。

结合实测资料反演的涡旋中心线和中心区域，通过求二者的“交集”可以进一步缩小实际涡旋中心的位置范围。如图5d所示，涡旋中心线与中心区域圆相交于弦AB，故可将涡旋中心位置锁定在弦AB上。通过距离计算，识别中心点C至弦AB的最小距离为C到D的距离（约8 km），最大距离为C到B的距离（约25 km）。因此，综合法识别的中心点与实测资料反演的涡旋中心点距离范围在8～25 km之间，由于本文用到的卫星高度计资料空间分辨率为（1/4）°×（1/4）°（约28 km），因此可以说两中心点位置较为吻合。

4 涡旋边界拟合的准确率

本文从两方面比对圆与椭圆对识别涡旋边界的拟合效果。第一个是识别边界区域和拟合边界区域重叠和不重叠部分的面积占识别边界区域面积的比例，即重叠率（Overlap Rate, OR）和冗余率（Redundancy Rate, RR），表达式分别为式（2）和式（3）；第二个是拟合结果与SLA反演的地转流吻合度，即地转流矢量与拟合边界切线的夹角α大小。显然，OR越大，RR、α越小，拟合效果越好。

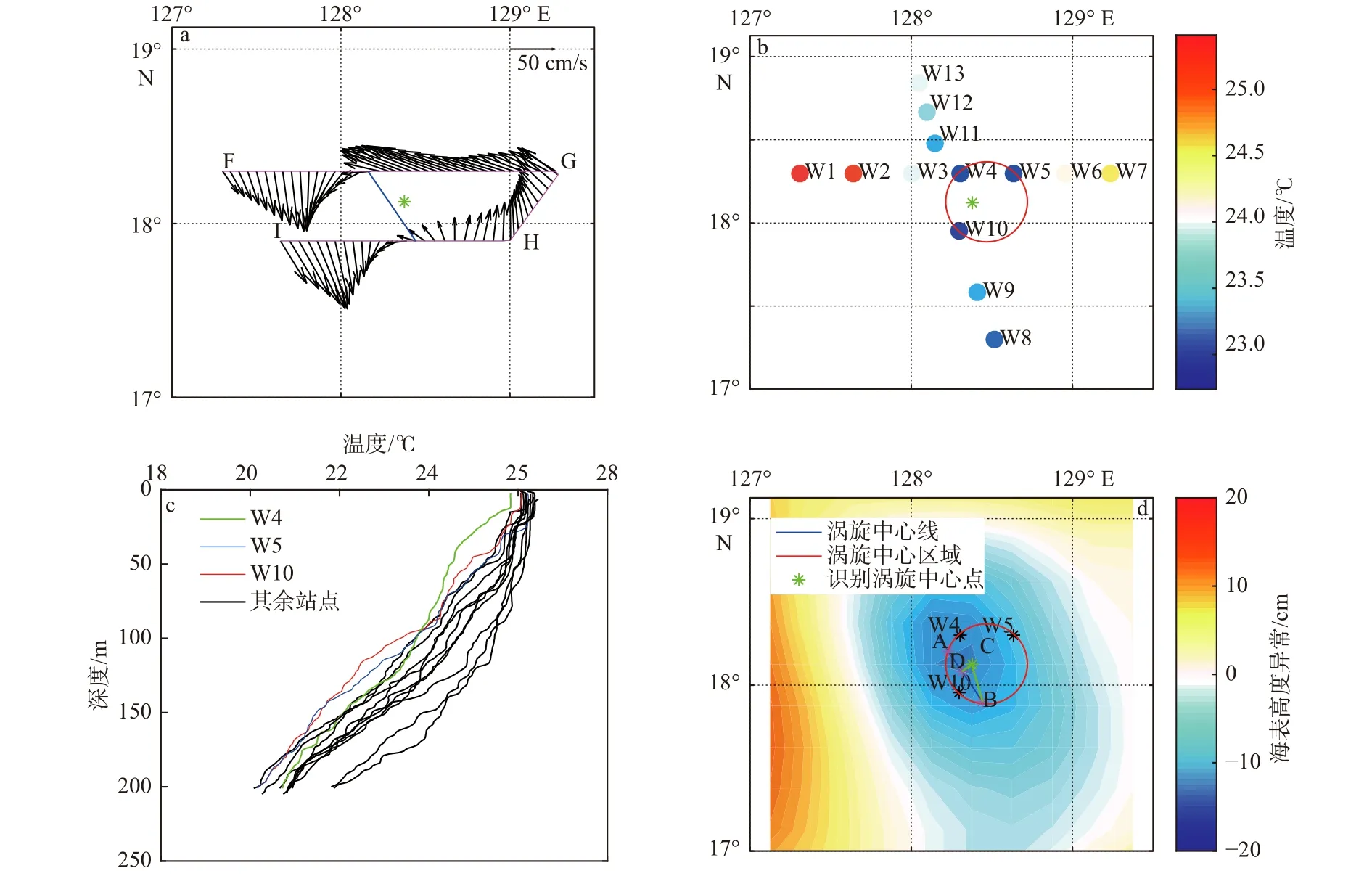
图5 基于实测数据的涡旋中心位置诊断过程Fig.5 Diagnosis processes of the eddy center based on observed data

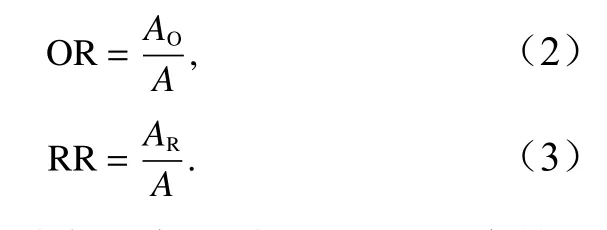
为叙述方便，分别将涡旋识别边界、圆拟合结果和椭圆拟合结果围成的区域简称边界区域、圆区域和椭圆区域。式中，A为边界区域面积；AO为圆区域或椭圆区域与边界区域重叠部分的面积；AR为圆区域或椭圆区域中与边界区域不重叠部分的面积，如图6所示。

图7a为西北太平洋海域某个涡旋分别进行圆和椭圆拟合的结果。通过计算可知，该涡旋边界区域的面积A为6.8（本文近似的将地理坐标中1°×1°围成的面积记为1），圆区域中与其重叠的面积AO为5.3、与其不重叠的面积AR为2.5，因此该涡旋边界圆拟合的结果OR为0.78、RR为0.36；椭圆区域中与边界区域重叠的面积AO为6.5，与其不重叠的面积AR为0.6，因此椭圆拟合的结果OR为0.95、RR为0.09。

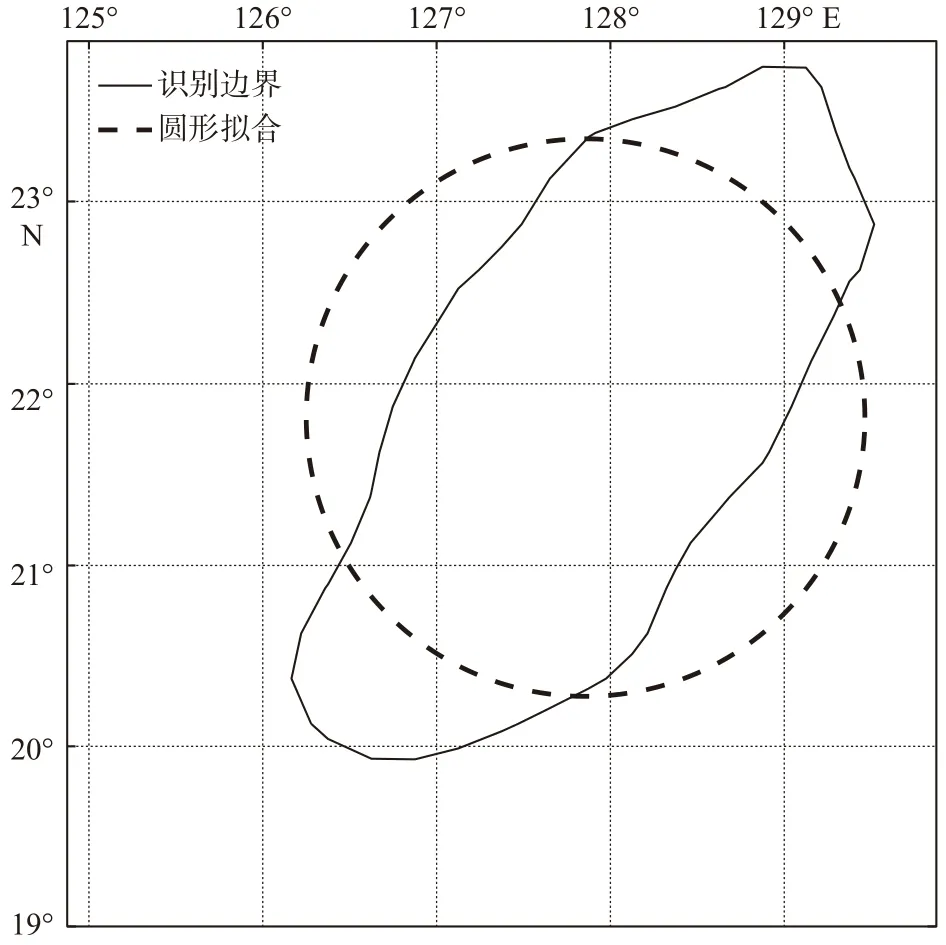
图6 边界区域与圆区域叠加Fig.6 The eddy boundary overlaps with the circle

与3.1节中利用实测海流点诊断涡旋边界方法相似，从地转流中选取与拟合边界距离最近的地转流点（如图7b所示），通过计算地转流矢量与拟合边界切线的夹角α诊断边界拟合效果。结果显示，圆与椭圆平均α分别约为33°和10°。因此，就图7a所示的涡旋识别的边界而言，综合考虑OR、RR和α，椭圆拟合效果比圆更佳。

为进一步比对圆与椭圆对涡旋边界的拟合效果，本文随机选取西北太平洋某区域，对该区域进行涡旋识别并分别进行圆与椭圆拟合（如图8a所示），计算每个涡旋的OR和RR。同时从地转流中选取与拟合边界距离最近的地转流点（如图8b所示），计算每个涡旋的平均α。OR、RR和α结果如表1所示，从表中可知： （1）该区域9个涡旋中，有8个涡旋椭圆拟合OR大于圆拟合OR、椭圆拟合RR有7个小于圆拟合RR；（2）圆拟合 OR平均为 0.83、RR平均为 0.26，椭圆拟合OR平均为0.88、RR平均为0.17；（3）有9个涡旋椭圆拟合α小于圆拟合α，平均小8.3°；（4）椭圆拟合OR方差与圆拟合OR方差相等，椭圆拟合RR、α方差分别小于圆拟合RR、α方差。因此，综合考虑OR、RR和α的结果，可以得出的结论是利用椭圆比利用圆拟合涡旋边界效果更佳。

5 结论

本文在涡旋OW与SLA综合识别法的基础上，利用实测资料对识别的涡旋形态和中心点进行比对验证。结果表明综合法识别的涡旋与实测结果吻合度较高。

图7 单个涡旋边界拟合结果（a）（矢量箭头为地转流）及拟合边界附近地转流分布（b）Fig.7 Fitting results of the eddy boundary (a) (vectors indicate the geostrophic current) and the distribution of geostrophic current nearby the fitting boundary (b)

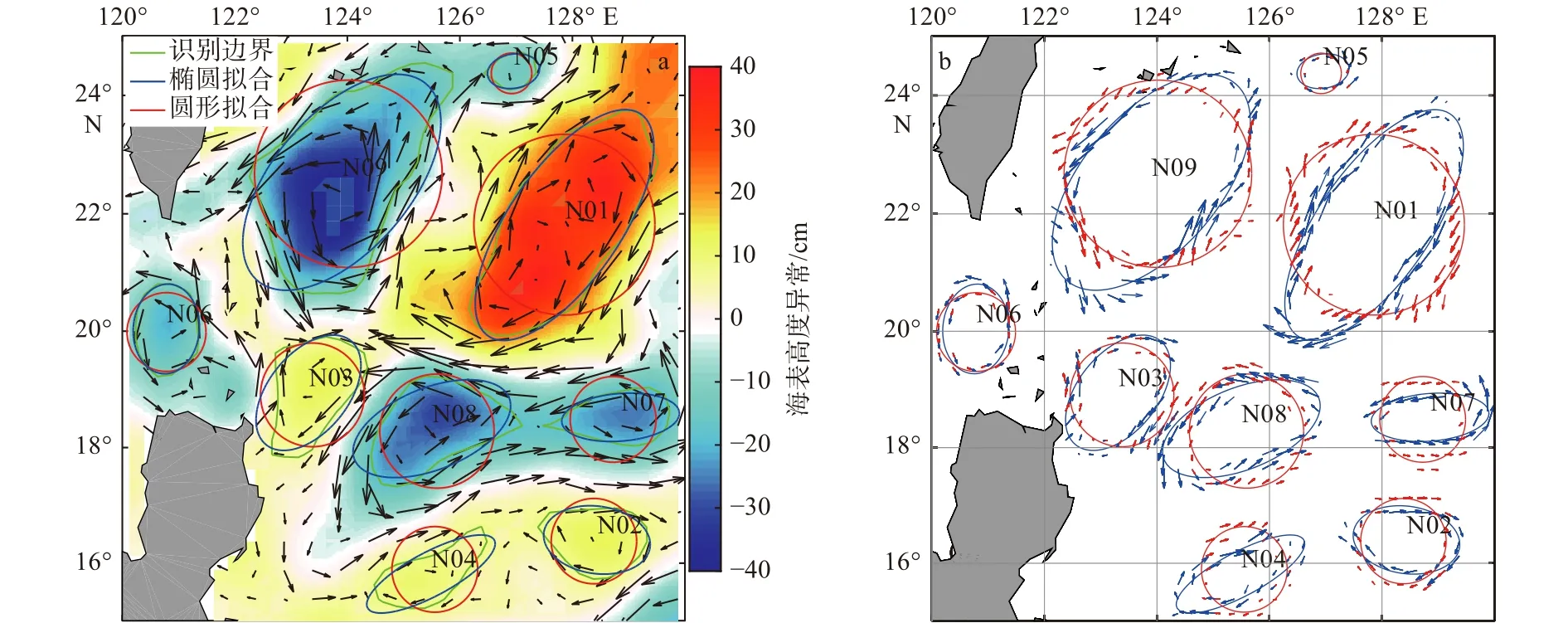
图8 多个涡旋拟合结果（a）及其拟合边界附近地转流分布（b）（Nxx为涡旋编号）Fig.8 Fitting results of several eddy boundaries (a) and the distribution of geostrophic current nearby the fitting boundaries (b) (Nxx denote the eddy number)

表1 N01–N09号涡旋圆与椭圆拟合结果（OR、RR和α）Table 1 The results (OR, RR and α) of circle and ellipse fitting for number N01 to N09 eddies

本文通过诊断涡旋边界附近的实测海流矢量与涡旋边界夹角α来评判涡旋边界与实测涡旋水平形态的吻合度。通过计算15 m、50 m、100 m和200 m层实测海流矢量与涡旋边界的夹角α，结果显示α平均在12.8°～14.9°范围内，因此可以判断综合法识别的边界形态能够较好地反映实际涡旋的水平形态。

本文利用实测海流和温度剖面资料反演实际涡旋中心位置，并与识别的中心位置进行比对，结果显示涡旋识别的中心位置与实测涡旋中心位置基本吻合。比对过程如下：（1）根据涡旋产生的旋转流，利用涡旋中心线处流向变化大、流速小的特点确定涡旋中心线；（2）利用冷涡中心温度较低的特性，分别对涡旋内每个温盐观测站点200 m以浅温度剖面求平均值，选取平均温度较低的3个站位点并以此圈定涡旋中心区域；（3）涡旋中心线和中心区域共同确定的涡旋中心与涡旋识别的中心点距离范围在8～25 km，小于卫星高度计资料的空间分辨率（28 km）。

本文随机选取西北太平洋某个海域，比对圆与椭圆对识别涡旋的边界拟合效果。利用拟合参数面积重叠率、面积冗余率和地转流矢量与拟合边界夹角诊断拟合效果，结果显示椭圆OR比圆OR平均大0.05、椭圆RR比圆RR平均小0.09、椭圆α比圆α平均小8.3°。可以看出椭圆拟合效果要明显高于圆拟合效果。

本文在研究中存在以下几点不足：（1）仅利用1个涡旋的实测资料进行识别结果的诊断，得出的结论不具备足够的说服力；（2）由于涡旋的观测时间跨度为3 d，而涡旋识别利用的SLA数据的日期为涡旋观测期间的某一日。考虑到西北太平洋中的涡旋在以每天约10 km的量级向西传播[3]，本文在利用实测数据对识别涡旋边界和中心点进行比对验证时，会存在一定的误差。下一步将结合更多的涡旋同步观测资料进一步验证涡旋识别结果，并利用椭圆识别开展相关的研究。