对地协同观测混合星座多目标优化设计
2021-03-02贺波勇曹静周庆瑞王建国
贺波勇, 曹静, 周庆瑞, 王建国
(1.西安卫星测控中心 宇航动力学国家重点实验室, 陕西 西安 710043; 2.西北工业大学 航天学院, 陕西 西安 710072;3.中国空间技术研究院 钱学森空间技术实验室, 北京 100094; 4.中国人民解放军91515部队, 海口 三亚 572016)
混合星座是指由携带功能相似或功能不同的有效载荷,为协同完成某项任务而组合在一起的2个或2个以上子星座构成的复合星座。对地观测卫星主要有电子侦察卫星、光学成像卫星和合成孔径雷达(synthesized aperture radar,SAR)成像卫星等类型。电子侦察卫星通过无线电信号定位,幅宽可达2 000~3 500 km,但探测精度较低(约10~30 km),且只能对目标进行定位。光学成像卫星可分为可见光成像和红外成像,可见光需要满足一定的光照要求,而红外成像可以实现全天时目标探测,空间分辨率高一般在0.1~2 m之间,但使用轨道高度较低,幅宽通常只有30~60 km。SAR最高可实现0.1~0.3 m的探测分辨率,具有全天候成像功能,不足之处与光学成像卫星相同,幅宽只有30~60 km[1]。可见,协同利用多种卫星不同优点,可以实现较高对地观测效率,获取高品质信息[2-3]。然而,我国目前对地观测主要是单星应用或少数几颗卫星配合应用,难以应对日益增长的对地观测任务需求[4]。
可以将现有星座设计方法分为3类:①几何解析法,一般卫星数目较少,不需要星间链路,可以通过轨道力学领域知识进行分析设计;②基于仿真计算的比较评估设计法,依靠轨道力学领域知识拟定多种方案,通过计算和比较每种方案的性能指标,人工优选[5-6];③基于现代优化算法的设计方法,这类方法通常将卫星数目、分布轨道面数目和部分轨道参数一起编码,采用数千次迭代得到计算结果。该方法用于同构星座设计时设计变量数目大幅减少,便于计算收敛,如遗传算法[7]、复形调优法[8]等。传统优化星座时,在满足基本地面覆盖指标情况下,一般将星座部署代价(可简化为卫星数目)作为权值最大的一个优化指标[9],得到的星座并不实用[10]。实际星座部署代价工程计算模型非常复杂,涉及卫星数目、卫星平台、载荷、电源系统、能否一箭多星发射、不同运载火箭差价等航天工业品市场价格因素,星座中卫星运行轨道高度又直接影响地面覆盖性和对地分辨率,这又和观测载荷的型号选择相关,又与卫星平台、电源系统、火箭型号相关[11]。混合星座中不同轨道高度的卫星受摄动影响,构型自然保持时长和构型保持控制所需代价也是混合星座必须考虑的优化设计指标,文献[12]设计的全连通星间链路星座的不足是忽略了构型稳健保持问题。文献[13]利用大偏心率椭圆冻结轨道和赤道圆轨道组成的异构预警星座避免了构型摄动保持问题,但大椭圆轨道不适合要求稳定分辨率的对地观测任务。随着经济发展和航天产品的商业市场化,卫星制造成本大幅降低,对地观测数据对国土资源、海洋监视、商业经济、气象预报、环境保护、灾害监测、军事支援等方面的支撑作用日益突出,星座对地观测的时间效率、空间分辨率和遥感信息即拍即传等功能的优化指标权重需大于星座部署代价指标。
针对以上问题,结合我国现有卫星性能,提出了考虑星间链路的对地观测混合星座多目标优化设计模型,并验证模型的合理性。
1 问题描述
星座设计是指同时设计多个卫星任务,用以协同完成某一特定任务,一般包括卫星类型、个数、工作轨道,相互协同工作关系以及发射部署和长期构型保持等因素。
1.1 设计目标
星座设计目标主要有对地观测性能品质和成本两方面指标,而对地观测性能品质又可分为全球普查覆盖率、区域详查时间分辨率、空间分辨率、星间链路性能等指标,成本主要有星座部署成本和长期运控成本。
1.1.1 全球普查覆盖率
1) Walker星座覆盖率
Walker星座是全球覆盖最有效的星座,可用[(N/P/F),(h,i)]共5个参数描述[14]。(N/P/F)为离散正整数,分别为卫星总个数,分布轨道面数和相位因子F=0~(P-1)。(h,i)分别为轨道高度和轨道倾角,Walker星座默认所有卫星高度和轨道倾角相同。升交点赤经
Ωi=Ω0+i·ΔΩi=1,…,P-1
(1)

全球普查覆盖率主要由倾角i、轨道高度h和对地观测卫星的波束半张角θ决定,如图1所示,全球覆盖率为
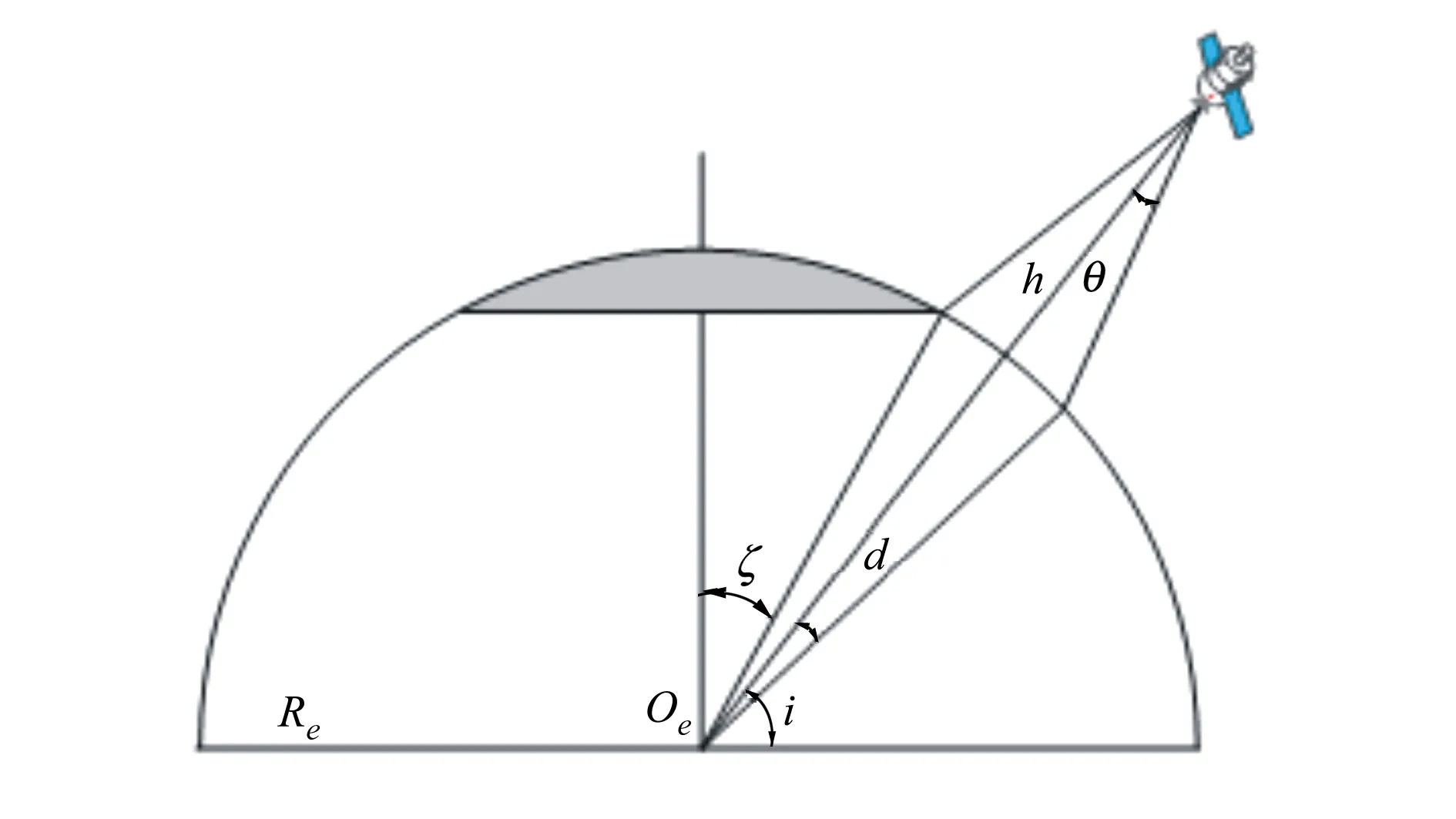
图1 对地观测几何

(2)
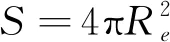

(3)


(4)
2) 异构星座覆盖率
异构星座的全球覆盖率需要遍历搜索计算,涉及地表网络划分方法,传统的等经纬度方法会在两极产生密集而无用的点,等纬度带划分法虽然较等经纬度方法有所提高,但存在网格不均匀缺点[15]。

表1 正二十面体顶点坐标
正多面体是比较均匀的方法,马原野[16]推荐正二十面体划分方法。该方法是利用相互垂直的黄金矩阵,顶点坐标如表 1 所示。然后不断将球面三角形4等分细化,细分3次后北极视角如图2所示,蓝色点是三角形中心点,则无旋地球(瞬时)任意点到某轨道面距离如图3所示。

图2 北极地区网格
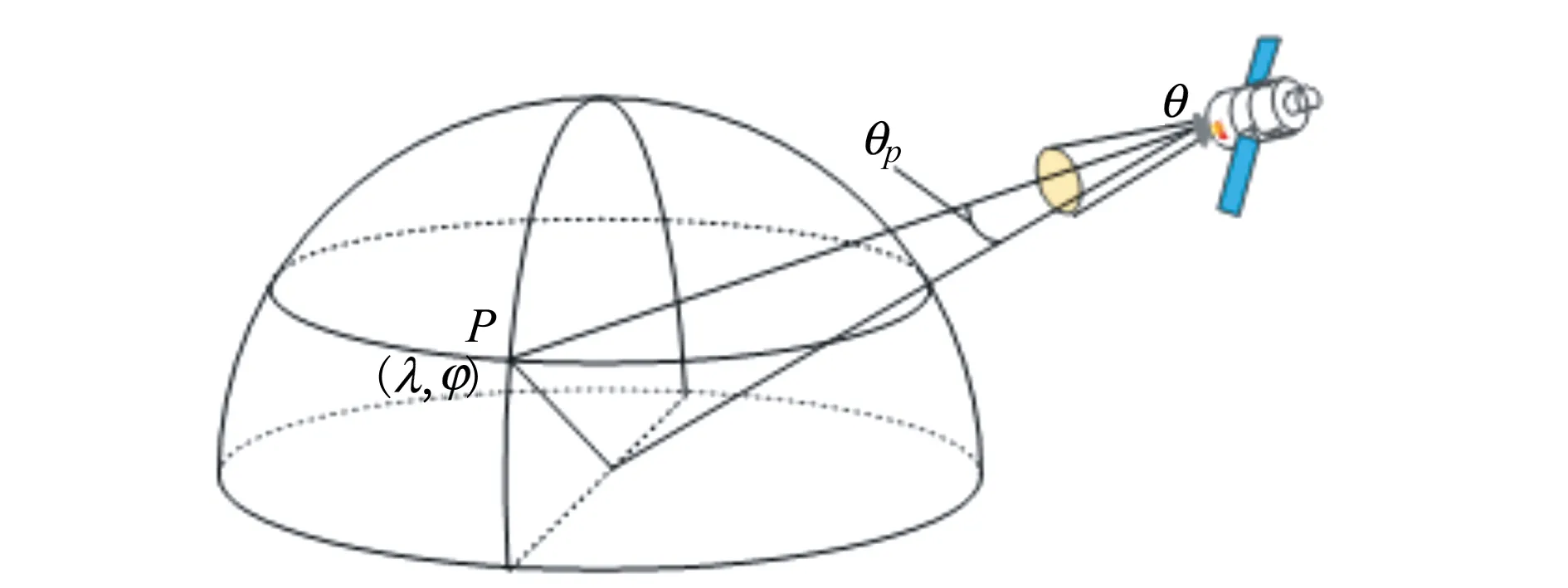
图3 地面覆盖带示意图
地面P点(地球半径为Re)在J2000.0坐标系中可由赤经赤纬(λ,φ)表示

(5)
对地观测卫星在J2000.0坐标系中位置为
psat=[x,y,z]T
(6)
在卫星载荷姿态无侧摆情况下,计算地面网格中心点与卫星和地心构成的三角形中卫星所在顶点角度θp。若θp≤θ,则该地面位置能被该颗卫星覆盖,否则,不能覆盖。该算法需要搜索计算所有网格点中心和卫星一个周期的所有位置。在优化部署全球侦察星座时,一个重要指标即是该星座对全球的覆盖率

(7)
式中:Ntotal为球面网格划分总数;Ncov为覆盖网格数;通常η≤1。也可根据不同任务对不同区域的侦察重要性增减权值,如对于环境监测任务,两极区域人类活动较少,可减小权值,但对于气象预报任务,不可减小两极区域权值。
1.1.2 观测时间分辨率
1) 电子侦察Walker时间分辨率
电子侦察卫星工作不受阳光限制,例如,对于P个轨道面的Walker星座而言,时间分辨率有经度方法和轨道面内2个方向:

(8)
式中,ωe为地球自转角速度。


(9)

2) 异构星座时间分辨率
对于区域观测异构光学卫星星座而言,宜采用圆轨道卫星环“并肩扫推”方式实现对特定区域的覆盖和详查。
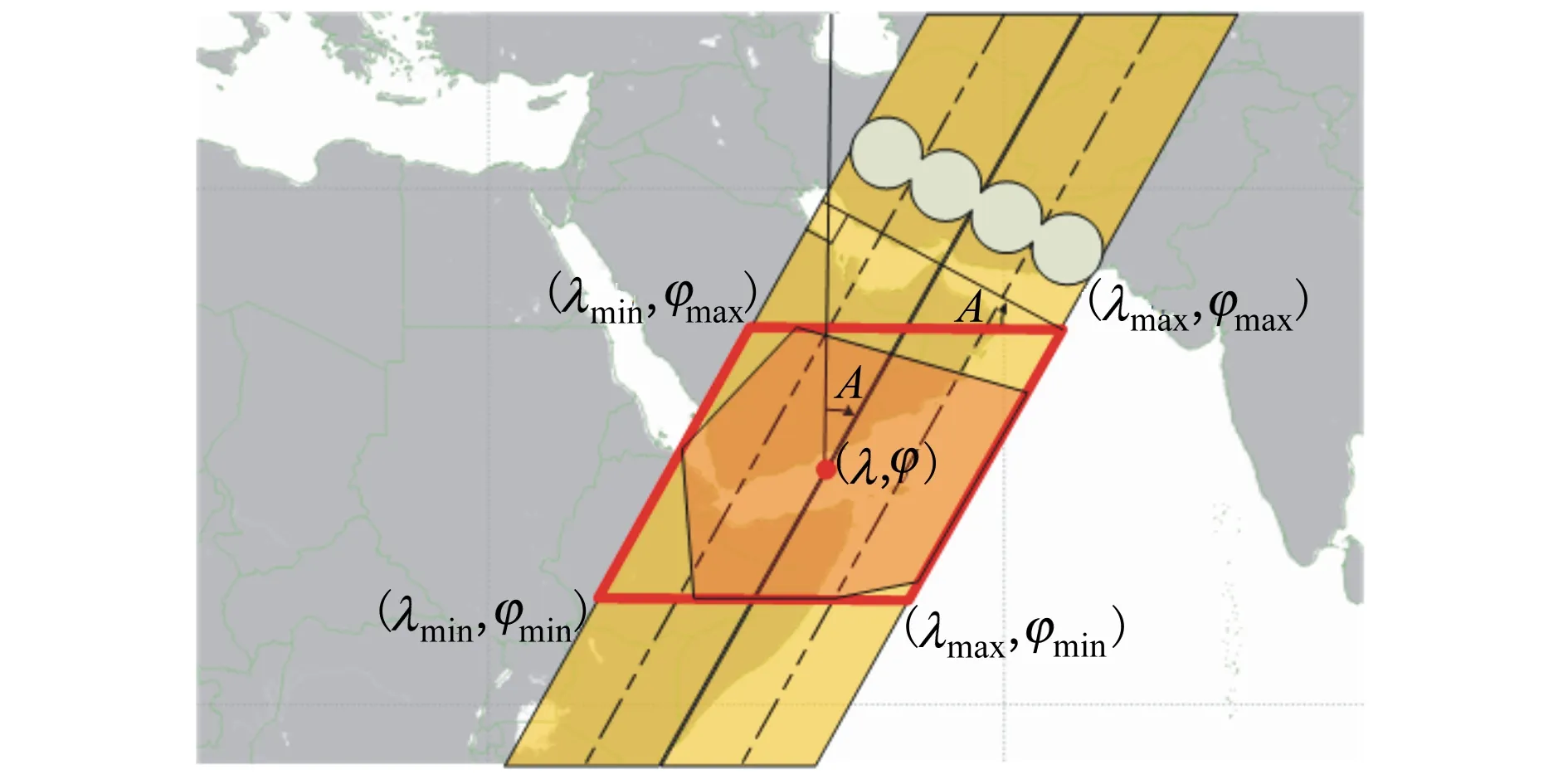
图4 外接平行四边形示意图
首先,将被观测区域以一个外接平行四边形包围,如图4所示为降轨弧段观测平行四边形,顶点坐标经纬度最大最小值分别为(λmin,λmax,φmin,φmax)。一般而言,利用太阳同步轨道上的近地光学成像卫星实现区域高分辨率详查,由运载火箭能力和载荷质量共同决定的轨道高度,轨道高度又决定太阳同步轨道的倾角,则外接平行四边形倾斜方位角为
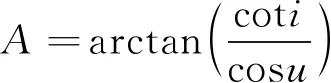
(10)
式中,u为平行四边形中心对应纬度幅角,由该点纬度φ和轨道倾角计算得到。

(11)
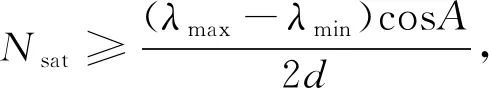
1.1.3 空间分辨率
对地观测载荷传感器主要有雷达、光机扫描和电荷耦合器件(charge couple device,CCD)等,虽然各自原理不同,但其空间分辨率Ersl都与瞬时视场θ(或孔径)和轨道高度h相关
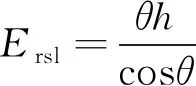
(12)
式中,θ与传感器尺寸和扫描仪焦距(或成像板像元矩阵规模)相关,其性能品质与组成器件相关,高性能意味着成本高对电源系统需求大,一般在卫星总体设计时协调卫星成本、承力结构、电源系统和热控系统等标准化综合设计。若载荷确定后,空间分辨率只与轨道高度相关[17]。
1.1.4 星间链路指标
星座长期运控成本主要来源于构型保持控制和数据传输。在星座设计之初就考虑星间链路数传不仅是实现遥感信息即拍即传需求的重要手段,也是减小数传成本的有力措施[12]。如果中轨道星座星间链路能全天候覆盖低轨卫星,建立中-低轨道星间链路,则会有效减小长期运控成本[18]。仅考虑几何关系的同平面等高度相位均布的圆轨道星间链路要求轨道高度和卫星数量存在以下关系

(13)
(13)式取等号时,设Re=6 378.137 km,则有Nsat=3,h=6 378.137 km;Nsat=4,h=2 641.9 km;Nsat=5,h=1 505.7 km;Nsat=6,h=986.7 km;Nsat=7,h=701.1 km;Nsat=8,h=525.5 km。
1.1.5 星座部署成本
星座部署成本主要由卫星数量和单星成本组成

(14)
单星成本由卫星平台、载荷和平均发射入轨成本(是否一箭多星)等因素决定

(15)
式中:s(θ)为卫星平台和载荷的成本;在同等遥感像元成像品质假设下,θ大意味着遥感像元阵列数量多,则卫星平台成本也高;s(θ)∝θ;l(h,θ,N)为平均发射部署成本;若θ较大,载荷和卫星平台均大,只能单星发射或一箭双星;h较大时,需要成本更高的火箭;若(h,θ)都较小时,可以一箭多星发射,平均到每颗星的成本会阶梯性减小。所以存在最佳的(h,θ,N)组合使Ccstl最优。对于卫星数量较多的星座,宜采用已成标准的卫星平台和可批量生产的有效载荷,并设计轨道高度一致,倾角相同的Walker星座构型。在地面分辨率要求约束范围内,可在一定程度上提成轨道高度以获取较大的覆盖角,但前提是运载火箭可以承受。
1.1.6 星座构型保持代价
一般星座设计寿命超过10年,不同轨道构型保持控制频次不同,控制策略又分为相对保持和绝对保持,后者燃料消耗代价大于前者,会减少卫星寿命[10]。混合星座往往包含2个以上星座,如果2个星座由于轨道参数差异导致漂移,往往最初的构型无法保持,且会引起数传节点路由分配重构问题[19]。文献[11]建议混合星座应分开设计,再考虑不同星座层间星间链路数传节点问题。这样,每个星座受摄轨道参数漂移情况相近,相对保持代价较小。而不同星座间数传可以设置层间路由协议。
1.2 约束条件
星座设计约束条件一般有环境约束、任务目标约束、有效载荷约束和星座构型保持约束等,约束条件除在设计参数区间限制外,有时也可通过一定的手段转化为设计目标指标。
1.2.1 Van-Allen带
南北纬40°~50°之间,高度范围分为两段:内带1 500~5 000 km,外带13 000~22 000 km。内带粒子的最大密度位于约3 000 km高度处,而外带的最大密度位于约17 000 km高度。
1.2.2 大气阻力衰减
大气阻力在500 km以上的影响较小,所以低轨高度一般在[500,1 500]km之间。
1.2.3 地面轨迹回归
轨道相对于地球旋转一周的时间间隔为

(16)
若存在既约正整数D与R使得航天器轨道周期T与Te满足
RT=DTe
(17)
则航天器D天正好运行R圈,其星下点轨迹开始重复,称为回归轨道,存在回归因子

(18)
式中,L,K均为正整数,且L≤Q,0
1.2.4 载荷工作条件
仅考虑J2项摄动时,升交点赤经的进动角速度可表示为

(19)

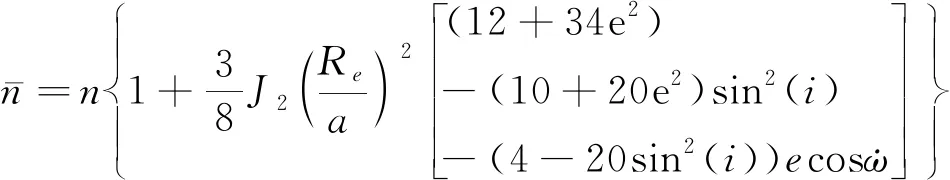
(20)


(21)
圆轨道上的卫星可以获得一致分辨率的遥感图像,便于后期图像拼接处理。可见光卫星对地面目标进行摄影时,地面目标除了要满足覆盖要求外,还应有阳光照明。稳定的阳光高度角需要太阳同步回归轨道。平太阳回归年为365.242 2个回归日,可得平太阳在赤道上移动的角速度(地球自转)为
ωs=360°/365.242 2=0.985 6°/day
(22)


(23)
对地观测载荷也可通过姿态侧摆扩展卫星地面覆盖带。最大侧摆角既可作为星座设计的约束条件,也可作为一种设计指标。
1.2.5 构型保持约束
由于卫星平运动和地球自转角速度成简单整数比时,地球田谐项摄动会对轨道半长轴产生明显的共振影响,间接导致卫星相位漂移。卫星回归周期D>5的准回归轨道可有效避免共振现象。
2 中低轨混合星座
2.1 中轨星座设计
2.1.1 中轨星座设计模型
1) 设计变量
中轨轨道混合星座中中轨卫星星座应承担全球普查和星间链路数传功能,宜将电子侦察卫星部署在Walker星座上。除描述Walker星座的5个参数[(N/P/F),(h,i)]外,卫星波束半张角θ也是中轨星座的设计变量,如姿态可以侧摆,相当于θ瞬时值变大
x=[(N/P/F),(h,i,θ)]
(24)
如果有地面轨迹回归要求,可根据(17)式计算与h近似匹配的回归因子。
2) 目标函数
对于Walker星座而言,星座构型相对保持代价较小,可在初步设计不予考虑。则剩余5个优化目标函数
(25)
式中,nisl为星座中含星间链路最少的卫星的星间链路数。由于星座部署代价指标计算涉及较多卫星、载荷、运载火箭、发射测运控市场报价情况,本文不做详细调研,仅将卫星总数和波束半张角控制在熟知区间内。
3) 约束条件
Van-Allen内带中粒子最大密度位于高度约3 000 km处,考虑卫星安全稳健性,一般选择轨道高度低于2 500 km。Walker星座全球覆盖指标要求轨道倾角接近π/2,由(4)式可知,选择合适的轨道高度和波束半张角可使Walker星座全球普查覆盖率保持100%的情况下,倾角在π/2附近一定区间内设计。
2.1.2 混合参数分层求解策略
图5给出了混合参数分层设计框架,将原优化问题分为上下2层分别设计,上层选择离散变量,下层搜索连续变量。离散变量的选取需要下层优化目标的函数值,进而给出优化的离散变量的值。

图5 混合参数分层式设计框架
2.1.3 NSGA-Ⅱ求解
NSGA-Ⅱ(non-domination sorting genetic algorithm)是一款增加了快速非优超排序机制的多目标优化遗传算法包[21],本文利用该算法进行连续变量多目标优化搜索。避开Van-Allen内带中粒子密集处,假设波束半张角不大于45°,为严格保证J1=η=1,设轨道倾角i=90°。
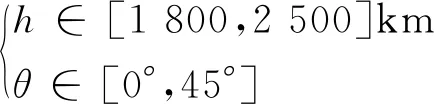
(26)
取Walker星座N/P分别为:48/12,48/16和50/10对应J2和J3的Pareto解集如图6所示。

图6 Walker星座Pareto解集
可见,Walker星座时间分辨率与轨道面数和面内卫星数都相关。当卫星总数相同或接近时,同一个轨道面内卫星颗数越多,则时间分辨率指标越低,观测越频繁;否则,轨道面数越多,空间分辨率指标越低,观测信息越精确。当N/P=50/10时,无论F取什么值,所有卫星任何时刻都存在4条星间链路可能,J4=nisl=4。当轨道高度已知后,面内卫星数不满足(13)式,则J4=nisl=2。星座部署代价如(14)式和(15)式所示,具体指标随航天市场变化,本文不深入调研。
2.2 低轨星座设计
2.2.1 设计模型
相比较中轨电子侦察星座而言,低轨光学卫星星座高度一般在630~650 km之间,且采用太阳同步圆轨道,升交点赤经和相位满足观测区域地方时要求。除此之外,还需考虑光学卫星对地覆盖仰角ε,如图7所示。

(27)

(28)


(29)
进一步,若波束半张角因光学卫星镜头标准化等约束出厂即给定,则轨道高度h成为决定地面分辨率的唯一参数。可见,低轨星座只需设计轨道高度和“并肩扫推”卫星环组数即可。后者直接可以计算星座部署成本和白天观测时间分辨率。

图7 光学卫星对地观测几何关系
2.2.2 中低轨间链路
若低轨光学卫星轨道高度取极限情况hl=650 km,根据(13)式,中低轨星间链路存在的条件中,需更新地球半径Re为(Re+hl)。若N/P=50/10时,轨道面内5颗卫星,需轨道高度hm>1 659.118 km,则中低轨间存在“永久”星间链路几何可能。
2.3 中低轨混合星座算例
优先考虑轨道回归特性,中轨Walker星座取图6中N/P: 50/10 Pareto解集中h=2 165.6 km,θ=
0.137 97 rad。
考虑中轨卫星可能携带光学载荷,考虑太阳同步轨道倾角i=1.849 53 rad,则J1=95.11%,J2=7 318.8 s,J3=300 km,J4=4。并取F=1。以索马里海湾为假设详细查看目标,取太阳同步轨道高度为645.151 km,每天飞行14.75圈,1组4颗卫星“并肩扫推”。则中低轨混合星座如图8所示。
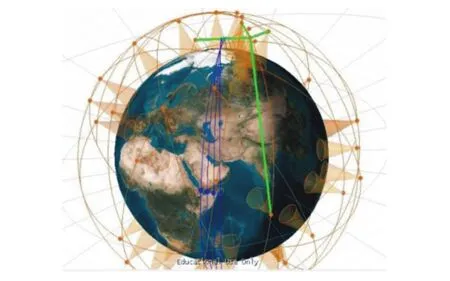
图8 中低轨混合星座星间链路
3 高低轨混合星座
3.1 高轨星座的设计
高轨指轨道高度大于Van-Allen带外带(约25 000 km)高度以上的轨道。早在1945年,Clarke指出在地球静止轨道上等相位间隔放置3颗卫星,就可以实现全球两极以外的覆盖,地球静止轨道卫星高度h=35 786 km,设计变量为卫星个数、波束半张角、定点经度。
3.2 高低轨混合星座算例
当高轨卫星个数为3时,保证赤道全覆盖波束半张角为8.05°,分别定点112°E,-128°W和-8°W,则全球覆盖率J1=74.392%;覆盖区域时间分辨J2=0,未覆盖区域时间分辨率J2=∞;高轨卫星空间分辨率较低,取决于载荷功能,以地球静止轨道构成的星间链路可以对低轨卫星全天候覆盖。为提高地面全球覆盖率,在保证同等空间分辨率情况下,增大覆盖幅宽成本会显著提高,也可以通过增加卫星数量弥补。当高轨卫星个数为4时,波束半张角仍为8.05°,分别定点22°E,112°E,-68°W和-158°W,则全球覆盖率增大J1=82.7%,部署成本增大。
4 结 论
本文提出了对地观测混合星座性能指标、约束条件和多目标优化设计方法,验证算例表明:混合星座可以同时满足对地观测多种性能指标要求;分层多目标优化能有效求解混合星座Pareto解集,便于方案论证和择优;利用中低轨混合星座和高低轨混合星座均可达到基本设计目标。初步分析:中低轨混合星座需要卫星数量较多,抵抗卫星失效能力强,星间链路距离较短,便于低功率数传;而高低轨混合星座卫星数量少,需要较高的数传功率;中低轨混合星座和高低轨混合星座优劣性还需进一步调研商业卫星、载荷和航天发射部署成本,补充完善成本函数具体数值后进一步计算比较。
