基于三维霍夫变换的环形光场三维重建

宋征玺, 吴淇, 王雪, 王庆

(西北工业大学 计算机学院, 陕西 西安 710072)

三维重建是计算机视觉领域的经典问题之一,旨在通过多幅图像间特征关联计算目标的三维信息。在基于图像的三维重建方法中,具代表性的SFM[1]与SLAM[2-3]方法已经广泛应用于室外大场景稀疏重建。由于图像中特征点间关联缺乏有效的先验,特征点间的相似性干扰特征匹配、三维点云与相机姿态捆绑调整等步骤,制约了多视图三维重建方法运算速度与精度。光场成像技术通过高维的数据采集模式,能够记录不同角度的光线强度并有助于提升视觉系统感知场景及目标深度的性能。

Levoy等[4]提出平行双平面模型并能够实现对空间光线四维信号(空间和角度)的有效采集。通过空间-角度维组合,视觉特征在对极平面图(epipolar plane image,EPI)[5-6]中呈现一致性分布。当视差范围小于(±1)时,一致性特征为连续的直线且斜率与目标深度相关。但双平面光场仅能获得2.5D的目标重建,难以实现360°目标重建。

将相机环绕旋转轴等间隔采样可获得环形光场,该三维图像体记录了场景与目标3600光线强度。视觉一致性特征具有高维连续光强分布特性,且光强分布轨迹蕴含了场景及目标与相机的相对运动关系。随着采样密度的增加,光强连续分布的一致特性不断增强。Feldmann等[7-9]提出了环形光场中特征轨迹分析方法(image cub trajectory,ICT)。Yucer等[10]通过研究高角度分辨率采集(10帧1°),在二维EPI中通过局部梯度计算目标深度。Vianello等[11]在二维EPI上进行线检测,利用二维霍夫变换求解曲线参数并进行深度估计。此方法在正交投影模型下,可以准确估计场景深度。但在摄影投影下,图像体特征轨迹分布在多层EPI中,并呈现三维分布特性。因此,二维霍夫线检测难以解决一致性视觉特征轨迹不完整引起的曲线参数估计歧义性。基于特征轨迹呈现三维分布的特性,本文提出基于三维霍夫变换的环形光场三维重建算法。根据环形光场空间和角度采样分辨率,本文定义了高维霍夫空间,并采用三维结构张量分析特征轨迹局部方向,以解决二维霍夫变换估计三维曲线参数的歧义性。本文构建了环形光场仿真与真实数据集,通过定量与定性分析验证了算法的有效性。

1 环形光场数学模型

设目标旋转中心为M,相机焦距是f,光心坐标为C(xc,yc),相机与旋转轴距离为RM。三维空间中一点P,到旋转轴距离为R,初始相位为φ,如图1a)所示。在X-Z世界坐标系平面上,X,Z分量可以通过极坐标表示

X=Rsin(θ+φ)

Z=RM-Rcos(θ+φ)

(1)

在旋转角度θ∈(0～2π]中依次采集的图像构成三维图像体V(x,y,θ),特征点轨迹曲线为(2)式所示

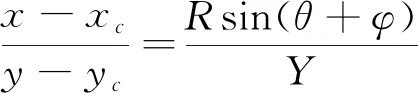
(2)

其在x,y方向投影分别如(3)至(4)式所示

(3)

(4)

环形光场一致性特征分布为三维空间中的正弦曲线。图1a)空间中P1,P2,P3点,其旋转半径分别为R1,R2,R3,其初始相位分别为φ1,φ2,φ3.其在三维图像体中的特征轨迹如图1b)所示。随着空间点距离旋转轴半径R增大,曲线的振幅随之增大。由于点P2在摄像机的水平视线平面上,即曲线完整分布在y=yc平面上,其余空间高度下特征点的轨迹均为三维曲线,即其分布在[y′-Δy,y′+Δy]的图像体中。

图1 环形光场采集模型与三维图像体空间特征轨迹示意

2 基于三维霍夫变换的三维重建

霍夫变换广泛应用于图像分析中直线以及二次曲线的参数估计。在相机摄影投影下,一致性特征轨迹分布在多层EPI中。本文引入三维结构张量分析高维曲线局部方向,并设计三维霍夫空间进行曲线参数求解。霍夫变换需要在二值图像中提取检测点,因此本文采用3D Canny算子提取图像体中的V(x,y,θ)三维曲线。

2.1 基于三维结构张量的参数求解

通过3D Canny算子得到图像体中高维曲线E(x,y,θ),已知曲线中的点x,y,θ,而需求解的曲线参数为(R,φ,Y)。根据(2)式,当已知部分参数R,Y时,φ具有2个解。但2个解所处的曲线方向不同,因此可采用结构张量分析图像体的局部方向。将三维图像体V(x,y,θ)分别对x,y,θ求偏导得到V=(Vx,Vy,Vθ)T,则其三维结构张量表示为

(5)

根据三维结构张量定义可知,三维结构张量的局部特征方向在y=y*平面投影与x轴的角度为[12]

(6)

正弦曲线是周期函数,其φ+θ解分布在Ⅰ、Ⅱ、Ⅲ、Ⅳ 4个区域。根据(6)式,可唯一确定参数φ,即

(7)

2.2 三维霍夫空间

三维霍夫空间由参数H(R,φ,Y)定义,参数空间的每一组取值表示图像体中的一条三维曲线E(x,y,θ)。根据传感器尺寸与环形光场采样数量将三维霍夫空间离散化三维网格,每个网格初值为零。设传感器尺寸为Nx×Ny,单个像素的物理尺寸为s,则点云的旋转半径R与曲线幅值的关系为[9]

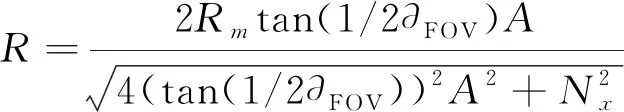
(8)

式中,∂FOV=2arctan((s·Nx)/2f),A∈[0,1,…,Nx/2]。

三维霍夫空间Y的离散化采样与Ny相关

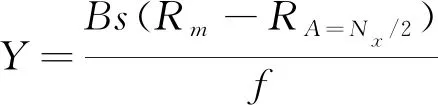
(9)

式中,B∈[0,1,…,Ny]。

参数φ离散化为环形光场采样帧数N,则

(10)

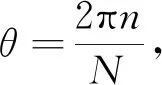
令3D Canny点云中一点E(xi,yi,θi),遍历A中每一个值,根据(3)式,φ有2个解φ+和φ-,可根据其局部方向确定唯一解(见(7)式)。此后,依据(4)式,计算得到Y。在3D Canny点云中所有点参与投票后,对应的参数空间依次累计得到局部最大值,即为特征轨迹曲线对应参数。

2.3 三维曲线参数筛选策略

真实空间中的物体以不同的半径绕轴旋转,其对应的图像体空间中的三维正弦曲线有不同的幅值。因此,在3D Canny点云中,不同幅值的曲线包含不同数量的点云:旋转半径较小的空间点,其图像体空间曲线的特征点数量较少;旋转半径较大的空间点,其图像体空间曲线的特征点数量较多,即环形光场的采样不均衡。因此在霍夫空间中,对于较大的A区域的累计值将高于A较小的区域。其次,幅值较大的轨迹中的二值点参与投票的次数将多余半径较小的点,因此在霍夫空间中噪声在A较大的区域较大。

首先采用低通滤波器对霍夫空间的低频区域进行滤除。然后设计与霍夫空间等尺寸的三维权值矩阵W(A,B,γ),其A维每一列为e-0.001·[1,2,…,Nx/2]T。通过将权值矩阵点乘霍夫空间的方式进行标准化处理。此时,可采用全局阈值(Otsu算法)确定空间中的所有局部最大值。原始霍夫三维空间以及标准化霍夫空间如图2所示。

图2 三维霍夫空间

3 环形光场三维重建算法

基于三维霍夫变换的环形光场三维重建算法的流程如表1所示,该算法的输入是环形光场高维图像体,输出是三维点云。

表1 算法流程

4 实验结果与分析

为了验证本文算法的有效性,分别对比了3种三维重建算法：①Geosele等人提出的多视立体重建(multi-view estimation,MVE)[13]；②Furukawa等人提出的基于聚类的多视图立体重建(clustering views for multi-view stereo,CMVS)[16]；③Vianello等人提出的基于二维霍夫变换的环形光场重建方法(2D Hough)[11]。

4.1 三维霍夫变换性能分析

本文采用Blender[14]仿真生成了环形光场数据集,所有数据集中包含720个视点,每个子视点下图像大小为960×540,像素的尺寸为6 μm。为验证三维霍夫变换的性能,对全局阈值分别取[0.1,0.9]增量为0.1,对比二维霍夫变换与三维霍夫变换生成点云数量与均方根误差(RMSE)[15],如图3所示。随着全局阈值的增大,无论二维、三维霍夫其点云数量不断减小,RMSE不断减小。在相同的阈值下,三维霍夫重建得到的点云数量多于二维霍夫重建方法,且误差普遍较小。

图3 3D/2D霍夫变换性能对比

4.2 仿真数据结果

图4展示了4种方法在2组不同数据集中的重建效果,表2给出了重建误差RMSE。这两组数据有大量的相似性特征,在佛像数据中,物体表面纹理较为相似且具有一定的镜面反射。MVE算法重建的结果具有较多的噪声,CMVS算法仅能够得到SFM的结果,由于点云过于稀疏难以得到稠密重建的结果。整体基于环形光场霍夫线检测的算法优于多视图算法,但由于二维霍夫变换难以对三维曲线参数进行有效的解算,其在目标上下边缘区域误差较大。且在佛像平滑的面部区域,估计出现较大的空洞。而三维霍夫重建方法能够得到较为完整与精确的估计,其RMSE为4种方法最小。在树枝数据中,目标呈现朗博特性且相似性特征较多。MVE算法无法对此类目标进行三维重建,而CMVS算法收敛至2个目标,整体误差较大。基于三维霍夫重建的方法在目标的凹面,遮挡关系较为复杂的区域能够得到较好的估计结果。

图4 仿真数据对比效果

4.3 真实数据结果

采用NIKON D700相机采集环形光场的图像分辨率为4 256×2 832,每个传感器尺寸为8.4 μm,焦距为f=48 mm。目标放置在高精度的旋转台,共采集360帧图像(角度分辨率为1°)。采集2组数据进行三维重建实验,真实场景采集数据包含复杂的图像噪声、光照变化等,如图5所示。由于相似性的特征导致多视图重建方法难以得到有效的三维重建结果,MVE算法无法得到点云,而CMVS算法估计得到的点云不收敛。基于霍夫检测的三维重建方法整体优于多视图的算法,本文提出的三维霍夫重建方法能够得到更多细节。与2D Hough算法相比,本文可以在目标的上下边缘处较好的估计三维点云,且点云更为稠密,如图5所示。CMVS与MVE等方法在目标有大量相似特征时,出现重建失效或结果过于稀疏的现象。

图5 真实数据对比效果

从计算复杂度看,二维霍夫变换是逐层(图像垂直方向)对EPI图像进行Canny边缘提取,并进行霍夫计算。而基于三维霍夫变换是对整个图像体进行霍夫计算,从霍夫计算这一步看从二维到三维没有增加运算量。但由于一致性视觉特征具有三维分布特性,因此采用3D Canny会比2D Canny得到更多的边缘特征点,如图4至5所示。因此,三维霍夫变换比二维方法,运算时间更长但得到更加密集的重建效果。

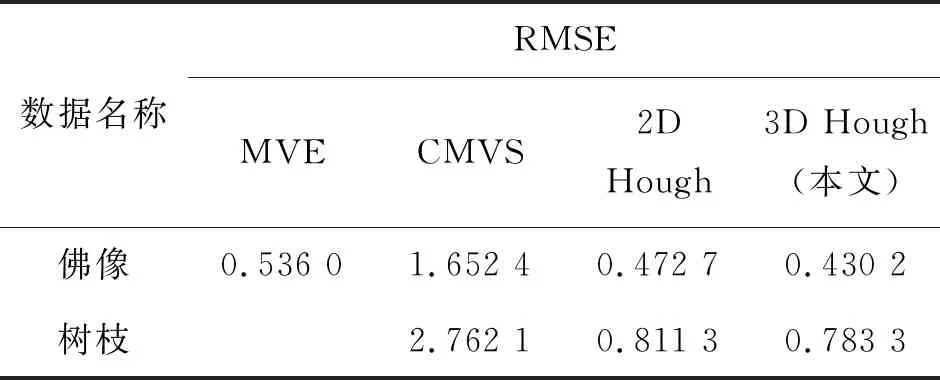
表2 RMSE均方误差对比

5 结 论

根据环形光场特征轨迹呈现三维分布的特性,本文提出基于三维霍夫变换的环形光场三维重建方法。本文通过分析特征轨迹三维分布,采用3D Canny算子提取图像体中的轨迹曲线,并采用三维结构张量分析曲线的局部方向。构建面向三维曲线检测的三维霍夫空间,设计了霍夫参数筛选方法。通过曲线参数恢复每个视点下的深度图,生成每个视点下三维点云并通过环形光场系统参数融合最终得到重建结果。本文在环形光场仿真与真实数据集中进行了三维重建实验。结果表明,该方法能够提高重建的精度与效果。