基于线性残差变系数模型的哈尔滨房价研究

高明明， 曹连英

(东北林业大学 理学院，哈尔滨 150036)

由Hastie T和Tibshirani R[1]提出的变系数模型是近期发展起来的一类非常重要的非参数回归模型，模型中的回归系数是其他协变量(如时间或空间)的未知函数，即模型考虑了影响因素对响应变量在时间或空间上呈现的差异性，从而与线性模型相比变系数模型具有更强的适应性，受到了国内外学者的关注，变系数模型的局部多项式估计[2]、局部加权最小二乘估计[3]、Bayes样条估计[4]等估计方法和理论[5]被相继提出.在光滑参数的选择方面，除了普遍应用的交叉验证法、BIC法、AICc等选参准则，吕晓玲等[6]提出将ESCV方法应用到变系数模型，以保证模型的稳定性.此外，变系数模型在经济学、统计学等诸多领域也被广泛应用：朱青等[7]构建了变系数面板模型以验证中国各省市区收入差距对经济增长的影响；为提高预测效果，舒通[8]采用变系数回归模型对WTI原油的季度平均价格进行预测，指出相比于常系数模型，变系数模型在提高拟合精度和预测精度方面更具优势；王艳[9]对黄金价格及其影响因素的关系进行了定量分析，并基于黄金样本数据对比线性回归模型与变系数模型的残差值和误差率，发现变系数模型预测结果更精准；甘胜进[10]基于变系数模型对苏州房价与平均工资、人口数之间的关系进行了研究，并与线性模型进行比较，结果表明：变系数模型明显优于线性模型.刘锋等[11]考虑了时间对重庆市房价的差异性影响，利用变系数回归模型拟合房价数据，并与线性回归模型的拟合效果进行对比分析，得出变系数模型拟合效果更佳的结论.

前人研究工作表明：线性模型具有良好的解释性和外延性，但自适应性弱，拟合和预测效果欠佳；变系数模型的拟合和预测精准性较强，但解释能力和外延性较弱.在应用模型解决实际问题时，不仅要求模型具有较高的拟合和预测能力，也注重模型中变量对问题的解释性与和模型的外延性.为解决这一类矛盾，本文给出分段解决方法：先建立显著的线性模型，然后基于线性模型的残差建立其余相关影响因素的变系数模型，从而在保持模型良好的解释性和外延性的同时，提高模型的拟合和预测精度.

哈尔滨作为东北北部地区的经济、政治、文化中心，其房地产市场越来越旺盛，因此房价的变化及其影响因素备受瞩目.杨晓东[12]基于哈尔滨市房价收入比情况研究哈尔滨市房价走势，并预测哈尔滨市未来几年的房价.何玲[13]从供应、需求、综合三层面分析了哈市商品住宅价格的影响因素并采用5次多项式模型对哈市房价的走势进行预测.张博[14]等基于空间地理加权回归构建哈尔滨商品房房价模型,讨论分析哈尔滨房价空间差异性的影响因素.

本文基于哈尔滨市(包含九区三县两市)2000～2017年的住宅商品房平均销售价格等数据，阐述一类问题的解决方法，同时在宏观角度上，利用相关数据结果对哈尔滨市平均住宅商品房房价的趋势进行分析，指出了影响哈尔滨市平均住宅商品房房价的主次要因素，对哈尔滨市房地产整体评估提供了一些参考，也从侧面反映了哈尔滨市房地产市场宏观的发展水平.

1 变系数模型

模型基本形式为：

Y=β1(t)x1+β2(t)x2+…+βp(t)xp+η，

其中：t表示观测数据的时间特征或空间特征，βj(·),j=0,1,…,p为未知系数函数，η为误差项，满足E(η|t,X1,…,Xp)=0,Var(η|t,X1,…,Xp)=σ2,(Yi,Xi1,…,Xip,ti),i=1,…,n为观测值，则样本形式为

Yi=β1(ti)Xi1+β2(ti)Xi2+…+βp(ti)Xip+ηi,i=1…n.

设K(t)为高斯核函数，令Kh0(t)=K(t/h0)/h0，其中h0为光滑参数，

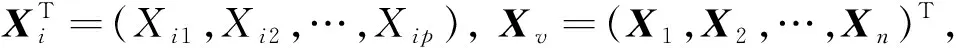
则系数函数向量β(t)=(β1(t),…,βp(t))T，β′(t)=(β′1(t),…,β′p(t))T在t0处的局部线性估计为

(XT(t0)W(t0)X(t0))-1XT(t0)W(t0)Y

则有Y在ti,i=1,2,…,n处的拟合值为：

Li(ti)Y

其中：

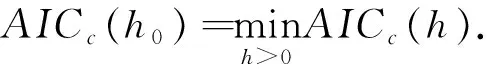
2 哈尔滨市房价分析

2.1 变量选取

本文使用哈尔滨市2000～2017年城镇住宅商品房数据(表1)，住宅商品房平均销售价格、房地产开发住宅投资、住宅竣工房屋面积数据来源于《中国统计年鉴》，城镇居民人均可支配收入和年末城镇人口、商品零售价格指数数据来源于《哈尔滨统计年鉴》(统计年鉴中的最新数据截止至2017年).其中响应变量为住宅商品房平均销售价格(元·m-2)，需求因素选用城镇居民人均可支配收入(百元)和年末城镇人口(万人)，供给因素选用房地产开发住宅投资(亿元)和住宅竣工房屋面积(104m2).本文选用商品零售价格指数(2000年为100)部分消除通货膨胀因素的影响，得到住宅商品房房价及其影响因素的数据.缺失数据(用※标明)取上下年数据的平均值.

表1 哈尔滨市2000～2017年城镇住宅商品房相关数据

2.2 模型建立

首先对经过处理的房价及其影响变量数据作相关性分析，结果表明：住宅商品房平均销售价格与城镇居民人均可支配收入、房地产开发住宅投资、住宅竣工房屋面积、年末城镇人口存在相关性，而且自变量间也有一定程度的相关性，为了简化变量、消除变量间的多重共线性，本文利用逐步回归的方法先对变量进行筛选，建立多元线性回归模型.如表2所示，住宅商品房房价与城镇居民人均可支配收入X1、房地产开发住宅投资X2具有显著的相关性.

表2 线性模型汇总

基于逐步回归的多元线性回归模型为：Y=1 183.844+12.366X1+2.336X2+ε多元线性回归模型的真实值与拟合值对比图如图1(A).应用多元线性回归模型估计出消除通货膨胀后2017年哈尔滨市的住宅商品房平均销售价格为5 441.6元；换算得到未消除通货膨胀2017年哈尔滨市的住宅商品房平均销售价格为6 546.2元，相对于2017年房价7 861元偏差为16.7%.

为了提高模型的拟合和预测精度，本文亦建立了变系数模型.

Y=α0(t)+α1(t)X1+α2(t)X2+ζ

其中：ζ为误差.变系数模型的真实值与拟合值对比图见图1(B).对比结果表明变系数模型的拟合效果优于线性模型；应用变系数模型估计出消除通货膨胀后2017年哈尔滨市的住宅商品房平均销售价格为7 023.9元，换算得到未消除通货膨胀2017年哈尔滨市的住宅商品房平均销售价格为8 449.7元，相对于2017年房价7 861元偏差为7.49%，即变系数模型预测结果也优于线性模型；但该模型对实际问题的解释有矛盾之处，诸如截距项a0(t)为负值(图2).

由于线性模型的拟合性欠佳，残差非正态分布，见图3，本文基于多元线性回归模型残差项建立其余相关变量的变系数模型.令线性模型的残差为ε，记

εi=Yi-1 183.544-12.366Xi1-2.336Xi2，

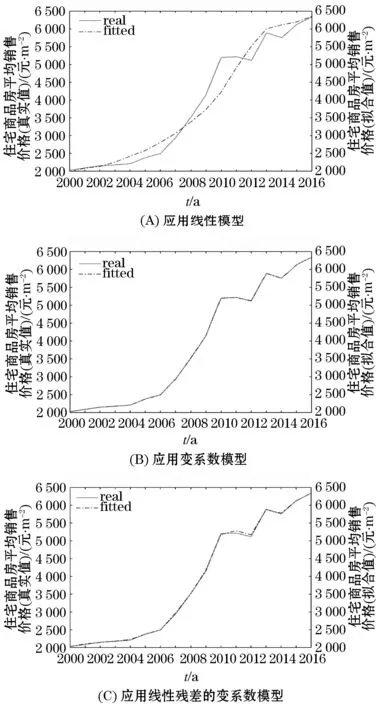
图1 房价的真实值与拟合值对比Figure 1 Comparison of the real value and the fitted value of the housing price

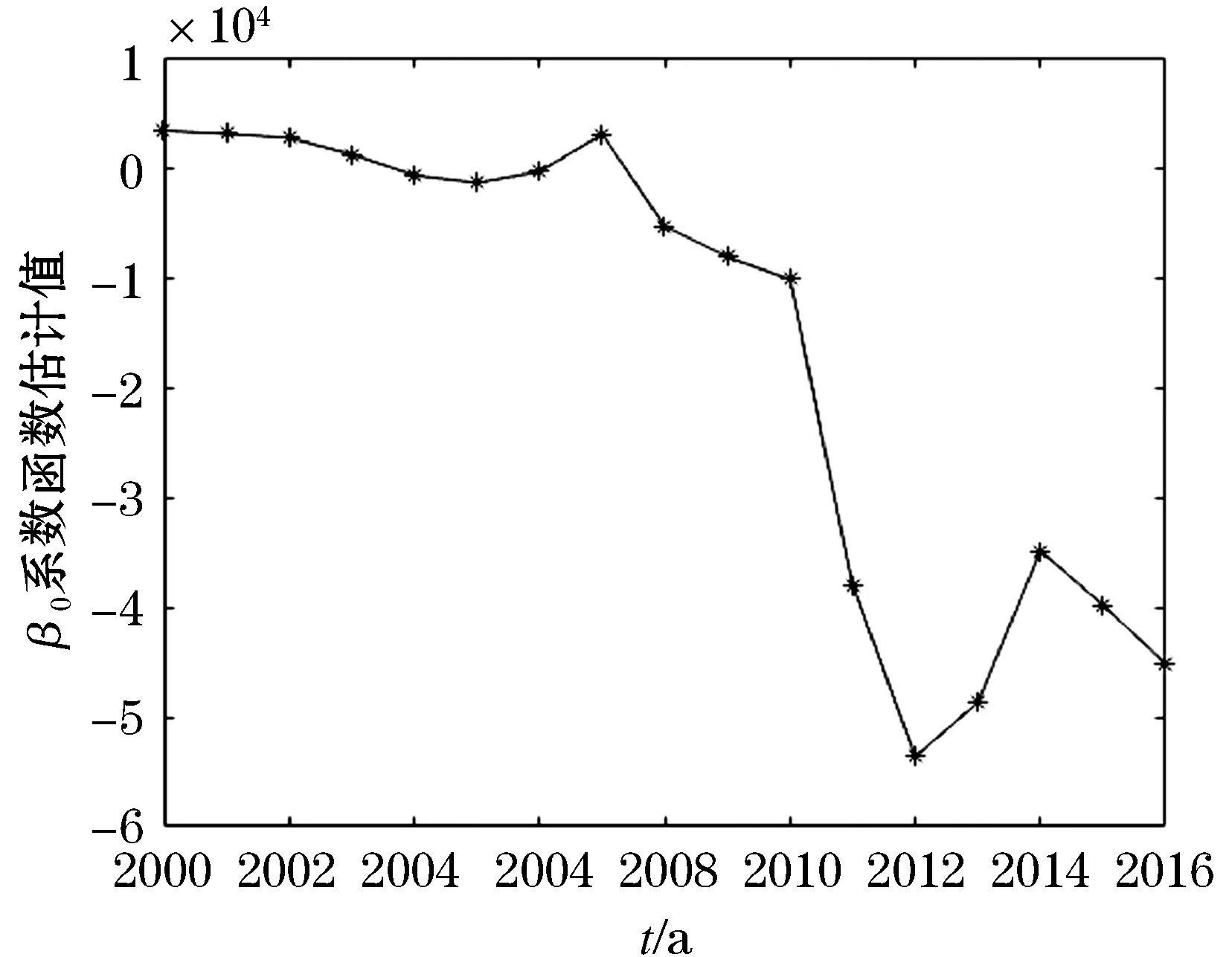
图2 变系数模型中截距项α0(t)Figure 2 Intercept term in the variable coefficient model

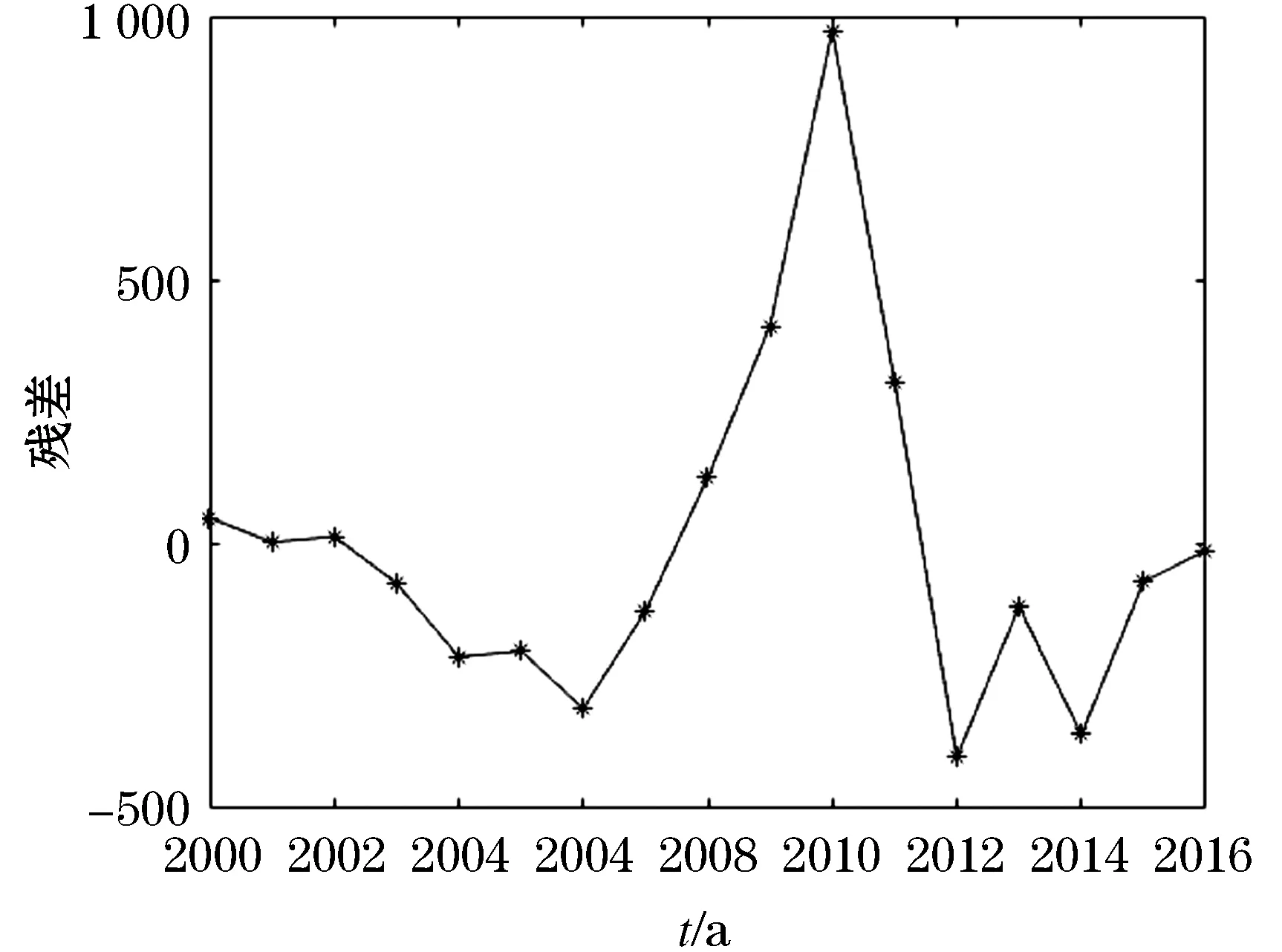
图3 线性模型残差图Figure 3 Residual figure of the linear model

建立线性模型残差ε的变系数模型，

ε=β1(t)Z1+β2(t)Z2+η

其中：Z1为住宅竣工房屋面积(104m2),Z2为年末城镇人口(万人)，η为变系数模型误差.记(εi,Zi1,Zi2,ti)为残差ε、Z1、Z2在ti年的对应值，则残差ε的变系数模型样本形式为

εi=β1(ti)Zi1+β2(ti)Zi2+ηi,i=1,…,17

利用本文中第2部分得变系数及其导数的估计为：

(β1(t),β2(t),β′1(t),β′2(t))T=

(ZT(t)Wz(t)Z(t))-1ZT(t)Wz(t)ε

(1)

其中：

Z(t)=(Zv,TZv)，ε=(ε1,…,ε17)T

T=diag(t1-t,…,t17-t)Wz(t)=

diag(Kh(t1-t),…,Kh(t17-t))

Y=1 189.76+12.338X1+2.335X2+β1(t)X3+β2(t)X4+η

(2)

令t=ti由式(1)得到系数函数及导数在ti年估计值，变系数函数趋势图见图4.利用式(2)可得2000～2016年房价的拟合值(趋势图见图1(C))

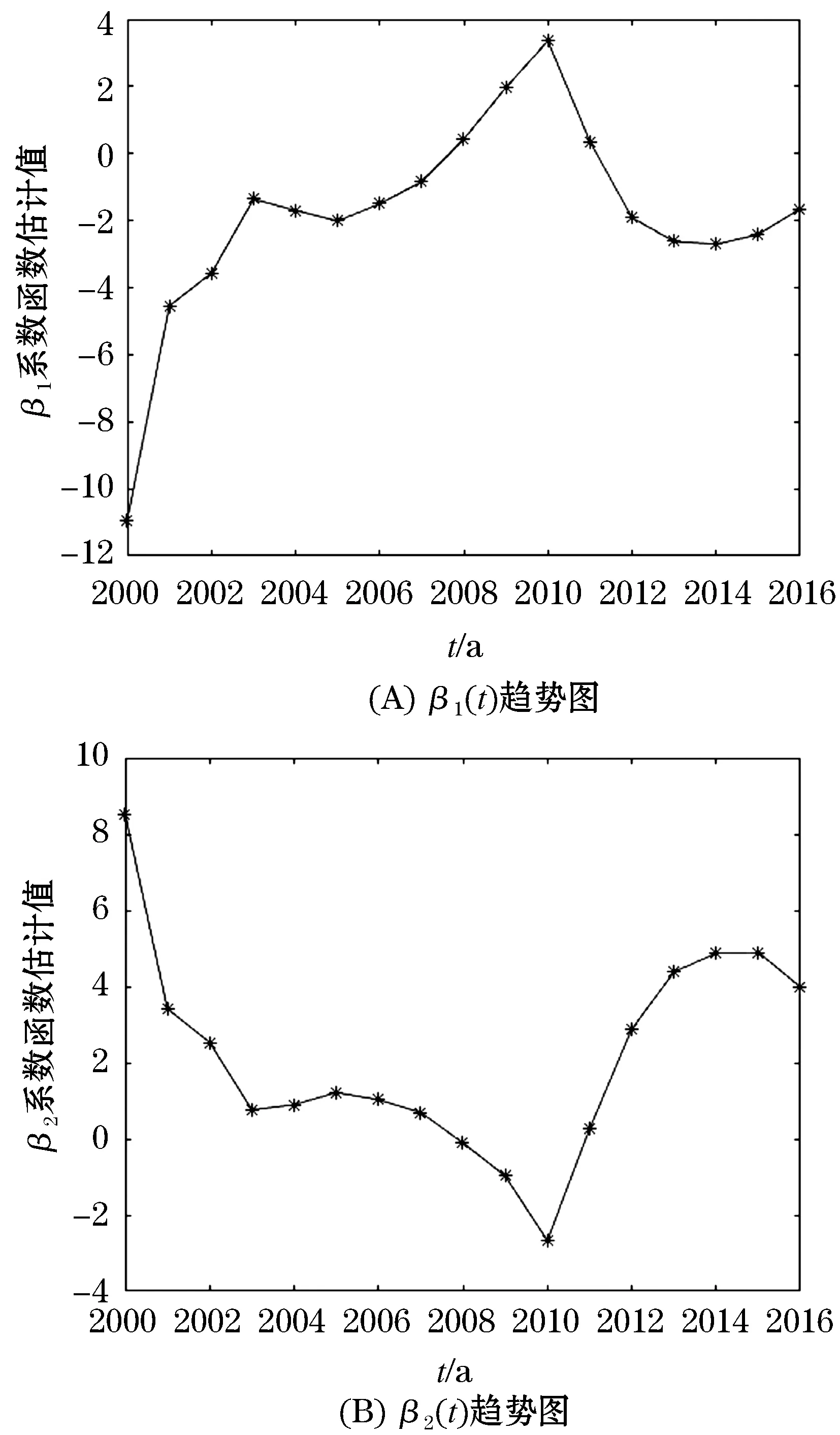
图4 基于线性模型残差的变系数模型中变系数函数趋势图Figure 4 Trend diagram of variable coefficient function in the variable coefficient model based on the residual of linear model

2.3 房价预测

利用分段三次Hermite插值公式

获得2017年(即t=18)的变系数函数估计值β1,18=-0.681 4,β2,18=2.629 7，再利用模型式(2)可预测出消除通货膨胀后2017年哈尔滨市的住宅商品房平均销售价格为6 350.2元，换算得到未消除通货膨胀2017年哈尔滨市的住宅商品房平均销售价格为7 639.3元，相比于2017年房价7 861元偏差为2.82%.

2.4 模型结果分析

相比于多元线性回归模型，基于线性模型残差的变系数模型不仅考虑了城镇居民人均可支配收入和房地产开发住宅投资对住宅商品房平均销售价格的线性影响，同时考虑了住宅竣工房屋面积和城镇人口对住宅商品房平均销售价格的在不同时间上呈现的差异性影响.经相关分析和逐步分析表明：城镇居民人均可支配收入和房地产开发住宅投资是影响住宅商品房房价的主要因素，并且影响关系可描述为线性影响；年末城镇人口和住宅竣工房屋面积是次要因素.城镇居民人均可支配收入对房价产生正向影响，收入增加意味着人们的购买力增强，加之随着生活质量的提高，人们对住房的要求提升，从而住房需求变大，促进房价增长.房地产开发住宅投资是促进房价增长的另一因素，同时房价也对房地产开发投资产生引领作用，房价越高，获利空间就越大，进而房地产商会产生更强的意愿投资房地产.图4(A)均值可以看出，住宅竣工房屋面积对房价的整体影响系数均值是负的，住宅竣工房屋面积增加意味着住宅商品房的存量增大，使得房价下降.图4(B)均值表明，城镇人口对房价整体上呈正向影响，人口的增加会使得住房需求增大，进而促进房价增长.2008～2011期间人口的增加对房价是负影响，这可能受2008年经济危机影响，消费者由于经济等原因对购买房屋处于观望状态所导致.

3 结 语

本文提出分段解决方法，建立了基于线性残差的变系数模型.与单一的线性模型、变系数模型相比，基于线性残差的变系数模型在模型拟合准确度和预测精度上都有很大的优势，并保持了线性模型的解释性和外延性，为研究线性效果欠佳的统计模型问题提供一些参考.基于此模型对哈尔滨市(包含九区三县两市)2000～2016年住宅商品房平均销售价格进行建模，分析了哈尔滨市平均房价的主要影响因素，给出了其他次要影响因素在时间上对哈尔滨市住宅商品房平均销售价格的影响程度的差异性，并对2017年的平均房价进行预测，预测结果表明：2017年哈尔滨市的住宅商品房平均销售价格为7 639.3元，与《中国统计年鉴》中公布的2017年哈尔滨市的住宅商品房平均销售价格相比误差为2.82%.