基于区间模糊相似测度的多属性群决策方法
2021-03-02林志超周礼刚
李 灿,陈 杰,林志超,周礼刚
(安徽大学 数学科学学院,合肥 230601)
随着决策领域的不断发展,多属性群决策问题已经成为现代决策领域中一个重要的分支.在决策过程中,由于决策环境的复杂多变,人们认知的模糊性以及信息表达的不确定性,如何确切的表达决策信息是决策问题研究的关键,虽然直觉模糊集[1]和Pythagorean模糊集[2]已经成为解决决策问题的有效方法,然而它们评价信息的范围有限,因此为了克服这一限制,q阶orthopair模糊集应运而生[3],其中隶属度的q次幂与非隶属度的q次幂之和被限制为1.q阶orthopair模糊集是Pythagorean模糊集的推广,如果q=1,则为直觉模糊集,如果q=2,则为Pythagorean模糊集,即,当q的值越大,更多的q阶orthopair模糊集满足边界限制条件.
由于它在多属性决策问题中的广泛性和高效性,近年来引起了人们的广泛关注,例如Yager[4]研究了q阶orthopair模糊环境的似然性和置信度以及基于拓扑学的广义q阶orthopair模糊集运算法则;Liu和Wang[5]提出了q阶orthopair模糊聚合算子,并将其运用到多属性决策问题;Wei和Gao[6]讨论了q阶orthopair Heronian平均算子及其决策应用; Peng[7]定义了q阶orthopair模糊集的指数运算率和处理多属性决策问题的指数聚合算子.
相似性测度的研究目前广泛的运用在数据分析、机械学习、模式识别等领域,相似测度作为衡量两个属性好坏或线性关系的工具而被应用到普通的模糊集和广义模糊集,如Chiang和Lin[8]构建常规统计模型来推导模糊数据的相似测度,其范围是区间[-1,1];Gerstenkorn和Manko[9]定义了直觉模糊集的相似测度,落在区间[0,1]中;Hung 和 Wu[10]研究了基于质心法的模糊集相似测度;对于区间模糊集,Bustince和Burillo[11]通过两类公式得到了相似测度;此外,相似测度的概念也广泛的运用在广义模糊集和它们的拓展上,Garg[12]讨论的加权Pythagorean模糊集的相似测度,突破了现有的相似距离测度的缺陷,并将其应用到多属性决策问题中.
但基于区间orthopair模糊相似测度的多属性群决策方法目前研究较少,因此在上述研究的基础上,本文构建一种新的区间orthopair模糊相似测度,并基于该相似测度,提出求解群决策中专家权重和属性权重优化模型,最后通过VIKOR方法,结合平均相似测度最大优化模型,将其推广到多属性群决策问题中.
1 预备知识
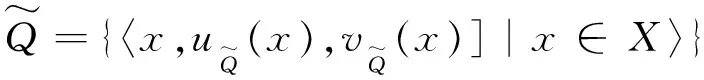





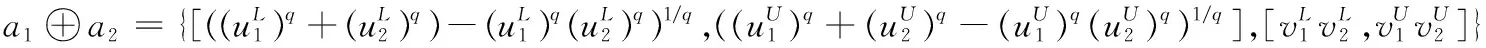
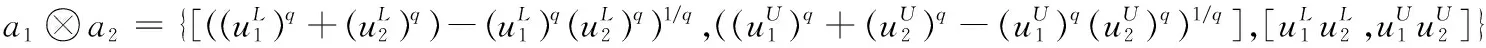
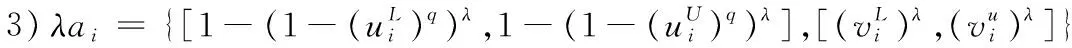

其中:λ>0,q≥1.
文献[14]提出广义区间orthopair模糊加权几何平均算子:
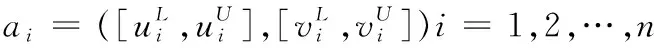
(1)
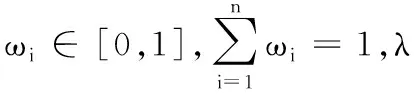
2 一种新的区间orthopair模糊相似测度

(2)
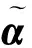
(3)
(4)
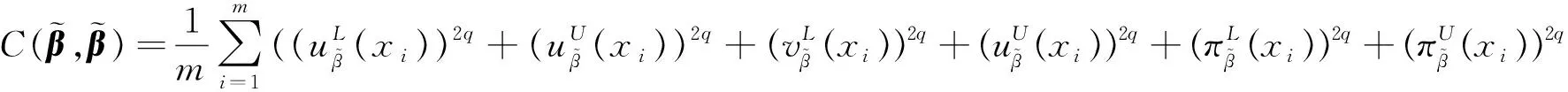
(5)

证明:1)显然成立,下证2)和3).
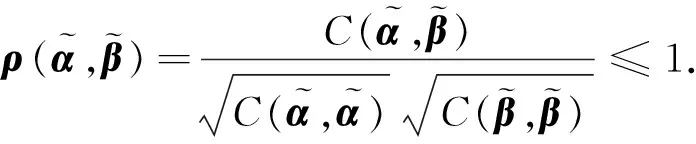
3)充分性显然,结合性质2)的证明,下面证明必要性.根据柯西-施瓦茨不等式[15],
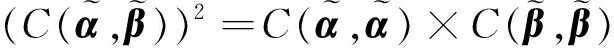
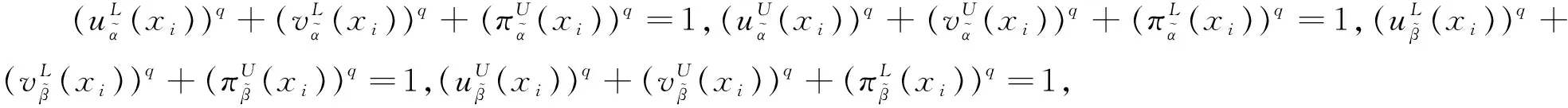
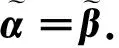
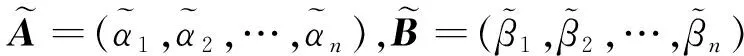
(6)
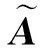
同理,区间orthopair模糊矩阵相似测度满足如下性质:

3 基于区间orthopair模糊相似测度的多属性群决策方法

(7)

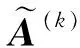
模型(A)
(8)
(9)
(10)
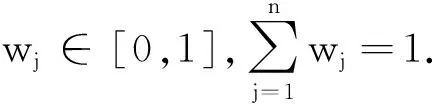
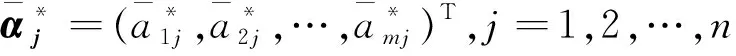
模型(B)
(11)
故有基于区间orthopair模糊相似测度的多属性群决策方法具体步骤如下:
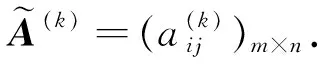

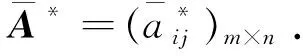
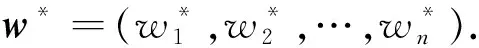
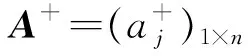
i=1,2,…,m,j=1,2,…n.
(12)
i=1,2,…,m,j=1,2,…n.
(13)
Step 6 在上述计算完成后,根据式(14)~(16)计算各个方案的群体效益值Si、个体遗憾度Ri、折衷值Qi:
i=1,2,…,m,j=1,2,…,n.
(14)
i=1,2,…,m,j=1,2,…,n.
(15)
i=1,2,…,m,j=1,2,…,n
(16)
其中:γ称为决策机制系数,当γ>0.5表示最大化的群体效益值来做出决策;当γ=0.5表示根据均衡折衷的方式来决策;当γ<0.5表示根据最小化遗憾值来做出决策,本文取γ=0.5.
Step 7 分别依据S、R和Q的值由小到大的顺序进行排序,数值越小的方案越优,并确定妥协解.
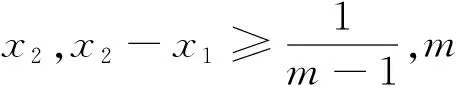
条件2:根据折衷值得到的排在第一的方案x1必须是群体利益值或个体遗憾值排序的最优方案.
如果以上条件有一个不满足,将得到一个折衷解集.
(a)如果不满足条件2,则x1和x2均为折衷解.
4 实例分析
随着时代对于素质教育的提倡,衡量一个大学生优秀与否需从多个方面进考察,而并非仅仅依据文化课成绩.某一学院现需推选一名大学生参与“省三好学生”的评选,目前有五位候选学生xi(i=1,2,…,5),从以下四个方面对这五名大学生进行评价:u1大学期间文化课成绩、u2大学期间公益活动参加情况、u3学生自身特长、u4大学期间获奖情况.现邀请三位老师:e1辅导员、e2系主任、e3院长分别对五名候选学生进行评价.采用本文介绍的方法对五名大学生进行排序,并选出参与“省三好学生”评选的大学生.
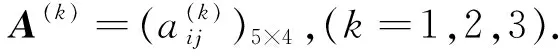

Step 2 取参数q=5,λ=0.5,结合式(7)、(8)求得最优专家权重向量:
ω*=(0.519 4,0.306 0,0.174 6)
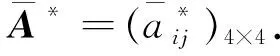

Step 4通过式(10)和式(11)求得最优属性权重向量w*=(0.332 7,0.188 0,0.198 6,0.280 7).
Step 5根据式(12)、(13)结合最优区间orthopair模糊综合决策矩阵,确定各个属性的正负理想方案:
A+=([0.63,0.71],[0.48,0.58]) ([0.70,0.78],[0.45,0.55]) ([0.72,0.81],[0.53,0.64]) ([0.74,0.83],[0.42,0.52])
A-=([0.41,0.49],[0.13,0.22]) ([0.26,0.35],[0.16,0.26]) ([0.24,0.33],[0.25,0.35]) ([0.38,0.46],[0.10,0.20])
Step 6 取参数γ=0.5,根据式(14)~(16)计算群体利益值S和个体遗憾值R,并计算折衷值Q,并依据S、R和Q的值由小到大的顺序进行排序.
如表1所示,S5
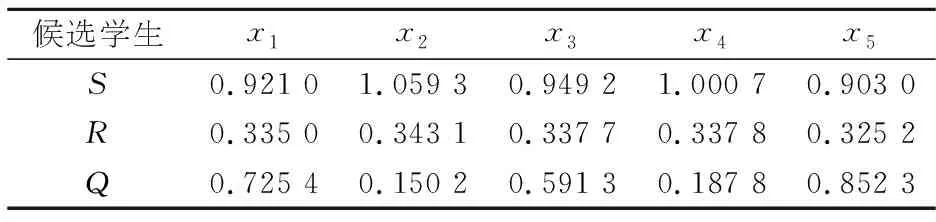
表1 各候选学生的S、R、Q值
下面考虑对参数进行灵敏度分析,为了分析参数q值和参数γ的变化对五名候选学生xi(i=1,2,…,5)的折衷值Q的影响,取参数λ=0.5,考虑q取值从1~20之间变化,γ取值在0~1之间变化,求解结果如图1~5所示.

图1 q和γ对Q1的影响Figure 1 Effects of q and γ on Q1
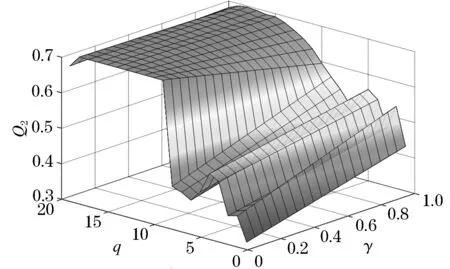
图2 q和γ对Q2的影响Figure 2 Effects of q and γ on Q2

图3 q和γ对Q3的影响Figure 3 Effects of q and γ on Q3

图4 q和γ对Q4的影响Figure 4 Effects of q and γ on Q4

图5 q和γ对Q5的影响Figure 5 Effects of q and γ on Q5
总体看来不同大学生综合素质的折衷值Q受参数q和γ的影响大小不一.由图1所示,随着q的增加,Q1先减少后增加,且在q取13时达到最大值0.8,且受参数γ的影响不显著;由图2所示,在q较小时,随着γ增加,Q2单调增加;由图3所示,随着γ的增加,即决策者注重利益值时,Q3单调减少,且受q影响显著降低,并在q取10以后逐步趋于0;由图4所示,随着q和γ的增加,Q4单调增加,且在q取10时达到最大值1;由图5所示,随着q值的增加,Q5先增加后减少,最后在q取10时达到最大值1,且在q较小时,受参γ数影响显著.
5 结 语
本文提出一种新的区间orthopair模糊相似测度,并讨论其优良性质,进而基于该相似测度构建优化模型求解群决策中专家权重和属性权重,最后提出一种基于区间orthopair模糊相似测度的VIKOR多属性群决策方法,并通过一个大学生学生素质评价案例说明该方法的可行性和有效性,该方法主要特色如下:
1) 用区间orthopair模糊相似测度去衡量相似关系和偏差程度可以有效的减少计算过程中的信息损失,且相似测度考虑到区间orthopair模糊数的隶属度、非隶属度与犹豫度,具有较强的适用性.
2) 本文结合区间orthopair模糊相似测度通过构建平均相似测度最大优化模型求解最优专家权重和最优属性权重,让权重的确定更加客观化.
3) 引入VIKOR方法对备选大学生排序,考虑群体利益值和个体遗憾值选出最佳折衷解,并讨论了参数λ和q的对折衷值Q的影响.
在未来研究中,将进一步对区间orthopair模糊理论和多属性群决策方法做出研究,并将研究结果应用于模式识别、风险投资和医疗诊断等领域.
