一种基于Lattice Boltzmann交通流模型的VANETs连通性研究
2021-03-02李米娜
李 米 娜
(菲亚特克莱斯勒汽车金融有限责任公司,上海 200025)
为了解决交通道路的安全性问题,伴随着无线通信技术的发展,以移动自组织网络(Mobile Ad Hoc Network,MANET)为基础而发展形成的车载自组织网络(Vehicular Ad Hoc Network,VANET)应运而生.VANETs作为智能交通系统ITS(Intelligent Transportation System)的重要组成部分,成为无线通信研究领域的热点,目前得到了国内外研究者越来越多的重视.
车辆相互之间以及和路边基站之间的通信构成车载自组织网络.网络中节点与节点的连通程度决定了整个网络的质量,甚至可以决定这样的自组织网络是否存在[1].目前,有很多关于MANETs节点连通性的研究.例如,P·Gupta和P·R·Kumar(1998年)[2]描述了独立均匀分布的n个节点,将其无线传输范围设为r0=[(logn+c(n))/nπ]1/2,当且仅当c(n)→∞时,无线多跳网络的连通率趋近于1. P·Santi等人(2001年)[3]研究了无线传输范围问题,并得到了节点孤立以及网络一维连通的概率范围.另一方面,L·Wang等人(2008年)[4]研究了一维和二维网络中全连通的节点密度要求.C·Bettstetter于2002年[5]以及2004年[6]研究了最小节点与k-连通之间的关系,并探索了给定节点密度环境下网络全连通的最小无线传输距离r0.
然而,之前的研究在建立交通流模型时,多采用传统的Lighthill-Whitham模型(LW模型).应用传统流体力学方法建立的LW模型中的u-k关系式建立在假设的基础上,而速度-密度关系的假设,是以平衡状态为前提开展的研究,但在实际交通场景中,这种状态可谓是几乎不存在.
本文引入交通流的Lattice Boltzmann模型(LB模型),从而可以避免LW模型中不太合理的u-k关系式[7].通过交通流的LB模型模拟高速公路上车辆的行驶状态,我们得到道路上车流密度,从而推导出自组织网络的连通性.本文提出了一种车载装置无线发射距离的动态调节方法,让车辆以最小的能量来达到VANETs一定的网络连通程度,同时也能达到减少信道阻塞的作用.
1 交通流的Lattice Boltzmann模型建立
本文通过建立交通流的LB模型,来描述车辆在一维交通道路上的情况.定义eα为车辆运动的离散速度向量,表示车辆存在的可能运动状态,表达如下:
(1)
其中:α表示车辆运动的方向:0为车辆静止,1为车辆向前行驶.
在此基础上,我们逐步建立交通流Lattice Boltzmann模型.首先,对应的平衡分布函数形式可设为:
(2)
其中:Aδ,Bδ,Cδ,Dδ为待定系数,这几个参数是根据平衡分布函数所应满足的条件来确定的.δ为车辆运动的状态:0表示静止,1表示运动.然后,依据所需要求解的交通流宏观LW方程[8]:
(3)
其中:k为单行路段上的交通流密度(单位长度的车辆数),u为车流空间平均速度,j为沿着道路的距离坐标,t为时间.考虑到物理学的守恒律,即
(4)
我们可以推导出交通流Lattice Boltzmann模型的平衡分布函数:
(5)
其中:d0,d1,d2为可调的模型参数.相应的控制方程为:
(6)
其中:τ表示松弛时间,fα(x,t)表示t时刻x节点沿离散速度向量eα方向运动的粒子数.宏观物理量为:
(7)
其中:k表示交通流的密度,u表示交通流的速度.
本文用LB方法来模拟交通流,即归结为对方程(6)进行迭代求解,当每一时刻各网格点的粒子分布函数fα(x,t)求出,之后再按式(7)计算宏观力学量.由此可看出,LB算法编程较容易,整个算法可理解为简单的显式迭代过程.
交通流的LB模型的程序流程见图1.
2 车载自组织网络的连通性
上文通过交通流LB模型,可以得到交通道路上各时刻各节点的宏观物理量(速度和密度).本节将从得到的宏观物理量(速度和密度)出发,对道路上车载自组织网络的连通性进行合理的推导.
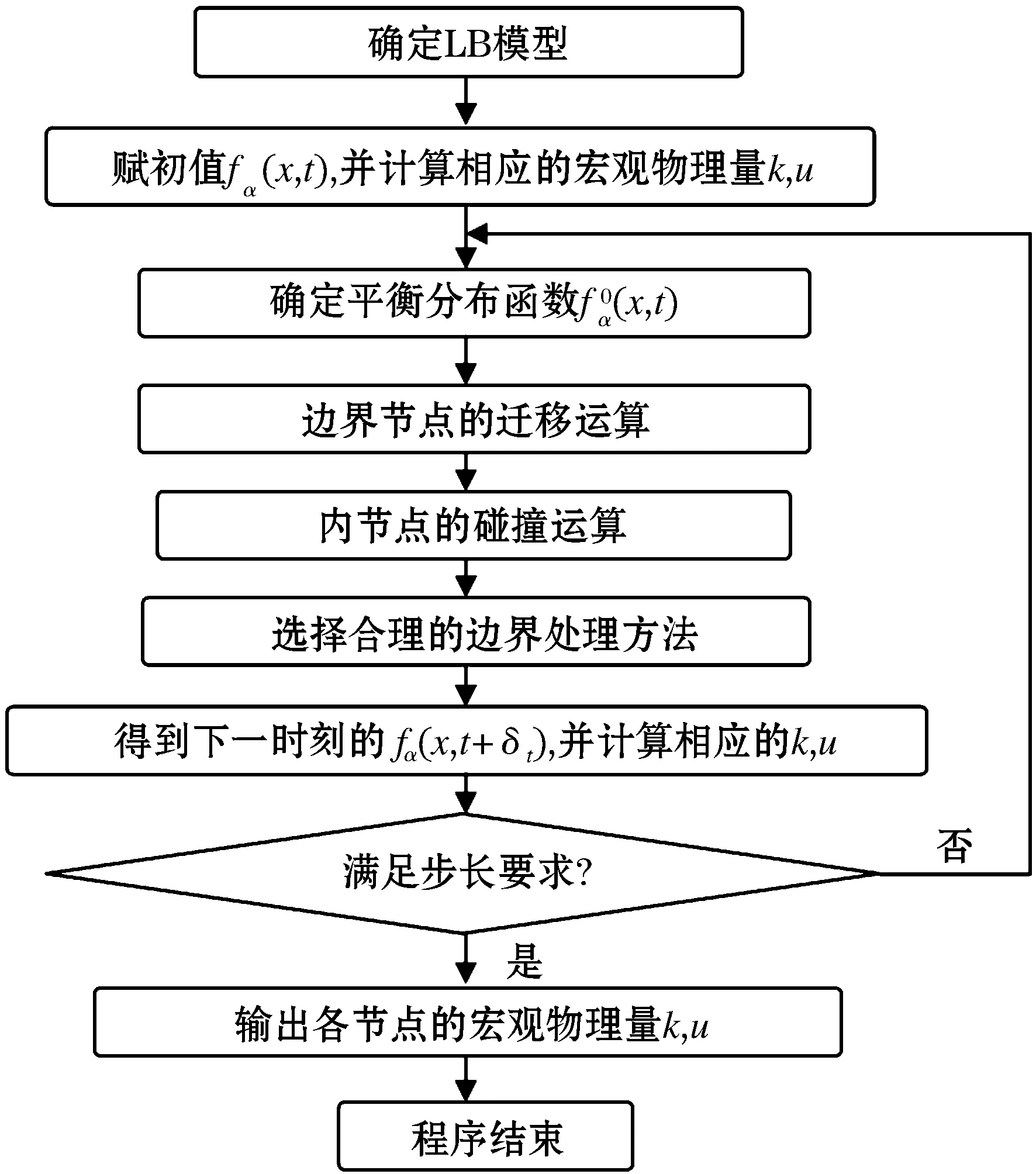
图1 程序流程图Figure 1 Process Flow Chart
首先,假设每辆车都已安装通信设备,该设备以发射距离为r的广播连接模式不断工作,以此来模拟车辆间的无线通信.接着,对如下环节进行定义,如果两辆车之间的欧氏距离小于等于r,表示这两辆车能直接通信(或者称之为连接上了).针对一维自组织网络,可见当一个节点与前方车辆的欧氏距离大于r,则表示没连上,我们称其未能与前面的网络相连(如图2中的节点2).其中“前方车辆”是指所考虑车辆的右边的节点(本文假设交通流从左到右,即车辆前进方向是从左到右的).

图2 一维网络中的不连通情况Figure 2 Disconnected case in one-dimensional network
针对一维网络的情况,我们对其连通性进行定义:当且仅当该一维网络中不存在没能与前方节点接连的任何节点时,网络称为连通的.这意味着,如果该一维网络中存在任意两个距离大于r的相邻节点,此网络就称之为不连通.
接下来,将路段的长度设定为L.为了模型的简化,假设系统达到了一个关于时间稳定的状态,因此所有的变量都与t无关.设N(xa,xb)=N(xa)-N(xb)(其中xb>xa)为区域(xa,xb)的车辆数量.通常情况下,车辆在道路上的分布情况是呈现Poisson分布的[9].至此,我们得到特定数量的车辆处于一段道路区域的概率为:
(8)
其中:
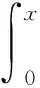
(9)
在时刻t,任意两辆车以间隔时间为I经过该路段,可以得到第i辆车与第i+1辆车的物理间距为:
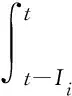
(10)
其中:Ii是指第i辆车与第i+1辆车的到达时距.
在对此网络的连通性考量上,基于以上假设,关键点在于某个到达时距,称之为关键到达时距Tc,这样,如果Ii≤Tc,第i辆车与第i+1辆车在整个行驶过程中始终保持连接.如果Ii
(11)
其中:Ω是指第i辆车与第i+1辆车同时存在于该道路段上的时间点的集合.对于参数为α的Poisson到达过程,P(Ii≤Tc)=1-e-αTc,定义为pc.
基于上述推导,可以得到整条道路网络连通的概率(考虑道路上车辆数量非零,也就是N(L)>0)为:
(12)
其中:E[N(L)]可通过LB模型计算得到,将式(8)代入式(12)中,得:
(13)
3 车载装置发射距离的动态调节
通过对交通流的模拟,我们得到道路上车流信息,然后根据连通性公式,可以计算出道路上的连通性.考虑在长为10 km的高速公路上,道路入口处的车辆到达率为30 veh/min(辆/分钟),车辆以每分钟30辆的频率到达道路入口处,可得到初始密度为0.03 veh/m(辆/米),初始速度为自由速度为60 km/h.根据交通流的LB模型,可计算出道路上的车辆数,根据式(13),在图3中描绘了道路段上网络连通概率关于发射距离r的函数.
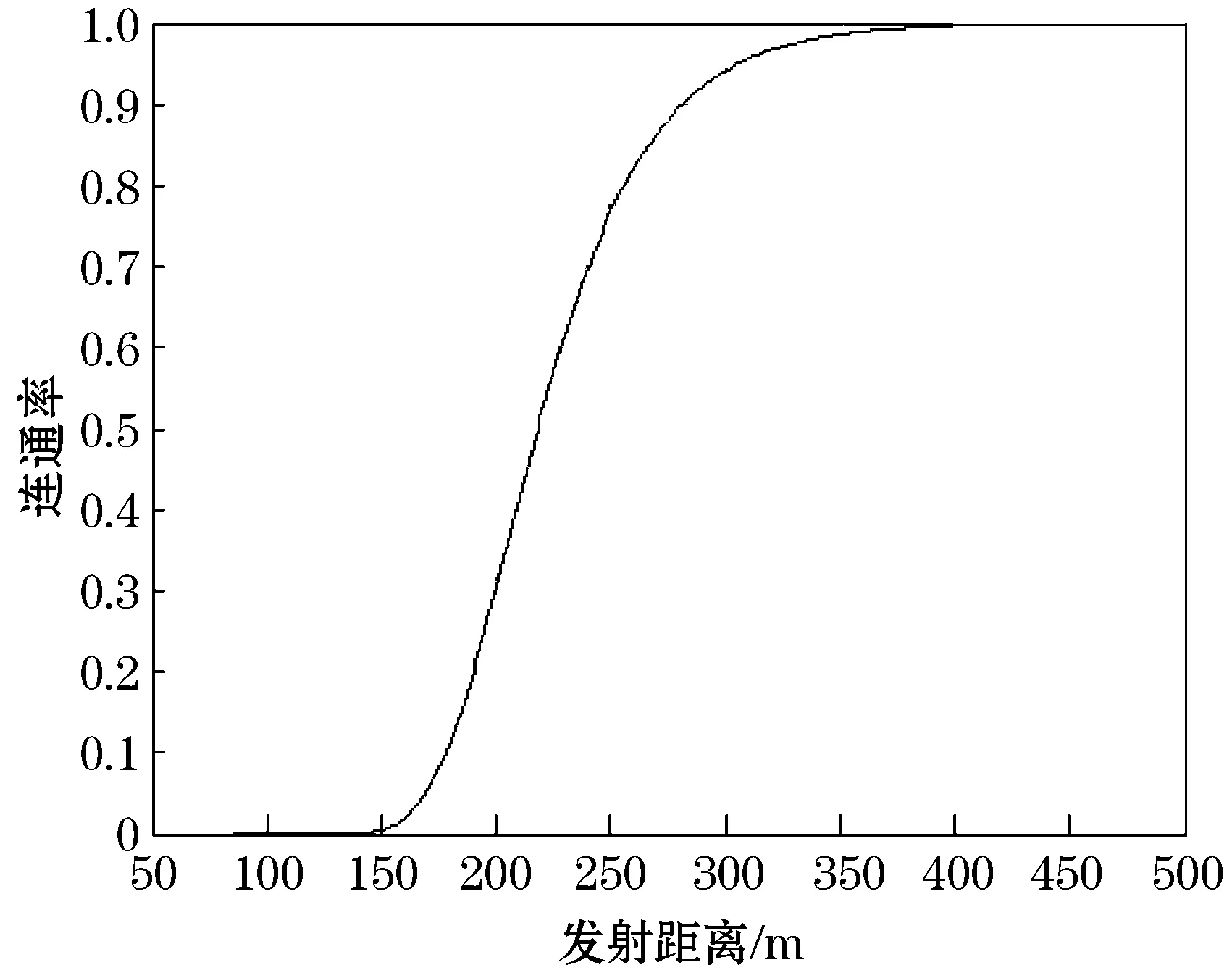
图3 网络连通概率关于发射距离r的函数(α=30 vel/min时)Figure 3 The probability of network connectivity in transmitting distance r(α=30 vel/min)
从图3中可以看出,车辆以30 veh/min的到达率来到路段上,当车辆的发射距离达到400 m以上时,整个网络都可以获得比较好的连通程度.
在实际情况中,对于不同的交通情况,比如上下班高峰时期,道路上车辆密度较大时,即使车辆以较小的发射距离收发信息,整个道路网络依然可以获得较好的连通率;而对于深夜道路车辆稀少时,即使车辆以最大的发射距离收发信息,仍然无法达到网络的连通[10].
考虑当车辆到达率到达44 veh/min时,道路上的车流密度较大,此时的网络连通率与发射距离的关系如图4所示.
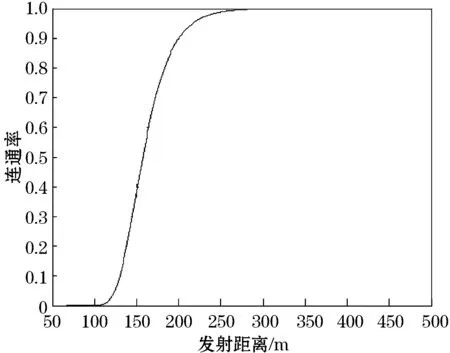
图4 网络连通概率关于发射距离r的函数(α=44 veh/min时)Figure 4 The probability of network connectivity in transmitting distance r(α=44 vel/min)
很明显根据此时的道路状况,车辆只需保持270 m左右的发射距离便可以达到网络的良好连通性.如果在这样的路况下,车辆依旧保持500 m的发射距离,一方面造成了通信费用的浪费,另一方面也会给网络传输信道带来一定的困扰,甚至会造成信道阻塞的可能.
因此我们提出,让车载装置根据不同的道路情况,自行调节发射距离,从而达到避免信道阻塞的风险,也能节省能源.
4 结 语
作为新兴的智能交通网络的重要组成部分,车载自组织网络得到了越来越多研究者的关注.目前关注最多的方面也主要集中于网络的安全方面的研究,其中,网络连通性作为VANETs重要的考虑因素,其研究领域也得到了充分的重视[11-12].
之前相关的连通性研究,在考虑交通流的模拟时,常用传统的交通流模型(如Lightill Whitham模型等),在模拟交通流实际状况时有很多不足之处.本文引入交通流的Lattice Boltzmann模型,从而可以避免建立u-k关系式,由于u-k关系式一开始就建立在假设的基础上,实际交通情况中几乎不存在,几十年来的交通流建模也一直围绕u-k关系式在进行讨论,尽管该模型的合理性已经不断得到改进,但现实中交通道路的情况存在复杂性和多样性,基于该模型的研究还远未达到完善的程度.而本文引入的LB模型不仅可以避免u-k关系式的存在,还能更加准确地捕捉到激波的现象[13].
如今,大多数车辆都装有能收集速度信息的导航系统[14-15].这些信息能作为LB交通模型初始的输入,用于计算车辆密度.在实际操作中,通过给定道路状况的边界值,我们就能得到不同路段上车载自组织网络的连通程度.
本文的模型能在许多领域得到扩展,用于研究更为复杂的交通场景.而连通性的推导,也能用于将来VANETs基站的铺设、交通紧急事故发生时的道路管理以及为车辆传输协议的制定提供参考.
