基于MRF分层高斯混合模型的脑MR图分割

王燕贞，陈志翔，徐镇辉

(1.漳州职业技术学院 信息工程学院，福建 漳州 363000; 2.闽南师范大学 物理与信息工程学院，福建 漳州 363000)

图像分割在医学影像分析中有着广泛应用.由于医学影像灰度不均匀等特点使得分割医学图像存在较大难度.以脑部MR图为例，使用计算机辅助疾病诊断的前提就是要准确地划分脑组织：CSF(脑脊液)、GM(灰质)和WM(白质).准确识别脑组织的变化模式对于疾病早期诊断和检测有着重要的意义.但是由于MR图像中存在噪声和偏移场等，使得医学图像的分割成为了研究的难点和热点.

有限混合模型(FMM)[1-2]作为概率建模工具，能较好地描述图像像素的分布情况，逼近多种复杂分布，因而在计算机视觉和图像识别中得到了广泛应用[3-5].近年来，也有很多学者将混合模型应用于医学图像分析[6-7].特别是高斯混合模型(GMM)[8-10]，由于其简单易实现而备受青睐.Yong Xia等[11]提出基于学习局部变分高斯混合模型的脑MR图像分割算法.该算法将变分贝叶斯推理引入到脑MR图像分割中，同时对该模型进行小数据量训练，并将结果通过线性组合进行分类以达到减轻偏移场影响的效果.2018年赖嘉伟等[12]在传统的高斯混合模型基础上，提出了基于狄利克雷分布和参数分析的GMM-NI模型.该模型利用狄利克雷分布对相邻像素进行处理，选取相邻像素的均值乘以特定系数来代替该范围的像素值，起到了平滑噪声的作用.同时使用梯度下降法降低算法的复杂度.实验证明：GMM-NI算法与FCM、k-均值和传统GMM算法相比，在一定程度上降低了误分率并提高了运算性能.该算法虽然在一定程度上提高了分割精确率，但均值法容易丢失图像细节.柴五一等[13]提出两种基于传统高斯混合模型的改进算法MC_GMM和NI_GMM.MC_GMM算法是对高斯混合模型进行多分类，而NI_GMM则是基于空间约束，即对像素先验概率和条件概率添加空间信息约束，利用像素空间距离和灰度值之间的关系，使用均值模板实现空间约束.试验证明，这两种算法在结构相似性、信噪比等方面要优于以往高斯混合改进算法.MC_GMM由于没有考虑邻域信息，精确率提升的空间有限，而NI_GMM引入了空间约束，优化了分割效果，却加大了时间消耗.文献[14]在GMM基础上提出一种基于熵惩罚极大似然估计的EM算法.该算法在不完备数据和缺失数据之间建立条件熵模型，通过不完备数据降低缺失数据的不确定性.实验表明，该算法能有效适应模糊梯度模型，提高分割精度.

上述部分算法中，虽然对偏移场进行了修正，通过不同的方式添加空间信息约束，在一定程度上提高了分割精准率，但在噪声下和细节上的处理仍然不够理想.针对上述问题提出基于MRF的分层高斯混合模型，在SCGMM算法[15]的基础上，受文献[16]的思想启发，将传统的高斯混合模型中的高斯分布进行分层处理，由下层的高斯混合模型的联合概率密度代替上层的高斯分布，并对图像像素点使用MRF进行建模，将获取的后验概率结合邻域信息作为上层的先验概率.该方法引入了邻域像素类别信息，并使用分层更新先验概率，有效提高了分割精度，并在一定程度上提高了抗噪性.

1 算法原理

受文献[15-16]的启发，本研究定义了一种分层高斯混合模型，并引入基于MRF的图像相邻像素信息，利用EM算法进行模型求解，实现脑部MR图像分割.

1.1 高斯混合模型和EM算法

使用高斯混合模型进行图像分割，就是利用高斯概率密度函数来进行建模.假设图像X含有N个像素点X=(x1，…,xn)，且由K个类别构成.使用GMM进行建模，定义第i个像素点服从K类高斯混合分布，像素点xi的密度函数定义为：

(1)

(2)

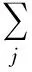
(3)

GMM可以利用EM算法(最大似然估计法)进行参数估计，依据最大后验概率准则来实现图像分割.基于上述图像，假设像素点之间相互独立，定义GMM联合条件概率密度即似然函数为：

(4)

在计算联合概率密度时，为了避免下溢，对式(4)取对数进行优化，从而得到对数似然函数如下：

(5)

1.2 基于MRF的分层高斯混合模型

使用传统的GMM进行图像分割建模时，图像由K个高斯分布组成.本算法在传统GMM的基础上增加分层处理，将K个高斯分布再次进行K次高斯混合建模，即使用高斯混合模型替代第kj个高斯分布.假设图像X含有N个像素点，X=(x1，…,xn)，定义如下密度函数将图像划分为K个类别.

(6)

其中:G(xi|Θjr)为高斯分布，参数集={πij，j=1，2…K，i=1，2…N}，参数集Θ={μjr，∑jr，j=1，2…K，r=1，2…R}.πij表示像素点xi隶属第j个类别的先验概率，ηjr表示此像素点隶属第j个类别中第r个高斯分布的先验概率.具体的分层框架如图1所示.

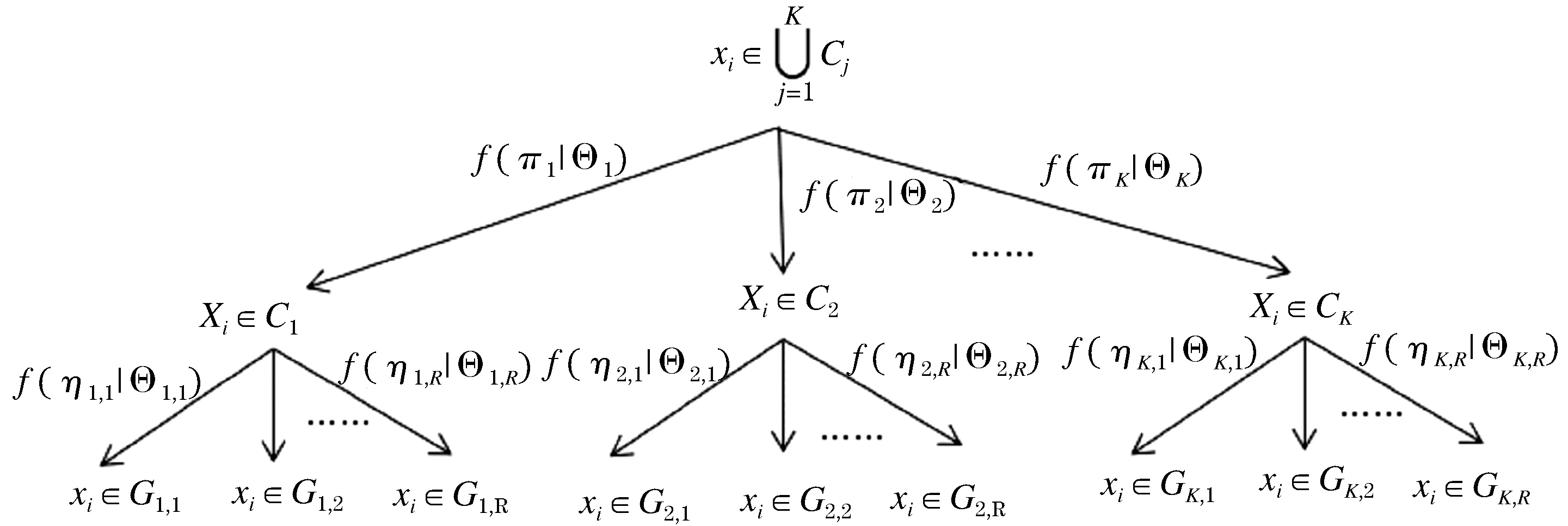
图1 分层高斯混合模型Figure 1 Hierarchical Gaussian mixture model

为了增加抗噪性，在分层高斯混合模型中引入MRF，通过贝叶斯定理(7)可知联合概率密度函数(8).

p(Π,Θ|Y)∝p(Y|Π,Θ)p(Π)

(7)

(8)

(9)

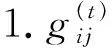
(10)

(11)

(12)

(13)

取对数似然函数式(14)

(14)

对式(14)进行迭代估算，当log(t+1)-log(t)<0.1停止迭代，最大化后验概率函数Zij，进而实现图像分割.

1.3 算法流程

1)初始化待分割图像类别数K、分层高斯分布数R、迭代次数t、邻域大小以及平滑参数β.随机初始化式(6)的先验概率πij、ηjr、μjr和∑jr；

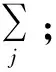
3)E步：根据式(10)计算后验概率Zij，t=t+1；

5)计算式(14)的值，若log(t+1)-logt<0.1，则停止迭代，否则，继续执行步骤3)；

6)停止迭代后，取最大后验概率，完成图像分割.

2 实验结果与分析

2.1 实验数据

实验样本分两类，一类是来自BrainWeb网站提供的仿真脑MR图，包含不同噪声条件下的T1加权图像，另一类是nitrc网站提供的真实临床脑MR图.本文实验方法基于MRF的分层高斯混合模型MLGMM与传统GMM、基于Dirichlet分布的Dgm[17]和基于邻域约束的SCGMM[15]三种方法进行比较.

2.2 评估指标

对于图像分割的评估一般是通过比较待评估的分割与标准分割之间的距离或者相似度来实现.本文选取文献[18-19]中基于区域重叠的DICE和误分率MCR作为评估指标，DICE越大表示分割效果越好，而MCR越小表示分割精度越高.

(15)

其中：Sseg和Sgt分别代表待评估分割区域和标准分割区域，DICE指标也可由TP、FP、FN和TN四个公共基数组成.根据式(16)表示，TP=m11，FP=m10，FN=m01，TN=m00.由此可知，TP表示A类被正确划分的像素点个数，FP表示B类被误分为A类的像素点个数，FN表示A类被误分为B类的像素点个数，TN表示B类被正确划分的像素点个数.

(16)

(17)

2.3 仿真脑MR图

本节分别采用BrainWeb网站提供的两组不同噪声条件下的T1加权仿真图像作为实验样本，并以网站提供的标准分割作为对比.在本实验中，K取3，R取4，β取2，图像邻域取3×3.

图2、3为1%和3%的噪声条件下，本研究方法与其他三种方法分割数据集中第40张、第48张、第60张和第91张图片的对比结果.表1～8分别是1%和3%噪声条件下这四张图片的分割精度对比.图2、3中的(A)为实验原图，(B)为标准分割结果，(C)～(F)分别为GMM、Dgm、SCGMM和MLGMM的分割结果.

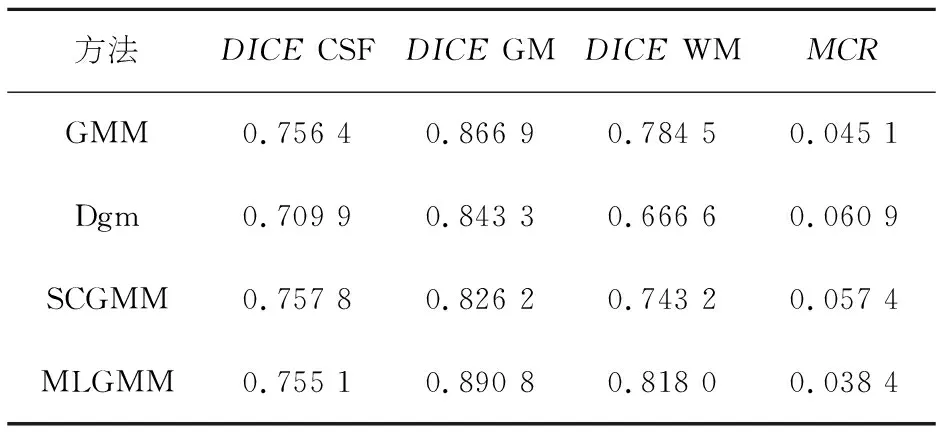
表1 第40张仿真图像1%噪声下分割精度对比

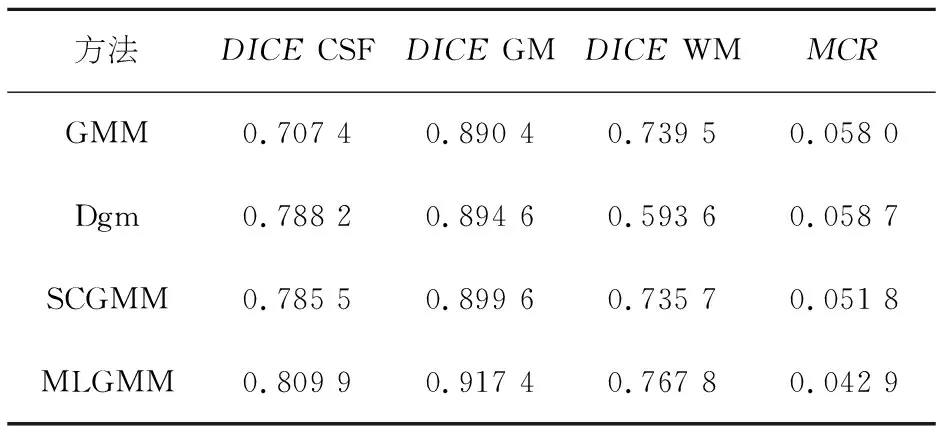
表2 第48张仿真图像1%噪声下分割精度对比Table 2 Comparison of segmentation accuracy of the 48 th simulation image with 1% noise

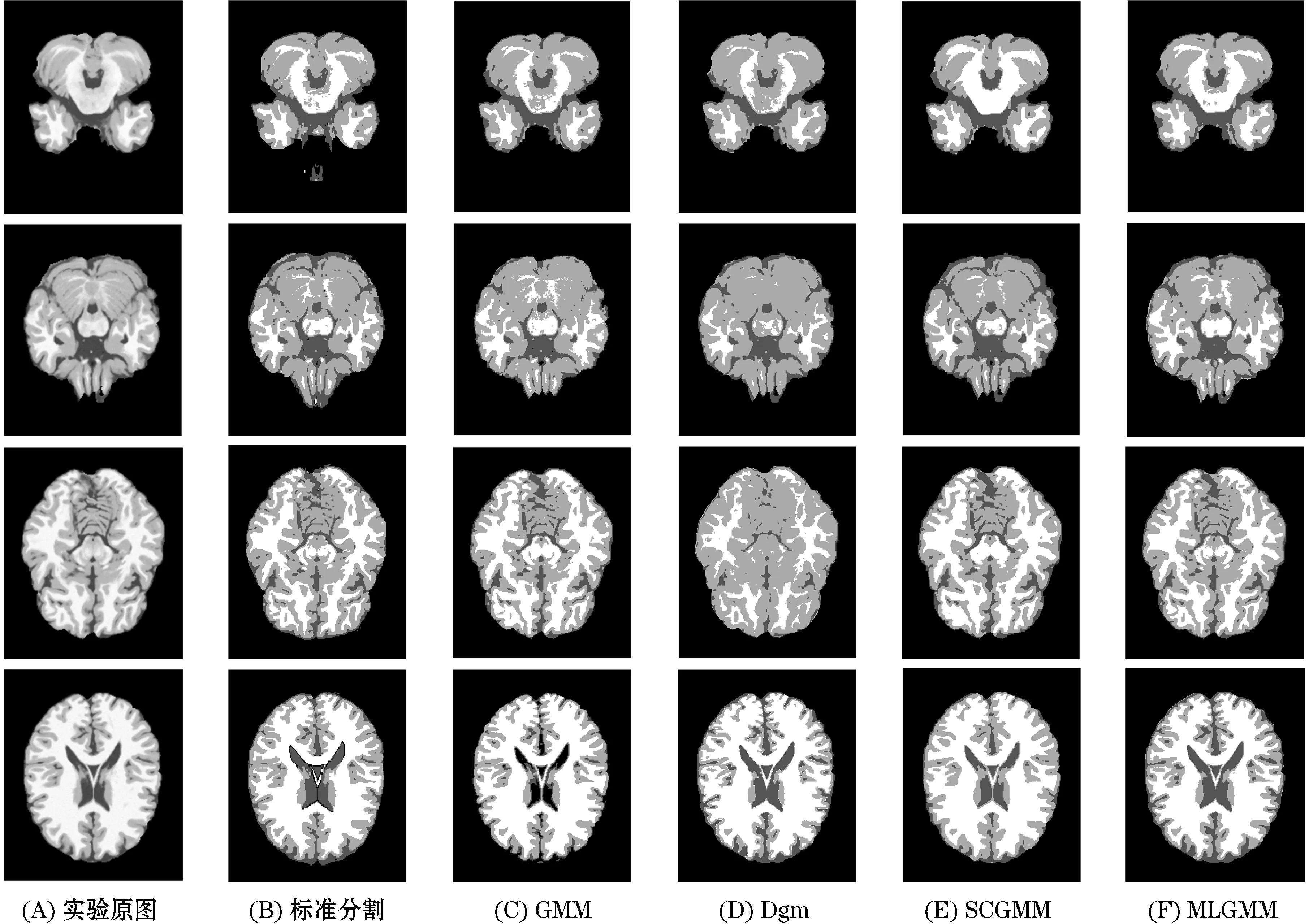
图2 四张仿真脑MR图1%噪声下分割效果Fiure 2 Segmentation results of four simulated brain MR images with 1% noise

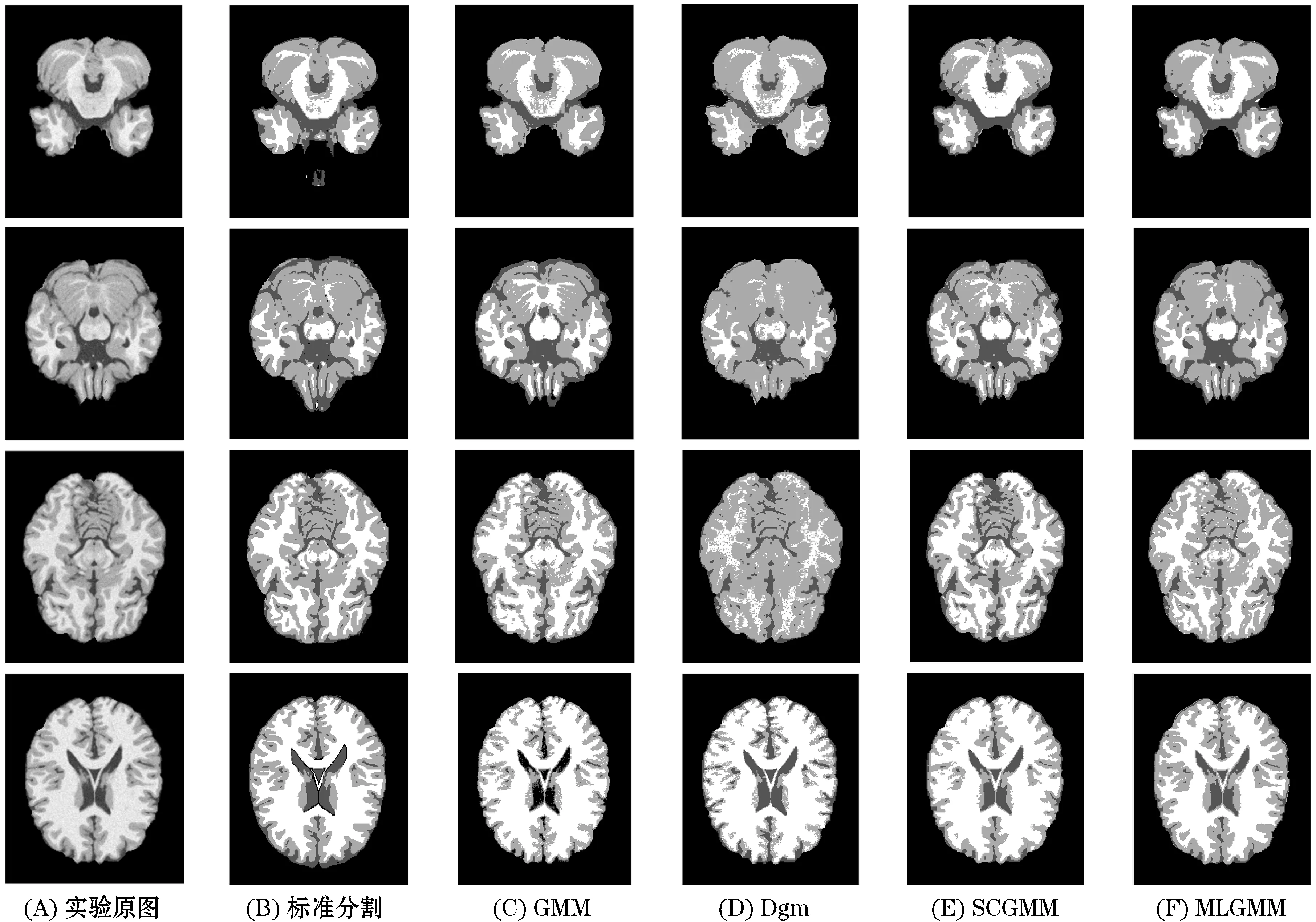
图3 四张仿真脑MR图3%噪声下分割效果Figure 3 Segmentation results of four simulated brain MR images with 3% noise

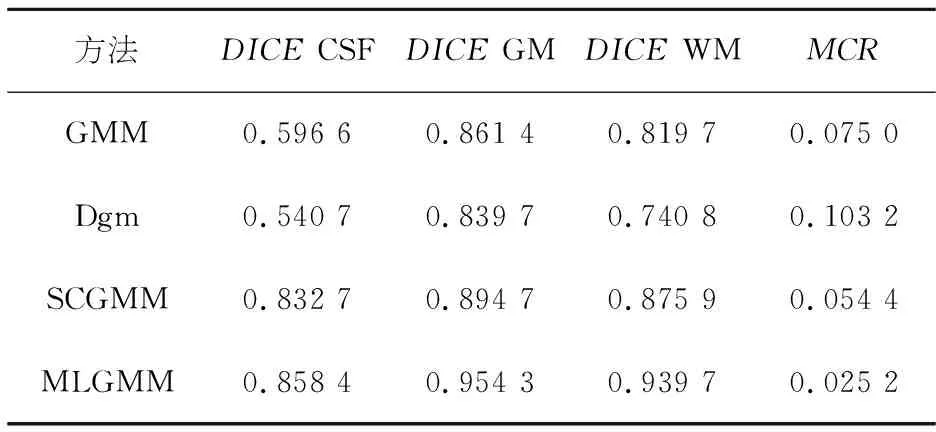
表3 第60张仿真图像1%噪声下分割精度对比Table 3 Comparison of segmentation accuracy of the 60 th simulation image with 1% noise

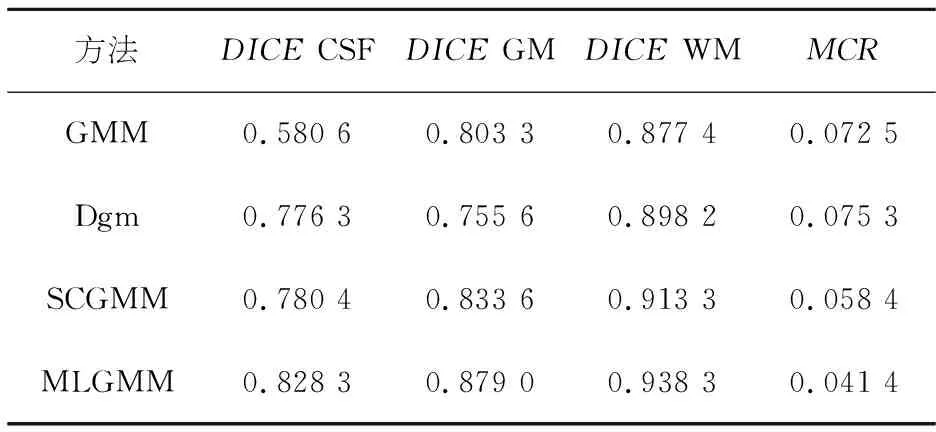
表4 第91张仿真图像1%噪声下分割精度对比Table 4 Comparison of segmentation accuracy of the 91 st simulation image with 1% noise

由表2～4可知本文方法在CSF、GM和WM的分割上均优于其他三种方法，表1中GMM、SCGMM和本文方法在CSF上的分割较为接近，但在GM和WM的分割上，本文方法明显优于GMM、Dgm和SCGMM.同时本文方法在MCR上的表现也优于其他三种方法.由图2可知，本文方法与其他实验方法相比，对于细节处理更佳.

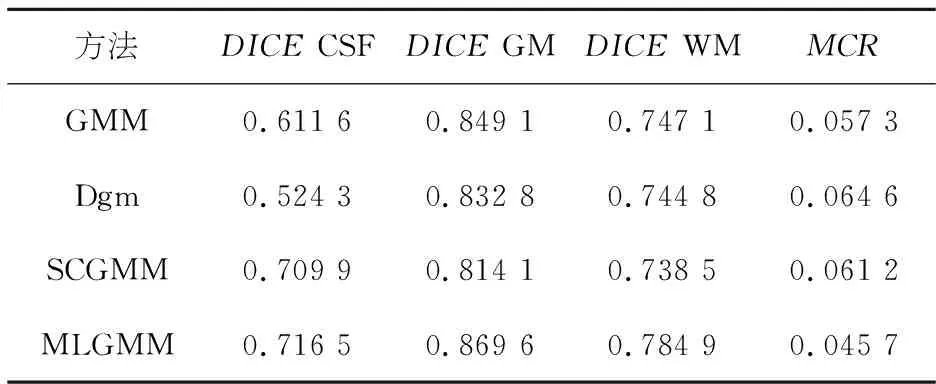
表5 第40张仿真图像3%噪声下分割精度对比Table 5 Comparison of segmentation accuracy of the 40 th simulation image with 3% noise

由表5～8和图3可知，GMM、Dgm和SCGMM在噪声影响下对脑组织的分割都受到不同程度的影响.GMM和Dgm对CSF的分割表现较为不稳定，SCGMM虽然未表现出较大波动，但在噪声影响下，MCR也有了一定程度的提高，且对GM和WM的分割结果也受到了影响.而本文方法由于采用了分层构建，并考虑了邻域信息，所以表现较为稳定，在对CSF、GM和WM的分割中，各项指标数值没有大的浮动，说明本文方法对噪声有一定的鲁棒性，且分割三种脑组织的DICE指标和MCR也优于其他三种方法.

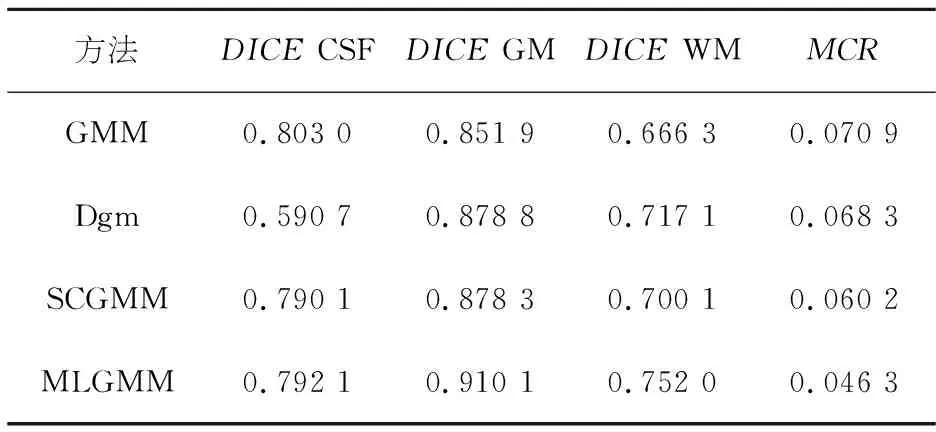
表6 第48张仿真图像3%噪声下分割精度对比Table 6 Comparison of segmentation accuracy of the 48 th simulation image with 3% noise

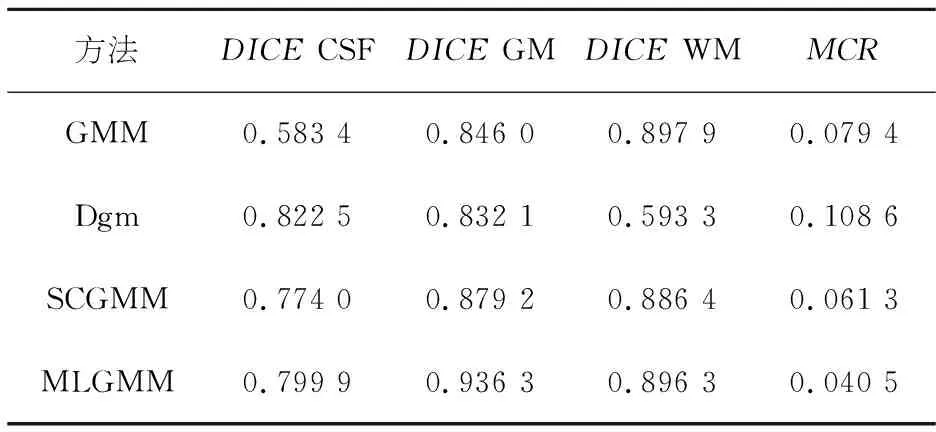
表7 第60张仿真图像3%噪声下分割精度对比Table 7 Comparison of segmentation accuracy of the 60 th simulation image with 3% noise

表8 第91张仿真图像3%噪声下分割精度对比Table 8 Comparison of segmentation accuracy of the 91 st simulation image with 3% noise

2.4 临床脑MR图

本节分别采用nitrc网站提供的临床脑MR图作为实验样本，并以网站提供的标准分割作为对比.在本实验中，K取3，R取4，β取1，图像邻域取3×3.

图4为本研究方法与其他三种方法分割IBSR05数据集中的第38张、第46张、第53张和第71张临床脑MR图的对比结果.表9～12是这四张临床脑MR图的分割精度对比.

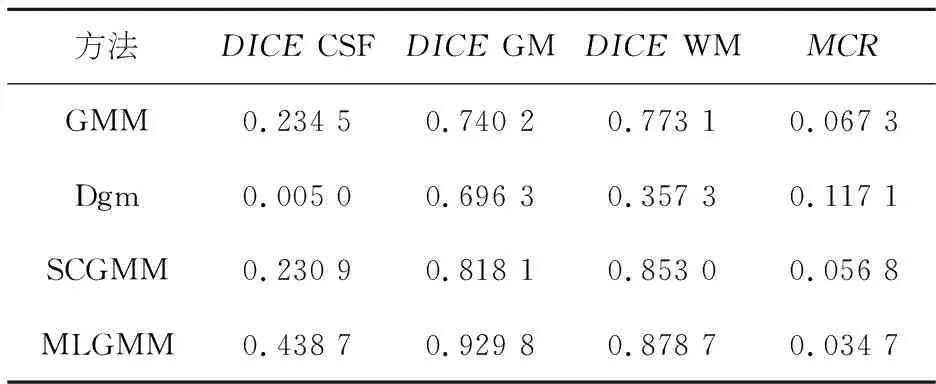
表9 第38张临床脑MR图分割精度对比Table 9 Comparison of segmentation accuracy of the 38 th clinical brain MR image

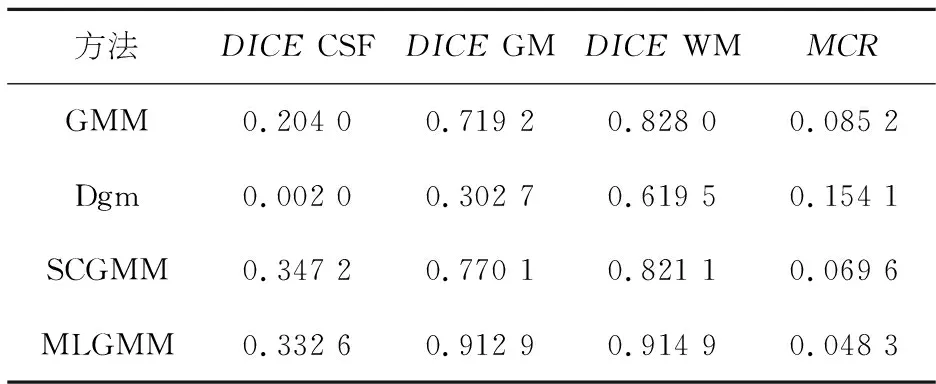
表10 第46张临床脑MR图分割精度对比Table 10 Comparison of segmentation accuracy of the 46 th clinical brain MR image

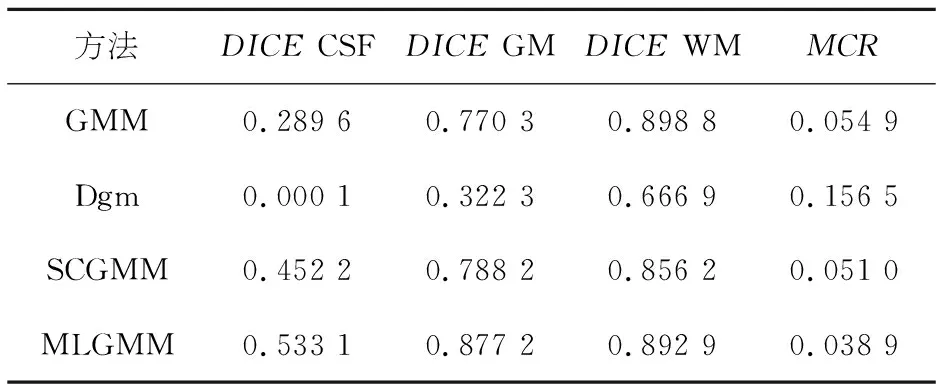
表11 第53张临床脑MR图分割精度对比Table 11 Comparison of segmentation accuracy of the 53 rd clinical brain MR image

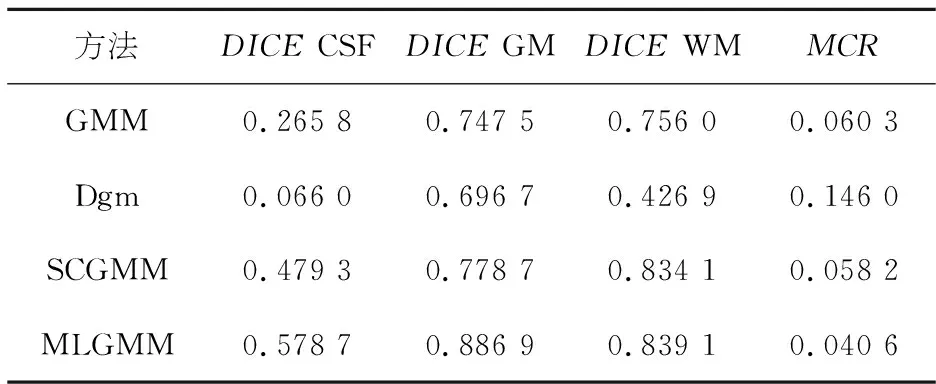
表12 第71张临床脑MR图分割精度对比Table 12 Comparison of segmentation accuracy of the 71 st clinical brain MR image

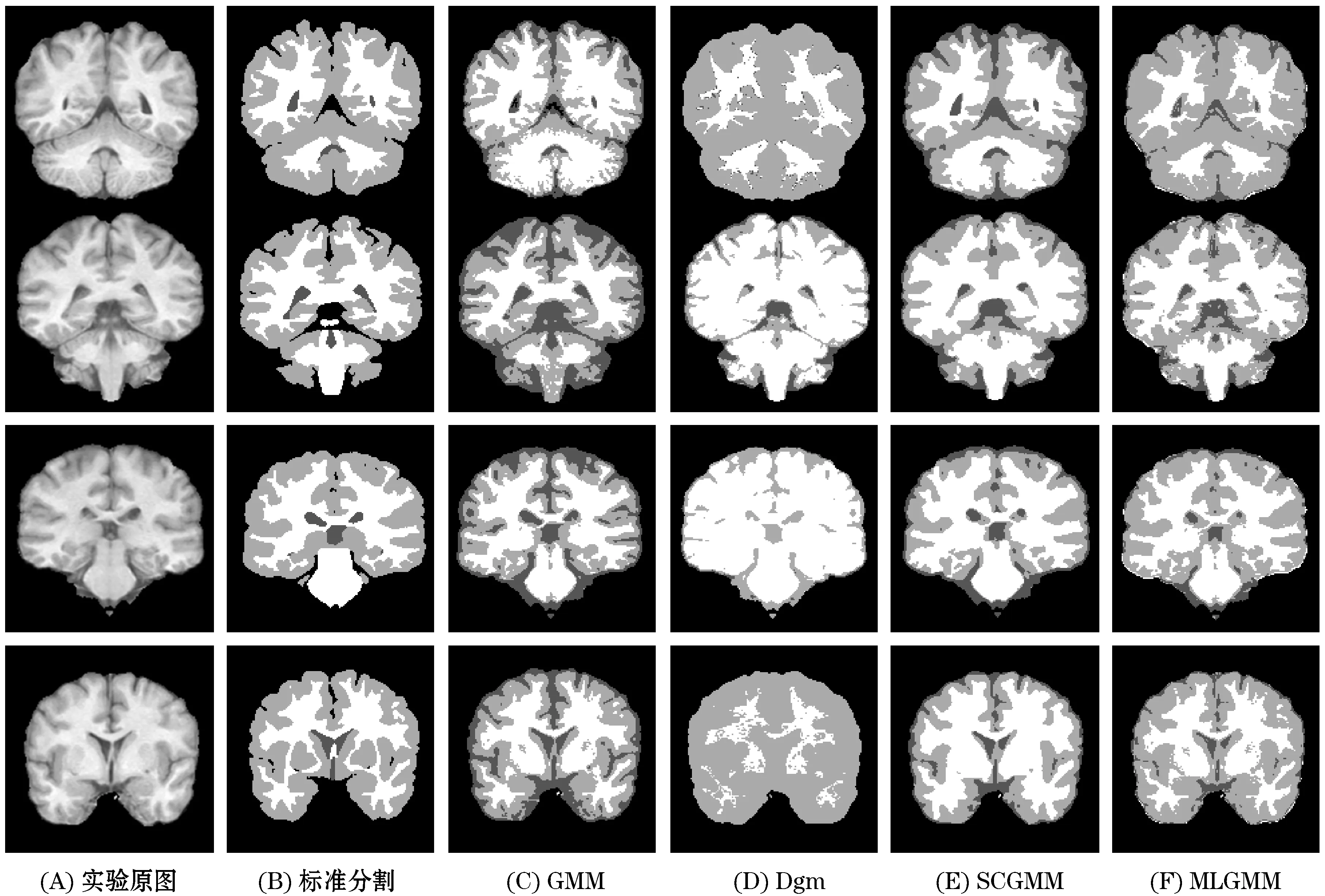
图4 四张临床脑MR图分割效果Figure 4 Segmentation results of four clinical brain MR images

表13是IBSR05数据集中10张临床脑MR图MCR的对比结果.由表9～12和图4可知在四种分割方法中，Dgm的分割结果最差，不仅MCR高，且对CSF、GM、WM的分割结果也非常不理想.GMM对GM和WM的分割情况尚可，但对CSF的分割情况表现不佳.而SCGMM由于引入了邻域信息约束使得该方法对CSF的分割精准率与GMM和Dgm相比有了很大的提升，但在细节处理上仍不够完善.本文方法在MCR上与其他三种方法相比有了明显降低，且对CSF、GM和WM的分割精度上也优于SCGMM，分割结果在细节上处理的更好，与标准分割最接近.

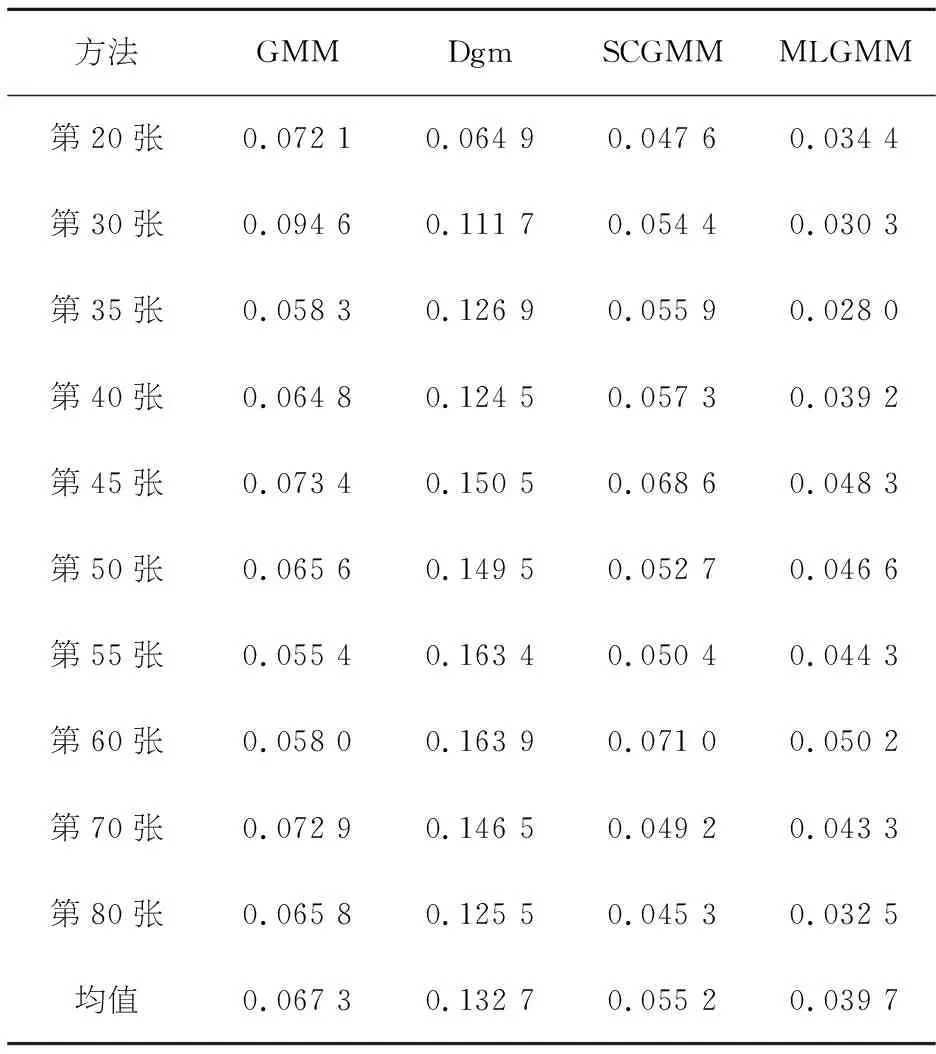
表13 10张临床脑MR图分割MCR对比Table 13 Comparison of segmentation MCR of 10 clinical brain MR images

3 结 语

本文提出一种新的分层高斯混合模型融合MRF的分割算法.该模型在GMM的基础上引入分层概念，将高斯混合模型中的高斯分布替代为高斯混合分布，并引入MRF对像素点进行建模，结合后验概率更新传统的GMM中的先验概率，有效解决了GMM用于图像分割时噪声敏感问题.实验表明，本研究方法与GMM、Dgm和SCGMM方法相比，在两类实验样本上都取得了较高的分割精度和更低的误分率，分割结果最接近标准分割.但本研究方法的不足之处在于初始模型GMM对噪声的鲁棒性表现不佳，因此置换初始模型提高模型对于噪声和偏移场的鲁棒性将是后续的研究方向.