教一条思路，学一种思维

李宇韬 刘东伟

一、关注学生的困惑，给出贴切表象

师：（回忆解决问题的步骤后）你在解决问题时，觉得哪个步骤比较难？

生：分析与解答。

师：跟他有同样想法的举手。老师跟你们的想法一样。今天，我们不仅要解决一道题，还要一起发现解决问题的法宝。这个法宝和导航有关。用过导航吗？导航有什么好处？

生1：假如我们想去一个地方不知道怎么走，我们就可以看导航。

生2：我们忘记了新家，可以用导航回去。

师：是的，导航可以给我们提供正确的路线。如果我们分析问题时也有这样的导航，告诉我们先想什么、再想什么，问题是不是很好解决了？（板书：思考导航图）其实这幅思考导航图一早就藏在大家的大脑里了，可能你平时没怎么在意，今天我们一起来发现藏在我们分析与解答问题背后的思考导航图。

评析：李老师通过谈话找到了学生的困惑点，使学生回顾三步骤的同时，又对三步骤有更多的感性认识。在学生提出困惑时予以共情，并为了解决困惑给学生提供了“导航”的表象，用“思路”形如“导航”这样的概念拉近了知识与生活的距离，增强了学生学习的信心。

二、画图表达题意，明确条件和信息

师：（出示例题：妈妈买3个碗用了18元。如果买8个同样的碗需要多少钱？）读完题目，你知道了什么？

生：妈妈买了3个碗，用了18元。

师：还知道了什么？你来帮她补充。

生：如果买8个碗，多少钱。

师：很好，你看你们用自己的话把题目把相关的信息说出来了，但是你们理解了吗？你能画图表示题目中的数学信息和问题吗？

（展示环节）

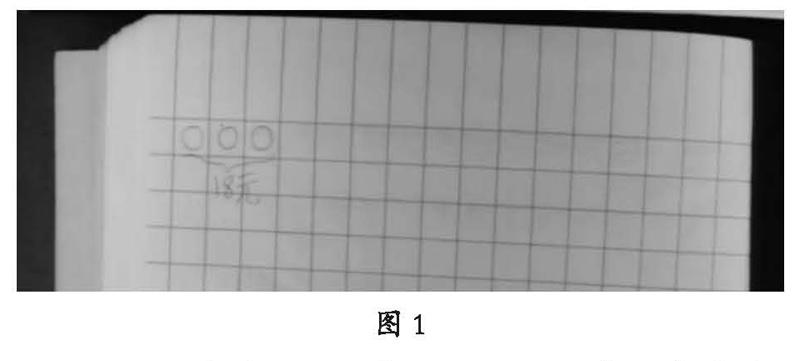
图1

师：（展示图1）这幅图数学信息完整吗？问题清楚吗？

生：还有8个碗要画出来。

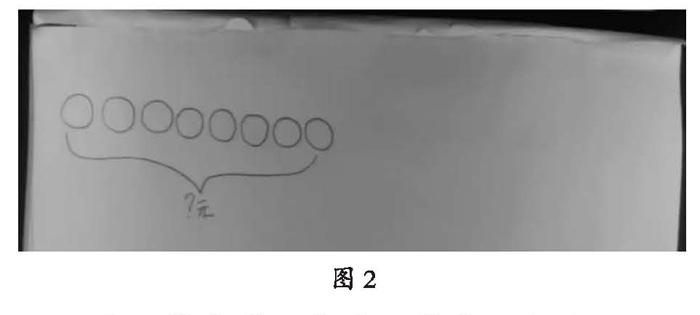
师：你觉得缺少一些信息要画出来是吧？那这幅呢？（展示图2）

图2

生：要先画三个碗，再画8个碗。

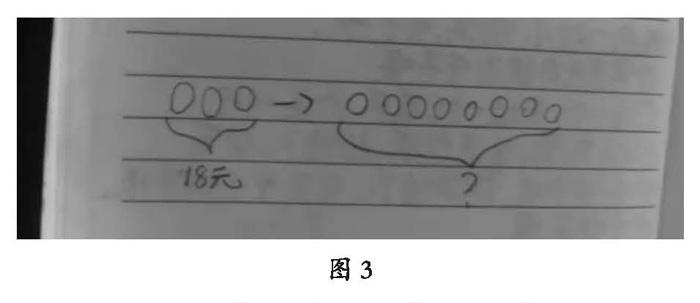
師：那你的意思是把这位同学的图，和刚才的怎么样？（生：结合起来）就可以了是吗？是这样吗？（展示图3）

图3

师：所以我们在画图表示题意的时候，不但要把信息，也要把问题都表达完整。老师也是像刚才这些同学一样表达的。

评析：学生在处理信息的时候，把“买8个同样的碗”不看做条件，而是归为问题。所以在展示学生画作的时候，李老师也选取了两种“漏条件”的作品与之呼应，使学生发现自己思路中的问题——没有时时紧扣条件或问题。通过作品对比再一次强调完整表达的重要性。学生在这个过程中辨析了“条件”与“问题”，并了解到两者结合才能组成完整的数学问题。

三、尝试使用分析法，理清思考过程

师：第一步，我们完成阅读与理解了。第二步，难点来了——分析与解答。接下来我们要从哪里入手呢，该怎么想才能找到我们的算式呢？

生：看已知信息，18÷3。

师：嗯，这是一、二年级时我们常用的方法，题目中给出的条件正好能解决相应的问题。三年级开始，问题开始变得复杂了，是不是一定能按所给条件列算式？你看。（出示：妈妈买3个碗用了18元，买5个杯子用了20元。如果买8个同样的杯子，需要多少钱？）

师：这道题也是先算18÷3吗？为什么？

生：不是。有些是多余信息，给了我们障碍信息。

师：那就是说，看到信息就列算式有可能会（生：错）那从哪里入手去想，才能准确找到有用的信息？

生：从问题入手。

师：（出示：要解决的问题）我们今天要解决的问题是？

生：需要多少钱？

师：（出示：需要多少钱）你生活中买东西付钱，想知道需要多少钱，得先知道什么？（出示：需要的条件）

生：知道那个东西多少钱。

师：是一个东西，还是全部东西。

生：一个东西。

师：还有吗？

生：买了几个。

师：同学们的生活经验很丰富。那我们去买碗付钱，就要知道（出示：买几个碗，一个碗多少钱）售货员才能算出你要付多少钱。这两个条件都是我们需要知道的，但哪个是已经知道的了？（出示：已知的条件）

生：知道买8个碗。（出示：买8个）

师：那就是剩下“一个碗多少钱”我们需要知道，但是却还不知道，它就变成了我们的一个（生：问题）。非常棒。这个新问题跟刚才“需要多少钱”比起来，是先解决还是后解决？

生：先解决。

图4

评析：李老师尝试引导学生使用分析法解决问题，明确分析过程中的三个要素：要解决的问题，需要的条件和已知的条件。而且李老师还把分析法和综合法进行了简单的对比，使学生体会综合、分析各自的价值：综合法在已知信息恰好对应问题时显得高效，但是当众多的已知信息中存在干扰信息，那分析法更能帮助我们避免干扰，高效解决问题。

四、绘制思考导航图，巩固思路认知

师：回顾一下我们的思路是怎么来的。我们首先从哪里入手？

生：从问题入手。（出示：要解决的问题）

师：为了解决问题，接下来要找到什么？

生：需要的条件。（出示：需要的条件）

师：再看看这些条件，有的条件是已知的，有的是（生：未知的）。那未知的条件，它会变成我们的一个新的（生：问题）。先解决了它，我们就能把未知的变成（生：已知的）。那这样的思路走下去，我们就能完整地解决整个问题了。

图5

评析：通过回顾分析与解答的全过程，李老师为学生绘制了一幅“思考导航图”，这幅图直指分析法。分析法为学生提供了思考的方向，遵循这样的程序循环往复可以解决问题。但没有建立这样的表象时，其思维价值不能得到充分发挥。思考导航图的外观就像一幅简化的“流程图”，它使学生的思路变得可视，让学生找到推理的起点、过程和终点，在后续的学习中也不至于胡乱下手或手足无措。但更重要的是，学生也因此加深、巩固了对思维的认知。

也就是说，一幅并不尽善尽美的“导航图”“流程图”“思维导图”……能从视觉上刺激学生发生深度学习。我们暂时不能判断“看见思路”比“听见思路”来得更有效，但李老师的的尝试具有开拓性的意义。李老师给无形的思维一个恰当的表象，学生得到的不仅仅是针对本类题型的思路，还学到了“分析法”这种逻辑推理的思维形式——他们看见了一条思路，也学到了一种思维。此后再出现其他思维形式的时候，我们才可以期待学生成为“思维画家”，愿意尝试用图表符号表达自己脑海中的思考，更容易触及未知的远方。

[本文系广东省教育科研“十三五”规划2020年度重点项目“小学数学精准教学理论的构建与实践”（课题批准号：2020ZQJK027）的阶段性成果]