基于遗传光学算法的镜片加工车间布局优化*
2021-03-01马玉莹张家骅
马玉莹,张家骅
(无锡工艺职业技术学院机电与信息工程学院,江苏 宜兴 214206)
0 引言
车间设备布局优化是指在满足约束的条件下,在已知的工作区域对设备进行布局来实现某些生产目标。设备布局对于企业提高生产效率,降低生产成本有着重要意义[1]。由于车间设备布局问题被证明是NP-hard问题,采用确定性优化方法求解效果不理想,智能优化算法是解决此类问题的主要方法[2]。遗传算法、粒子群算法、蚁群算法等已经被成功用来解决设备布局问题[3-5],其中遗传算法是主流算法[6]。肖国红等采用遗传算法求解了以最小化物料搬运费用为目标的镜片加工车间布局优化问题[7]。但是实际生产中往往存在多个优化目标;而且传统遗传算法存在容易陷入局部最优等缺点[8]。通过不同算法的混合,能够提高单一算法的搜索性能;光学优化算法是一种新的群体智能算法,并在连续问题上被证明优于粒子群算法[9]。因此本文根据企业实际情况,以最小化镜片车间设备间物流搬运费用和设备包络面积为优化目标建立多目标模型,并开发了一种遗传光学算法,来求解设备布局方案。
1 问题描述及数学模型
在矩形布局的车间内,确定形状和尺寸已知的磨削机等设备位置;出于物料要求,设备分行排列,设备间存在间距要求。图1是车间设备布置示意图。

图1 车间设备布置示意图
该问题的目标函数如下:
minF=ω1f1+ω2f2
(1)
(2)
f2=Sl/β
(3)
Dij=|xi-xj|+|yi-yj|
(4)
xi=xk+(li+lk)/2+hik+Δi=
hk0+Δk+(li+2lk)/2+hik+Δi
(5)
yi=(t-1)d+d0
(6)
Sl=H×[(m-1)d+d0+
0.5max(wi)-(d0-0.5max(wj)]
(7)
式(1)是目标函数,同时最优化目标f1和f2,采用加权法将双目标优化问题转换为单目标,ω1和ω2是加权系数,由企业专家给出,ω1+ω2=1;式(2)和式(3)分别是目标函数物料搬运成本和布局结果所包络面积,式中Pij为设备i和j之间的搬运费用,Qij为设备i和j间物料搬运频率,m为车间总行数,n为设备数量,Sl为车间布局包络总面积,式中α和β由预先调试给出,对目标函数进行归一化处理;式(4)中Dij为设备i和j之间距离;式(5)为第i台设备横坐标,li为设备长度,hij为设备i和j间的横向最小间距,hi0为设备i和车间边界间的横向最小间距,Δi为设备i和i-1或边界间净间距;式(6)为第k行的第i台设备的纵坐标,d为设备行间距,d0为第一行设备到车间边界的距离; 式(7)中H为车间宽度中wi为最后一行上的设备的宽度,wj为第一行上的设备的宽度。
该问题的需要满足的约束是:
xi,yi≥0,Δi>0,
(8)
|xi-xj|≥[(li+lj)/2+hij]λikλjk
(9)
λik={0,1}
(10)
(11)
i,j,k=1,…,n;t=1,…,m
式(8)是设备坐标和设备间净间距非负要求,式(9)要求同一行设备不能重叠。式(10)表示当设备i布置在第k行,决策变量λik=1,否则为0;式(11)要求一台设备只能出现一次。
2 遗传光学算法
本文通过将光学算法混合到遗传算法中,设计一种遗传光学算法来求解镜片加工设备布局问题。
2.1 光学算法
光学优化算法是Kashan在2015年设计的一种新型群体算法,并已在连续问题上证明该算法要优于粒子群等算法[9]。该算法将被优化函数曲面的局部凹凸性质比拟成凹、凸镜,将可行解比作光源,光源经凹、凸镜成像后的点为更新后的解。因为光源的位置不同,从而呈现大小不同的像,实现算法的探索与利用。该算法的原理如图2所示,焦距f,球面半径r(r=2f),物距p,像距q,球面镜物像公式:
2/r=1/p+1/q⟹q=rp/(2p-r)
(12)
球面镜放大率公式:
m=-q/p=HI/HO⟹HI=-HO·q/p
(13)
在光学优化算法中,将问题的初始解表示为一系列初始光源的位置,光线在已知光学参数的镜面上不断反射成像,即通过式(12)、式(13),可将光源点位置p和HO,换算得到像点的位置q和HI,从而实现解的更新。
王金叶等[10]对光学优化问题进行了进一步研究,提高了算法性能。但目前主要光学优化算法研究的是连续性问题,还没有研究设备布局这类离散问题。

图2 光学优化算法原理图
2.2 遗传光学算法流程
遗传算法是通过模拟生物进化过程实现优化目标,包括选择、交叉、变异操作;其中变异算子存在盲目变异的缺陷,使算法易陷入局部最优。本文将光学算法取代遗传算法的变异算子,来提高算法的寻优能力。图3是整个遗传光学算法的流程图。

图3 遗传光学算法流程图
2.3 染色体的编码和解码
由于光学算法解的更新函数是连续型,要使该算法适合离散问题,编码和解码很重要。本文采用连续性编码,染色体长度2n,基因值取值范围[0,Δ],其中Δ为设备之间的最大净间距。例如有3台设备,设备之间的净间距[0,2],可如图4进行编码,保证了染色体可以使用连续函数的更新方法。
采用面向设备的原理进行解码,如图4编码段进行解码的时候,基于部分优先权解码策略,对前半段的染色体按照基于优先权位置排列,后面的基因值不变。这样设备布置顺序是1-3-2,这个顺序下的设备间的净间距是1.4、1.1、1.7。
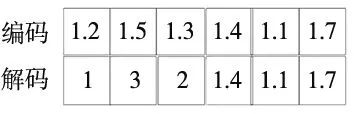
图4 染色体编码与解码
2.4 选择算子和交叉算子
在求解最小化问题时,采用竞标赛选择,可以避免采用轮盘赌算子时需要适应度值转换问题,并获得更好性能[11]。因此,采用竞标赛选择,随机选中两个个体,适应度值好的个体,进入到进化过程中。交叉算子采用均匀交叉,因为这种方式能够产生较好的个体后代,破坏能力较小[12]。
2.5 光学优化

(14)
最后,将光学优化后的种群与原种群进行比较,将目标函数值好的染色体保留形成新的种群,进行下一次进化,直到满足迭代要求。
3 实例研究
光学镜片加工车间120 m2(12 m×10 m),需布置10台设备(4台磨削机,4台抛光机,2台清洗机),具体尺寸如表1所示,表2是设备间的物料搬运费用Pij,表3是设备间物料搬运频率Qij,设备间横向最小距离hij=2 m,设备与车间边界的最小间距hi0=1.5 m,两设备间的净间距Δ的取值范围为[0,1.5]m。第一行设备与车间上边界之间的距离d0为1.5 m,车间行间距d为2 m。

表1 待布局设备尺寸 (m)
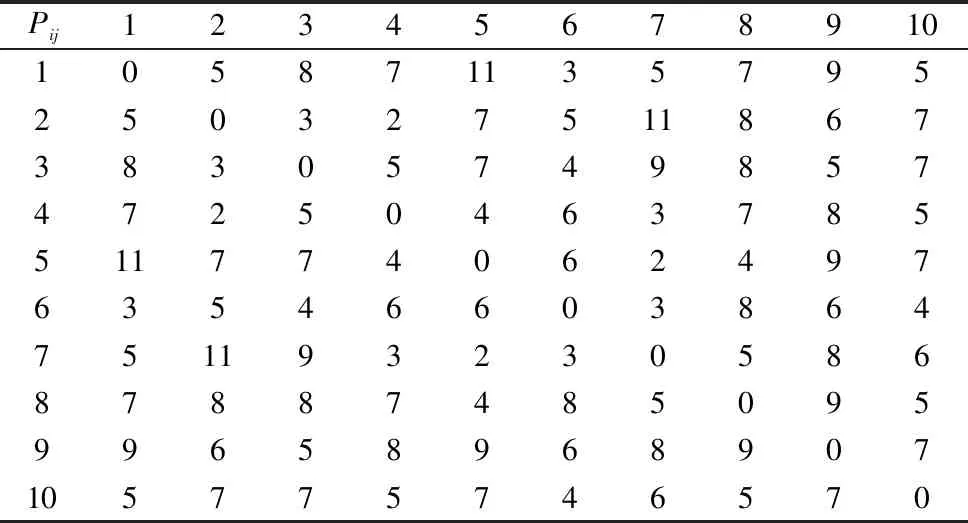
表2 单位物料搬运费用Pij
分别采用文献中的遗传算法(GA)[3],自适应遗传算法(AGA)[13]与本文遗传光学算法(GOA)的结果进行对比。优化过程中算法的参数如下:ω1=0.5,ω2=0.5;由企业现场工程师给定;目标函数标准化系数α=6742,β=68;种群数量100;最大遗传代数为600;GA中交叉率pc=0.8;变异率pm=0.2;AGA中自适应参数与文献[13]设置一致;GOA中,光学更新系数Pc=0.7。由于GA和AGA中用的是轮盘赌算子,因此目标是最大化适应度值,为了对比,对适应度值进行了转化,结果给出了最小化目标值。

表3 设备间物料搬运频率Qij
图5是每个算法执行5次后的最优的目标函数值的收敛曲线。可以看到三种算法中,GOA的效果最好,GA的效果最差。这是由于普通GA容易陷入局部最优,而变异算子变异盲目。AGA算法虽然比GA算法得到了好的效果,但是从整个过程上看,AGA算法只是在算法后半段才开始发挥最用,在算法前半段,由于种群差异大,自适应参数并不发挥很大作用。从GOA算法的进化过程中可以看到,GOA算法整体趋势就表明该算法可以跳出局部最优解,往全局最优解的方向发展。
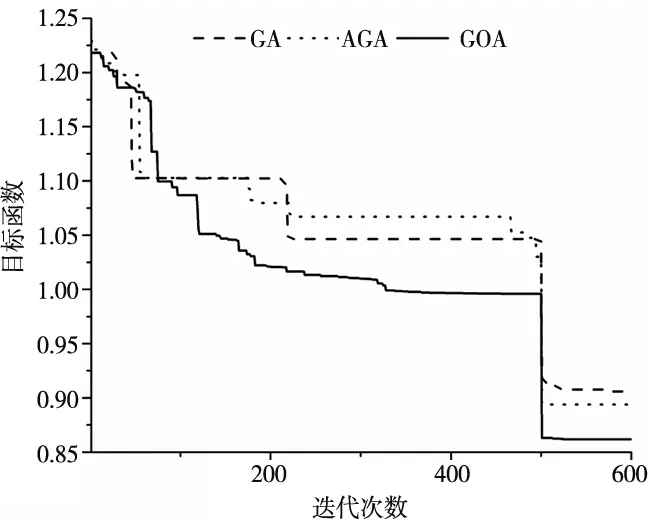
图5 不同算法适应度值收敛曲线
表4是最终获得的搬运费用值和设备包络面积,三种算法都可以得到相同的包络面积,但是GOA在搬运费用上,比GA的结果可以节约10%的费用。

表4 搬运费用和设备包络面积
4 结论
(1)根据镜片车间设备布局问题,建立了具有搬运成本和设备包络面积指标的多目标设备布局模型。
(2)针对传统遗传算法,采用竞标赛选择算子替换轮盘赌选择算子,光学优化算法取代变异算子,构造了一种遗传光学算法。
(3)实际案例计算结果表明,遗传光学算法通过将光学优化引入到种群进化环节,引导种群趋向最优方向收敛,避免传统遗传算法陷入局部最优,能得到比遗传算法质量更好的方案。
