基于改进的粒子群优化神经网络粗糙度预测模型*

史柏迪，庄曙东，韩 祺

(1.河海大学机械工程学院，江苏 常州 213022；2.梅特勒-托利多国际贸易(常州)有限公司，江苏 常州 213022；3.南京航空航天大学江苏省精密仪器重点实验室，南京 21009)

0 引言

金属零件加工后表面粗糙度直接决定零部件的配合性质、耐磨性、疲劳强度、接触刚度、使用寿命及各类力学性能，为必须被约束的重要参数。当前机械加工日益趋向超高精密化[1]，传基于统计学原理的多元线性[2]、以及非线性[3]回归预测模型以及无法满足实际加工需求。

当前机器学习与深度学习的浪潮之下为表面粗糙度预测提供了新的方案。国内外已经有了诸多研究，在机器学习算法中支持向量机(SVM)[4]，决策树[5]、K近邻[6]等在预测以及分类任务中均有广泛使用。但近年来深度学习算法在图像识别、特征工程、数据分析等领域相对机器学习算法均有更好的精度表现。且随着近年来国内外学者的进一研究，目前其可读性、表达能力、优化等问题有了较大改善[7-9]。但经网络初始化、梯度消失等“黑盒”问题依旧存在，在工程运用中直接影响神经网络模型的预测精度。基于此问题本文提出一种在初始化以及算法优化器两方面进行改进的神经网络。

神经网络初始化目前一般最为简单的方法为对各层神经元节点填充服从均值为0方差为1的高斯分布随机数。其次便是使用群体智能算法对神经网络参数进行预先筛选。目前常见有PSO-BP[10]、GA-BP[11]，但其本质为建立多个随机正态分布神经网络在此基础上对其参数按照特定算法进行更新，最终筛选出最佳个体。本模型使用Xavier[12]初始化来提高初始群体，减少模型陷入局部最小无法优化的概率。其次算法优化器为另一决定预测精度的方面，目前大多神经网络工具箱使用随机梯度下降(SGD)更新模型参数，但近年来优化器有着较大的突破[13-14]。本模型使用Ada Mod[15]优化器，经测试相对SGD与Adam优化器可有效提高模型收敛速度及预测精度。

1 建模条件

1.1 特征的选取

机械加工过程中表面粗糙度(Ra)受到材料特性、切削参数、机床特性、刀具选择等诸多因素的影响。本模型所使用的样本材料为U71Mn高锰钢因力学性能良好,具有较好的抗冲击与耐磨性能[16]，为中国铁轨的主要原材料。但当切削参数配置不合理时容易导致材料表面马氏体粗大，力学性能急速下降。为提高数据样本精确度，综合考虑实际加工情况以及材料特性，选择加工条件为三菱公司的M-V5CN组合机床，刀具为4齿平底立铣刀，刀具直径20 mm如图1所示。选取主轴转速n(r/min)、每齿进给量f(mm/z)、铣削深度ap(mm)、铣削宽度ae(mm)为输入特征。

图1 4齿硬质平底铣刀

输出特征为Ra(μm)由光电轮廓仪任选加工后表面三处均匀表面取均值获得，最终获取100组数据样本,表1为部分样本数据。

表1 部分样本数据

1.2 数据集的处理

为使模型模型具有良好的泛化性避免过拟合现象，对数据集按照图2进行划分。

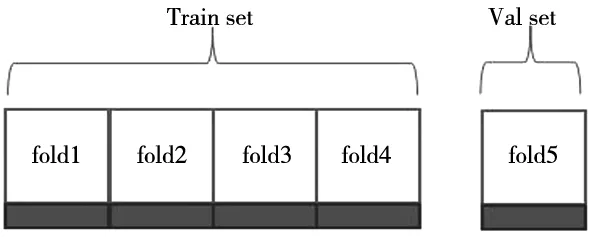
图2 5折交叉验证

此外从表1易知输入特征n较其他特征而言数值量较大为减少其对梯度传播的影响将4个输入特征按照公式(1)进行归一化处理:

(1)

式中，numnor为归一化后的数据，下标min与max为该输入特征的最小与最大值。i为该样本序号1≤i≤100。

2 神经网络初始化

2.1 高斯分布初始化

在隐藏层层数为n的BP网络中如果使用高斯分布初始化易得其前向传播通项公式(2):

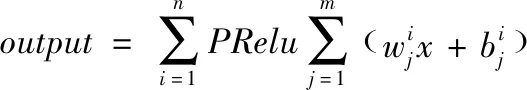
(2)

式中，n为隐藏层总数，i为当前隐藏层序号。m为在第i层情况下神经元的数目，j为在第i层的第j个神经元。w为i层第j个神经元的权值(w)，b为偏置(b)。PRelu为激活函数。

从式(2)中可知虽然其权值与阈值的分布均满足正态分布，可在一定程度里缓解激活值异常的情况，但是当网络隐藏层增加时激活值弥散情况依旧无法避免。经式(1)处理后所有输入值均分布在[0,1]取隐藏层数目依次为1、10、50，神经元数目固定为100，可得激活值变动如图3所示。

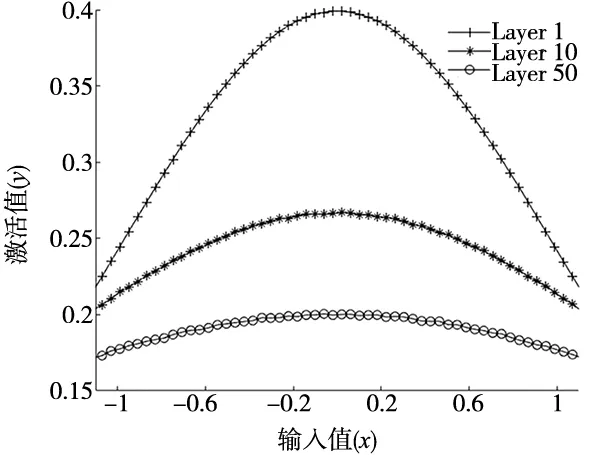
图3 高斯初始化输出激活值

由图3可知激活值伴随着层数的增加逐步平缓趋向0。根据统计学原理易知数据方差越大其包含的信息量越大。仅对各层神经网络权值与阈值基于随机高斯分布式(2)初始化，在模型后续训练会带来的梯度饱和现象，易对模型精度造成影响。

2.2 Xavier初始化

Xavier初始化创始者Glorot发现在一个m层的多层神经网络中初始化若仅使权值与阈值服从高斯分布，在输出时无法保留输入数据的方差特性。一个良好的网络初始化因使数据激活输出值服从高斯分布且保证输入时的方差特性保持不变即满足如下条件：

(3)

式中，Cost为代价函数因采用BP结构即为均方误差;h为隐藏层;z为实际激活输出值;i,j为任意两个神经网络的索引。

对于任何一个d层神经网络如果所有层规格一致且采用相同的初始化方法可得式(4)分布规律。

(4)

式中，W为权值的向量矩阵。

以上即为Glorot条件认为初始化不应仅从w与b着手，而应使各层的输出激活值和状态梯度的方差在传播过程中的方差保持一致。

结合式(2)～式(4)可知若各隐藏层神经元数目为k，为满足Glorot条件第i层权值矩阵，需满足式(5)分布规律。

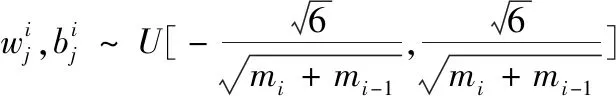
(5)

式中，m为隐藏层层数;i,j满足1≤i≤m；1≤j≤k;当神经网络采用式(5)初始化时可得值如图4所示。

图4 Xavier初始化输出激活值

由图4可知，随着神经层数量增加其各神经网络激活值的方差特性得到了最大程度的保留，有效解决了高斯初始化带来的梯度饱和问题。

3 基于Xavier的PSO算法

3.1 PSO初始化算法流程

PSO算法源于对鸟类捕食行为的模拟，每个粒子仅拥有速度与位置两个属性。在迭代中通过将个体极值与群体共享，所有粒子根据最优的个体极值决定下一轮的速度与位置。上述思想在BP神经网络中的运用可描述为在T次迭代之中，由n个粒子组成特征数量为D的大小为[n×D]种群矩阵X且其初始化符合神经网络规格为M的Xavier原则式(5)，粒子速度V为长度为D的向量。Pi为长度为n的向量对个体极值进行记录。Pg为群体极值。属性X与V按照式(6)进行迭代更新。

(6)

式中，ω为为惯性权重在后续进行讨论；d为当前维度1≤d≤D；i为当前粒子1≤i≤n;k为当前迭代次数1≤k≤T;c1,c2为加速因子取[0,1]常数；r1,r2为[0,1]的随机数通过添加扰动来阻止模型陷入局部最小值；为避免盲目搜索设置将速度约束在[-Vmax，Vmax];位置约束在[-Xmin,Xmax]。

在式(5)、式(6)的基础上可以给出该模型的PSO初始化模块算法流程如图5所示。

图5 基于Xavier的PSO初始化

图5即为算法流程，且在PSO中其超参数相对于基因遗传算法(GA)更易调节且,对于数据无需进行二进制编码重组具有极强的算法可移植性，以及较低的算法复杂度因此在PID控制、模糊逻辑控制以及神经网络初始化中有着广泛的运用。

3.2 惯性系数更新算法的选取

在PSO算法中惯性系数直接决定模型继承上一轮速度的能力，直接决定模型的收敛性以及全局搜索能力。传统常系数法虽可降低模型的算法时间复杂度但随着迭代的进行在经验区间[0,4,0.9]内选取任一常数在深层网络初始化中显然欠佳。Shi Y首先提出线性递减惯性系数法见式(7)。在此基础上还有如下常见策略式(8)～式(10)。

ω(k)=ωstart(ωstart-ωend)(T-k)/T

(7)

(8)

(9)

(10)

式(7)～式(10)中，各项参数在3.1节中均已说明。大量工程实践证明ω在开始时取0.9最终取0.4可使算法在中期有最佳的搜索能力在迭代终止前也可有效收敛。

设置粒子群数量(n)为100,最大迭代次数(T)为100。神经网络采取5层隐藏层可得神经网络结构图如图6所示。在图6结构之中计算可得神经网络有4×(100+1)+100×(100+1)×4+(100+1)项参数需要被初试化，即系数矩阵W为[101×405]。

图6 神经网络结构

本测试环境为pytorch使用cuda进行GPU并行运算。主机配置，CPU：i7 9750H,GPU：GTX1660TI，ROM：16G设置粒子群数量(n)为100,最大迭代次数(T)为100。按照式(7)～式(10)以及常系数0.6设置惯性系数ω得到表2。

表2 ω对模型影响

式(7)～式(10)实际耗时致均属于一个量级。固定系数法最终模型误差较线性递减法差距较大故不采用。在线性递减法中考虑最终均方误差直接决定初试训练精度故采用式(8)进行惯性系数更新。

4 Adam与Ada Mod优化器模型

4.1 Adam算法优化器

Adam算法为Kingma与Ba在2015年提出。并且经过大量工程证明在非凸函数优化以及非线性问题中相对SGD有着更为优秀的表现。目前在深度学习以及自然语言处理中有着广泛的运用。

传统随机梯度下降(SGD)算法选用一个固定的学习速率对所有w、b按照一个维度进行更新。虽实际工程表现较好，但尚缺乏可解读性。ADam算法在SGD算法的基础上引入误差梯度的一阶与二阶指数加权矩阵以此为依据在迭代中根据模型的实际训练情况对各神经网络节点的w、b采取合适的η步长，w的修正可表达为式(8)：

(8)

式中，β惯性系数；m、v为一阶与二阶动量项；g为均方误差。η初始学习率。τ正则化常数量默认为108作用为限制修正量。t为当前次数。采用Adam算法优化器进行模型训练可以得到如图7训练结果。

随着迭代的进行，采用Adam算法基于式(8)对神经模型进行参数更新可有效降低训练集误差，对样本特征进行有效学习，最终在固定105迭代次数下累计训练集误差为0.375综合考虑测试集样本数量，训练效果良好。使用测试集样本对模型进行泛化性测试如图8所示。

图7 Adam算法训练误差 图8 Adam算法预测

由图8可知模型在20个训练集样本之下累计绝对可控制在0.5 μm之下结合python工作台可知误差最大项为0.031 μm。综上有理由相信Adam可有效作为表面粗糙度神经网络预测模型的优化器。且相对SGD算法，Adam在神经网络参数更新过程中对步长的调整以及梯度修正量更加具有针对性，一般来说当参数设置合理时可以使模型更快收敛且具有更好的拟合精度。

4.2 Ada Mod算法优化器

Ada Mod由北大孙栩课题组提出为Adam算法的一种改进，通过对参数的长期学习速率进行缓冲可使得模型在提高学习精度的基础上更快收敛。在T次学习迭代中设初始化参数θ；步长α为长度为T的向量；动量β1，β2为一阶与二阶动量M、V对应的惯性系数；设代价损失函数ψ,正则化常数τ,则可得图9算法流程。

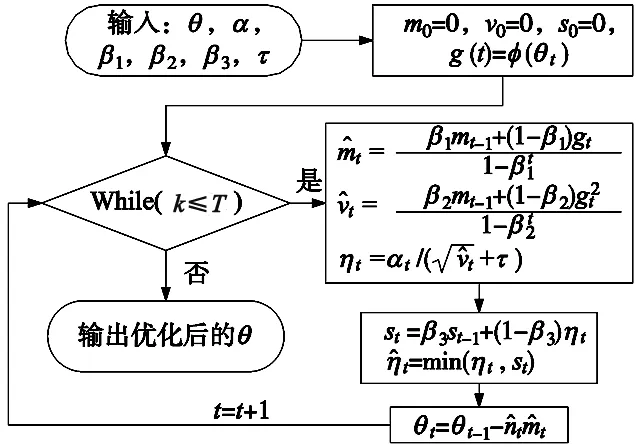
图9 Ada Mod算法流程

替换表3中θ为w、b即可得到神经网络参数更新公式。对比章节4.1及式(8)可知Ada Mod在迭代中增加超参数β3对训练中参数记忆长短进行了记录，可有效避免Adam算法在自适应学习时初期即使有正则化系数τ进行限制依旧会导致学习率过大导致学习异常的现象。且具有RAdam算法的特征无需进行预热开始训练时便具有一定的算法稳定性。选择同样的测试指标可得如图10所示。

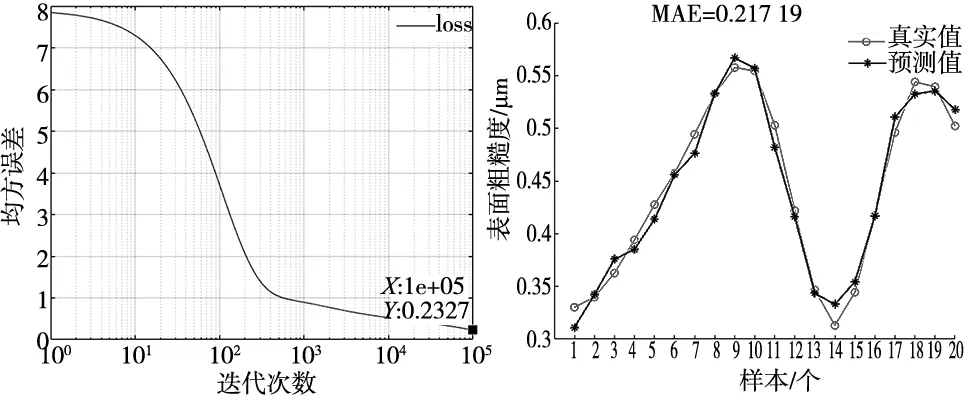
(a) Ada Mod算法训练误差 (b) Ada Mod算法预测图10 Ada Mod算法

结合图7、图8、图10,可以直观发现Ada Mod优化器无论在训练集误差还是测试集误差上均相对Adam有着更好的表现。且最终测试集累计绝对误差可以控制到0.02 μm，各项平均误差为0.001 μm，误差最大项为0.023 μm。有理由相信作为一种新的算法优化器Ada Mod不仅可以在卷积神经网络、自然语言处理模型上对模型有效训练，在表面粗糙度预测模型上也有着十分优秀的表现。

5 总结

(1)基于Xavier的粒子群优化算法进行神经网络初始化相对传统传统PSO-BP可以有效降低神经网络模型的初始均方误差，获得更好的初始化状态。

(2)Ada Mod算法优化器通过对Adam进行算法改进，在神经网络预测模型中可使模型参数更新更加有效，有效降低训练集误差，并提高模型预测能力。