基于结构权重的三维模型动态约简方法的研究*

欧阳会东，吴文江，胡 毅

(1.中国科学院大学，北京 100049 ；2.中国科学院沈阳计算技术研究所，沈阳 110168 ；3.沈阳高精数控智能技术股份有限公司，沈阳 110168)

0 引言

随着“中国制造2025”和“工业4.0”在国内的提出，工业生产的数字化建设也愈发重要。近年来，虚拟现实、数字孪生等技术的迅速发展也为数字化建设提供了强大的技术支持[1-3]。计算机硬件水平虽然在高速的发展，但是虚拟三维模型的渲染速度也在随着用户对模型精度的要求的提高越来越无法满足需要。针对3D场景中模型的渲染，国内外学者提出了很多不同的解决方法，如细节层次模型LOD(Level of Detail)技术，基于GPU的渲染加速技术等[4-6]。上述方法虽然较大的提升了模型的渲染速度，但是上述方法都是对三维模型的整体进行渲染。针对复杂度高，子结构较多的三维模型，仍然存在渲染速度过慢，GPU和内存占用率过高的问题。

本文通过研究三维模型的结构特征，发现三维模型在不同的视点距离下，部分结构的渲染对模型整体真实度的影响较小，这部分模型结构对模型整体真实度的影响因子很低。根据模型子结构相对于模型整体的体积比例不同，随着视点与模型的距离变化，可以动态的计算各个子结构的渲染度，通过与渲染阈值进行比较，可以避免对影响因子较低的结构进行渲染。该方法可以较为明显的减小三维模型的渲染压力。能够在不影响模型整体真实度的情况下，提高模型的渲染速度，降低GPU和内存的占用率。

1 三维模型结构的权重系数的确定

本文是根据三维模型与视点的距离，确定不同结构的渲染程度。各个结构的权重系数可以通过以下3步进行确定：

(1)确定主要模型结构：主要模型结构为三维模型的暴露在视点范围内的结构。针对这部分结构，赋予较大的权重系数，即使模型与视点的距离很大，也能保证视点范围内模型的整体真实度。

(2)确定次要模型结构：次要的模型结构为不暴露在视点范围内的结构。这部分结构的渲染度会跟随视点距离模型的远近不断改变，从而动态的对模型结构进行约简。

(3)针对每一个模型结构相对于模型整体的的体积比，赋予模型结构不同的权重系数。当视点与模型的距离非常远的时候，细小的模型结构的渲染对模型整体的影响将会变得很小，此时可以放弃这部分结构的渲染，从而节省系统资源，提高渲染速度。

2 动态约简方法的实现

动态约简的实现主要分为三个方面：首先计算模型结构相对于整体的体积比，然后判断模型结构是否在视点范围内，并计算视点与模型之间的距离，最后计算模型结构的渲染度，通过渲染度与渲染阈值的比较，判断当前结构是否需要进行渲染，实现渲染过程中对模型结构的动态约简。

2.1 计算三维模型结构的体积

Unity3d引擎中，每一个模型都有MeshFilter组件，MeshFilter组件中又包含了Mesh属性。Mesh属性中记录了vertices(顶点数据数组)、triangles(三角形顶点索引数组)、normals(法线向量数组)、uv(纹理坐标数组)等信息。针对每一个模型都有MeshFilter(网格过滤器)属性。

图1 三维立方体模型图

为了计算三维模型的体积，首先我们需要取得三维模型所有顶点及三角面片的数据，Unity3d中提供了mesh.vertices以及mesh.triangle两个属性，分别为vector3型数组和int型数组。其中mesh.vertices存储的就是平面的顶点信息，mesh.triangles存储的是三角形的顶点绘制顺序。然后将计算的代码脚本挂载于需要计算体积的模型结构上。以一个三维立方体为例，如图1所示。

首先通过mesh.vertices获取当前模型的三角面片所有顶点顺序，然后根据渲染顺序计算每三个连续绘制顶点与中心坐标点组合而成的三棱锥的体积。Unity3d引擎中，每个模型自身的中心坐标点为(0,0,0)，假设三棱锥的三个连续绘制顶点坐标为分别为(x1,y1,z1)，(x2,y2,z2)，(x3,y3,z3)。根据坐标向量即可通过行列式计算三棱锥的体积，即空间坐标系中的三棱锥的体积计算公式如下所示：

(1)

最后统计所有三棱锥的体积之和，即可以得到当前三维模型结构的体积。

2.2 视点范围的判断方法

Unity3d引擎中，与视点范围相关的坐标系分别为视口坐标系与世界坐标系。视口坐标系用于描述整个渲染画面的坐标，左下角为(0,0)，右上角为(1,1)。世界坐标系为整个渲染场景的坐标系，可以通过transform.position()函数获取。为了判断模型是否在视点范围内，首先需要判断当前模型在视窗的坐标是否在视口坐标系的范围类，然后通过点积运算判断模型是否在摄像机的前面，最后根据上述的计算结构即可确定模型结构是否在视点的范围内，详细的流程如图2所示。

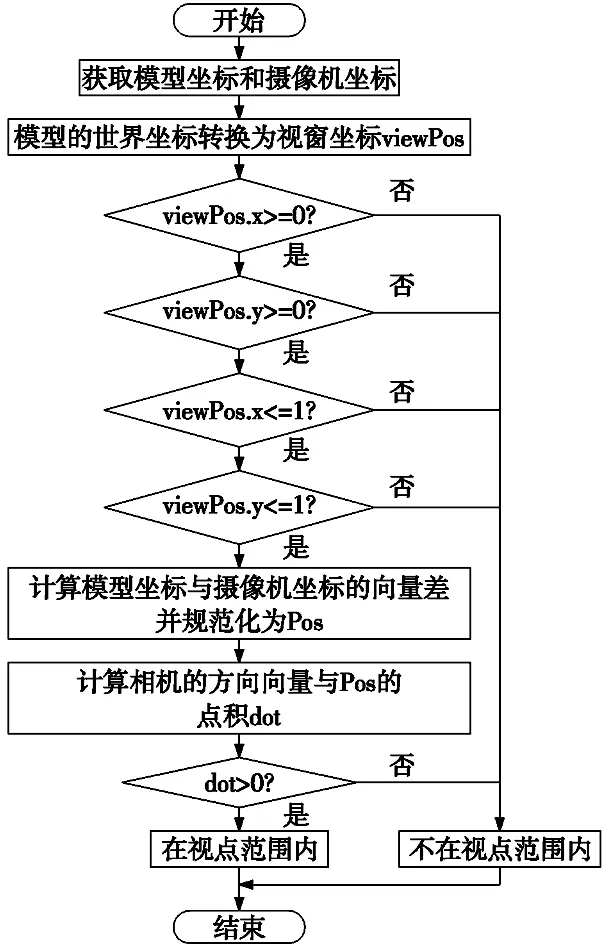
图2 视点范围判断流程图

2.3 视点与模型之间的距离

本文主要通过Unity3d软件进行研究及实验。距离的计算采用的是Unity3d软件自带的Vector3.Distance函数，调用该函数可以计算出视点与模型之间的距离L(单位为m)，函数伪代码如下：

float L=Vector3.Distance(transform1.position, transform2.position)

2.4 渲染度计算

本文算法在判断三维模型的某个结构是否渲染主要考虑两个因素，一个是该结构的体积Vi，另一个是视点与该模型之间的距离L，通过以上因素提出了渲染度以及渲染阈值的概念 。其中渲染度S定义公式为：

(2)

其中，当前模型结构在视点范围内时P的值为1，否则为0，σ为视点范围内模型结构的权重系数。ρ为体积占比的权重系数。

针对每一个三维模型，设置一个渲染阈值M，并通过 Renderer.enabled 属性控制其渲染。根据公式(1)计算该结构的渲染度。当结构渲染度小于阈值的时候，该结构在通过脚本控制取消渲染。只有结构的渲染度大于或等于渲染阈值的时候，脚本才将其渲染出来。根据不同计算机的硬件条件，可以设置不同精度的σ和ρ，σ和ρ越大，渲染的模型精度越高，随着距离的增大，渲染的模型结构数量越多。也可以宏观的调节渲染阈值M的值，对所有模型结构的渲染进行统一控制。

3 实验分析

3.1 实验环境

实验主要工具为Unity3d软件，硬件配置如表1所示。

表1 硬件配置表

3.2 实验过程与结果

为了验证基于三维模型结构权重的动态约简方法，使用不同三角面片数量的模型进行实验，下图为采用的实验模型示意图，其中图3为实验所用的模型结构透视图，图4为模型实体图。

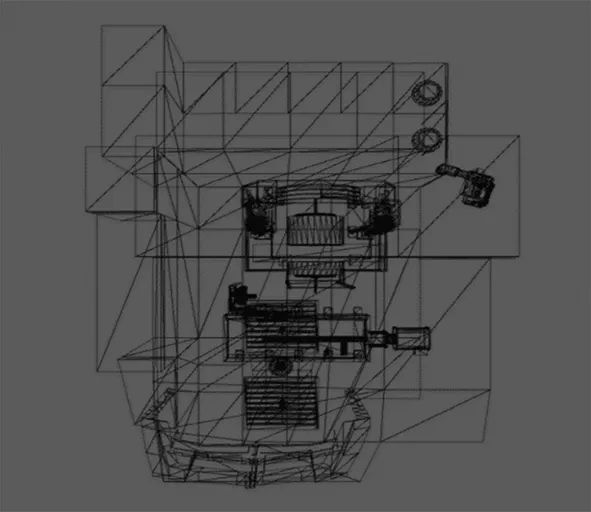
图3 模型结构透视图

图4 模型实体图

该模型总计有547个子结构，216 802个三角面片，通过多次实验，不断调整参数的数值，实验最终设置视点范围内模型结构的权重系数σ为100，体积的权重系数ρ为1，渲染阈值M为0.75， 然后对模型的结构进行体积计算并赋予相应的权重。通过调整视点与模型的远近，记录当前场景中的三角面片数量，帧率以及此时视点与模型之间的距离。表2为记录的主要实验数据。

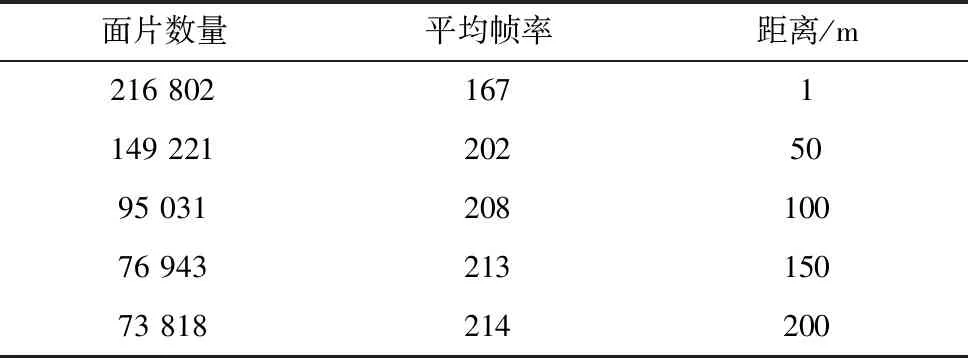
表2 面片数量变化表

为了验证方法的通用性，同时对三个不同三角面片数量的三维模型进行渲染，并绘制出三角面片数量根据距离的变化的折线图，如图5所示。其中纵轴为三角面片数量，横轴为视点与模型之间的距离 。

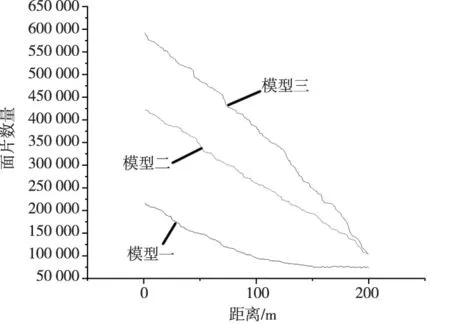
图5 三角面片数量变化折线图

由折线图可以观察到，模型在视点与其距离逐渐增大的过程中，三角面片渲染的数量在逐步降低。并且随着距离的进一步增大，开始趋向于一个稳定数值，这样距离过大时也保证了模型在视点范围内不会消失。

在上述研究的基础上，将该方法应用到虚拟现实场景中。通过对比试验论证该方法的实用性，并绘制距离与FPS(画面每秒传输帧数)的变化图。其中实验1为不使用三维模型动态约简方法，实验2使用了三维模型动态约简方法。

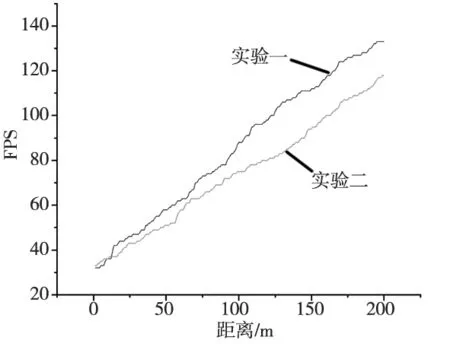
图6 实验结果对比图

实验结果显示，三维模型动态约简方法的应用，大幅度提升了虚拟现实场景渲染的流畅度，随著视点与三维场景的距离的增加，系统整体的FPS不断在上升并逐渐趋于稳定。其中使用了三维模型动态约简方法的实验2的FPS随着距离的增加一直高于未使用该方法的实验1。

4 结论

虚拟现实、数字孪生等技术一直是很多国内外学者研究的重点。三维模型作为这些技术的基础，针对三维模型的简化也有很多不同的方法。本文提出了基于模型结构权重的三维模型动态约简方法，该方法首先计算了模型结构的体积，模型结构与视点之间的距离，并判断当前模型结构是否在视点范围内，然后通过渲染度公式计算每个模型结构渲染度，最后通过渲染度与渲染阈值的比较，通过脚本控制当前模型结构的渲染。 该方法针对复杂的三维模型以及大型三维场景的实时渲染，在保证模型真实性的前提下，大幅度减少了三角面片的渲染数量，提高了模型的渲染速度，保证了三维场景渲染的流畅度，通过对比实验，在距离达到100 m以上时，三维场景的渲染帧率有了显著提升。 同时本文所提出的渲染度公式中加入了人工调整的控制参数，针对不同硬件配置的机器，调整不同的参数大小，保证了硬件配置较低的计算机同样可以快速渲染模型及三维场景，赋予了该方法更多的灵活性与适用范围。