基于响应面法的玻璃钻孔支撑结构优化设计*
2021-03-01王欣欣李中凯刘等卓
王欣欣,李中凯,刘等卓
(中国矿业大学机电工程学院,江苏 徐州 221116)
0 引言
玻璃磨边钻孔一体化设备是目前小微玻璃加工企业广泛使用的玻璃加工设备。钻孔模块作为磨边钻孔一体化设备的关键模块之一,其钻孔质量直接影响到产品的合格率。为了提高钻孔质量,孙建章等[1]通过对金刚石环形钻头的倒角尺寸、形状及外加载荷与钻孔质量关系的研究,获得了提高钻孔质量的最佳倒角参数及外加载荷。魏海波等[2]通过研究钻孔控制方式提高了钻孔效率,改善了钻孔质量。然而,钻孔质量不仅受到钻孔参数、控制方式等因素的影响,钻孔支撑结构的变形也是影响钻孔质量的重要因素。钻孔支撑结构的变形会引起玻璃钻孔处产生裂纹,严重影响产品的合格率。
利用响应面法进行结构优化设计是近年来结构优化领域研究的热点,可以有效的减小传统优化设计计算量大、耗费时间长的缺点。Lee J J等[3]采用响应面法优化了板料的结构参数和工艺参数,提高了板料成型的质量;张雷等[4]基于响应面法获取了最佳柔轮设计参数。为了获取精度更高和计算量更小的响应面模型,国内外学者采取了改善选点策略[5]、改进内插公式[6]、局部样本点加密[7]、平移、缩放优化区域[8]等方法来改善响应面。然而,对于某一特定问题,采用何种响应面模型并没有先验知识。本文先后采用了两个不同的响应面模型,并通过响应面合理性评估选择了较优的一种,然后采用NSGA-Ⅱ获取了钻孔支撑结构最优设计尺寸,此方法对钻孔支撑结构的改进有一定参考价值。
1 有限元模型的建立
1.1 钻孔支撑结构三维模型的建立
玻璃磨边钻孔一体化设备可用于对不同尺寸的圆形玻璃进行磨边和钻孔加工,其结构示意图如图 1所示,分为滚道模块、上片模块、机械手模块、磨边模块、钻孔模块、第三孔位钻孔模块、下片模块和动力模块等。首先,玻璃经滚道模块运输至上片模块,其次由上片模块传递给机械手模块,机械手模块先后将玻璃运送至磨边模块和钻孔模块进行磨边和钻孔操作,最后经下片模块运输至下一道工序。此设备可用于加工直径在140~380 mm,孔距为32~120 mm的圆形玻璃。

图1 玻璃磨边钻孔一体化设备
钻孔模块的结构示意图如图 2所示。钻孔模块由钻孔支撑结构、机头总成(直流无刷电机、步进电机、齿轮箱、钻头和机头总成底座)、夹紧气缸、动夹板和动夹板支撑结构组成。当玻璃经机械手运送到钻孔模块时,夹紧气缸推动夹板将玻璃夹紧,一侧步进电机带动直流无刷电机先后进行快速进给、中速钻孔、慢速倒角和快速回退;快速回退的同时另一侧重复同样动作,从而实现玻璃的两侧钻孔。钻孔支撑结构示意图如图 3所示,由夹板、横梁、立柱和底板焊接而成,材料为Q235普通碳素结构钢。

图2 钻孔模块 图3 钻孔支撑结构
1.2 受力分析
钻孔支撑结构主要受到玻璃对夹板的推力、步进电机对横梁的推力、直流无刷电机钻孔时产生的扭矩、机头总成的重力和机架对底板的支撑力。
玻璃对夹板的推力来自于夹紧气缸,如图 2所示,夹紧气缸推动动夹板将玻璃夹紧,夹紧气缸产生的推力大小等同于玻璃对夹板的推力,气缸为双杆气缸,缸径为20 mm,由式(1)可求得夹板受力大小。由应力、应变公式知,在受力不变的条件下,夹板受力面积越小,应力、应变越大,由于后续优化对象为最大变形,且约束为最大等效应力,因此受力面积取可加工的最小直径玻璃所对应的面积,如图 4所示区域A为该推力的受力区域。
(1)
式中,c=2,为夹紧气缸个数;k=2,为夹紧气缸的推杆数量;P=0.5 MPa,为工作压强;D=20 mm,为气缸缸径。计算得玻璃对夹板的推力为628 N。
步进电机对横梁的推力,与步进电机输出轴的转矩和步进电机输出丝杠的导程有关。由步进电机的矩频曲线[9]可知,随步进电机转速的增加,转矩逐渐减小,因此在对玻璃进行慢速倒角时支撑结构所受到的轴向力最大。由能量守恒定律可知,步进电机输出丝杆旋转一周所做的功与推动负载前进一个导程所作的功相同,即
T·2π=F·S
(2)
式中,T为实际工作时丝杠转矩,略小于静转矩,与步进电机转速有关;S为步进电机输出丝杆的导程,结合经验数值,求得钻孔时的轴向力约为600 N。作用于横梁槽与机头总成底座的接触面,即图4所示B、C区域。
直流无刷电机产生的扭矩等效到钻孔支撑结构后产生的作用较小,且不易计算受力点,此处忽略不计。
机头总成的质量为3.5kg,即35 N,作用于横梁上侧,即图4所示D、E区域。支撑力作用于底板,即图4所示F、G区域。

图4 钻孔支撑结构受力图
1.3 有限元仿真
首先,在SolidWorks中建立钻孔支撑结构的参数化模型,将其导入至Workbench中;其次,进行材料参数设置;最后,在Model模块依次进行接触设置、网格划分、载荷施加和模型求解步骤。求解得到钻孔支撑结构的等效应力和变形如图 5、 图6所示,最大等效应力为52.655 MPa,最大变形为0.43 mm,并查得质量为9.112 8kg。

图5 初始尺寸下钻孔支撑结构的等效应力

图6 初始尺寸下钻孔支撑结构的变形
2 响应面模型的建立
在进行机械结构优化时,需要建立机械结构的特性与设计参数之间的关系表达式。然而,在很多实际工程问题中,建立这种对应关系需要大量的数值分析和计算,而且很难得到明确的显式数学表达。改善这种情况的一个办法就是使用响应面法建立响应面模型,又称代理模型。
响应面法是一种采用试验设计理论对指定的设计点集合进行试验,得到目标函数和约束函数的响应面模型,来预测非试验点的响应值的方法[10]。其思想类似于“黑箱”原理,只需要确定输入与输出的对应关系,无需了解系统内部结构。响应面法是一种将数学方法和统计方法相结合的稳健技术,在工程实践中得到了广泛的应用[11]。响应面模型的建立包含试验点的选取、拟合函数的选择和响应面合理性评估三个部分。
2.1 试验点的选取

图7 CCD组成示意图
试验点的选取作为响应面构建的第一步,对响应面的精度有很大影响。不合理的试验点甚至导致构造不出响应面[12]。常见的试验设计方法有Central Composite Design(简称CCD)、Optimal Space-Filling Design(简称OSF)、Box-Behnken Design(简称BBD)等,本试验设计采用目前应用较为广泛的CCD。CCD由1个中心点,2m轴向点,2m-ζ超立方体的顶点(析因点)组成。如图7所示为设计变量为3时试验点的组成图,图中大圆,五角星,小圆分别代表中心点、轴向点和析因点。
设计变量m与试验点个数n的关系如表1所示。为了在满足钻孔支撑结构设计要求的前提下尽量扩大优化空间,选取了钻孔支撑结构的7个尺寸作为设计变量,分别为夹板厚度(D1),横梁厚度(D2),立柱厚度(D3),底板厚度(D4),夹板槽长(L1),夹板槽宽(L2),横梁槽长(L3)。7个参数的尺寸变动范围如表2所示。

表1 CCD设计变量与试验点个数关系

表2 设计变量的尺寸变动范围
由表1、表2可知,本试验设计将在7个设计变量的尺寸变动范围内选择79个试验点。在Geometry模块选中7个设计变量作为待优化参数,然后进入Response Surface模块中的Design of Experiment中选取设计变量的上下界,选择试验设计类型为CCD设计,点击更新即可产生79个试验点。
2.2 拟合函数的选择及响应面合理性评估
目前,较为常用的响应面模型有标准响应面模型(全二阶多项式)和Kriging模型。
标准响应面的函数表达式为:
(3)
式中,xi为设计变量,m为设计变量的个数,a0、ai、aii、aij为多项式的待定系数。
Kriging模型的函数表达式为:
(4)
式中,f(x)用于提供模拟全局近似;β为回归函数待定系数;z(x)用于提供模拟局部偏差近似。
对于某些特定问题,其具体目标函数并没有先验知识,因此也无法判断使用哪种响应面模型较为准确。如果处理的模型非线性程度较低,适合采用标准响应面模型,而对于高维和非线性程度较高的问题,则适合选用Kriging模型。在实际应用中可先取标准响应面进行拟合,经验证后若效果不佳,再进行另一种拟合函数的选择。
评估响应面合理性的常用指标有R2(决定系数)、RMSE(均方根误差)和RMAE(相对最大绝对误差)等:
(5)
(6)
(7)
为了更直观的判断响应面拟合的合理性,还可以在Response Surface模块内查看计算值与预测值关系图。预测值与计算值的关系曲线越接近于45°的直线,则证明预测的越准确;偏离45°直线较为明显的区域即为误差较大区域。此外,为进一步验证响应面模型的准确性,需要加入验证点进行验证。
试验点选取后在Response surface模块中选择标准响应面,建立7个设计变量与最大等效应力(σ)、最大变形(δ)和质量(m)关系的响应面。根据标准响应面拟合结果和实际计算值,可以得到如表 3所示标准响应面模型评估指标值。由于均方根误差和相对最大绝对误差指标值都较差,因此该模型不适合采用标准响应面模型进行拟合,需改用Kriging模型。

表3 标准响应面模型合理性评估
由于采用Kriging模型建立的响应面会通过所有试验点,因此需要添加验证点验证响应面模型的准确性。添加验证点后,根据Kriging模型拟合结果和实际计算值,得到Kriging模型合理性评估指标,如表4所示。

表4 Kriging模型合理性评估
由表4和图8可知,Kriging模型局部误差较大,依据图 8所示预测值与计算值关系图中验证点与45°直线的偏离程度,可查得局部误差较大区域,在局部误差较大区域添加新的设计点,即可改善误差较大区域的精度。经过两次细化,添加验证点后,验证点处的最大等效应力、最大变形和质量的均方根误差值分别为0.061 81、0.000 33、1.723E-08,相对最大绝对误差分别为0.848 92%、1.214 9%和0,细分后的Kriging模型具有较高的精度。

图8 Kriging模型预测值与计算值关系
3 钻孔支撑结构优化
3.1 优化数学模型
钻孔支撑结构优化的目的是提高钻孔质量,同时节省材料,降低成本。本文所涉及的优化模型将钻孔支撑结构的变形和质量的最小化作为优化目标,最大等效应力作为约束条件,建立的多目标优化模型如下所示:
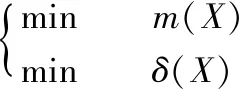
s.t. σ<[σ]

3.2 优化过程及结果分析
采用非支配排序遗传算法(NSGA-Ⅱ)对钻孔支撑结构进行优化,NSGA-Ⅱ于2002年由DEB K等[13]提出,被公认为最有效的多目标优化算法之一[12]。
基于Kriging模型建立的钻孔支撑结构的响应面模型,在Response Surface Optimization模块,设定目标为最大变形的最小值和质量的最小值,设定约束条件为最大等效应力小于235 MPa。初始种群为7000,每代产生1400个样本,经20次迭代后获得如图9所示的Pareto解和3个候选解。由于候选解1的变形量和质量均小于另外两个候选解,因此候选解1为较优解。

图9 钻孔支撑结构Pareto解
为了能获得适合工程应用的最优结果,应将优化结果进行修正。此时需要灵敏度分析,使修正的结果更好的满足优化目标,对于玻璃钻孔支撑结构,其结构变形将导致玻璃裂纹,严重影响产品合格率,因此依据最大变形的灵敏度进行修正,各设计参数对最大变形的灵敏度如图10所示。

图10 各设计参数对最大变形的灵敏度
由灵敏度分析图可知,最大变形与夹板厚度、横梁厚度、立柱厚度、底板厚度和夹板槽长成反比,与横梁槽长成正比,受夹板槽宽变化影响较小。按照与最大变形成正比的设计变量向下取整,与最大变形成反比的设计变量向上取整,对最大变形量影响较小的设计变量向减小质量的方向取整的原则,获得了如表5所示的修正解,将该修正解对应的钻孔支撑结构进行有限元分析,得到优化后的各目标值,填入表5,同时将原始尺寸和候选解1的各参数值填入表5。

表5 优化前后各参数对比
原始尺寸设计与优化后的尺寸设计相比可知,在满足最大等效应力小于许用应力的前提下,最大变形减小了57.1%,质量减轻了30.4%,达到了提高钻孔质量,降低成本的目的。
4 结论
(1)本文提出一种玻璃磨边钻孔机床的结构优化设计方法,在ANSYS Workbench软件对钻孔支撑结构进行分析的基础上,采用响应面法建立设计变量与性能目标之间的数学模型,采用多目标进化算法NSGA-II求解并选优,获得了优化的支撑结构质量和最大变形量的设计方案,证明了优化设计方法的有效性。
(2)通过设计试验证明,Kriging响应面模型具有比标准响应面模型更高的拟合精度,适合于多设计变量和非线性设计问题的拟合;响应面模型生成后,需采用响应面合理性评估验证模型的准确性。
(3)非支配排序遗传算法NSGA-II可对多目标优化问题进行高效求解和选优,并通过设计变量的灵敏度分析完成设计参数的取证运算;设计试验对比证明了所提出基于响应面法和NSGA-II的机床结构优化设计方法的正确性和高效性。
