机器学习辅助下的五轴数控铣削刀轨优化*

王小刚，邱 磊

(1.扬州工业职业技术学院交通工程学院，江苏 扬州 225127; 2.宁波工程学院机械工程学院，浙江 宁波 315336)

0 引言

在铣削加工过程中，必须有效确定切削速度和进给速度等工艺参数，以及切削宽度和切削深度等几何参数。计算机辅助制造(CAM)系统可以根据这些参数和零件模型，从而为机床生成一条刀具路径。然而，在随后的铣削加工过程中，由于切削条件不恒定，例如刀具的接近和后退、零件的轮廓[1]和机床轴的物理限制[2]等原因，不可避免地会出现非恒定的切削条件，导致刀具挠度发生变化。但是，真实制造环境中制定切削工艺和验证的成本均较高，尤其是进行单件生产和小批量生产时。

因此，为了分析和计划切削过程，研究人员开发了许多经验和分析模型[3-8]。杨军等[9]使用了刀触点综合离散方法,解决了环曲面金刚石切削加工困难的问题，有效减少了离散误差，改善了工件的加工质量。但是这种基于模型和经验的方法大都存在适用性、鲁棒性不强的问题。针对上述问题，García-Ordás M T等[10]开发了一种使用前馈人工神经网络的方法，该方法能够根据切削模拟的结果进行训练。并使用训练后的模型预测当前加工工艺过程的稳定性，实现了用于切割过程的实时稳定性监控系统。

随着人工智能技术的发展，机器学习技术及其各种结合应用层出不穷。杨光美等[11]采用机器学习技术中的支持向量机方法，建立了超声振动磨削放电加工预测模型，其工艺指标预测值与试验值具有较好的一致性。Yang L等[12]对切削加工领域中机器学习技术的应用进行了分析，并强调了基于生产过程的机器学习系统的强大能力和巨大潜力。

为了改善现有数控铣削加工机制,以进一步提高加工精度并实现自寻优控制，本文采用机器学习技术提出了一种用于五轴数控加工的刀轨自优化方法。该方法能够根据已有的工艺自动生成必要的工艺知识，并进行自优化和生成刀具路径。在五轴CNC加工机床上进行了具体应用测试。

1 刀轨自寻优控制原理

为了获得独立于工件(与工件无关)的工艺知识，设计了一个铣削加工材料去除反馈闭环控制方法，如图1所示。

图1 用于刀具路径规划自优化的反馈环路

该铣削加工材料去除仿真系统是轴驱动的，并且可以将计算出的切削条件直接与相应的形状误差测量相关联。通过机器学习对切削条件和形状误差之间的关系进行建模，可以不断产生技术知识。所获得的知识将应用在CAM过程中，以预测新零件的形状偏差。本文重点介绍了该方法在五轴铣削中的实现。此外，重点分析了所获得知识的可传递性。最后，对形状误差自动补偿进行了分析。

2 建模与刀具轨迹优化方法

2.1 仿真建模

铣削加工材料去除过程中，需要计算空间切削条件以获取实际进给速度、材料移除率和实际铣削过程中的切削深度。因此，切割过程分为基本、重复和独立于工件的部分。为此，将标准PC通过以太网连接到机床的内部网络，并以250 Hz的恒定采样率定期读取轴坐标信息，如表1所示。

表1 轴坐标数据参数

在对五轴机床进行建模时，旋转轴相对于之前的位置至关重要。对于每个轴位置样本，执行如下仿真步骤：首先，将轴数据流中的轴位置分配给虚拟轴。因此，刀具和工件位置将相应地发生变化。然后，计算刀具和工件的交点并进行材料移除。在这项研究中扩展了工件的dexel数据模型，因此可以将计算出的切削条件存储在dexel端点中。这是通过为每个修改后的dexel端点指定最新的切割条件来实现的。该刀具表示为圆柱体。仿真与加工过程同时进行，即并行作业。图2为模型计算的可视化图。

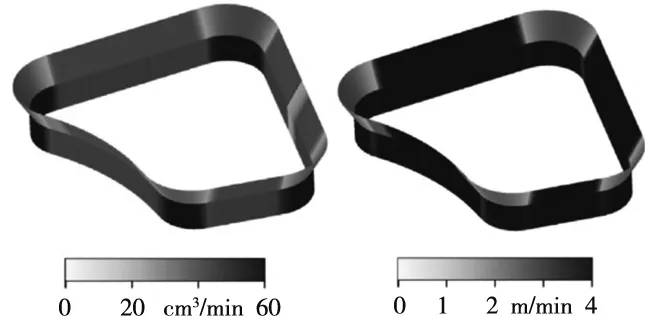
(a) 物料移除率 (b) 进给率图2 模型计算的可视化图

2.2 检测与机器学习方法

形状测量使用了Blum TC52接触式测头。通过进行测量，可避免因坐标变化而造成的潜在误差。测量程序是从虚拟机加工的dexel模型而自动得出的。为了确保将测量的形状偏差分配给单个dexel，需要在单个dexel端点的精确位置上对工件进行采样。确定表面的垂直方向，并确保垂直于表面时进行测量。得到带有测头的测量值，标记所研究的dexel，并在测量值和单个dexel之间建立关联。每次测量后，将测量点加载到工件模型中，然后计算到标记dexel端点的距离。该距离垂直于表面，被称为形状偏差ds：

(1)

式中，(xd,yd,zd)为dexel端点的坐标，(xm,ym,zm)为相应测量点的坐标。

本文提出的方法利用回归模型来预测CAM系统内加工过程的结果。回归方法的总体目标是估计函数f[11]：

Y=f(X)+ε

(2)

式中，Y为函数结果,X为函数输入,ε为随机误差, 该f反映三者之间的关系。应用于预测形状偏差的任务时，X可以用下式表示：

(3)

式中，f为进给速度、QW为材料去除速度，dth为沿刀具轴的表面点到工具中心点位置(TCP)的投影距离。并且Y表示为：

Y=ds

(4)

统计学习方法使用训练数据来获得对关系建模的回归函数。使用先前过程的数据集进行训练时，可以建立学习机制。一种有效的统计学习算法是支持向量机(SVM)[11]。SVM的基本概念是确定分隔训练数据的超平面。通过引入合适的损失函数，可以将SVM 方法应用于回归问题。SVR已成功应用于各种工程问题。本文重点介绍了SVR在预测侧面铣削变形方面的应用。

通过本文的方法，可以使用SVR根据先前计算的空间切削条件将形状误差预测分配给工件模型的每个dexel端点[11]。为了获得独立于组件形状的模型，仅将与形状无关的特性用于机器学习。提供的特性包括f、QW和dth。本文SVR模型使用了LIBSVM开源库[12]。

2.3 刀具轨迹优化

可以利用仿真的结果来预测不同切削条件对偏差的影响，并选择合适的参数来满足公差要求。此外，预测的偏差可用于优化刀具姿态来减少形状误差。工艺仿真不仅计算每个仿真步骤的切削条件，还提供TCP和刀具方向作为工件坐标系中的方向矢量。通过预测每个仿真步骤中修改后dexel端点的形状偏差，可以实现刀具路径优化：首先，TCP沿着垂直于进给矢量和刀具矢量的方向移动一个仿真步骤的最小偏差；其次，将转换后的TCP和未修改的刀具矢量写入NC文件；最后，补偿后的NC程序可以直接由机器控制执行。图3显示了优化后的刀具路径。

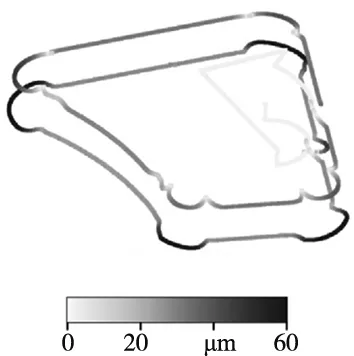
图3 刀具轨迹优化

3 实验结果与分析

3.1 实验配置

为了对所提出的方法进行分析，选择了车轮架的两个凹腔进行加工实验。两个凹腔的壁面形状都由一个垂直部分和一个30°倾斜部分组成，如图4所示。

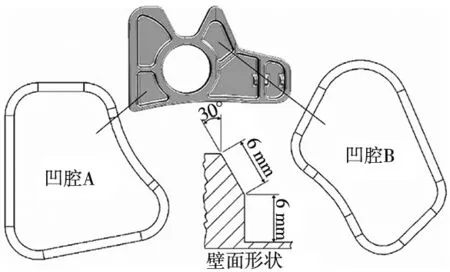
图4 五轴测试零件

垂直部分是通过三轴外围铣削过程进行加工的，而倾斜部分则需要进行五轴铣削。工件材料是高强度铝。在进行精加工之前，所有凹腔的轮廓都要经过粗加工。最终形状的偏移量设置为1 mm。

精加工过程使用硬质合金立铣刀(D=6 mm)。刀具路径由Siemens NX 11.0生成[13]。精加工时的切削深度设置为6 mm，切削速度设置为400 m/min，每齿进给量设置为0.04 mm。所有操作均在配备了Siemens 840d控制器的DMG HSC 30线性五轴加工中心上进行，实验测试装置如图5所示。

(a) 五轴加工中心 (b) 铣削加工现场图5 五轴机床实验装置

3.2 学习行为分析

为了评估学习行为，加工了9个凹腔A的样本。每三个样本更换一次刀具，以限制刀具磨损的影响。第一个样本的选定点用于训练SVR模型。 接下来，将模型应用于预测第二个样本的形状偏差。然后，比较第二个样本的预测和测量的形状偏差，并计算均方根误差(RMSE)作为预测精度的量度。验证数据集由样本的所有测量点组成，因此其大于特定的训练数据集。然后使用第一部分和第二部分的样本训练模型并预测第三部分的形状偏差，依此类推。所有先前样本的组合知识可用于预测后续样本的形状偏差。SVR模型的RMSE的结果如图6所示。

图6 RMSE结果

可以看出，采用这种方法时，模型预测精度几乎与加工样品的编号无关。需要注意到，测量点增加时通常会造成平均RMSE降低。当选择n=64或n=125个测量点时，可获得最佳模型精度。所获得的模型对于重复的过程有效，并且使用新刀具时不会显示出明显的偏差。预测和测量之间的高度相关性表明，可以使用该方法根据五轴加工中的模拟切削条件来预测形状误差。

3.3 知识的可传递性分析

具有知识可传递性的模型在一定程度上可以应用于不同几何形状(具有相似特征的)。为此，需要检查凹腔B的铣削过程。根据凹腔A生成刀具路径，并使用根据凹腔A信息生成的模型对空间误差进行预测。加工凹腔B的三个样本并在100个随机选择的点处对其进行研究。接下来，将这些点的测量形状偏差与相同位置的预测形状偏差进行比较，结果如图7所示。

图7 凹腔B形状偏差的测量与预测

所测量和预测的形状偏差具有较高的相关性，其相关系数为r≈0.937。所有的预测值与相应的测量值的差都在13 μm的范围内。由此得出结论，通过参考局部切削条件，可以将训练后的模型应用于具有可比较特征的形状不同的凹腔。

3.4 刀具路径优化结果分析

为分析补偿的效果，对三个带有凹腔A和凹腔B的工件进行了加工处理，并在200个随机选择的点上对每个样品的表面进行了研究分析。将补偿凹腔A之前/后测得的形状偏差归集到bin中。图8中的直方图显示了每个bin的相对频率。

图8 对凹腔A进行补偿前/后的测量形状误差

发生偏差的范围代表了重要的信息，因为它对应于最大形状偏差。因此，从图8可以看出，当对过程进行补偿时，最大的形状偏差在凹腔A处从70 μm减小到35 μm，降低了50%。根据凹腔A的信息生成一个模型，利用这个模型得出凹腔B的优化刀具路径。图9显示了对凹腔B的补偿效果。

图9 对凹腔B进行补偿前/后的测量形状误差

可以注意到，形状偏差的减小与凹腔A相当。因此，可以将过程知识用于准确预测和补偿新几何零件的形状偏差。综上所述，从第一凹腔获得的模型可以高精度地应用于不同形状的第二凹腔。预测的形状偏差还用于优化刀具路径，以最大程度地减小形状偏差。

4 结论

本文提出了一种生成自优化刀具路径的方法。该方法使用了基于加工材料移除仿真和机器学习的自主知识获取。通过五轴加工两个凹腔进行了测试。得出如下结论：①提出的刀具路径优化方法可以将最大的形状偏差降低50%；②通过评估传递性，验证了提出方法具有知识的可传递能力。在将来的研究中应考虑时变效应(例如刀具磨损)，以提高预测质量。