基于图优化的轴承内外径尺寸检测*

陈甦欣，韩 暑，涂德江，晏文彬

(合肥工业大学机械工程学院，合肥 230009)

0 引言

轴承是各类机械设备的重要基础零部件，随着现代工业的快速发展，对轴承的精度和寿命提出了更高的要求[1]。轴承的几何尺寸是生产加工中非常关键的参数，传统的尺寸检测方法大部分是通过游标卡尺、千分尺等进行接触式测量获取轴承的几何尺寸，具有精度低、效率低、且易引入人为误差的特点，不再适应现代化的生产需求。

目前改进的轴承尺寸检测技术有很多，包括超声波探声法，激光扫描法以及视觉检测法，其中超声波和激光检测方法具有较好的检测效果，但成本较高。视觉检测法具有非接触、动态范围大及信息丰富等优点，解决了传统检测方法精度低、劳动量大、工作效率低等问题。刘科文等[2]使用了最小二乘法拟合边缘像素，可以获得轴承的内外径尺寸，但是达不到高精度的要求。GAO Y等[3]采用了轴承侧面投影方法检测轴承的外径尺寸，但无法应用于轴承的内径尺寸检测。朱福康等[4]提出了一种基于图像深度信息集的Hough圆检测方法，对轴承进行了边缘特征提取。该方法具有对噪声不敏感的优点，在一定程度上提高了轴承尺寸检测的精度，但是需要在参数空间进行累计，计算量较大。为了解决这一问题，本文重点研究了一种基于g2o(图优化)的尺寸检测优化方法，该方法具有高精度、高效率的特点，很好的解决了轴承在检测过程中精度与时间复杂度协调的问题。

1 图像预处理及像素级边缘检测

图像的信号在形成及传输的过程中夹杂着各类的噪声[5]，需要对图像进行滤波处理以降低噪声。常用的滤波处理有高斯滤波、均值滤波及中值滤波等。为了达到去噪保边的目的，使用双边滤波[6]对图像进行滤波，处理后的图像如图1所示。

图1 双边滤波及局部放大图

为了简化或改变图像的表示形式，需要对图像进行分割[7]。首先，使用阈值分割将灰度图像转换为二值化图像，再使用形态学操作排除图像中小型黑洞，结果如图2所示；其次，对二值化图像中所有连通域的面积进行计算，通过设置阈值剔除小于该面积的连通区域，得到最终的感兴趣区域图像如图3所示。

图2 阈值分割 图3 连通域处理

边缘检测技术的精确度直接影响测量结果的好坏。常用的像素级边缘检测算子有Laplacian算子、Sobel算子、Roberts算子和Canny算子等[8]。其中，使用Canny算子进行像素级边缘检测的效果较好，如图4所示。

图4 Canny边缘检测效果图

2 亚像素边缘检测

轴承尺寸检测对精度要求很高，故考虑亚像素级别的边缘检测。Zernike矩法是一种常用的亚像素边缘检测方法，图5为亚像素边缘检测模型，其中直线L与圆相交的弦代表理想边缘，b和b+n为边缘两侧的灰度值，d为原点到L的垂直距离，图6绕原点逆时针旋转θ度得到图7。

图5 原始边缘示意图 图6 旋转后边缘示意图

利用Zernike矩旋转不变性[9]可以计算出n,d,θ，若像素点满足n≥τ∩d≤δ，将像素点代入亚像素边缘点坐标计算公式：

其中，(x′,y′)为亚像素边缘点坐标，(x,y)为像素边缘点坐标，N为卷积核的大小，δ通常设置为单个像素长度的0.707。τ作为人工选择的阈值，其大小对图像边缘的判断具有十分重要的影响，如果τ取值过小，会检测出很多伪边缘，相反，若τ过大，真实边缘会被丢失，所以需要反复调整才能取得较理想的检测结果。图像的灰度值和阶跃灰度值在同一像素点处具有相同的变化趋势，可以利用Otsu法计算目标和背景基于阶跃灰度的最大类间方差，求得最优的阶跃灰度阈值τ，更快的完成检测过程。

3 基于g2o的曲线拟合方法

在机器人领域和计算机视觉中,许多优化问题最后都归结于求非线性误差函数的最小值问题[10]，通常对非线性最小二乘问题的求解有一些标准的方法，如Gauss-Newton(GN)和Levenberg-Marquardt(LM)等。然而，这些解法在求解的过程中需要进行大量的矩阵运算，使用g2o可以简化求解的过程。g2o是一个通用的图优化开源框架，该框架集成了Eigen矩阵计算库，具有强大的算力，部分框架如图7所示。

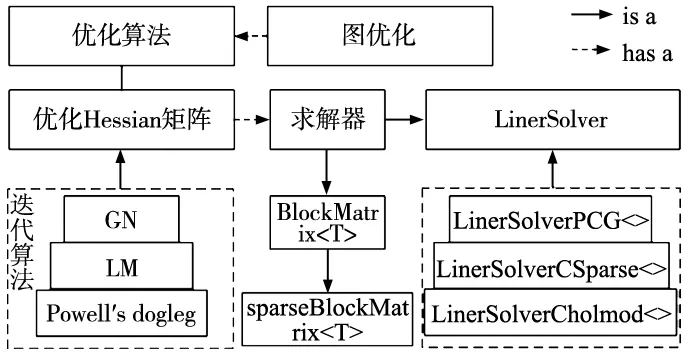
图7 g2o的部分框架图

从图7中可以看出，优化算法可以调用两个求解器，其中SparseBlockMatrix用来计算Jacobian和Hessian矩阵，linearSolver是用于线性方程求解。用户可以根据具体的误差函数选择合适的迭代算法，并对迭代算法中的参数进行调整，从而方便、快速地求解非线性最小二乘问题。本文在选择求解器与迭代算法进行曲线拟合时，由于迭代算法初始值的设置及异常数据的存在，导致优化算法并不稳定，因此，需要设置合适的迭代初始值并对异常数据进行适当处理。

3.1 选择迭代算法

通常最小二乘问题可以表示为：

对上式进行泰勒公式展开，保留一阶梯度得：Δx*=-JT(x)，称为最速下降法；若保留二阶梯度得：HΔx*=-JT(x)，称为GN法。最速下降法和GN法虽然直观，但在实际运用中最速下降法收敛速度比较低，GN法需要计算复杂的Hessian矩阵，计算结果不稳定。相比较而言，LM算法引入信赖区域思想，认为近似只在一定范围内成立，如果近似太小，则缩小范围，反之，则增加近似范围，保证了其增量方程的正定性；但是本文在使用该算法进行优化时发现算法的稳定性不是很好，主要是因为非线性优化的所有迭代求解方案，都需要提供一个良好的初始值，不同的初始值往往会导致不同的优化结果。因此，为了避免LM算法容易陷入局部极小值，在运行迭代算法之前，随机选择三个坐标使用最小二乘法拟合曲线方程，为LM算法提供变量的初始值，从而提高算法的稳定性。

3.2 处理异常数据

最小二乘法使用了平方函数衡量偏差[11]，使得异常数据的出现对最小二乘法的优化结果产生了破环性的影响，使用鲁棒性代价函数可以减少异常数据对误差函数的影响。常用的鲁棒性代价函数有Huber 函数，具体形式如下：

该函数可以将误差大于或等于阈值b的数据点按照线性增长而非二次增长，但是该函数并没有完全消除异常数据对优化结果的影响。于是，针对本文中出现的异常数据做以下分析处理：

(1)若异常数据使用Huber函数处理后，对最终优化结果的影响在容错范围内，则无需对异常数据做进一步处理，优化算法结束；

(2)若异常数据使用Huber函数处理后对最终优化结果影响较大，则需要对异常数据进行二次处理，优化算法继续进行；使用迭代算法得到的曲线方程，把所有的数据代入这个曲线方程求得残差后，通过设置容限误差来区分inliers和outliers，从而剔除异常数据。最后，对筛选后的数据再次使用迭代算法，可以得到较好的优化结果。

3.3 使用g2o优化曲线

本文曲线拟合的误差函数为：

上式，待估计变量(a,b)为圆心坐标，c为半径；(xi,yi)为亚像素坐标。

为了使用 g2o，需要将曲线拟合问题抽象成图优化。该图由若干个节点，以及连接着这些节点的边组成。其中，节点表示优化变量，边表示误差项。在曲线拟合问题中，整个问题只有一个节点，该节点包含曲线模型的3个参数a、b、c，而每个带噪声的数据点，即图优化的边，构成了一个个误差项。该边是一元边 ，即只连接一个节点，如图8所示。

图8 g2o曲线拟合模型

在g2o中建立该模型进行优化，步骤如下：

(1)定义节点和边的类型；

(2)构建图；

(3)异常边判断与处理；

(4)选择迭代算法；

(5)调用 g2o 进行优化,返回结果。

通过代码编程，优化模型构建，可以得到轴承内外径拟合部分优化过程参数，如图9所示，包含每次迭代时间、添加边的个数、总的迭代次数与时间以及尺寸参数，拟合优化结果如图10所示。

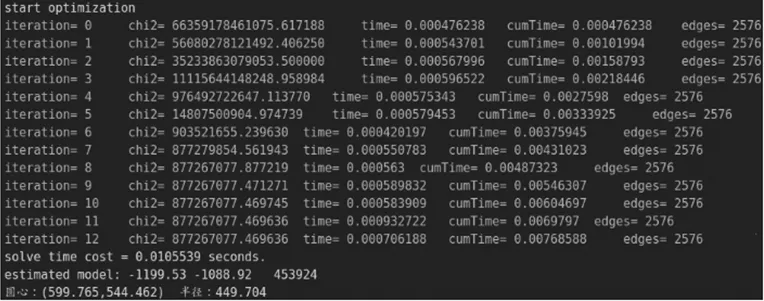
图9 轴承内外径拟合部分优化过程参数

图10 轴承内外径拟合优化结果

4 流程分析与实验验证

4.1 尺寸检测流程分析

尺寸检测主要分为图像预处理、边缘检测、内外点筛选、异常数据处理、使用g2o优化曲线5个部分，如图11所示。

图11 基于 g2o(图优化)的尺寸检测优化方法

4.2 实验验证

仿真实验在Linux环境下进行，CPU采用Intel Core i7处理器，内存为8 GB，编程语言采用C++。为了证明方法的有效性，在Visual Studio环境下使用基于g2o(图优化)的优化方法对轴承图像进行内外径尺寸检测，对轴承尺寸检测系统的精确度及时间复杂度进行评估。

精确度是验证方法效果的主要准则，精度的好坏会直接影响方法的测量结果。本文使用同心度、平均值及标准差来衡量检测精度，其中同心度表达式为：

其中，(x1,y1) 为轴承的外圆圆心坐标；(x0,y0)为轴承的内圆圆心坐标。

检测精度结果如表1所示，轴承尺寸检测系统在像素上的精度可以达到0.5个像素，轴承内外径测量误差在0.015 mm范围内，且检测系统的稳定性较好。

表1 轴承尺寸测量结果

时间复杂度是验证算法效率的重要标准，时间复杂度的高低会严重影响算法的运行效率。在轴承内外径尺寸检测的过程中，通过chrono函数得到最小二乘圆检测法，Hough圆检测法及本文方法的运行时间。具体时间如表2所示。

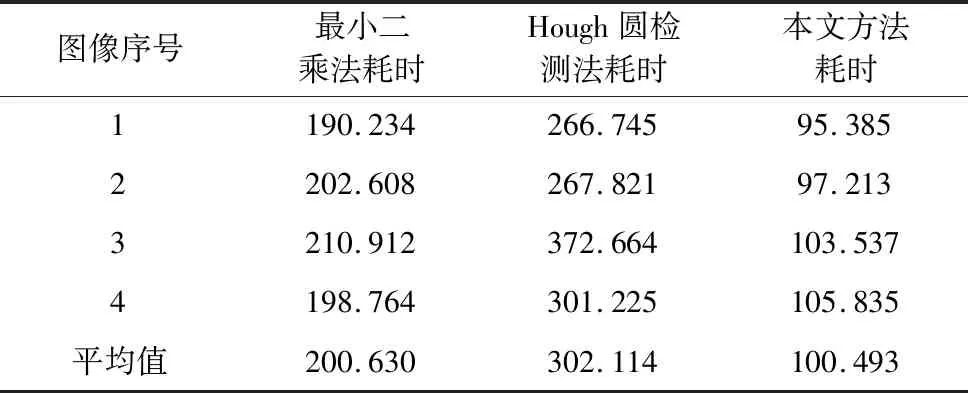
表2 时间复杂度对比 (ms)

通过表2 的对比结果可以看出，基于g2o(图优化)的尺寸检测优化方法在时间复杂度上远低于其他两种方法。这是因为g2o中不仅使用大量的类模板来提高运行效率，还使用了 Eigen 线性代数库来达到较高的计算性能，从而降低了时间复杂度。

5 总结

本文的重点是基于g2o(图优化)的尺寸检测优化方法的研究。以图像滤波处理、形态学操作、阈值分割为基础，消除了图像中的无关信息，增强了有关信息的可检测性；采用亚像素边缘检测获取亚像素边缘坐标，提高了轴承尺寸检测的精度；通过最小二乘法拟合初始曲线为迭代算法提供初始值，提高了迭代算法的稳定性；使用鲁棒性代价函数处理异常数据，并对优化结果影响较大的异常数据进行二次处理，减小了异常数据对优化结果的影响；把处理后的数据导入g2o中进行优化，从而得到圆心坐标和半径尺寸，提高了运行效率，降低了系统的时间复杂度。

实验表明，基于g2o(图优化)的尺寸检测优化方法达到了工业级的精度要求且算法的时间复杂度优于其他常规方法，为其它圆形零件的尺寸检测提供参考。