基于GA优化RBF网络的永磁同步电机无位置控制*

金 昊，丁曙光

(合肥工业大学机械工程学院，合肥 230009)

0 引言

永磁同步电机具有高功率密度和高效率的特点[1]，在电动汽车、数控机床等领域中发挥着越来越重要的作用。传统的永磁同步电机从安装在转子轴上的传感器来获得转子位置信息，但安装传感器增加了系统成本，降低了系统可靠性。因此，永磁同步电机无位置控制方法[2]被提出。

当前，无位置控制方法主要有：①基于模型参考自适应方法[3-4]，该方法实现简单，响应速度快，但对电机参数的依赖性高; ②高频信号注入估算方法[5-6]，该方法利用电机凸极效应，通过注入高频信号进行转子位置估计，受参数影响小，但需要外加励磁信号，并且只适用于低速无传感器控制; ③滑模观测器法[7]，该方法对外界参数扰动不敏感，响应速度快，鲁棒性强。但系统在低速运行时会抖动，影响系统稳态精度。随着神经网络理论的发展，许多和神经网络相结合的无位置控制方法被提出[8-10]。这类方法不依赖于精确的电机模型，对电机参数变化有较高的鲁棒性，扩展了可应用速度范围。

神经网络主要有反向传播(back propagation，BP)神经网络[11]和径向基函数(radial basis function, RBF)神经网络[12]。它们都是非线性多层前向网络，其中RBF比BP神经网络拥有更好的泛化能力，更高的精度及更快的收敛速度，能够逼近任意非线性函数。RBF神经网络算法是以梯度下降法[13]为基础的网络参数寻优,随机选取初始参数易使网络陷入局部最优，影响神经网络的收敛性。遗传算法是一种全局优化算法，通过GA优化RBF神经网络的初始参数[14]，能够有效避免搜索过程中易陷入局部最优问题。

为实现对SPMSM的无位置高性能控制，本文提出了GA-RBF算法，并与锁相环(phase-locked loop，PLL)技术一起应用于永磁同步电机无位置控制方法中，仿真实验结果验证了本文理论及控制研究的正确性和有效性。

1 永磁同步电机矢量控制模型

两相静止坐标系下的表贴式永磁同步电机数学模型为：

(1)

其中，uα、uβ为两相静止坐标系下α和β的定子电压；iα、iβ为两相静止坐标系下和的定子电流；Rs为定子电阻；Ls为电感；ψf为永磁体磁链；ωr为转子电角速度；θe为转子位置角。

将式(1)变形可得：

(2)

(3)

其中，Eα和Eβ为两相静止坐标系下反电动势。

电机运动方程为：

(4)

其中，J为转动惯量；Pn为极对数；iq为轴电流；TL为负载转矩；B为粘性摩擦系数。

2 GA优化的RBF神经网络观测器

2.1 RBF神经网络

RBF神经网络结构如图1所示。

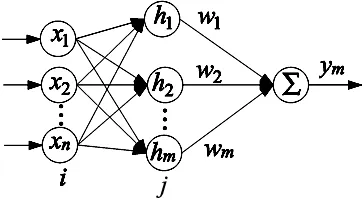
图1 RBF神经网络

图1中隐含层的输出由高斯函数构成：

(5)

(6)

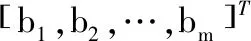
(7)

RBF 网络输出为：

ym(t)=w1h1+w2h2++wmhm

(8)

权值向量为:

(9)

采用梯度下降法对神经网络的训练过程如下：

(10)

wj(t)=wj(t-1)+Δwj(t)+α(wj(t-1)-wj(t-2))

(11)

(12)

bj(t)=bj(t-1)+Δbj+α(bj(t-1)-bj(t-2))

(13)

(14)

cji(t)=cji(t-1)+Δcji+α(cji(t-1)-cji(t-2))

(15)

其中，η∈(0,1)为学习速率；α∈(0,1)为动量因子；y为理想输出；ym为神经网络输出。

2.2 GA优化的RBF神经网络

遗传算法是一种自然选择的过程，它借鉴生物进化理论，把问题模拟成一个生物进化过程，通过遗传、交叉、变异、选择等操作产生下一代的解，并逐步淘汰适应度函数值低的解，保留适应度高的精英个体。

而RBF神经网络RBF神经网络采用梯度下降法训练参数时，对初始参数值敏感，初始参数选取不当可能会让神经网络陷入局部最优。所以利用遗传算法对神经网络中的初始参数进行优化，这样可以提高RBF函数的性能。

采用遗传算法优化RBF神经网络的步骤如下：

(1)初始化参数：种群规模，最大遗传代数，个体基因长度，交叉概率。对基因进行编码,随机产生初始种群。本文采用直观且运算量较少的实数编码方式对RBF函数中心、基宽进行编码操作。

(2) 计算每个个体的评价函数，分配适应度后将其排序，可以按照下式概率值选择网络个体：

(16)

其中，fi为个体的适应度值，可用误差平方和来衡量，即:

f(i)=1/E(i)

(17)

(18)

其中，N为种群大小；L为样本数;T为仿真时间。

采用轮盘赌的策略选择出适应度高的基因后，保留精英个体。

(3) 以交叉概率对种群中的个体进行交叉操作，重组种群后再以变异概率对种群中的个体进行变异操作，将新个体插入种群之后计算子代的适应度函数值。记录每代的最优解。

(4) 返回(2)循环操作，直到最大遗传代数时结束。比较每一代的最优解，计算最小误差，得到最佳个体。

2.3 观测器设计

如图2所示为神经网络观测器框图。

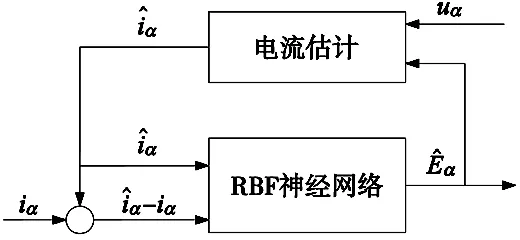
图2 RBF神经网络观测器

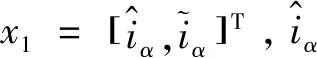
本文算法是利用遗传算法对RBF函数中的基宽数b以及中心向量c一同进行优化，然后RBF神经网络观测器采用优化后的参数对反电动势进行在线估计，其中RBF函数中心、基宽、输出权值采用梯度下降法进行训练，经历多个误差修正学习过程，实时调整。

2.4 锁相环转速估计

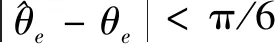
(19)

通过调节PI参数即可得出估计角度和转速，如图3所示。

图3 PLL原理框图

3 仿真结果与分析

为了验证两相静止坐标系下RBF神经网络观测器对表贴式永磁同步电机( surface permanent magnet synchronous motor, SPMSM)的观测效果，本文进行了仿真试验。电机仿真参数见表1所列。

表1 电机仿真参数

基于RBF神经网络的永磁同步电机模型参考自适应控制系统如图4所示。仿真的环境是软件Matlab/Simulink。

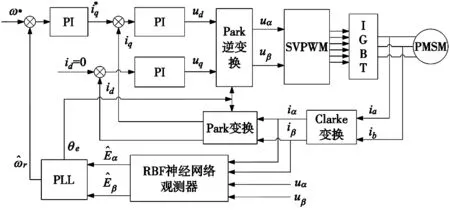
图4 SPMSM无位置矢量控制

为验证所设计的RBF网络控制器应用于永磁同步电机调速系统的动、静态性能表现，在下列条件下进行仿真测试：

(1)系统空载运行且给定转速为2000 r/min；

(2)待系统进入稳态后在t=0.2 s时突加负载为2 N·m。

遗传算法的初始参数：种群规模N=40；最大遗传代数MAXGEN=50；个体长度PRECI=10;代沟GGAP=0.95;交叉概率px=0.7；变异概率pm=0.01；因为对2-9-1的神经网络结构的基宽和中心向量进行优化，所以待优化的变量个数为n=9+2×9=27。

系统运行过程如图5所示。误差进化曲线如图6所示。

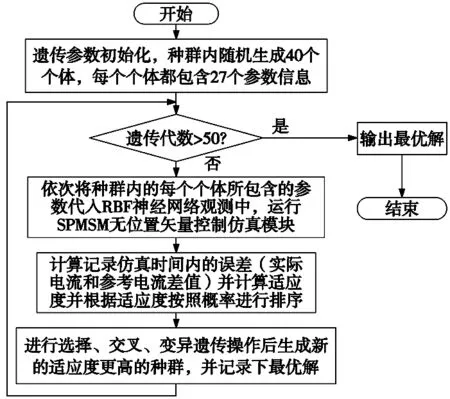
图5 GA-RBF神经网络算法流程图

图6 误差进化曲线

如图7所示为RBF神经网络采用随机初始值和采用遗传算法优化初始值的输出误差对比图。

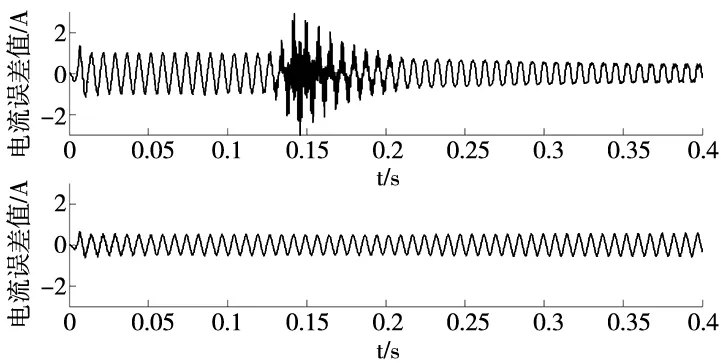
图7 电流误差值对比图

从图7可以看出采用随机初始值的RBF神经网络在开始阶段收敛效果较差，并且在中段出现波动，收敛不稳定；而经遗传算法优化后的神经网络误差较小，稳定性高，收敛性好。

图8是设定电机转速为2000 r/min时电机实际转速与估计转速波形图。从图中可以看出，电机于0.04 s左右稳定在设定转速，稳态误差0.25%左右。0.2 s突加负载后，转速产生下降30 r/min,动态响应时间约为0.02 s，于0.22 s时恢复稳态。

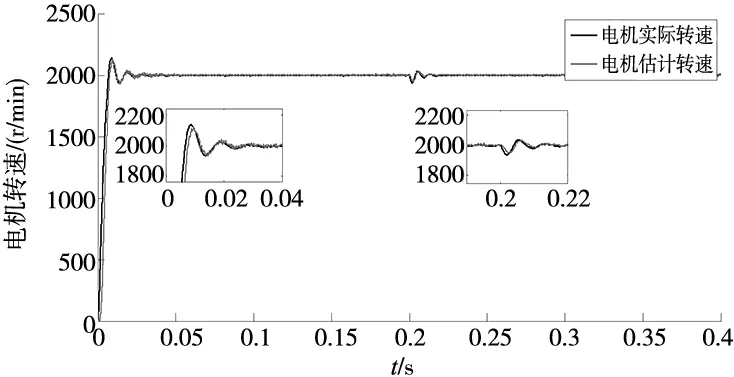
图8 电机转速实际值与估计值对比图

4 结论

本文将GA和RBF神经网络相融合的优化算法，提出了GA-RBF神经网络算法，大大改善了RBF神经网络的收敛性。利用GA-RBF来估计PMSM的反电动势，结合PLL技术估计转子位置及转速。仿真实验结果表明，整个系统具有良好的动态响应能力和一定的抗干扰能力，从而实现了电机的无位置高精度控制。