数控机床在机检测中触发式测头误差变速补偿*

白 克，黎 智，吴立辉

(1. 河南经贸职业学院，郑州 450000; 2. 四川省装备制造业机器人应用技术工程实验室，四川 德阳 618000; 3. 河南工业大学机电工程学院，郑州 450052)

0 引言

触发式测头测量系统在数控机床上的应用较为广泛[1-4]，但测头的触发半径变化通常大于10 μm，这是造成在机测量误差的重要原因，直接影响加工精度。为了提高测量精度，可以采用各种有效的方法[5]。其中，最明显的一种方法就是为机床配备更加精确的测头，例如非接触式应变仪。但是，高精密的测头价格比较昂贵。

由于测头误差产生的主要原因是系统误差，因此提高机床测量精度的另一种方法是对测头的系统误差进行数字误差校正。该方法已成功地应用于坐标测量机(coordinate measuring machines，CMM)专用测头[6]，并且可以同样有效地应用于数控机床的触发式测头[7]。例如，Jankowski M等[8]对数控机床测头误差的力学模型进行了研究，验证了数值校正方法的可行性，并证实其精度受系统误差的影响要比随机误差的影响大。崔星星等[9]对测头预行程误差进行了统计学相关分析，并提出采用神经网络进行建模预测，分析结果也验证了数字误差校正的有效性。

但是，现有解决方案大多需要将错误数据上传到机床控制器并由其执行计算。如果沿机床的单轴进行测量，则计算很简单：只需将X、Y和Z坐标读数加上或减去已知的系统误差值即可。但是，若不沿单个轴进行测量时，由于必须分别在2或3个轴上进行校正，因此需要将每个测量方向上的3个误差校正值(每个坐标一个)上传到机床控制器，并使用三角函数进行计算来完成测量，导致计算会变得更加复杂。这意味着校正的效果在很大程度上取决于控制器的硬件和软件，导致在机检测系统误差补偿困难。

为克服该缺点，提出了一种新的测头系统误差变速补偿方法。该方法的优点是，可以在进行在机测量之前，离线进行所有计算的新速度值。无需单独计算三个校正值(X、Y和Z)。所提出的方法易于应用，可以轻松完成触发式测头在机测量，但其精度得到显著提高，误差可以降低10倍。

1 系统误差建模

测头的系统误差可以用触发半径特性和变化值来描述。触发半径的定义如下[10]：在方向i上进行测量时，如果TGi表示探针尖端的位置，并且Os表示最佳拟合元素的中心(为各个方向的触发点TG确定的)，则ri表示测量方向i上的触发半径，等于点Os和TGi之间的距离。触发半径变化量Vr表示测头触发半径最大值和最小值之间的差。

触发半径变化与测球的形状偏差相对应，因此可以利用它对测头的实际性能进行很好地说明。然而，若使用另一个参数-预行程w，可以更方便地对测头进行理论建模。该参数的定义方法为：如果探针尖端的中间位置由N表示，则用wi表示的方向i上的预行程，等于点N和TGi之间的距离。相对于测头主体的中间位置N，每次测量所得的值可能会因测头滞后等原因而有所不同。但是，通常假定它是常数，即假定其变化可以忽略不计。这两个参数的图形说明如图1所示。

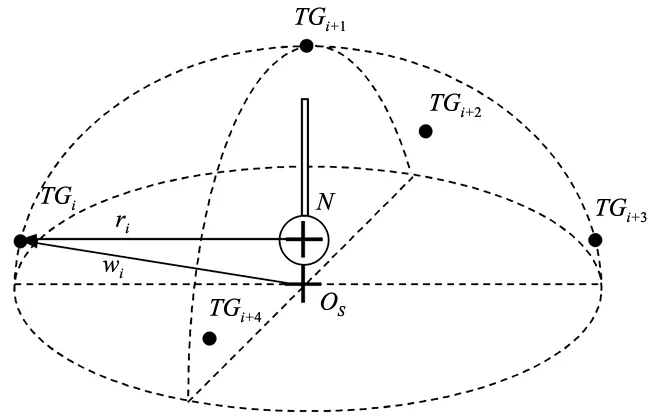
图1 测头触发半径和预行程的图形解释

假定点Os和N位于同一位置，则ri=wi。在实践中很少满足这一假设所需的条件，但是如果上述各点之间的距离足够小，则可以假设为ri≈wi。为了完成本文的研究，进行了这一假设。

方向i可以由两个角度α和β的值定义。α是方向i在垂直于测头轴线的平面上的投影与该平面上所选定线之间的夹角，而β是方向i与垂直于测头轴线的平面上之间的夹角。

先前的研究表明，在给定方向上的预行程与测量速度成正比：

w(α,β)=wT(α,β)+wI(α,β)=wT(α,β)+v(α,β)τ

(1)

式中，wT为与测头换能器相关的预行程分量，wI为与测量速度相关的预行程分量，v为测量速度，τ为换能器触发与测头控制器输出更改之间的延迟。

如果所有测量方向上的测量速度都相同，则所有测量方向上与测量速度相关的预行程分量也相等，如图2所示。

(a) 侧面示意 (b) 顶部示意图2 实现恒定的测量速度所需的测头预行程和总预行程

因此，有效探测半径(探针尖端半径减去预行程，即为了获得工件表面上测量点的坐标而必须移动所测机床位置的距离)在不同方向上是不同的，而机床刀具控制器通常仅使用有效探测半径的一个值。

所提出的测头误差补偿方法就基于编程可变测量速度的，所以与测量速度相关的预行程分量也是可变的，但总预行程在每个方向上都是相等的。探测误差仅受测头随机误差的影响。

2 误差变速补偿方法

为了补偿与测头换能器相关的测头预行程分量，与测量速度相关的预行程分量必须随着与换能器有关的预行程分量的增加而减小，公式如下所示：

(2)

(a) 侧面示意 (b) 顶部示意图3 应用变速误差补偿方法后测头的预行程和总预行程

为了达到这个目的，应按下式对测量速度值进行计算：

(3)

如上所述，预行程是适用于测头行为建模的参数，但是在实践中，触发半径更为重要。因此，可能需要用触发半径值替换公式(3)中的预行程值。在这种情况下，测头误差映射和测量速度值计算的一次迭代可能会不够。在这样的情况下，则应该多次执行速度测定，每次都使用之前计算的测量速度值v1作为v0值。

3 实验结果与分析

分两步对该方法进行了具体验证：首先验证其在实验室中是否可以减小触发半径变化；然后验证其真实在机测量环境中是否具有适用性。

3.1 实验室测试

确定测头误差的最常用方法是在机床上对主工件进行测量[10]。在第一步中，通过使用测试装置对提出的方法进行了实验验证。该装置的方案如图4所示。该装置机械部分的照片如图5所示。

1.测试测头 2.探针尖端 3.主工件4.三轴向压电工作台 1.测试测头 2.探针尖端 3.主工件4.三轴向压电工作台

固定测试测头1，使其测头尖端2位于主工件3的中心，主工件位于3轴压电工作台4上，其位置由控制单元设定。为了测试测头在给定方向上的触发半径，主工件会通过压电工作台在该方向上移动，并读取与测头触发点相对应的坐标。确定触发半径变化量的触发半径变化确定的扩展不确定度U(Vr)= 0.6 μm(当覆盖因子k=2时)。

为了对本文的误差补偿方法进行验证，将其应用于两个三维触发式测头：雷尼绍OMP40-2和雷尼绍OMP60。按照文献[10]中确定延迟的方法(根据平均触发半径测量获得各种测量速度，从而推导出τ)获得OMP40-2测头的延迟τ值为12.68 ms，OMP60测头的τ值为25.35 ms。两种测头的初始测量速度均设置为50 mm/min，并且两种测头均配有50 mm 长的探针。

在应用误差补偿方法之前，进行10次测量后确定OMP40-2的触发半径变化等于11.0 μm。β角不同时测头的触发半径特征如图6所示(所有显示值均为10次测量后所取的平均值)。

图6 误差补偿之前OMP40-2在不同β角下的触发半径特征

从图6可以看出，触发半径特征呈现为3瓣形的。在β角的值较小时这种形状较为显著：当β=0°时，触发半径变化值Vr=8.6μm，而当β=80°时触发半径变化值Vr=2.3μm。这些结果与关于触发式测头的现有认知一致。触发半径特征的3瓣形是造成触发半径变化的主要原因。

应用误差补偿方法后，测量速度从26.46 mm/min变为69.87 mm/min，并且进行10次测量后触发半径变化减小到1.0 μm，这是测头随机误差值。在不同β角时获得的触发半径特征如图7所示(所有给出的值均为10次测量后得到的平均值)。从图7可以看出，空间触发半径特征是准球形的。这意味着已经成功消除测头的系统误差。

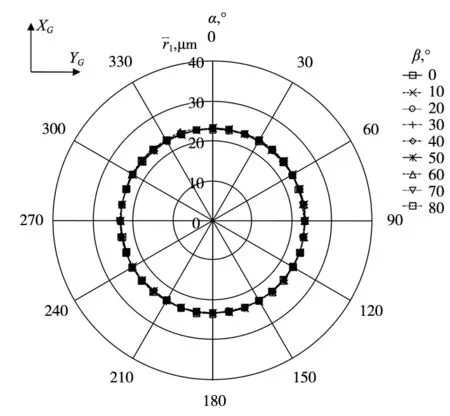
图7 误差补偿后OMP40-2在不同β角下的触发半径特征

当使用OMP60测头时，触发半径变化是在进行误差补偿之前进行10次测量得出的，等于16.8 μm。应用误差补偿之前在不同β角时获得的测头触发半径特征如图8所示(所有值均为10次测量后取得的平均值)。从图8可以看出，与OMP40-2测头的情况相同，触发半径是3瓣形的，这是三维触发式测头的典型特征。

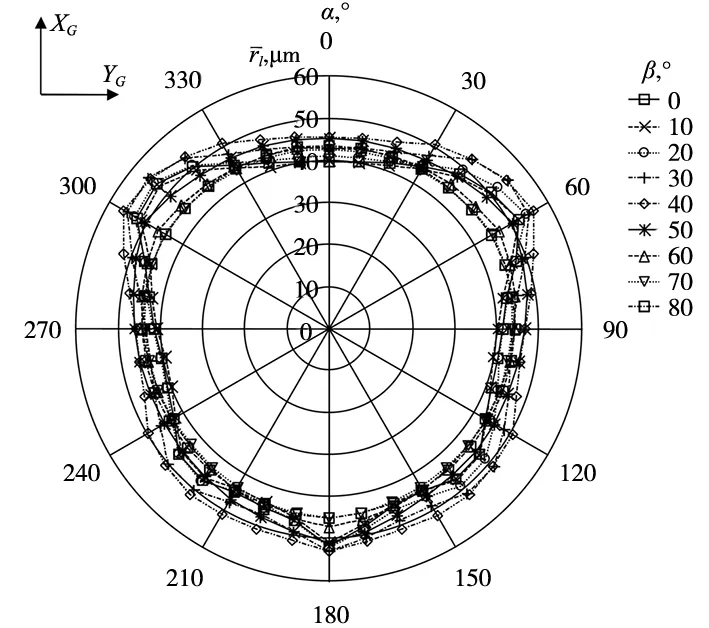
图8 误差补偿前OMP60在不同β角下的触发半径特征

应用所提出的误差补偿方法后，该形状会消失。测量速度从31.24 mm/min变化到66.18 mm/min，10次测量后确定的触发半径变化降至1.0 μm。不同β角的改进后准圆形触发半径特征如图9所示(所有值为10次测量后得到的平均值)。从图9可以看出，与OMP40-2测头的情况一样，系统误差得到消除。

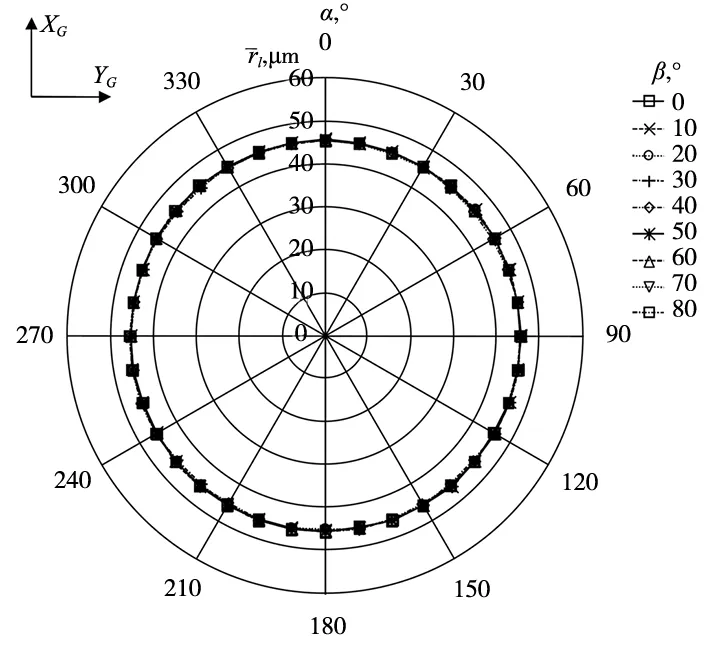
图9 误差补偿后OMP60在不同β角下的触发半径特征

3.2 数控机床在机检测

在实验室装置上进行的测试结果，证实所提出的方法能够将测头的系统误差降低10倍以上。为了验证采用本文方法后，是否会减少在机检测触发式测头系统(包括测头和机床)的误差，对测球进行了在机测量。第三个测头是OMP40-2(非实验室测试中使用的OMP40-2)，配有100 mm长的探针，并且使用了Haas VF7数控机床。

为了确定该测头的延迟，对标称为52 mm的规环进行了15次在机测量：分别以50 mm/min的恒定速度进行5次测量，以100 mm/min的恒定速度进行5次测量，以150 mm/min的恒定速度进行5次测量。每次在36个点对环进行测量。按照文献[10]中确定延迟的方法，通过所获得的数据可计算出延迟时间τ=14.5ms。

为了确定所用测头的系统误差，以100 mm/min的恒定速度对测球进行了10次测量，每次测量109个点。所获得的形状偏差等于测头的系统误差，如图10所示(显示的值是10次测量所获得的平均值)。

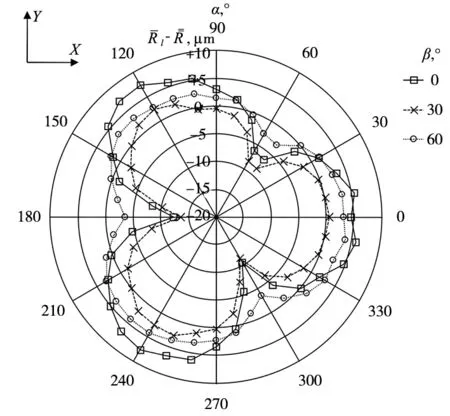
图10 不同的β角下所测球的测量形状偏差 (等于机床上所用OMP40-2的系统误差)

假设测球的形状误差可以忽略不计，考虑到10次测量所获得的平均值，则在Haas VF7数控机床上所得的探测误差的系统分量等于21 μm处测量的形状误差。由于随机误差的原因，单次测量中的形状误差会更大，获得的最大值为23 μm。

完成上述测量后，计算出一组新的测量速度值(最小值为43.594 mm/min，最大值为131.277 mm/min)，并使用这些新的速度值进行了10次测量。所获得的结果如图11所示(显示的值是10次测量后所得的平均值，等于机床上所使用OMP40-2的系统误差)。

图11 误差补偿后不同β角下所测球的测量形状偏差

从图11可以看出，根据10次测量所得到的数据，可知测得的形状偏差等于2 μm。单次测量获得的形状误差的最大值为6 μm。这表明，同样在机床上，所提出的方法可以将测头的系统误差减少到超出探头随机误差的水平。尽管需要执行多迭代的过程，但在实际测量环境中，该过程的第一次迭代就有效减小了系统误差。

为了确定测量时间是否显著增加，对相对增加时间ΔtR进行了计算(仅计算与测量速度有关的时间)，具体方法如下：

单个点处测量时间的速度相关分量ts等于：

(4)

式中，S为探针的接近距离，即从设置测量速度的点到被测量点之间的距离。

多点的测量时间tM是单点的测量时间之和：

(5)

式中，n为测量的次数。

为了确定由于应用误差补偿方法而导致的相对测量增加时间ΔtR，将应用方法之后的测量时间除以采用方法之前的测量时间，然后减去1：

(6)

根据该式可知，增加的测量时间主要取决于测量程序。在机床上进行109次测量后计算出的测量速度)，得出ΔtR=4.6%，可见应用方法之后的测量时间只是稍微有所延长。

4 结论

本文提出了一种新的测头误差补偿方法，避免了使用数控机床控制器进行复杂的计算。该方法通过设

置适当的测量速度，实现了测头误差的显著减小。对三维触发式测头进行的实验得出如下结论：①提出的误差变速补偿可以轻松完成触发式测头在机测量，且控制器无需进行任何运算，验证了其适用性；②在机测量精度得到显著提高，误差可以降低10倍，验证了提出方法的先进性。但是测量时间稍微有所延长，因此将在后续的研究中对此开展进一步研究。