柔性机械臂非线性干扰观测器的高阶滑模控制

周 晟，李 解，高 琳，史欣怡

(武警士官学校基层后勤管理系，杭州 310000)

0 引言

目前，机器人技术不断更新，为有效提高机器人工作效率，降低机器人工作时的能量损耗，将柔性连杆材料运用于机械臂的研制中[1]。对比于传统的刚性材料所制成的机器人，柔性材料及柔性结构具有低能耗、高负载、高响应、便于电机直接操作、等多项优点。对系统所构成的n个连杆所构成的机械臂系统，在重复考虑其柔性因素的条件下，通过设定2n个广义坐标完成对系统动态特性的研究，由此可知，柔性机械臂是一个刚柔耦合条件下的非线性系统，系统阶次变高对控制系统的设计产生极大的挑战。

在实际情况中，由于环境、资金、传感器安装等多种因素干扰，存在部分状态量难以获得，因此，为完成对柔性机械臂的操控任务，实现对机械臂的精准控制，将状态观测器引入系统[2]。文献[3]将具有主从结构的观测器引入系统，提高系统的工作准确性并且在一定情况具有控制器性能，完善整个系统的工作能力。文献[4]运用滑模控制方法降低柔性机械臂高非线性、高耦合和时变参量系统的控制难度，将滑模控制理论运用到相应控制模型中，提高整体控制的精准度。

在过去多数滑模控制系统的构造及观测中，其研究都基于一个限制条件，即设定系统的所有状态量为可观测状态，本文为提高控制精度降低对获取观测量的成本及传感器数目，将非线性观测器引入系统，考虑建模和测量的不确定性，负载变化及非线性摩擦阻尼干扰等多线影响，运用高阶滑模的控制方法，对系统进行准确测控，提高控的制整体准确性、稳定性。

1 模型建立

应用假设模态法(一种广义坐标近似法，采用有限个假设模态振动的线性和来近似描述弹性体振动)建立平面多连杆柔性机械臂动力学模型[5]。如图1所示。

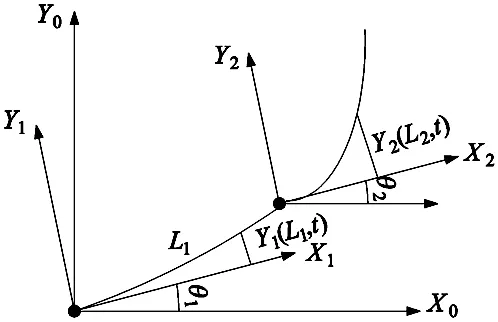
图1 柔性机械臂连杆示意图

柔性臂杆i的弹性挠曲度表达式如下：

(1)

其中，yi(xi,t)代表连杆i的弹性扰曲度，φij(xi)代表连杆i的第j个模态函数，Δij(xi)代表连杆i的第j个模态的广义弹性坐标(i=1,2,…n，j=1,2,…m)。

(2)

Δi(t)=[δi1,δi2,δi3…δim]

(3)

考虑连杆边界条件：

yi(0,t)=0yi′(0,t) = 0

(4)

平面多连杆柔性机械臂系统动力学方程表述构建[6]：

(5)

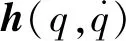
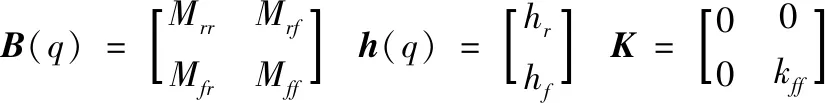
(6)

式中阻尼矩阵中的元素：

(7)

将式(6)代入式(5)可得：

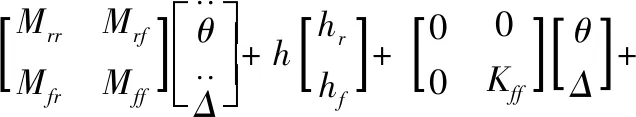
(8)

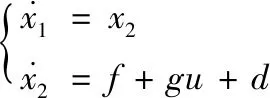
(9)

式中，d∈R2×1，设为参数不确定性及外部干扰数值综合，

(10)

(11)

假设2：双连杆柔性机械臂系统所受外部干扰及一阶导数有界。

(12)

正常数w，r分别为外部干扰和一阶导数的上界。

将式(8)变形可得：

(13)

定义状态变量如下：

(14)

得到平面多连杆柔性机械臂的状态空间：

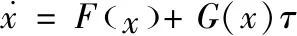
(15)

(16)

(17)

2 非线性状态观测器设计

定义如下变量：

ζ1=Δ，ζ2=Δ

(18)

将公式(5)改写为如下形式：

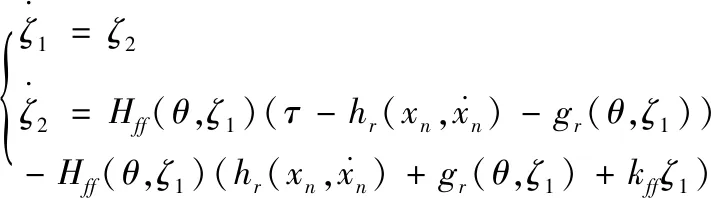
(19)

定义状态变量xn如下：

(20)

式(20)中，状态变量ζ1及ζ2为不可测参数，选取非线性观测器进行数值估计[7-8]。

引入非线性观测器将柔性机械臂动力学方程改写为如下形式：

(21)

(22)

定义非线性观测器观测误差ζe如下：

(23)

式(23)中：

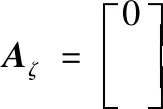
式中，矩阵Aζ为Hurwtiz矩阵，矩阵Bζ的模非常小。

3 控制器设计

由相应等式(5)可知，柔性机械臂系统自身耦合度高、非线性强的多输入多输成系统。文中依据图2所示，采用非线性干扰观测器同时运用高阶滑膜控制，降低系统整体振动情况，二者配合情况下降低干扰的影响，使得系统具有较强的鲁棒性[9-11]。

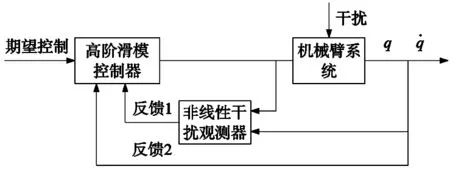
图2 控制系统框图

定义相应滑模面如下：

σ=x1-x1d

(24)

对式(24)滑模面求解二阶导数得：

(25)

为降低系统抖振提高机械臂运行准确性，对式(24)进行二阶求导得：

(26)

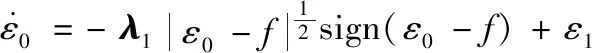
(27)

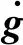
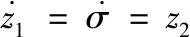
(28)

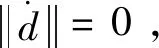
(29)

式中，w(t)∈R2×1，是待设计函数，其一般形式为：

(30)

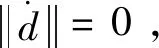
(31)

式中，j=2,3，α4=1，α3=α，α为介于0～1之间待设计的参数。

在实际系统中，外部干扰不可避免，因此需要设计补偿器对外界干扰进行相应补偿，增强系统的鲁棒性。对式(28)设计如下积分滑模面：

(32)

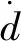
wd(t)=-βs-γsign(s)

(33)

式中，β=diag(b,b)为正定对角矩阵，

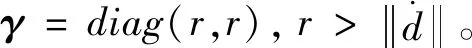
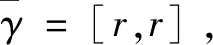
(34)

控制器作用下，有限时间内系统稳定。

求导得：

将式子代入得：

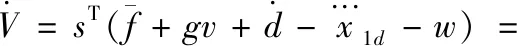
式中，ϑ>0，可知所示系统将在有限时间内稳定，实现控制作用。

4 数值仿真

设定柔性机械臂连杆基本参数：

m1=1 kg,m1=1.2 kg,L1=0.2 m,L2=0.3 m,
E1I1=10 N·m·rad-1,E1I1=5 N·m·rad-1,
J1=0.25 kg·m2,J2=0.025 kg·m2

所设计控制器给定参数如下：

λ1=diag(5.5,5.5)，
λ2=diag(2.5,2.5)，α=0.7，k1=0.5，
k2=1.5，k3=2，β=diag(0.5,0.5)，

λ=diag(0.05,0.05)

设定系统初始信号：x=(θ10,θ20)

设定系统期望信号：y=(15sin5t,10cos5t)

根据上述基本参数可得：

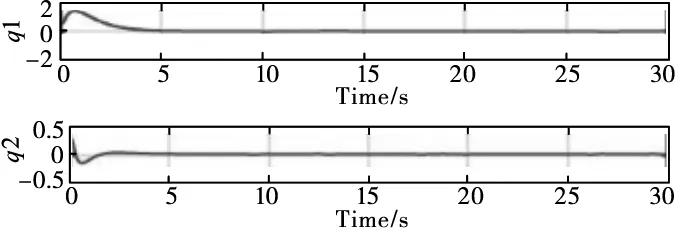
图3 假设模态信号

图4 控制器输出

由图4可知，初始时刻0 s～6 s时间段内，在干扰因素影响下，振动幅度较大，机械臂运动准确性、稳定性不高。在初始时刻6 s之后，控制器输出趋于平缓，机械臂运动趋于一致。采用非线性干扰观测器同时运用高阶滑膜控制，有效的削弱系统抖振，并且对外部干扰存在一定抑制，利于高精度工业生产，具有一定实际意义。

5 结论

本文构建多连杆柔性机械臂系统动力学模型，在控制系统中构建非线性干扰观测器，充分探究基于参数不确定性与外部负载干扰等因素产生的控制影响，基于高阶滑模控制器设计，赋予整个系统较优的抗干扰能力，展现对柔性机械臂的精准控制作业。分析系统的案例仿真验证了本次设计方法的准确性，对后续机械臂的控制研究奠定基础。