基于C-GRU的电机轴承故障诊断*
2021-03-01许爱华段玉波许瀚锋
许爱华,杜 洋,段玉波,许瀚锋
(1.东北石油大学电气信息工程学院,黑龙江 大庆 163318;2.国网山东省电力公司临邑县供电公司,山东 德州 251500)
0 引言
由于轴承在电机运行中的重要作用与地位,以及轴承故障诊断的复杂性,使电机轴承故障诊断成为了电机故障诊断研究领域的一个热点课题。之前的很长一段时间内对于轴承故障诊断工作的主流方案多是从为了有效的特征信息提取出发,通过采用各种有效的特征提取算法,对采集到的轴承振动信号进行多样的预处理,进而通过选择合适的分类模型对故障类型进行分类。受限于特征提取算法对于人工干预与专家经验介入的依赖,目前所使用的轴承故障分类方法的可靠性与准确性较低。
随着机器学习的进一步发展及深度学习的再次火热,目前部分学者开始将其与轴承故障诊断工作结合起来进行研究。郭亮等[1]通过提取时域、频域以及时频域特征输入到稀疏自编码网络进行训练分类;赵光权等[2]提出一种基于深度置信网络的故障特征提取及诊断方法;王丽华等[3]提出了一种基于短时傅里叶变换与卷积神经网络结合的电机故障诊断方法;袁建虎等[4]提出了一种基于小波分析基础上的时频图结合卷积神经网络的滚动轴承的故障诊断方法。上述几种方法的使用均在一定程度上提高了轴承故障诊断工作的效率和准确率,但同样摆脱不了对原始数据预处理工作的依赖。基于此,许爱华等[5]结合卷积神经网络处理大数据样本的优点,通过构建大数据样本,直接将原始数据作为卷积神经网络的输入,对模型训练分类,不再需要对数据进行预处理,较大程度上摆脱了人工干预和经验干预。该方法实现了一定的突破,但需要大量训练样本方能发挥其强大的自学习能力,在一定程度上降低了轴承故障诊断工作的效率。因此,本文结合卷积神经网络特征提取的优势和门控循环单元处理时序数据的有效性,提出了基于卷积神经网络与门控循环单元(C-GRU)的轴承故障诊断模型,使用Softmax分类器进行分类,希望在样本数量减小的情况下也能获得较好的准确率。
1 C-GRU轴承故障诊断模型
1.1 卷积神经网络特征提取过程
因本文后续用到卷积神经网络(CNN),故这里对CNN的特征提取过程做一个简单的介绍,CNN通过构建卷积层,对输入的数据进行卷积运算后生成新的数据,新数据的每个值即代表卷积核所覆盖的一小片区域内数据的一个特征表示。在模型的卷积层间,卷积核通过对提取的特征矢量进行卷积操作后,使用非线性激活函数构建新的特征矢量,同时,每个卷积层的输出结果均对应多对输入特征的卷积结果[6-8]。其数学表达式为:
(1)
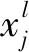
(2)
同时通过设置池化层,对每个覆盖区域中选择一个具有代表性的向量值,实现对特征向量的约简[10]。通过池化层的操作,能够大大减少数据的空间大小,并减少参数数目,提高模型的训练效率。此外,池化层的存在使得CNN网络对于噪声干扰具有一定程度的“免疫性”,即降低训练样本中噪声对池化层输出的影响。
1.2 GRU单元时序信息提取过程
GRU单元作为循环神经网络(RNN)的一种,和长短期记忆人工神经网络(LSTM)一样,他们的提出都是为了解决反向传播和长期记忆中的梯度消失或爆炸问题而提出的,GRU单元内部将LSTM内部中三个控制门的结构改为了两个控制门的结构,在提高了效率的同时,与LSTM具有相似的效果。
1.2.1 重置门与更新门
GRU单元将LSTM单元中的输入门、遗忘门以及输出门的结构,减少为重置门与更新门两个门的结构,从而改变了LSTM中对隐藏状态的计算方式。重置门的作用是有助于捕捉时序数据中短期的依赖关系,而更新门的作用是有助于捕捉时序数据中长期依赖关系。重置门与更新门的结构如图1所示。其中GRU单元中的重置门与更新门的输入均为当前时间步Xt,与上一时间步的隐藏状态Ht-1,输出的值由激活函数为Sigmoid函数的全连接层计算得到[11]。

图1 GRU单元中重置门与更新门的计算
具体来说,假设隐藏单元个数为h,给定时间步t的小批量输入Xt∈Rn×d(样本数为n,输入个数为d),和上一时间步隐藏状态Ht-1∈Rn×d。重置门与更新门的计算如下:
Rt=σ(XtWxr+Ht-1Whr+br)
(3)
Zt=σ(XtWxz+Ht-1Whz+bz)
(4)
其中,Wxr,Wxz∈Rd×h和Whr,Whz∈Rh×h是权重参数;br,bz∈R1×h表示差参数。由于Sigmoid函数可将元素的值变换到0和1之间。因此重置门Rt和更新门Zt中每个元素的值域都为[0,1]。
1.2.2 候选隐藏状态

(5)
在式(5)中,Wxh∈Rd×h和Whh∈Rh×h表示为权重参数,bh∈R1×h表示为偏差参数。从式(5)可看出,重置门的存在,决定了前一隐藏状态是否能够与当前候选隐藏状态控制相连接,而前一隐藏状态中可能保存了在其之前的历史时序信息,因此重置门可用以丢弃与预测无关的信息。

图2 GRU单元中候选隐藏状态的计算
1.2.3 隐藏状态
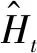
(6)
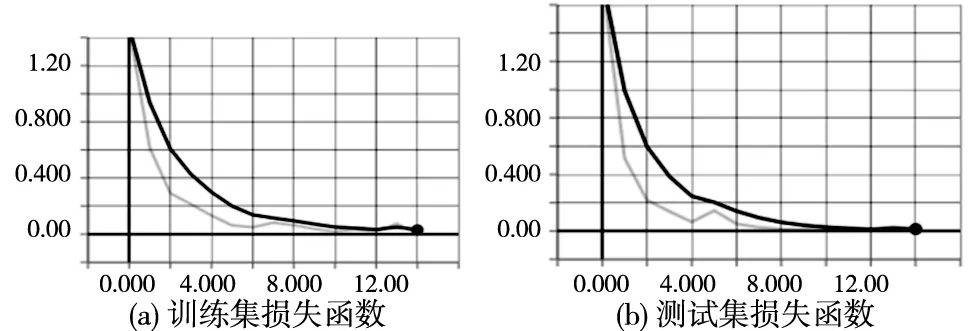
需要注意的是,更新门通过控制隐藏状态,决定着候选隐藏状态中所包含的是时序信息是否更新,如图3所示。假设更新门在时间步t′到t(t′ 图3 GRU单元中隐藏状态的计算 在本文中,由于所使用轴承故障数据为一维时序数据,因此在使用CNN网络进行特征提取时,需将卷积操作同样设置为一维。并且为了能够将CNN算法在数据特征提取的优点,以及GRU网络在处理时序数据的优点有效结合起来,本文中所使用的模型前端设置为CNN网络,后端设置为GRU单元。通过网络前端搭设的卷积层等结构实现对故障信息的特征提取后,进而通过GRU网络层实现对提取后的特征中所蕴含的时序信息深入挖掘后,最终使用Softmax分类器分类不同类型的电机轴承故障。 为了保证模型的训练效率以及分类的可靠性,在经过多次实验综合对比后,最终确定了本文所搭建的基于C-GRU的电机轴承故障诊断模型结构如图4所示。其中,第1、3、5、6层为卷积层,并分别将卷积核的数目设置为256、128、64、32个,卷积核尺寸设置为1×4,以实现对数据进行特征提取工作。此外,为了提高模型的鲁棒性以及保障模型能够学习到有效特征信息,本文所用的是从不同方向或位置采集到的同一故障类型的数据,因此将卷积层设置为多通道处理模式,以提高模型的训练和学习效率。同时,由于样本数量众多,故在模型训练过程中,模型极易出现过拟合现象,使得模型的训练效率大幅度下降,因此将第2、4、7层分别设置最大池化层,并将池化尺寸设置为1×2,以提取数据特征中的局部最大值,有效降低参数数量,在一定程度上降低过拟合的可能性。由于GRU模型训练过程中的单向性,多层结构的GRU会大大延长模型的训练时间,因此为了保证模型的训练效率,将第8、9层设置为GRU单元层。同时,由于GRU网络中单元的数量决定着对时序信息提取的效率,为了能够更好的提取电机轴承振动信号中所蕴含的时序信息,以及为了减少网络模型的复杂程度,将两层GRU单元层中的单元数分别设置为128个,实现在减少模型复杂度的同时,能够有效的提取出数据中所蕴含的时序特征。将最后3层设置为全连接层,将模型前端中网络结构所提取的大量的有效信息进行平铺处理,重新构成一维向量。将第3层全连接层设置为分类层,最终使用Softmax分类器分类不同类型的电机轴承故障。 图4 基于C-GRU的电机轴承故障诊断模型 实验采用的数据来自于美国凯斯西储大学开放轴承数据库,使用Tensorflow与Keras深度学习框架搭建卷积神经网络模型,将原始数据进行打标签后输入进行训练分类。所选样本数据采样频率为12 kHz,数据样本分别选取正常状态数据,0.007 in、0.014 in和0.021 in故障尺寸下的轴承内外圈及滚珠故障数据。这些数据样本按照3个不同点分别对应作为3个通道的输入数据,数据分别对应不同通道按组输入。 为了方便对比验证,本文首先搭建了基于CNN的轴承故障诊断模型,依据数据量的不同分别选用了两个数据集。数据集1中10个类型共1440万个样本数据分为4800组,数据集2中10个类型共720万个样本数据,数据量是数据集1的一半,具体的样本组成如表1、表2所示,训练和测试样本均是随机按照49:1的比例选取。 表1 数据集1样本组成 表2 数据集2样本组成 基于CNN的模型共10层,模型的第1、3、5、6层为卷积层,并分别将卷积核的数目设置为256、128、64、32个,卷积核尺寸设置为1×4,采用3通道处理方式。第2、4、7层为最大池化层,池化尺寸为1×2。并在模型的最后设置3层全连接层(其中最后一层为分类层),实现对轴承故障分类。 分别使用数据集1与数据集2对基于CNN的轴承故障诊断模型进行训练分类,并将模型的最大迭代次数设置为15次。使用Tensorflow中可视化工具Tensorboard将模型的训练结果可视化后,使用数据集1的训练与测试的准确率及损失函数值如图5、图6所示,使用数据集2的训练与测试的准确率及损失函数值如图7、图8所示。 图5 CNN模型使用数据集1训练与测试准确率 图6 CNN模型使用数据集1训练与测试损失函数 图7 CNN模型使用数据集2训练与测试准确率 图8 CNN模型使用数据集2训练与测试损失函数 由图5、图6所示,基于CNN的轴承故障诊断模型使用数据集1进行训练后,测试集中准确率与训练集中的准确率基本没有差别;对比损失函数值,测试集的普遍略小于训练集,证实了该参数设置下的CNN网络模型的分类准确性较高,较好地避免了过拟合或欠拟合的现象发生。而由图7、图8所示,使用数据集2进行训练后,CNN模型训练与测试的准确率虽达到了94%,但是训练与测试集的损失函数值较高,说明在使用数据集2进行训练的过程中,基于CNN的轴承故障诊断模型出现了严重的过拟合现象,严重影响了轴承故障诊断工作的可靠性与准确性。 接着使用本文所搭建的C-GRU模型,直接使用数据量较少数据集2对搭建好的网络模型进行训练,同样将网络的最大迭代次数设置为15次。使用可视化工具Tensorboard将模型的训练结果可视化后,训练集与测试集的准确率和损失函数曲线如图9、图10所示。 图9 C-GRU模型使用数据集2训练与测试准确率 图10 C-GRU模型使用数据集2训练与测试损失函数 与基于CNN的轴承故障诊断模型相比,在训练样本减少一半的情况下,本文所搭建的C-GRU网络模型通过深入挖掘原始数据中所蕴含的时序信息,使得最终的训练与测试准确率与采用数据集1进行训练后的基于CNN的轴承故障诊断方法获得的结果基本相近,最终测试集的准确率为99.7%,且测试集的损失函数也低于训练集的损失函数,未出现过拟合的情况。 前一部分使用国际通用数据集进行测试验证了C-GRU模型的可行性,为了进一步验证该模型在实际电机轴承故障诊断分类中的应用情况,使用实验室QPZZ-II旋转机械振动分析及故障模拟实验系统平台进行电机轴承故障诊断测试。如图11所示,该试验台主要由0.75 kW变速驱动电机、变频器、平衡盘、齿轮箱以及轴系总成等组成。本次故障诊断测试中使用的轴承型号为N205,故障类型分别为外圈、内圈、滚珠以及混合故障,其中混合故障为外圈与滚珠故障组成。上位机采集软件使用Labview编写数据采集程序,数据采集卡使用NI PCI-6251加SCB-68A接线盒,加速度传感器使用的是兰德公司的BZ1151三轴加速度传感器,采集卡采样率设置为12 k,电机工频额定转速运行。 图11 QPZZ-II旋转机械振动分析及故障模拟实验系统平台 将采集到相同位置中x轴、y轴、z轴的数据作为3个通道,每个通道的每组数据量为1000按组输入至本文搭建的C-GRU轴承故障诊断模型进行训练和测试,样本数据组成如表3所示。 表3 QPZZ-II型平台电机轴承数据样本数据组成 由图12可以看出经过15次的模型迭代后,本文中所搭建的基于C-GRU的电机轴承故障诊断模型,在实验室QPZZ-II电机试验台轴承故障诊断工作中的训练准确率与测试准确率分别为99.1%和99.6%,与凯斯西储大学开放轴承数据库数据训练测试的准确率基本相同。同时在图13中,测试集损失函数略低于训练集损失函数,未出现过拟合的情况。由上述结果可看出,本文所搭建的网络模型在不同的电机轴承故障诊断中均具有较高的诊断效率与可靠性,达到了预期的训练和诊断效果。 图12 QPZZ-II电机平台轴承故障训练与测试准确率 图13 QPZZ-II电机平台轴承故障数据训练与测试损失函数 本文所提出的基于C-GRU轴承故障诊断模型取长补短,一方面结合了卷积神经网络(CNN)在处理大数据特征提取中的优势和门控循环单元(GRU)善于处理时序数据的特点,另一方面也在一定程度上弥补了单一CNN和GRU各自的不足。通过多次实验选择合适的模型结构,将前端CNN网络对电机轴承故障数据进行特征提取的数据作为后端GRU网络的输入,充分挖掘了电机轴承故障数据中所蕴含的时序信息。通过使用凯斯西储大学开放轴承数据库数据,以及实验室QPZZ-II型电机平台的数据对文中所搭建的网络模型进行训练分类,发现该方法在减少了对样本量需求的同时,很好地保障了电机轴承故障诊断分类的准确率,同时对不同的类型电机轴承同样具有很好的分类准确性,证明了该模型具有较强的鲁棒性,对于时序数据的分析分类具有一定的实用价值。
1.3 模型搭建与参数选择

2 通用数据集实验分析



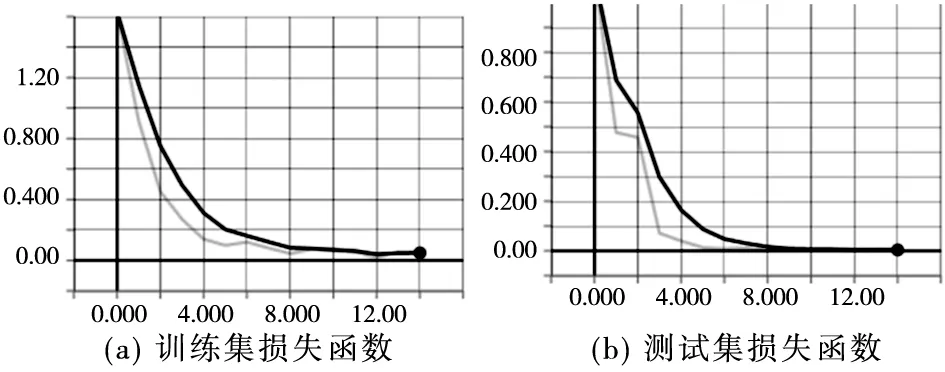

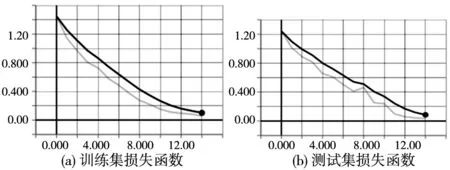


3 其他类型轴承故障分类对比实验分析



4 结论
