基于时频域改进型胶囊网络的轴承故障诊断*

孙 岩，彭高亮

(哈尔滨工业大学机电工程学院, 哈尔滨 150000)

0 引言

滚动轴承在各类机电一体化设备中使用广泛,由于工作环境恶劣、频率高等原因，轴承故障频发。时频分析是目前常用的轴承故障诊断方法之一，但受限于轴承工作环境噪声等因素，故障特征在振动信号中信噪比较低，直接进行故障诊断难度较大，常采用一些信号降噪、分解的方法辅助识别。传统信号处理方法过程繁琐，不能自动识别特征，依赖人员经验较多。随着人工智能技术的发展，越来越多的学者提出智能化诊断方法。Zhang Wei等[1]提出一种从一维时间信号直接提取特征的方法，利用大小不同的卷积核实现噪声滤波和特征提取；Shao Haidong等[2]提出了一种基于极限学习机的深度小波自动编码器，用于滚动轴承的智能故障诊断；李恒等[3]提出了基于短时傅里叶变换和卷积神经网络的故障诊断方法,实现了端到端的故障模式识别。上述方法都取得了一定的效果，但存在结构相对复杂，尤其卷积神经网络，参数较多，调整复杂，没有从信号特征出发，因此需大量样本训练优化参数。本文提出一种从信号时频分布特征角度提取信号的方法，根据时频域特征采用直线性感受野，利用胶囊网络空间位置敏感性进行故障分类。

1 基本原理

1.1 时频分析

时频分析从时间和频率二维的角度观测信号的本质特征，原始一维振动信号为信号、谐波及杂波的混合体，从单时域和频域直接分析，故障特征规律不明显。时频分析采用升维的方法，将一维升至二维空间，信号可分性得到提高，物理意义明显。

目前常用的时频分析方法有短时傅立叶变换、Wigner-Ville分布、连续小波变换、S变换等。短时傅立叶变换以傅里叶变换为核心的，应用方便[4]。采用固定窗截取时域信号进行频谱分析，时频聚集性良好，瞬时频率物理意义清晰。相对于连续小波变换等可变基函数的时频方法，更加简单实用。本文采用短时傅立叶变换的方法将原始信号转换为二维时频分布图。

短时傅立叶变换公式为：

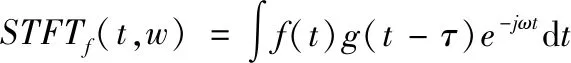
(1)

式中，f(t)、g(t-τ)分别为信号和窗函数。

滚动轴承内圈、外圈和滚动体故障信号特征频率计算公式分别如下：

(2)

(3)

(4)

式中，fi为内圈转频，D、d、α、z分别为截圆直径、滚珠直径、接触角和滚珠个数。

从轴承一般尺寸、应用场景(转速10 000 r/min以下)和以上公式可以得出，时频分析对低频段处理可覆盖全部故障特征频率。

1.2 LR-Capsulenet结构

1.2.1 胶囊网络

本文在传统胶囊网络[5]的基础上改进其特征提取层(卷积层)，更新为符合振动信号特征的直线性特征提取模块，减小参数量的同时，能够更准确的提取前端特征。基础胶囊网络主要思想为将一组神经元合并胶囊结构，其活动矢量代表特定类型的实体，使用活动矢量的长度来表示实体存在的概率，并使用其方向来表示实例化参数。其实现特定对象识别主要基于路由机制的构建，低层胶囊将其输出发送到更高层胶囊，通过向量的乘积大小得到低层与高层之间的相关性，从而使相关性强的低层高层之间建立联系，两层胶囊i和j之间路由过程如表1所示。

表1 动态路由算法表

通过上述过程可以看⑥过程中通过向量的乘积实现两层胶囊之间的关联性，低层向相关性强的高层输出；⑤过程通过压缩后向量长度判断特定对象存在性。

1.2.2 LR-Capsulenet

本文提出一种具有直线性感受野的新型胶囊网络结构，实现时频特征的重点提取和位置识别，从而达到故障类型分类。整体结构简单，参数较少，具体的网络如图1所示。

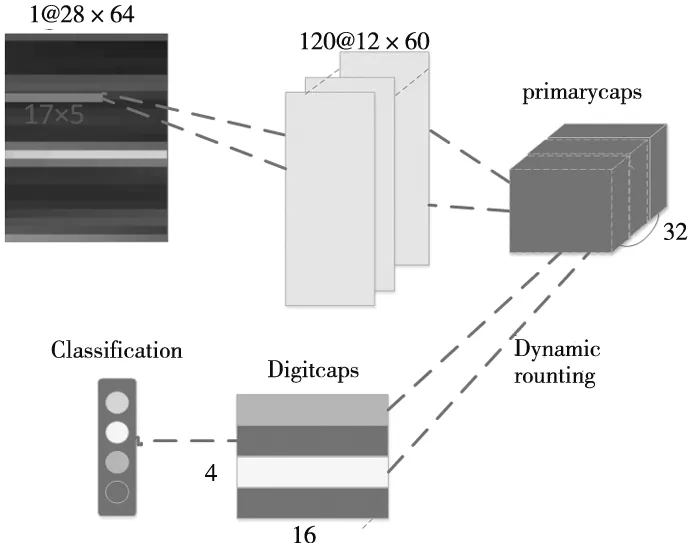
图1 LR-Capsulene结构

(1)输入图像尺寸

时频分析中，设定横坐标时间、纵坐标频率，频率具有聚集性特点，结构将输入层尺寸调整至28×64，加长频率轴，使频率谱线间距适当加大。图像设定为单通道图像。

(2) 卷积层

卷积层使用卷积核(ConvolutionalKernels)对输入信号(或特征)的局部区域进行卷积运算，并产生相应的特征[6]，卷积结果作为下一层的输入特征。结构中第一层采用卷积层提取图像特征，根据时频图中水平线物理意义上为特征频率，本文利用尺寸设定为17×5的120个长卷积核，提取低层特征，升维特征空间。长卷积核的优势在于体现时频图本质特征，节省卷积运算开支。

(3) 胶囊层

结构中采用主胶囊层(Primarycaps)和数字胶囊层(Digitcaps)。主胶囊层采用32个胶囊(神经元组)将低层信息分组，实现低层特征的组合。数字较曩层根据轴承正常、内圈故障、外圈故障和滚动体故障4类特征确定行数，通过路由机制主胶囊将特征相关性大的输出到数字胶囊，实现特征和空间位置的区分。

2 试验及结果分析

2.1 数据及预处理

本文轴承数据采用CWRU实验台数据，使用16通道DAT记录器采集振动信号。数据情况如表2所示。

表2 试验中使用的数据

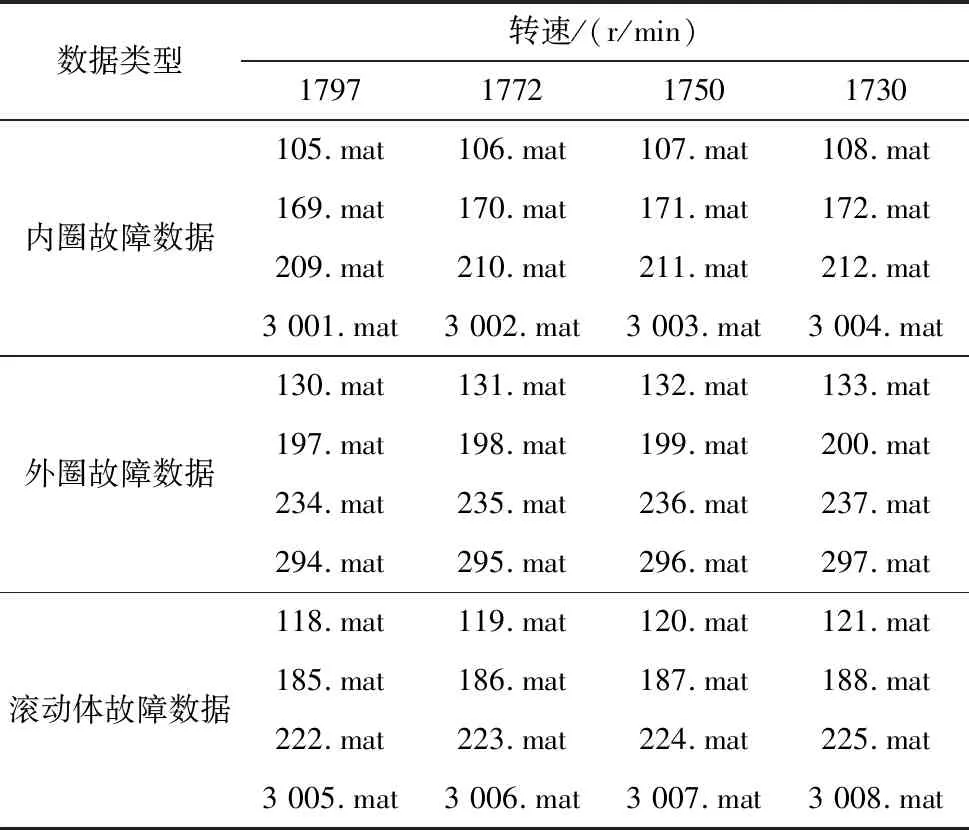
续表

试验中采用的所有数据文件中均有采样频率12 000 Hz的10 s或20 s左右数据，将每个数据文件内数据按3000个数据点间隔划分周期，取每个样本文件内所有整周期数据。

试验中使用轴承型号6205-2RS JEM SKF 深沟球轴承，轴承基本参数如表3所示。

表3 轴承参数表

根据轴承参数、转速和上文特征频率计算公式，可得全部特征频率在200 Hz以下。

每个样本经通带0～220 Hz的低通滤波器处理，短时傅立叶变换为时频图，图像处理为尺寸28×64的灰度图，总共是样本数为3560张时频图。正常、内圈故障、外圈故障、滚动体故障处理后的时频图如图2所示。

图2 4类时频图

从上图中可以看出，故障特征频率在时频图上呈现为直线形式；发生故障时，0～220 Hz时频图出现明显的变化，但三种故障类型通过直接观察无法区分。

2.2 实验验证和分析

将所有样本图片和对应标签按70%、30%比例随机划分为训练集和验证集。

为验证模型的优劣性，搭建具有传统结构的卷积神经网络，结构如图3所示。

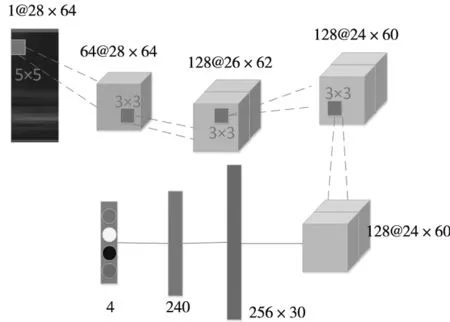
图3 卷积神经网络

图中卷积神经网络具有4个卷积层，3个全连接层，相比LR-Capsulenet层数和参数规模更多。

利用训练集训练卷积神经网络CNN和LR-Capsulenet，采用交叉熵损失函数和Adam优化[7]方法，结束后验证集对结果进行测试，训练及验证结果如图4、图5、图6所示。

图4 训练过程正确率

从训练过程正确率曲线可得，在相同的训练样本下LR-Capsulenet网络训练过程更稳定，最终训练达到的正确率更高。

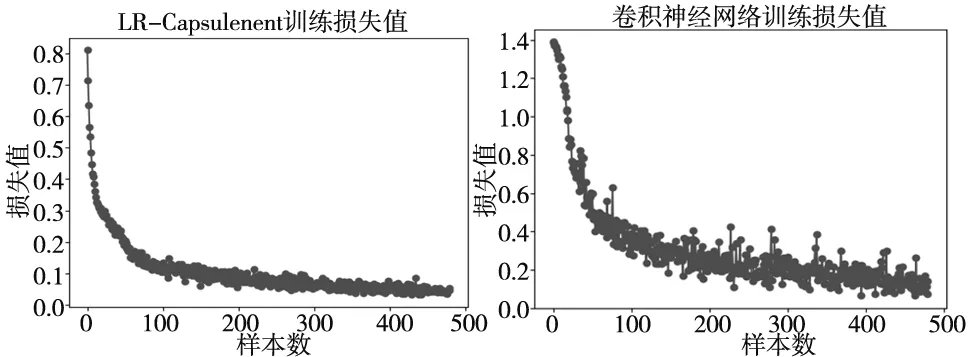
图5 训练过程损失率

损失曲线可得，在相同的训练样本下LR-Capsulenet网络交叉熵损失下降较快且更加稳定。

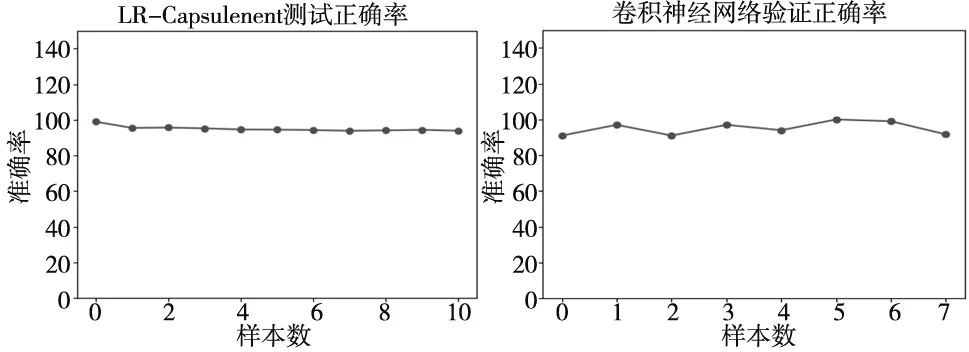
图6 验证集正确率

验证集正确率曲线可得，LR-Capsulenet网络正确率更高、稳定性更强，泛化能力更强。

综上结果本文提出的LR-Capsulenet在规模较小、参数少的情况下，能达到更好的时频图自动识别效果。

3 结论

轴承出现故障时，不同类型故障的振动信号时频分布具有不同特征，通过卷积神经网络等方式可以自动提取诊断出故障特征和类型，但存在网络规模较大等问题，需进一步改进优化，本文提出了一种利用信号时频特征规律的具有直线性感受野的新型胶囊网络，较少的层数和参数的网络结构达到了良好的效果。