聚环状对苯二甲酸丁二酯的非等温结晶动力学

周开河，白文博，朱艳伟，但扬清，颜 春，陈 刚*

（1.国网浙江省电力有限公司宁波供电公司，浙江 宁波 315010；2.宁波市电力设计院有限公司，浙江 宁波 315010；3.国网浙江省电力有限公司经济技术研究院，浙江 杭州 310007；4.浙江省机器人与智能制造装备技术重点实验室，中国科学院宁波材料技术与工程研究所，浙江 宁波 315201）

连续纤维增强热塑性复合材料具有高性能且可回收利用的特点，已成为复合材料领域研究的热点。环状对苯二甲酸丁二酯（CBT）是一种具有环状结构的单体或低聚物，其熔体黏度极低［1-2］，在锡类或钛类催化剂的作用下可以发生开环聚合生成线型热塑性聚环状对苯二甲酸丁二酯（pCBT）［3-4］。由于CBT的熔体黏度非常低，可以充分浸渍增强纤维或织物，因此，可以采用真空导入或树脂传递模塑成型等方法制备轻质高强的连续纤维增强热塑性pCBT基复合材料［5］。CBT开环聚合时无反应热放出，聚合温度约为190 ℃，低于pCBT的熔点，因此，CBT的开环聚合过程与生成的pCBT的结晶过程是同时发生的。半结晶性聚合物的力学性能和热性能与聚合物的结晶度及其晶态结构密切相关，因此，通过研究pCBT的结晶动力学，可获得相关的动力学参数，以及建立最终产品的加工工艺条件与其微观结构和性能之间的关系，为制备高性能的聚合物提供技术指导和理论依据。pCBT的相对分子质量对其结晶行为具有较大影响，对其进行非等温结晶动力学的研究目前还没有相关的报道。本工作研究不同相对分子质量pCBT的非等温结晶动力学，根据pCBT的结晶速率系数（CRC）和结晶速率参数（CRP）确定其非等温结晶速率，采用Avrami模型和Ziabicki模型分析pCBT的结晶动力学参数，通过Friedman微分等转化率法计算pCBT在非等温结晶过程中的有效能阻。

1 实验部分

1.1 主要原料

CBT，美国Cyclics公司，使用前于100 ℃真空干燥至少12 h。催化剂单丁基三异辛酸锡，纯度为98%，上海萨恩化学技术有限公司。

1.2 主要仪器

DSC214型差示扫描量热仪，德国Netzsch公司。

1.3 试样制备

在250 mL三口圆底烧瓶中加入100 g的CBT，在氮气保护下，采用油浴加热至190 ℃，待树脂完全融化呈透明状态后，将定量催化剂加入到树脂熔体中，机械搅拌使催化剂与树脂充分混合，反应1 h，即得到pCBT。采用质量分数分别为0.1%，0.2%，0.4%，0.6%催化剂制备的pCBT记作pCBTM1～pCBT-M4。

1.4 测试与表征

pCBT的特性黏度采用德国Schott公司的AVS 370型乌氏黏度计按GB/T 14190—2008测定。测试前pCBT于100 ℃真空干燥至少12 h，然后将定量pCBT溶解在苯酚与四氯乙烷（质量比3∶2）的混合溶剂中，配制成0.5 g/dL的溶液。特性黏度按式（1）计算。

式中：ηinh为特性黏度，dL/g；t为聚合物溶液的流动时间，min；t0为纯溶剂的流动时间，min；c为聚合物溶液的质量浓度，g/dL。

根据Mark-Houwink方程［6］，黏均分子量（Mv）按式（2）计算。

式中：K′和α为Mark-Houwink常数，K′=21.5×10-3mL/g，α=0.827［7］。

采用差示扫描量热法（DSC）研究pCBT的非等温结晶行为。氮气气氛，称取干燥试样5～8 mg，以20 ℃/min的降温速率（Φ）将试样从室温加热到250 ℃，保温5 min以消除热历史，然后分别以Φ为2.5，5.0，10.0，15.0，20.0，25.0，30.0，40.0 ℃/min降温。

2 结果与讨论

2.1 pCBT的非等温结晶行为

经计算，pCBT-M1～pCBT-M4的Mv分别为4 988，11 695，26 474，34 830。从图1可以看出：在136～204 ℃，所有pCBT的DSC曲线上均有一个尖锐的放热峰，且峰宽随Φ的增加而增加。其原因是由于随着Φ的增加，使聚合物链的重排时间逐渐减小，从而导致产生了小而不完全的晶体结构［8］。

从表1可以看出：随着Φ的增加，pCBT的初始结晶温度（θ0）、结晶速率最大时的温度（θmax）、半结晶温度（θ1/2）、半结晶时间（t1/2）均随之逐渐降低，此外，在相同的Φ下，θ0，θc和t1/2均随pCBT相对分子质量的增加而升高。

2.2 pCBT的非等温结晶动力学

基于非等温结晶放热曲线，在不同的Φ下，t时刻对应的相对结晶度（Xt）按式（3）计算［9-12］。

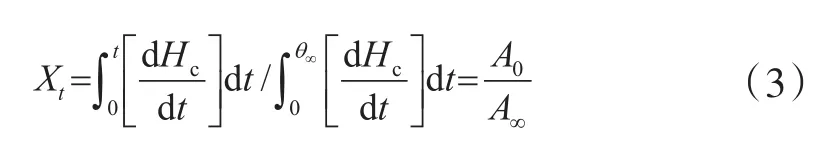
式中：θ∞为聚合物的终止结晶温度，℃；A0是温度从θ0到θ时DSC放热曲线的放热峰面积，J/g；A∞是温度从θ0到θ∞时DSC放热曲线的放热峰面积，J/g。

从图2可以看出：所有曲线均呈反S形，表明在结晶过程中Φ对树脂的结晶有热滞后效应，当Φ较低时，结晶发生在较高温度条件下，Φ越高，结晶发生的温度越低。

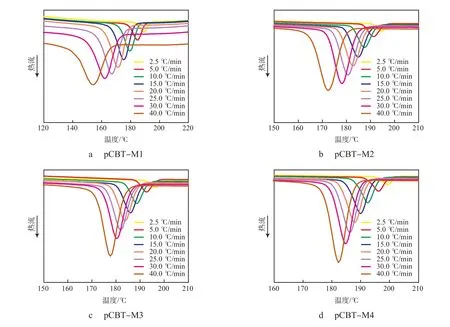
图1 pCBT的DSC结晶曲线Fig.1 DSC crystallization curves of pCBT resins

表1 pCBT的结晶参数Tab.1 Crystal parameters of pCBT resins

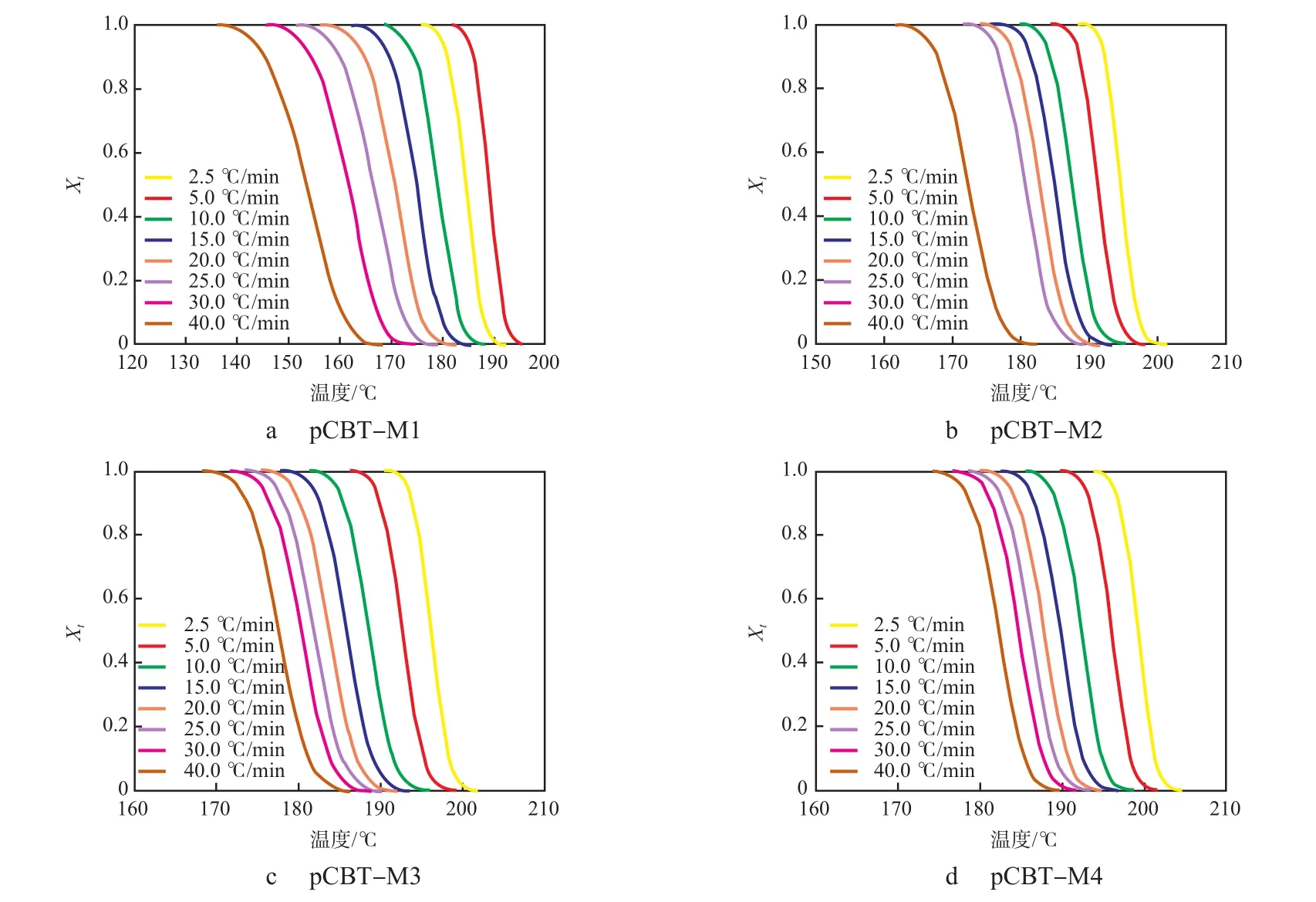
图2 pCBT的Xt随温度的变化曲线Fig.2 Relative crystallinity Xt of pCBT resins as a function of temperature

对于Φ恒定的非等温结晶过程，可按式（4）将图2中横坐标的温度转变为时间，从图3可以看出：随着Φ的增加，pCBT的总结晶时间减少。

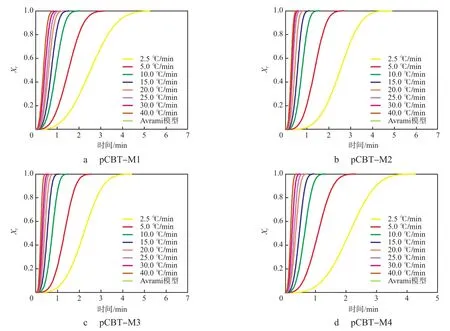
图3 pCBT的Xt随时间的变化曲线Fig.3 Relative crystallinity Xt of pCBT resins as a function of time

1/t1/2与pCBT的非等温结晶动力学参数如表2所示。1/t1/2越大表明结晶速率越快。从表2可以看出：1/t1/2随着Φ的增加而增加，表明pCBT的结晶速率随Φ的增加而增加。

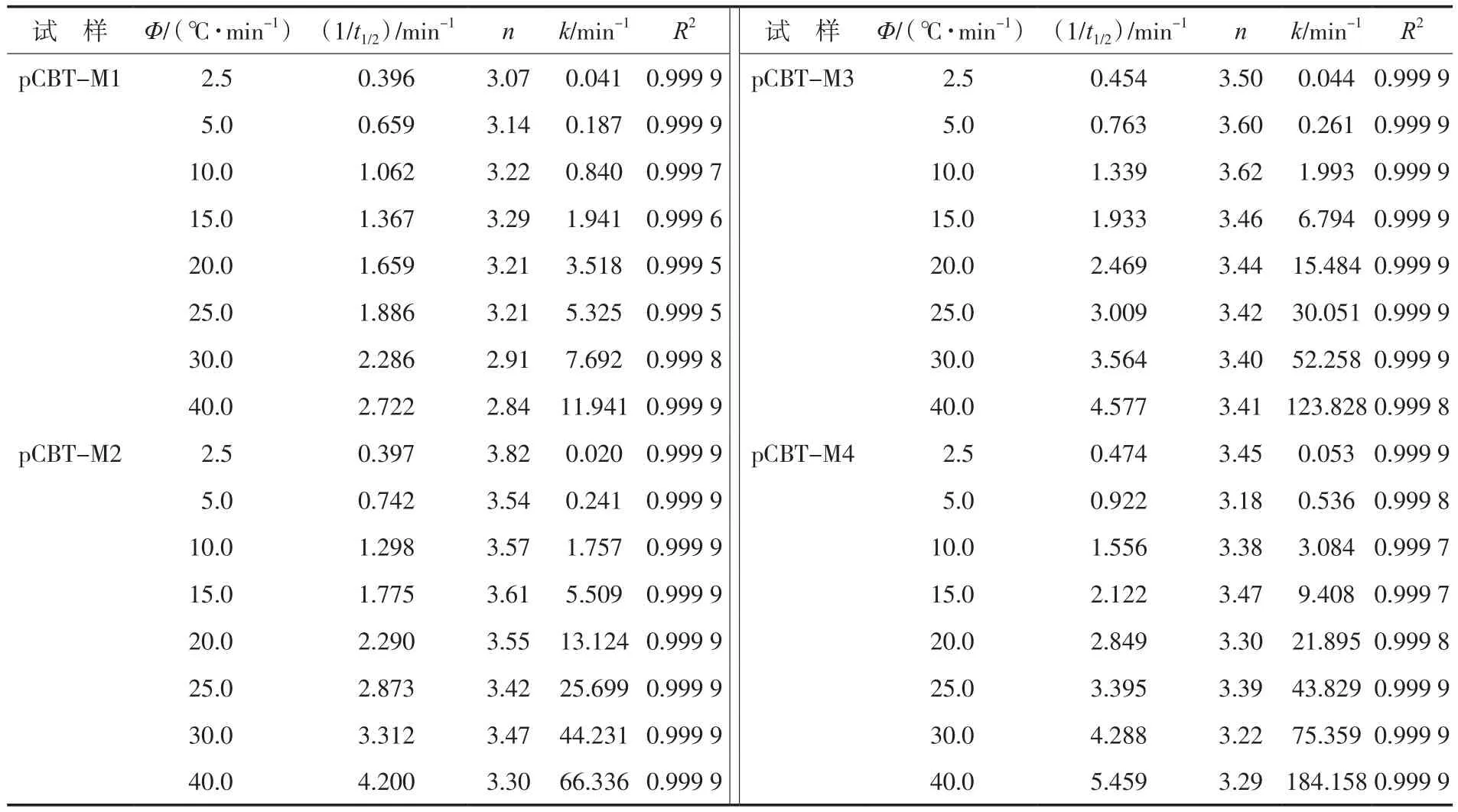
表2 pCBT的非等温结晶动力学参数Tab.2 Kinetic parameters of non-isothermal crystallization of pCBT resins

CRC［9-10］和CRP［9-11］可以用来判断非等温结晶速率。Φ与θmax呈线性关系，其斜率定义为CRC，见图4。1/t1/2与Φ呈线性关系，其斜率定义为CRP，见图5。

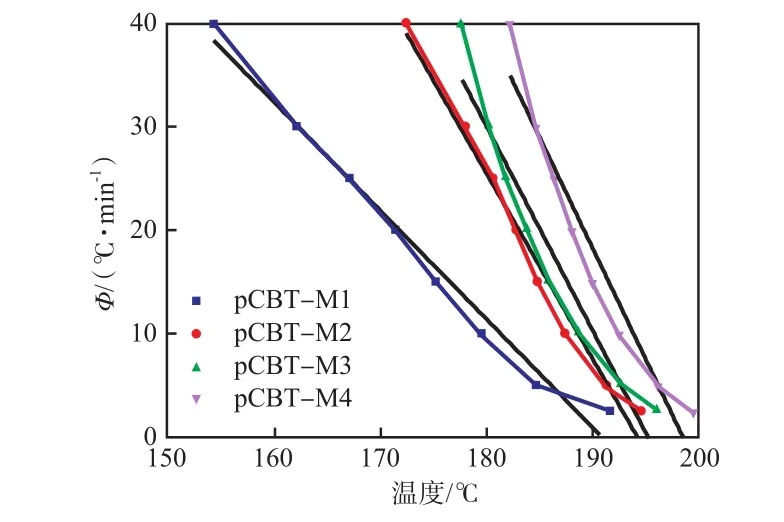
图4 pCBT的Φ与θmax的关系曲线Fig.4 Cooling rate Φ of pCBT resins as a function of θmax

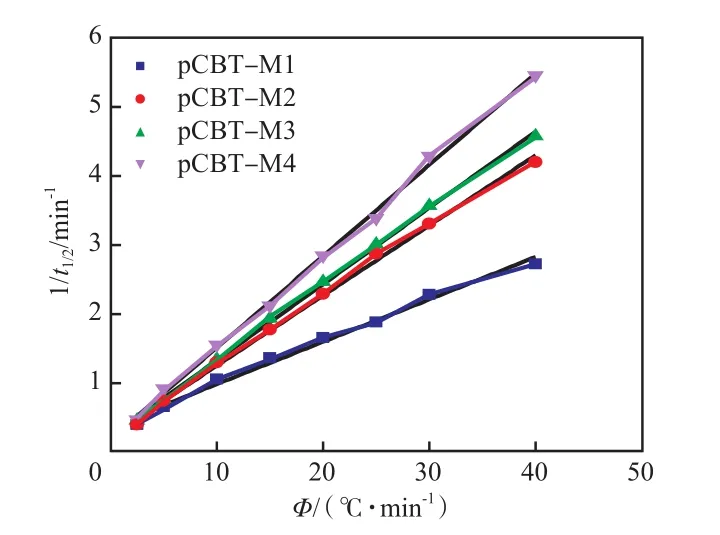
图5 pCBT的Φ与1/t1/2的关系曲线Fig.5 Cooling rate Φ of pCBT resins as a function of 1/t1/2

从表3可以看出：CRC和CRP随着pCBT的相对分子质量增加而增大，表明pCBT的结晶速率随着相对分子质量增大而增加，其原因可能是低相对分子质量的pCBT含有较多的链端基，会阻碍聚合物分子链的结晶。

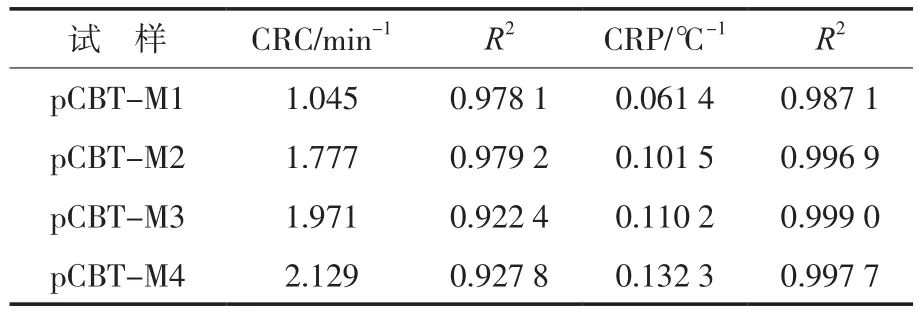
表3 pCBT的CRC与CRPTab.3 CRC and CPR of pCBT resins with different molecular mass

2.2.1 Avrami模型

Avrami模型可以用来描述聚合物的非等温结晶过程，Avrami方程［12-13］见式（5）。

由于晶核的形成和晶体生长受温度变化的影响，所以，在等温和非等温结晶过程中，k和n具有不同的物理意义。从拟合结果可以看出，R2均大于0.999 5（见表2），表明Avrami模型能很好地描述pCBT的结晶过程。

2.2.2 Ziabicki模型

Ziabicki模型扩展了Avrami模型分析，引入了一个包括瞬态和非热效应更为通用的模型来描述非等温结晶过程。Ziabicki等［14-16］认为，聚合物相变动力学可以用一阶的动力学方程来描述［见式（6）］。

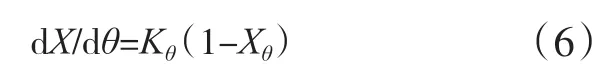
式中：X代表结晶度；Kθ为Ziabicki速率常数；Xθ代表温度θ时的相对结晶度，Kθ和Xθ随温度的变化而变化，取决于非等温过程中的Φ。

Kθ随着温度的变化类似于高斯曲线，可用式（7）描述。

式中：Kmax为最大结晶速率常数；D为DSC结晶曲线半峰宽，min；θm，θg分别为聚合物熔点和玻璃化转变温度，℃。

G为动力学结晶能力参数，用来描述在结晶温度范围内（θg＜θ＜θm）对于一定的Φ下半结晶聚合的结晶能力，按式（8）计算。

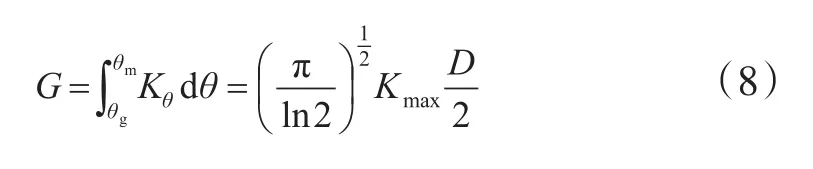
Kmax可用式（9）描述。

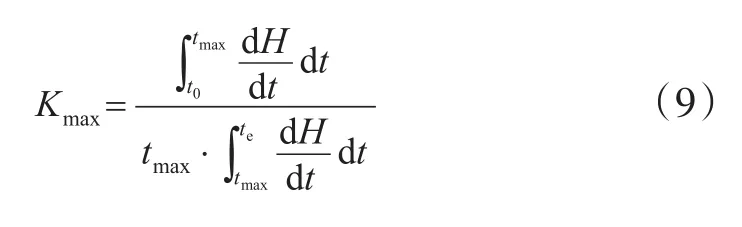
式中：te为终止结晶时间，min；tmax为最大结晶速率时所对应的时间，min；H为某温度区间的结晶焓。考虑到在非等温结晶过程中Φ的影响，G需要进行适当修正［17］，见式（10）。

式中：Gc为单位Φ结晶能力，对同一体系在不同Φ下为常数。

从表4看出：对于不同相对分子质量的pCBT，θmax随着Φ的增加而降低，而在一定的Φ下，θmax随着相对分子质量的增加而增加，在一定Φ下的半峰宽（Dφ）随着Φ的增加而增大，而随着pCBT相对分子质量的增加而减小，Kmax和G随着Φ的提高而增大；随着pCBT相对分子质量的增加，Gc先增加后减小。pCBT-M2的Gc最大，平均值1.09，表明其结晶能力最好，而pCBT-M1的Gc最小，平均值1.00，表明其结晶能力最差。这可能是由于pCBT-M1的相对分子质量较低，其链端基较多，阻碍了聚合物分子链的结晶。pCBT-M4具有较高的相对分子质量，其链端基较少，但其Gc仍然低于pCBT-M2的Gc，表明pCBT-M4较pCBT-M2的结晶能力差，原因可能是pCBT-M4相对分子质量较高，分子链容易相互缠绕，限制了分子链的活动，导致其结晶能力降低。

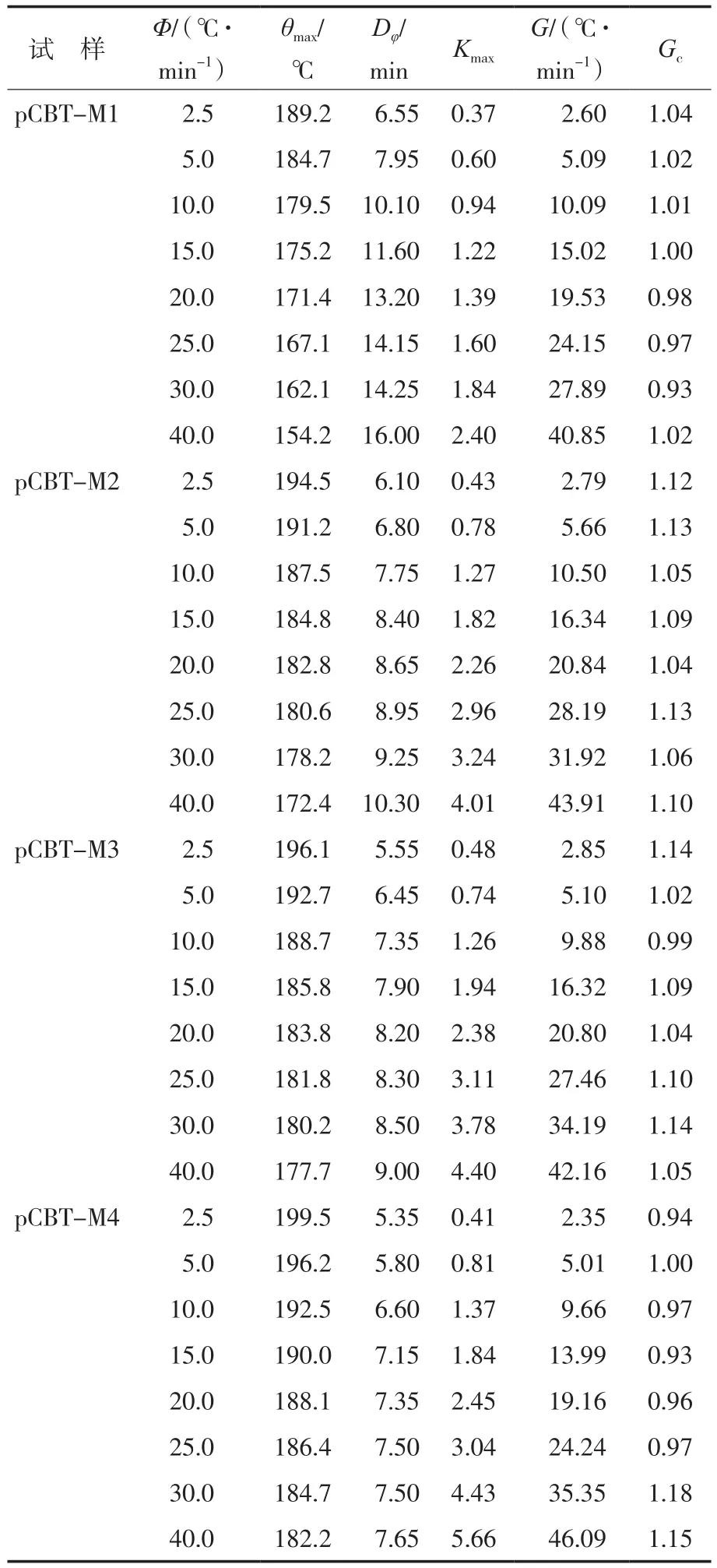
表4 基于Ziabicki模型表征的pCBT非等温结晶动力学参数Tab.4 Non-isothermal crystallization kinetic parameters of pCBT resins based on Ziabicki model

2.2.3 结晶有效能垒

在半结晶聚合物的非等温结晶过程中，通过Friedman［18］的微分等转化率法或Vyazovkin［19-20］的积分等转化率法可以得到聚合物的结晶有效能垒。Vyazovkin积分等转化率中对温度积分取近似值，存在误差问题，因此，采用Friedman微分等转化率法进行计算，Friedman方程用式（11）表述。

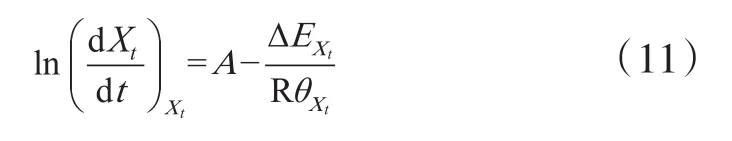
式中：（dXt/dt）Xt为瞬时结晶速率，是时间t在给定Xt下的函数；A为指前因子；R为气体常数；ΔEXt为一定Xt下的有效能垒，kJ/mol；θXt为一定Xt下的温度，℃。在不同Φ下，通过非等温结晶实验得到瞬时结晶速率，然后与相对应的温度倒数做图，得到线性关系，该直线的斜率为ΔEXt/R。

从表5可以看出：pCBT的ΔEXt均随着Xt的增加而增加，说明其结晶能力变差；随着pCBT相对分子质量的增加，ΔEXt先降低然后升高，其中，pCBT-M2的ΔEXt最低，表明pCBT-M2具有最好的结晶能力，与采用Ziabicki模型结晶动力学分析得到的结论一致。

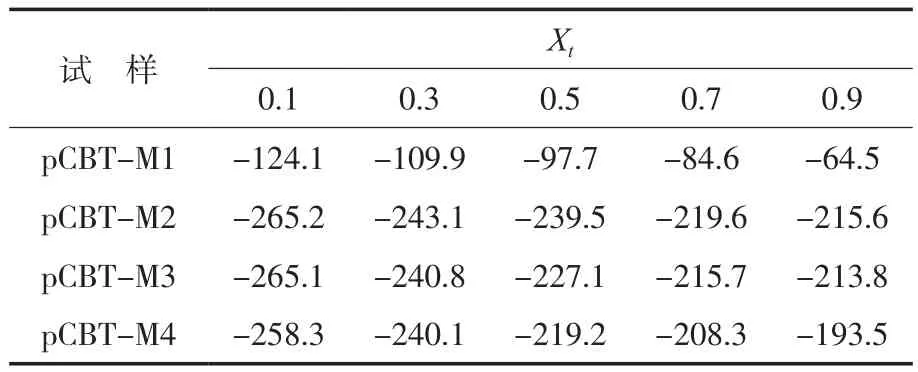
表5 利用Friedman微分等转化率法得到的ΔEXtTab.5 Effective energy barrier ΔEXt obtained by Friedman differential isoconversion method kJ/mol

3 结论

a）采用DSC研究了不同相对分子质量pCBT的非等温结晶行为，发现随着聚合物Mv和Φ的提高，树脂的结晶速率增加。

b）采用Ziabicki结晶动力学和Friedman微分等转化率法分析得出的结果一致，相对分子质量适中的pCBT-M2具有最高的结晶能力。