基于非对称拉普拉斯分布的混合分位数回归参数估计
2021-03-01张发赶何幼桦
张发赶,何幼桦
(上海大学理学院,上海 200444)
传统线性回归要求误差项服从正态分布,然而现实生活中许多数据尤其是金融经济数据大多数是尖峰厚尾的,此时模型的估计结果将不具有稳健性.1978 年Bassett 等[1]提出分位数回归模型.
1986 年,Powell[2]解决了分位数回归中存在缺失数据的问题.1998 年,Thompson 等[3]简单介绍了贝叶斯方法.2001 年,Yu 等[4]进一步完善了贝叶斯方法,完整地将贝叶斯框架引入分位数回归模型中,并使用非对称拉普拉斯分布来描述误差项.2010 年,Taddy 等[5]解决了非参数贝叶斯分位数回归问题.
混合回归模型是研究多个子聚类混合的统计模型.Goldfeld 等[6]首次提出混合回归模型.2014 年,Yao 等[7]和Song 等[8]分别使用t 分布以及Laplace 分布给出新的混合回归模型,相比于传统模型而言,该类模型具有更好的稳健性.Park[9]在混合回归模型中率先将均值和方差综合起来考虑,提出了联合均值方差模型.2016 年,Wu 等[10]提出了混合分位数回归模型.2017 年,詹金龙等[11]利用混合Laplace 分布提出了联合位置和尺度参数的回归模型.
上述研究基本不涉及尺度参数的结构,詹金龙等[11]虽然考虑了尺度参数的结构,但只限于拉普拉斯分布.在实际问题中往往出现不仅类别不同,每个聚类本身也存在差异的情况,例如男女身高的区别,不同学历收入的区别等,基于此本工作提出非对称拉普拉斯分布下的混合分位数回归模型,并同时考虑位置参数和尺度参数的回归问题.
1 混合分位数回归模型
设随机向量y 服从非对称拉普拉斯分布(asymmetric Laplace distribution,ALDp),并且由m 个子聚类混合而成,概率密度函数如下:

对每一个ALDp(yi;µj,),概率密度为

式中:p 为非对称参数,0
若随机变量x 服从ALDp(x;µ,σ2),则有P(x<µ)=p,P(x>µ)=1 −p,即位置参数µ就是分布ALDp(x;µ,σ2)的p 分位数,所以在上述假设下估计模型的参数与求y 的p 分位数是等价的.
在很多情况下,数据本身存在异方差性,这使得传统的混合分位数回归模型的估计存在偏差,针对这种情况,本工作同时对位置参数和尺度参数进行回归,提出了基于ALDp的混合分位数回归模型,

式中:xi={xi1,xi2,···,xir}T和hi={hi1,hi2,···,hiq}T是回归方程的解释变量;相应的{yi}ni=1是独立的被解释变量;βj={βj1,βj2,···,βjr}T是第j 个子聚类中维数为r×1 的位置模型的未知参数;γj={γj1,γj2,···,γjq}T是第j 个子聚类中维数为q×1 的尺度模型的未知参数.βj,γj,πj可以与p 有关,为符号简洁起见,βj即为βj(p),γj即为γj(p),πj即为πj(p).直接求解上述模型是比较困难的,本工作拟采用期望最大化(expectation maximization,EM)算法对上述参数进行估计.
2 基于非对称拉普拉斯分布的EM 算法
EM 算法[12]是含有隐变量的概率模型参数的极大似然估计方法,本工作利用EM 算法对参数进行估计.
假定子聚类数m 是固定和已知的,引入隐变量zij对混合比例进行刻画,若zij属于m 个子聚类的第j 类,则zij等于1;若zij不属于m 个子聚类的第j 类,而属于其余m −1 类中的某一类,则zij等于0.

式(2)在完全数据下关于参数Θ=(β1,γ1,π1,···,βm,γm,πm)T的对数似然函数可以写成

EM 算法是一种迭代算法,流程主要分为两个步骤:E 步和M 步.E 步是计算对数似然函数的期望;M 步是寻找能使E 步产生的似然期望最大化的参数值;重复执行E 步和M 步,直至参数Θ 收敛.具体操作如下.
步骤一 给定参数迭代初始值

步骤二(E 步) 利用第k 次迭代得到的结果估计Θ(k),计算,

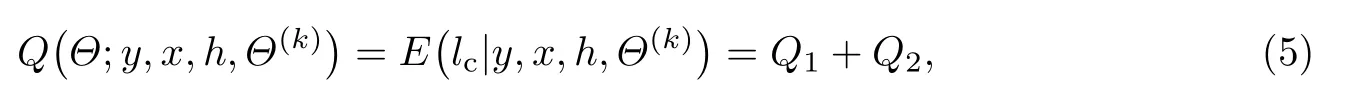
式中:
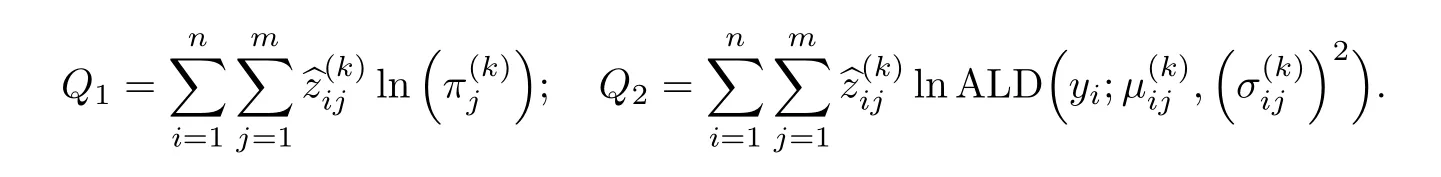
步骤三(M 步) 用Q(Θ;y,x,h,Θ(k))对Θ 求最大值,将得到
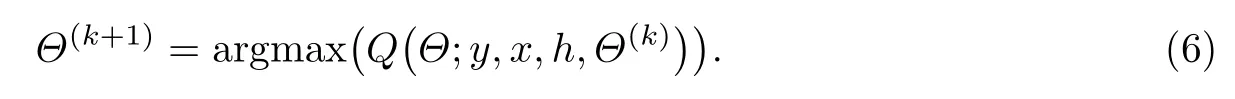
这里采用牛顿法对上述问题进行求解,由于目标函数含有绝对值无法直接求导,因此下文推导过程中对应部分使用差商代替求导,这种做法也方便之后进行数值计算.
令θ=(β,γ),Q(θ)=Q(β,γ),

设计如下迭代过程:

为了计算方便,

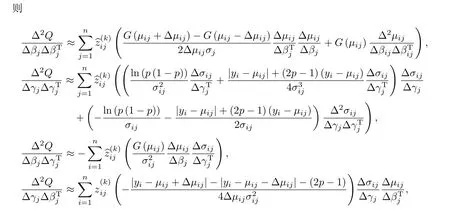
步骤四 重复E 步和M 步,直至参数Θ 收敛.
3 Monte Carlo 数值模拟
利用数值模拟对本工作提出的非对称拉普拉斯分布的EM算法进行验证,以分析样本量和p 对估计效果的影响.
首先,产生服从ALDp分布的n 个随机数,若要产生来自分布F(x)的随机数,需先产生U(0,1)的随机数u,然后计算F−1(u).具体计算步骤如下:(1) 从U(0,1)随机产生u;(2) 计算x=F−1(u),其中F−1(u)=inf{x:F(x)≥u}.
首先求ALDp的累计概率密度函数
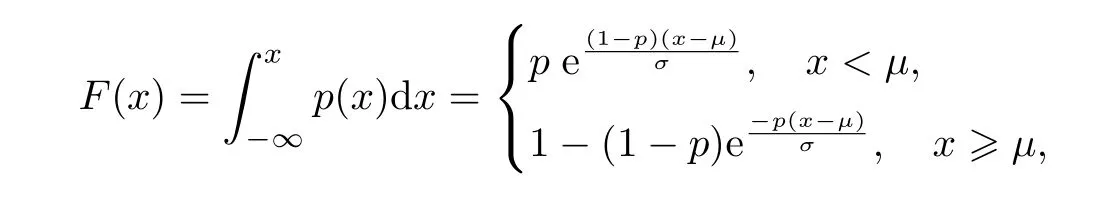
式中:

计算反函数F−1(u),

式中:p 为非对称参数;µ为位置参数,σ 为尺度参数.
通过对不同分类数的模型进行模拟,结果表明样本量和分位数对参数估计精度的影响关系与两分类问题相同.此处仅以m=2 为例,考虑如下混合分位数回归模型:

根据式(11)产生模拟数据,yi服从混合ALDp分布,xi服从U(1,2),hi服从U(1,2),彼此相互独立.考虑分位数对模型参数的影响,即β1=50p,σ1=exp(−p)/5,β2=30p +2,σ2=2p2+0.1,其中p 表示非对称参数.给定混合比例π1=0.3,π2=0.7,取样本量n=100,200,400,600,800,1 000,p=0.1,0.2,···,0.9,重复模拟300 次.利用均方误差(mean square error,MSE)来观察估计效果,结果如表1∼4 所示.

表1 参数β1 在不同样本量下的MSETable 1 MSE of β1 under different sample sizes

表2 参数σ1 在不同样本量下的MSETable 2 MSE of σ1 under different sample sizes
通过计算参数在不同样本量下的均方误差,可以发现模型参数估计的整体MSE 较小,参数估计效果良好.值得注意的是,在小样本下,参数的估计相对于大样本而言精确度会低一些,原因之一是在小样本下高低两侧分位数的数据不足可能会导致部分参数估计的结果存在偏差.但是随着样本量的增加,所有参数在各个分位数下的MSE 均明显降低,说明随着样本量的逐渐增加,模型的估计效果越来越好,并且随着n 的增大,分位数对估计结果的影响也越来越小,模型在各个分位数上的估计稳定性越来越高.显然地,当样本量足够大时,高低两侧分位数也已经拥有了足够多的数据.
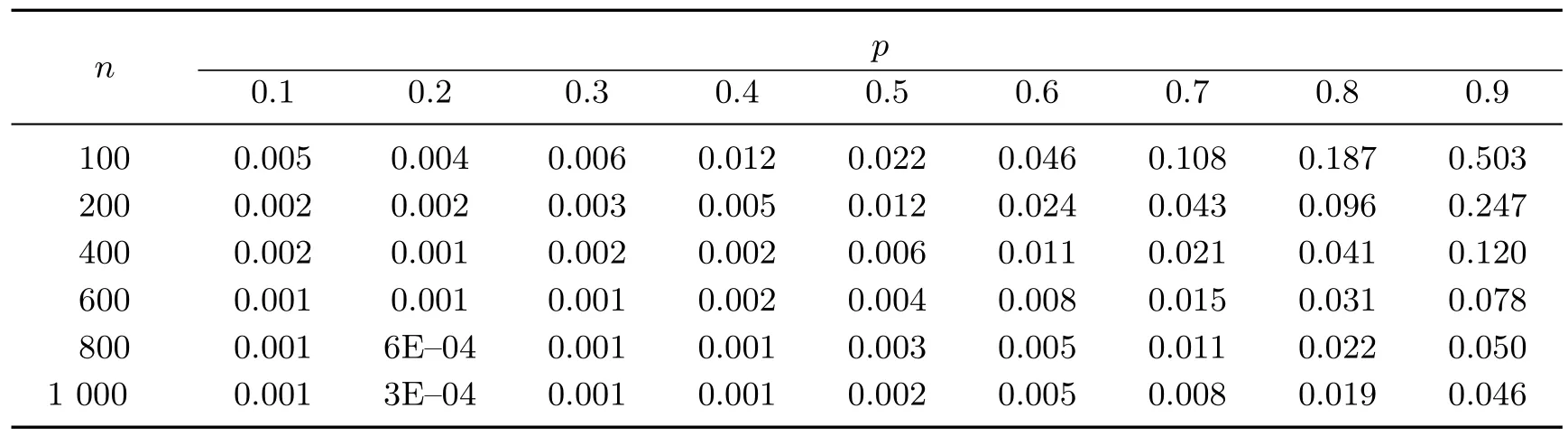
表3 参数β2 在不同样本量下的MSETable 3 MSE of β2 under different sample sizes
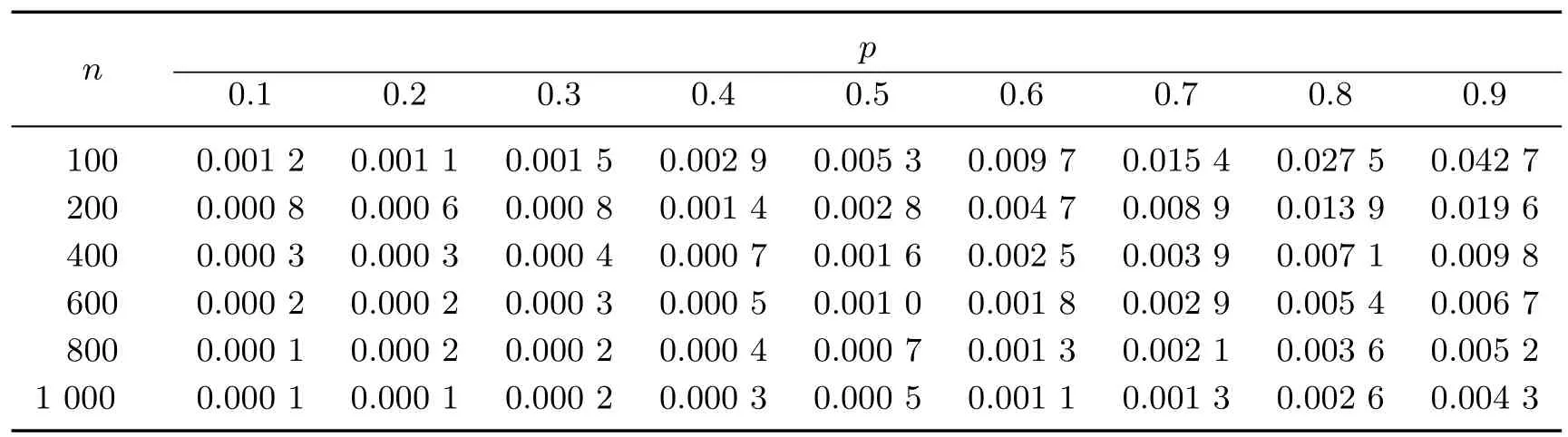
表4 参数σ2 在不同样本量下的MSETable 4 MSE of σ2 under different sample sizes
4 实证分析
4.1 数 据
下面将利用模型(2)对波士顿房价数据进行分析,该数据来源于UCI(University of California Irvine)数据库.波士顿房价数据于1978 年开始统计,包含了波士顿地区房屋的一系列特征(离散变量已由该数据库处理完成),例如犯罪率、一氧化氮浓度、城镇师生比例等,每个特征有506 个样本点.首先对特征进行筛选,通过相关性分析,排除对房价没有影响的变量,进而筛选出其中最重要的两个变量,分别为每栋住宅房间数和该地区房东属于低收入阶层的比例,对应散点如图1 所示.
4.2 模型建立与结果分析
由图1 可以看出,房价的波动与每栋住宅房间数(x1)和该地区房东低收入阶层比例(x2)都有关,利用该数据集构建混合分位数回归模型(12),将数据(房屋)类型分为两类,对这两类数据进行研究发现房价与房间数以及房价与房东属于低收入阶层比例的依赖关系有很大不同.
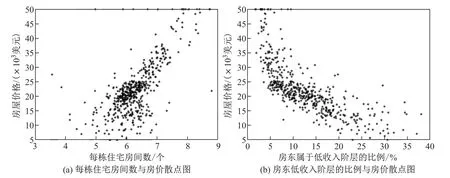
图1 各解释变量与被解释变量散点图Fig.1 Scatter plot of each explanatory variable and explained variable

利用EM 算法对式(12)中的参数进行估计,得到不同分位数下的位置参数和尺度参数估计结果如表5 所示.

表5 不同分位数下模型位置参数和尺度参数以及混合比例的估计Table 5 Estimation of model position parameters,scale parameters and mixing ratio under different quantiles
进一步分析表5 的实际意义,考察不同分位数下解释变量x1和x2对不同类型房屋的房价边际影响如图2 所示.
由图2(a)可知,对于第二类房屋,β21>0,表明该类房屋的房价和房间数的多少呈正相关,并且房间数对房价的边际影响明显高于第一类房屋,但是这种边际影响随着房价的升高逐渐减小.对于第一类房屋,β11在p>0.3 时接近于0,说明此时房间数的多少对房价的影响不大.
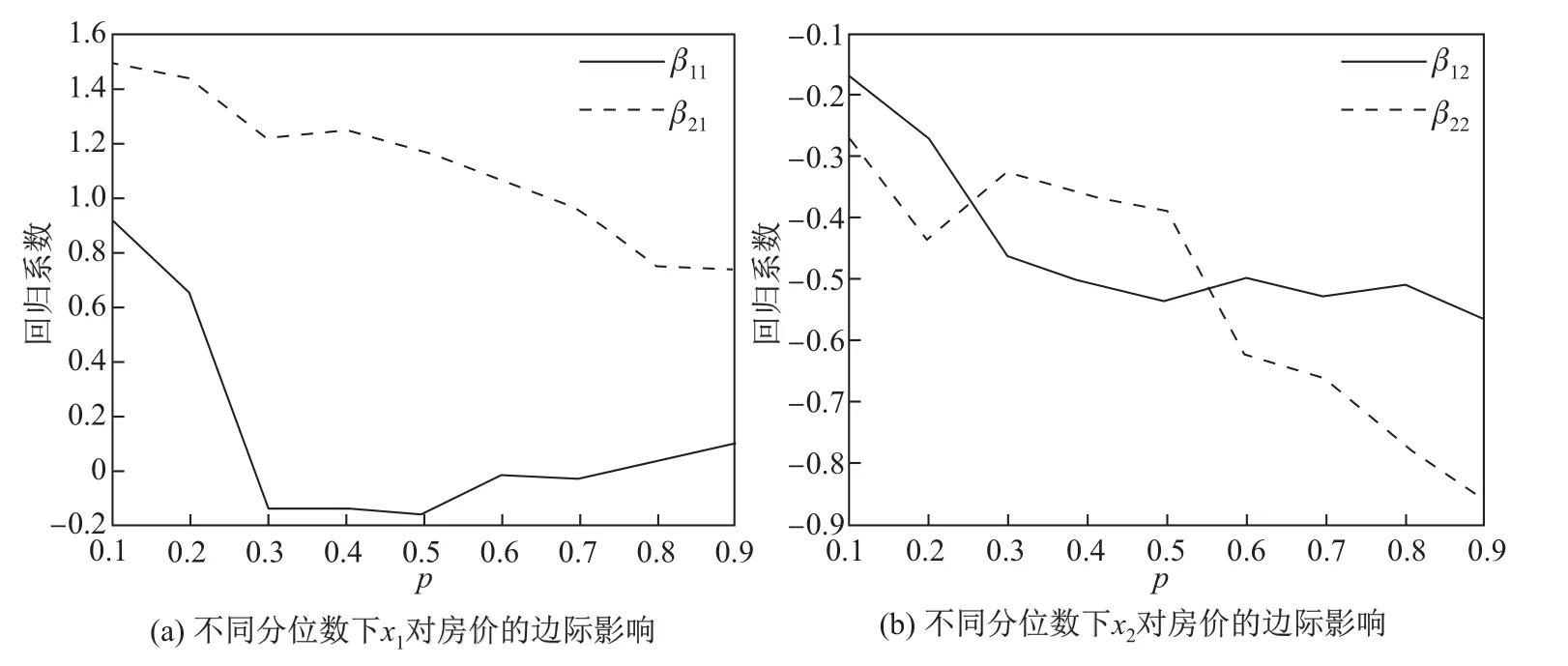
图2 不同分位数下x1,x2 对房价的边际影响Fig.2 Marginal influence of x1 and x2 on housing prices at different quantiles
对于图2(b),β12<0,β22<0,表明在房价的所有分位数点上,该地区房东属于低收入阶层的比例对房价的边际影响是负向的,并且整体而言这种影响会随着房价的升高而逐渐增大,同时第二类房屋的负向影响高于第一类房屋.综上所述,可以将上述房屋分为两类,高档小区和普通小区.对高档小区(第二类)而言,房间数的增加会明显提高房价,可见每个房间的价值都很高,比如市中心的房屋.对于普通小区而言,房间数的多少对房价影响不大,每个房间的价值较低,比如郊区的房屋.同时,对于高档小区而言,随着房价的升高,房间数对房价的边际影响逐渐减小,这表明当房价足够高时,人们会更多地关心居住地的品质,而不仅仅考虑房间的大小.
另一方面,波士顿房东属于低收入阶层的比例会对房价造成负面影响,并且对高档小区的整体负面影响高于普通小区,特别是当房价处于极高的位置时,二者的差距会被进一步放大.这是显然的,高档小区(如别墅)的定位是高收入人群,该区域低收入购房者的比例越高,对此类房屋价格的提高越是不利的,事实证明富人更喜欢和富人居住.
本工作提出的模型相对于传统混合分位数回归模型而言,主要优点在于不仅考虑了解释变量对位置的影响,而且考虑了解释变量对尺度的影响,因此可以在实际运用中对模型的各个部分进行更有效的控制.在实证分析中,使用每栋住宅房间数和该地区房东属于低收入阶层的比例这两个解释变量,对波士顿的房屋价格进行分析,发现每栋住宅房间数对高档小区的正向边际影响高于普通小区,低收入阶层的比例对高档小区的负向影响高于普通小区.随着房价逐渐升高,每栋住宅房间数对房屋价格的边际影响最终会有所降低,而低收入阶层的比例对房屋价格的负向影响会逐渐增大.
