基于改进单神经元梯度学习的无线网络主动队列管理

戚爱春,徐 磊

(1.上海大学机电工程与自动化学院,上海 200444;2.南京中兴力维软件有限公司动环与智能运维产品开发部,南京 211153)

主动队列管理(active queue management,AQM)是链路算法的重点内容,也是主要的研究热点.文献[1]提出了三区域随机早期检测(three-section random early detection,TRED)算法,以便实现时延及网络负载吞吐量之间的均衡.Ko 等[2]提出了fairness-aware delaycontrolled 主动队列管理技术,实现对基于802.11 s 的网络的性能优化.与源端控制算法不同,链路算法主要考虑的是中间节点的情况,考虑到现有网络结构中网络节点众多的特点,链路算法的优越性更加明显[3].

但是随着网络规模的不断扩大,特别是无线局域网(wireless local area network,WLAN)、无线网状网络(wireless mesh network,WMN)等网络类型的增加,网络的服务质量令人堪忧,传统的拥塞控制算法已经无法满足用户需求[4].于是,为了满足不断提高的主动队列管理需求,很多先进的控制理论被应用到AQM 中,如模糊控制[5]、信息压缩[6]、模型预测控制[7].

人工神经网络是通过对神经元系统处理事务的过程进行深入研究得到的,并以计算机为媒介展现出来.人工神经网络具有自适应、自学习、分布并行式处理等优势,不仅被生物学家看作研究生物现象的工具,还被工程师作为解决非线性时变复杂系统的新方法,如今已被广泛应用于各个领域[8].考虑到无线局域网络是非线性、多变且复杂的系统[9],相比于有线网络,在网络拥塞控制方面存在着诸多挑战.此外,由于主动队列管理算法主要应用于传统有线网络,很少应用于无线网络,针对这一现象,本工作首先描述传统有线网络TCP/AQM 数学模型,然后结合无线局域网络的特性,对传统模型进行改进,得到适用于无线局域网络的TCP/AQM数学模型.

在传统的主动队列管理算法中,大部分控制输入均为网络的瞬时队列长度,而瞬时队列长度只能反映当前的网络拥塞状况,忽略了下一时刻网络的拥塞发展趋势.考虑到网络拥塞的真正原因是数据包到达链路的速率高于当前的网络带宽,本工作以此为出发点,增加数据包到达速率作为AQM 算法的输入量,用来反映下一时刻网络拥塞的持续状态,从而提出基于单神经元梯度学习[10]的AQM 改进算法,即改进单神经元梯度学习(improves single neuron gradient learning,ISNGL)算法.本算法通过梯度学习算法动态调整网络参数,并在原算法的收敛速度和稳定性方面加以改进,使得控制效果进一步提升.

1 系统描述

1.1 研究对象及数学模型

本工作主要研究对象是无线局域网络.考虑TCP 的加性增加、乘性减少和队列长度的动态特性,Zheng 等[11]提出了如下TCP/AQM 数学模型,

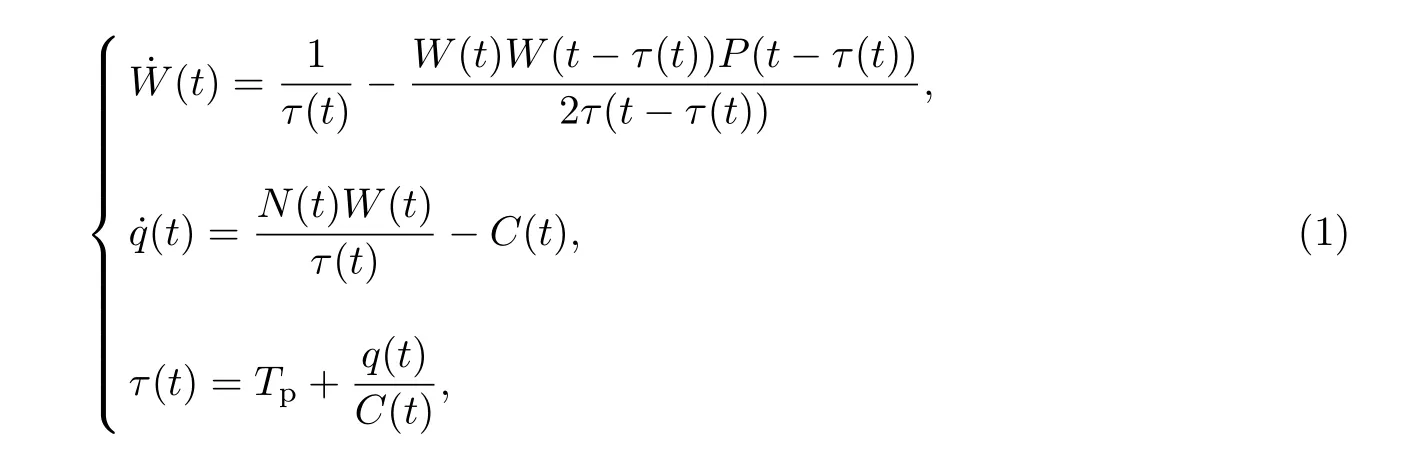
式中:W(t)表示TCP 在t 时刻的拥塞窗口;P(t)表示路由器丢包率；τ(t)表示往返时间;Tp为传输延时;q(t)表示t 时刻的队列长度;N(t)表示网络负载数量;C(t)表示瓶颈链路的容量;上行链路和下行链路的丢包率Pul=Pdl=γ ≪1.

假设在同一时刻,发送端、路由器和接收端之间只有一个链路成功,再结合无线局域网络的特性,对原有模型进行修改,得到以下非线性微分方程:

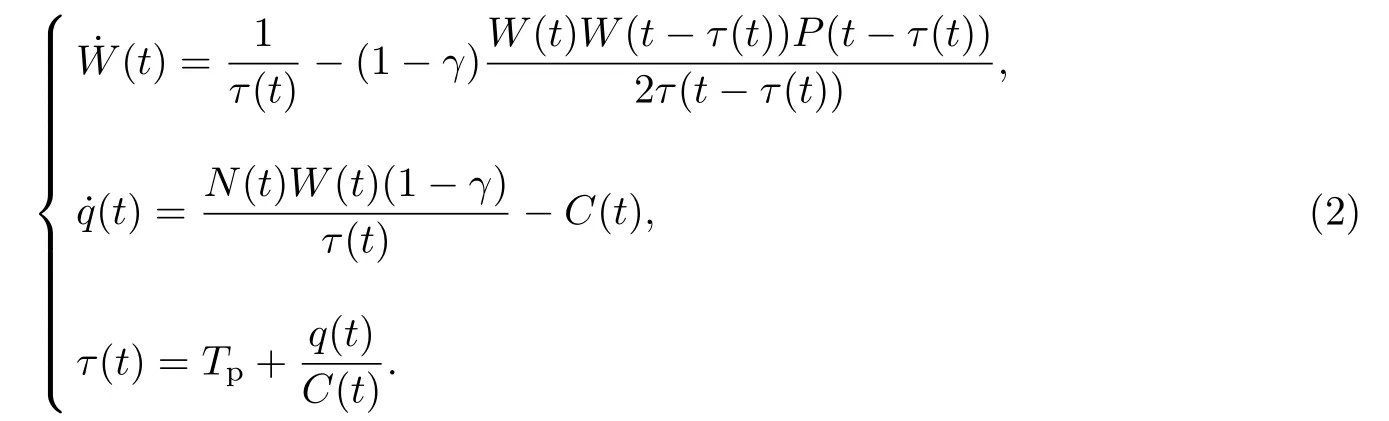
假设在上述模型中,网络负载N(t) 和瓶颈链路容量C(t) 分别为常数N 和C,对平衡点(W0,q0,P0)采用小信号法进行局部线性化和Laplace 变换得到如下传递函数:

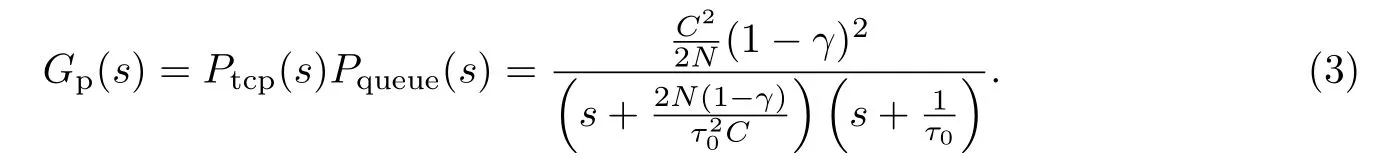
于是,由无线局域网络数学模型可以得到控制系统框图如图1 所示.

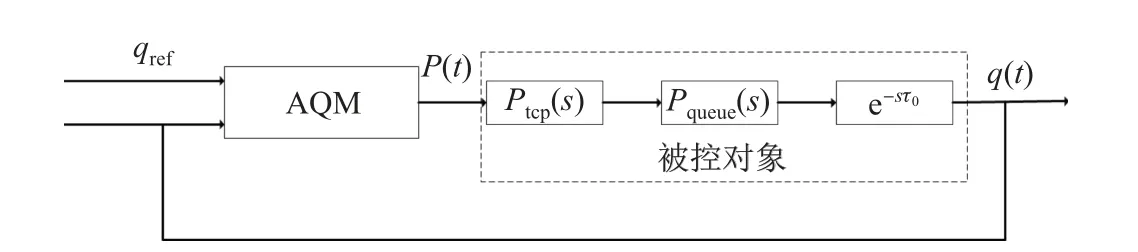
图1 TCP/AQM 控制系统Fig.1 TCP/AQM control system

由于实际无线网络的非线性、时延、参数多变等问题会导致无线TCP/AQM 数学模型不够精确,为此需要设计一个具有动态学习能力的控制器,以提高实际情况中队列长度的收敛性和收敛速度(见图2).

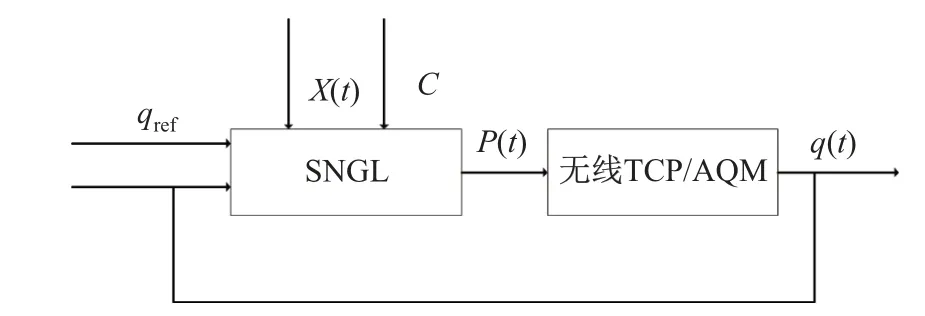
图2 动态学习TCP/AQM 控制系统Fig.2 Dynamic learning TCP/AQM control system

1.2 单神经元AQM 控制器

单神经元AQM 控制器以瞬时队列长度q(t)与期望队列长度qref的误差q(t)−qref作为第一输入,以数据包到达速率x(t)与链路带宽C 的差值x(t)−C 作为第二输入,则可以得到单神经元的输入为e(t)=[e1(t),e2(t)]=[q(t)−qref,x(t)−C].为了采用梯度学习算法来影响输出,本工作为单神经元的输入加上动态调整的网络参数w(t)=[w1(t),w2(t)]T,则单神经元的总输入为

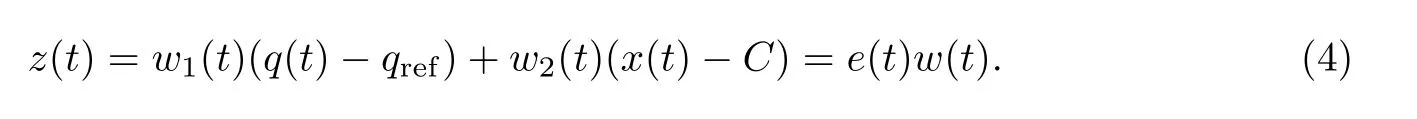
由于无线局域网络的数学模型是非线性的,需要为神经网络引入非线性因素,使其拥有任意逼近任何非线性函数的能力.于是,使用激活函数激活神经元,考虑到存在符号问题,选择与Sigmoid 函数属性相类似的Tanh 函数,则神经元的输出为

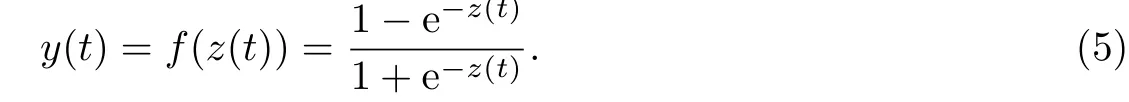
丢弃概率为

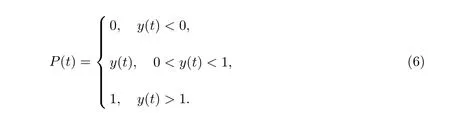
综上所述,单神经元AQM 控制器框图如图3 所示.

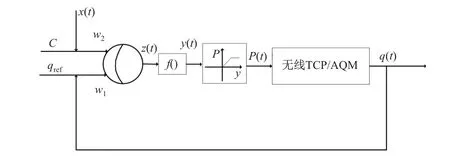
图3 单神经元AQM 控制器Fig.3 Single neuron AQM controller

下面采用梯度学习算法动态调整网络参数w(t).首先,定义系统的目标函数E(t)为

为使队列长度趋于稳定,需要使式(7)取最小值,于是经反向传播学习,系统网络参数w(t)为

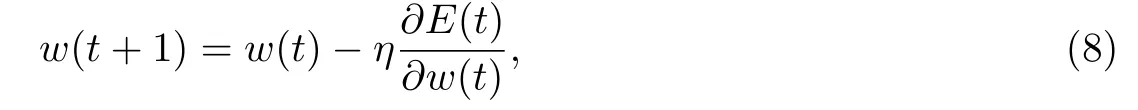
式中:η为学习速率.为了计算梯度方向,可将梯度方向扩展为

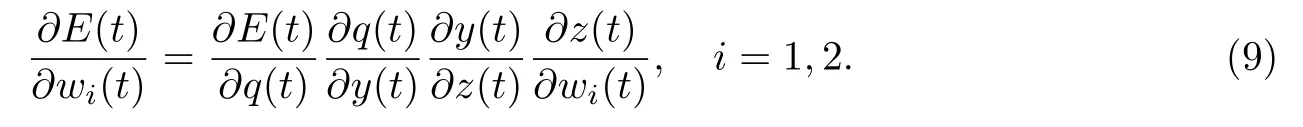
考虑到无线网络的非线性和不确定性,无法直接计算出∂q(t)/∂y(t)的值,于是采用q(t)和y(t)变化值的符号函数来代替,

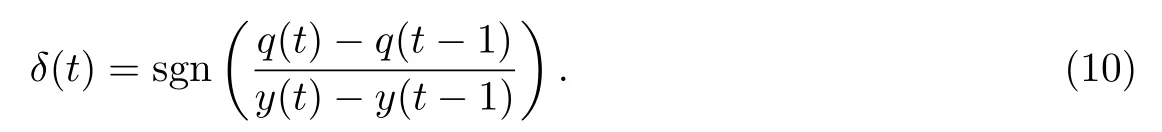
接下来计算y(t)对z(t)的偏导数,得到

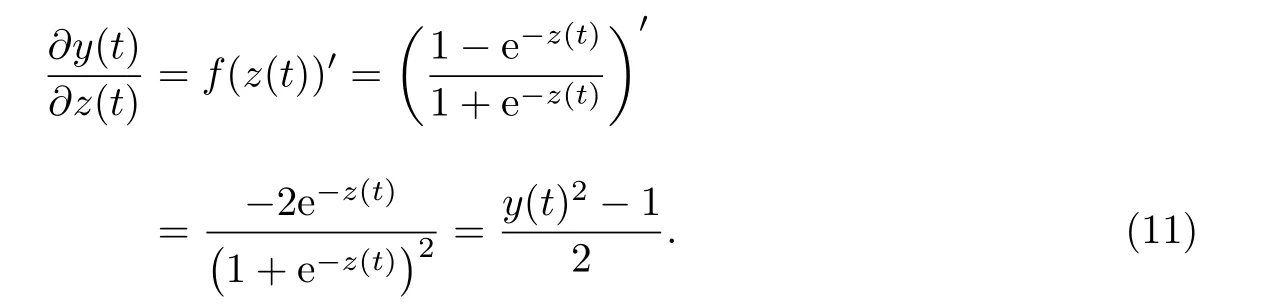
于是网络参数w(t)调整为

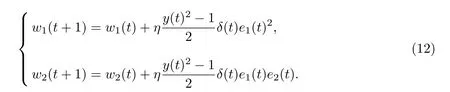
1.3 控制器改进

虽然单神经元控制器相比于传统AQM 控制器在动态调节、控制效果等方面均具有优越性,但是依然存在一些不足.

(1) 平坦区域收敛速度慢.

由于激活函数采用的是Tanh函数,当z(t) →+∞或z(t) →−∞时,f(z(t)) →1 或f(z(t))→−1,这导致f(z(t))′≈0,即进入了平坦区域.而由式(11)和(12)可知,此时无论如何改变学习速率η,权值的调整效果将不再显著,最终导致收敛速度变慢.

(2) 学习时间较长.

由于采用梯度学习算法进行参数动态调整,在学习的过程中,梯度的下降方向一直朝着最快的方向.然而,相对于网络这种实时多变系统,误差值一直都在变化,缺少前期知识的累积,想要达到最优值就需要多次学习,这样往往会增加单神经元的学习时间.

针对上述不足,对单神经元控制器作出以下改进.

(1) 设置带有位移参数的新激活函数.

由式(11)和(12)可知,当学习速率η 一定时,激活函数的导数值越大,权值的调整效果越明显.于是设置带有位移参数的新激活函数为

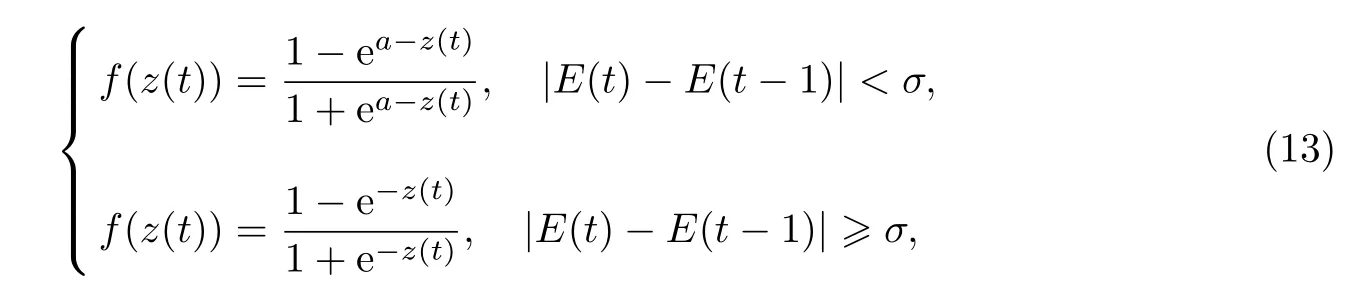
式中:a 为位移参数;σ 为界限值,通常σ 的值比较小.

从改进后的方法可知,当目标函数的变化值小于σ,即进入平坦区域时,使用带有位移参数的激活函数可以使控制器加速越过平坦区域;当处于陡峭区域时,依旧使用原来的激活函数.这样处理有效缓解了平坦区域权值调整效果不佳的问题,从而提高了参数收敛的速度.

(2) 增加权值调整动量.

针对梯度学习算法总是沿着最陡梯度下降,缺少知识积累的问题,本工作引入增加权值调整动量的改进方法.在考虑本次误差调整的梯度方向外,增加上次的调整梯度,使原本沿最陡梯度方向调整改为沿误差曲面的平均方向调整,并不断累加调整动量,为后续学习提供知识积累,缩短学习时间.于是权值调整公式为

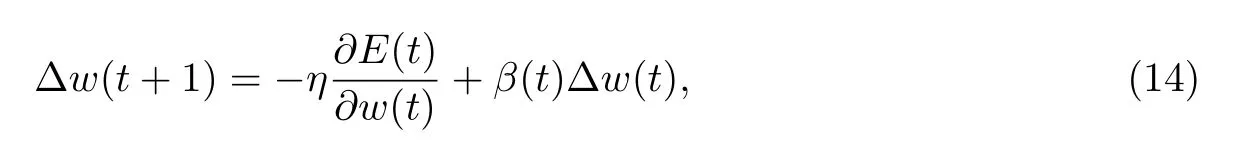
式中:β(t)∆w(t)为权值调整动量;β(t)为动量系数,通常0<β(t)<1.

在实际网络中,当误差逐渐变小并接近期望值时,说明误差修正的方向是正确的;反之,当误差逐渐变大并偏离期望值时,说明误差修正的方向是错误的.为了使权值调整动量更加精确,考虑到并非所有的梯度方向都是完全正确的,本工作将权值调整动量中的动量系数进行动态变化,并采用模糊控制来动态调整.

设模糊控制的输入值为q(t)与qref的误差值变化de(t)以及目标函数的变化dE(t),

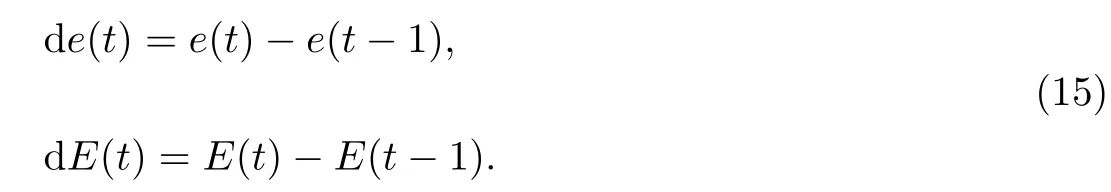
将系统输入值de(t)和dE(t)的模糊区域设为[–4.5,4.5],将模糊集划分为7 个子集,分别为负大(NB)、负中(NM)、负小(NS)、零(Z)、正小(PS)、正中(PM)和正大(PB).隶属度函数采用高斯型,

式中:ci和bi分别为隶属度函数的中间点和宽.

在t 时刻,模糊控制的输出为K(t),则其模糊集也划分为7 个子集,分别为非常小(TS)、很小(VS)、小(S)、中(M)、大(B)、很大(VB)、非常大(TB),对应的论域为{a1,a2,a3,a4,a5,a6,a7},其中ai(i=1,2,···,7)为相应的值.

假设模糊规则之间的关系是局部的,于是建立如下模糊规则:

这里通过max-min 复合运算合成规则,则模糊规则如表1 所示.

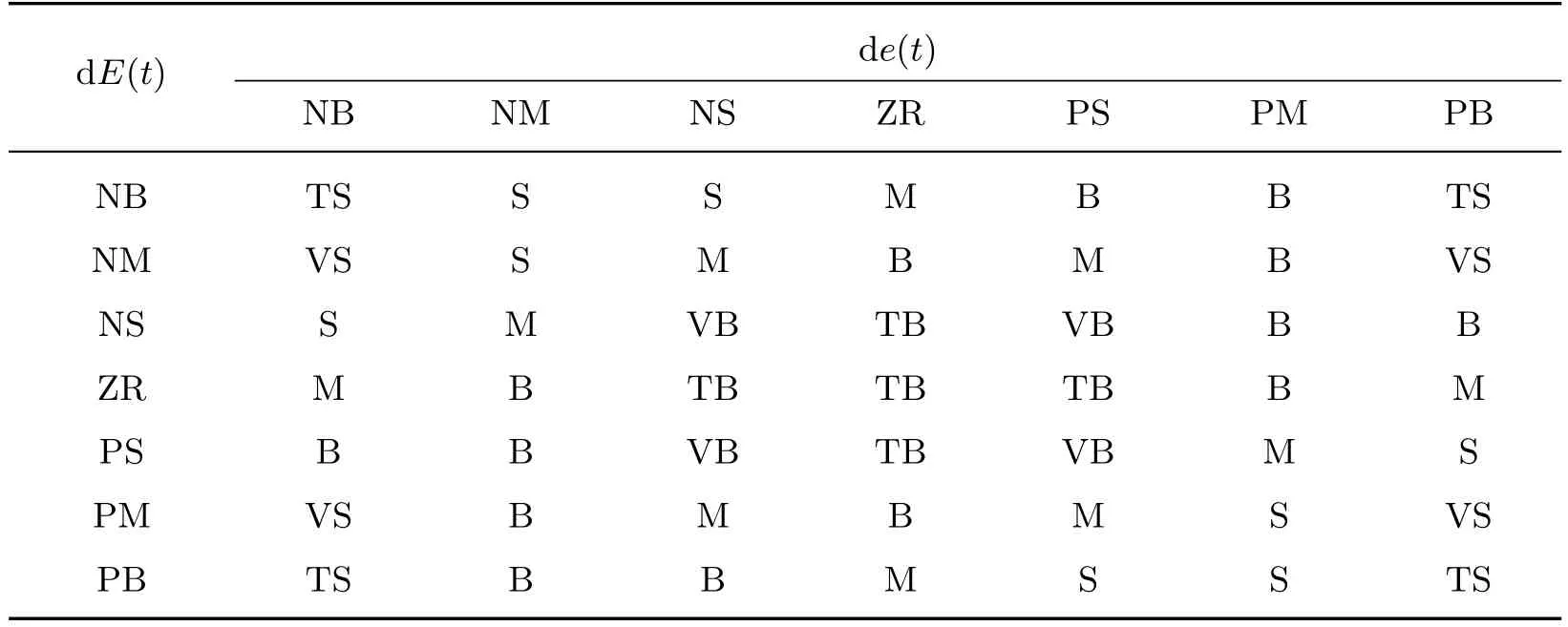
表1 模糊规则Table 1 Fuzzy rules

通过重心法去模糊得到输出,则神经网络的学习速率为

这样,权值调整动量将以准确的动量系数进行动态附加,改进了误差修正方向,同时为后续学习提供了知识积累,缩短了学习时间.

需要说明的是,本工作考虑了上行链路和下行链路的丢包率远小于1 的情况.考虑到TCP 的稳定性,当丢包率接近1 时,会导致发包率增加且网络更早地进入拥塞状况.此时,本工作所提出的方法仍然可行,为简要起见,略去相应结果.

2 仿真与分析

为了验证ISNGL 算法的性能,利用网络模拟软件NS2 对算法进行仿真研究.在NS2 中,搭建如图4 所示的网络拓扑结构.

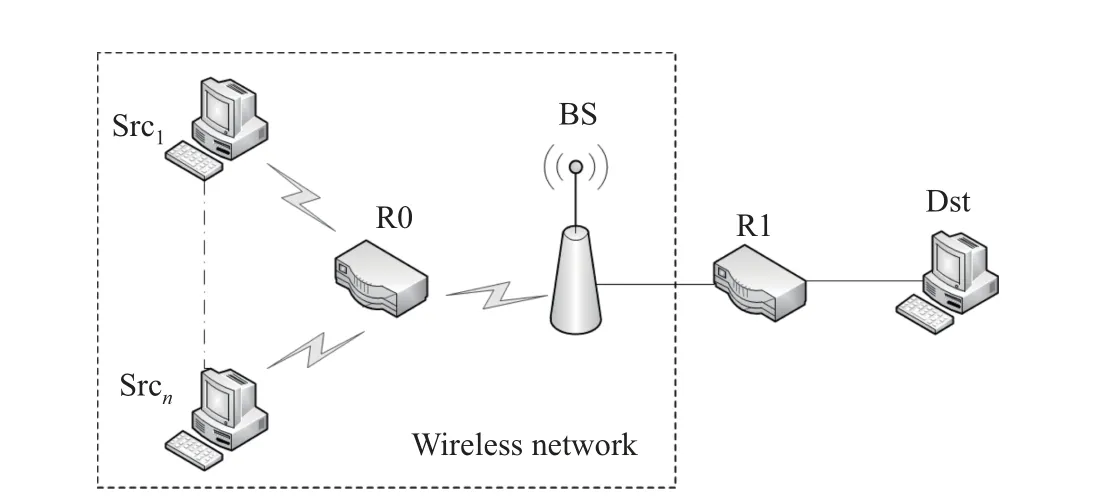
图4 网络拓扑结构Fig.4 Structure of network topology

图4 中:BS(base station)为基站;R0 和R1 分别为无线域和有线域路由器;Src1∼Srcn为数据发送的源端,这里源端数量为20 个;Dst 为数据接收端.Dst 和R1 之间的链路带宽为10 Mbit/s,时延为10 ms;BS 与R1 之间的瓶颈链路带宽为10 Mbit/s,时延为20 ms.设上下链路的丢包概率为0.01,传输的数据包大小为500 bytes,最大队列长度为300 packets,期望队列长度为100 packets.仿真时间为240 s.

对于ISNGL 算法,设置参数a1=0.4,a2=0.6,a3=0.65,a4=0.7,a5=0.75,a6=0.8,a7=1.0,a=2.0,σ=2.5,w1=0.000 005 601 9,w2=0.000 002 654.

实验一:为了验证ISNGL 算法在维持瞬时队列长度稳定性方面的性能,将ISNGL 与其他算法进行对比,则队列长度变化如图5 所示.由于无线路由器先要与基站进行链接,所以源端的数据在几秒钟以后才开始传输.

瞬时队列长度是链路缓存区中等待分组转发的数据包的数量,在AQM 算法中是检测网络拥塞的重要指标.从图5 可以看出,ISNGL 算法在队列长度稳定性方面要优于其他算法.由于设置了带有位移参数的新激活函数并增加了权值调整动量,相较于以往的SNGL 算法,ISNGL 算法队列长度的收敛速度提高,学习时间缩短.因此实验结果验证了ISNGL 算法的有效性.

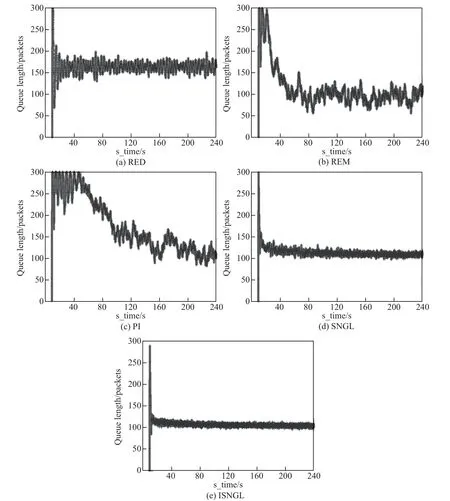
图5 ISNGL 算法和其他算法的瞬时队列长度Fig.5 Instantaneous queue length of ISNGL algorithm and other algorithms

实验二:为了验证ISNGL 算法对突发数据流的适应性,考虑如图6 所示的实验,n 为源端开始数量.

由图6 可见,当网络中出现突发性数据流时,瞬时队列长度会有明显的抖动,而当网络中的数据流减少时,瞬时队列的长度同样也会抖动,但是没有数据流增加时的抖动程度大.即便有明显抖动,ISNGL 算法还是能够在较短的时间内将队列长度收敛于期望值附近.当网络负载稳定时,队列长度也能够保持相对稳定,这说明ISNGL 算法在网络中出现爆发性增减数据流时有较好的适应性.

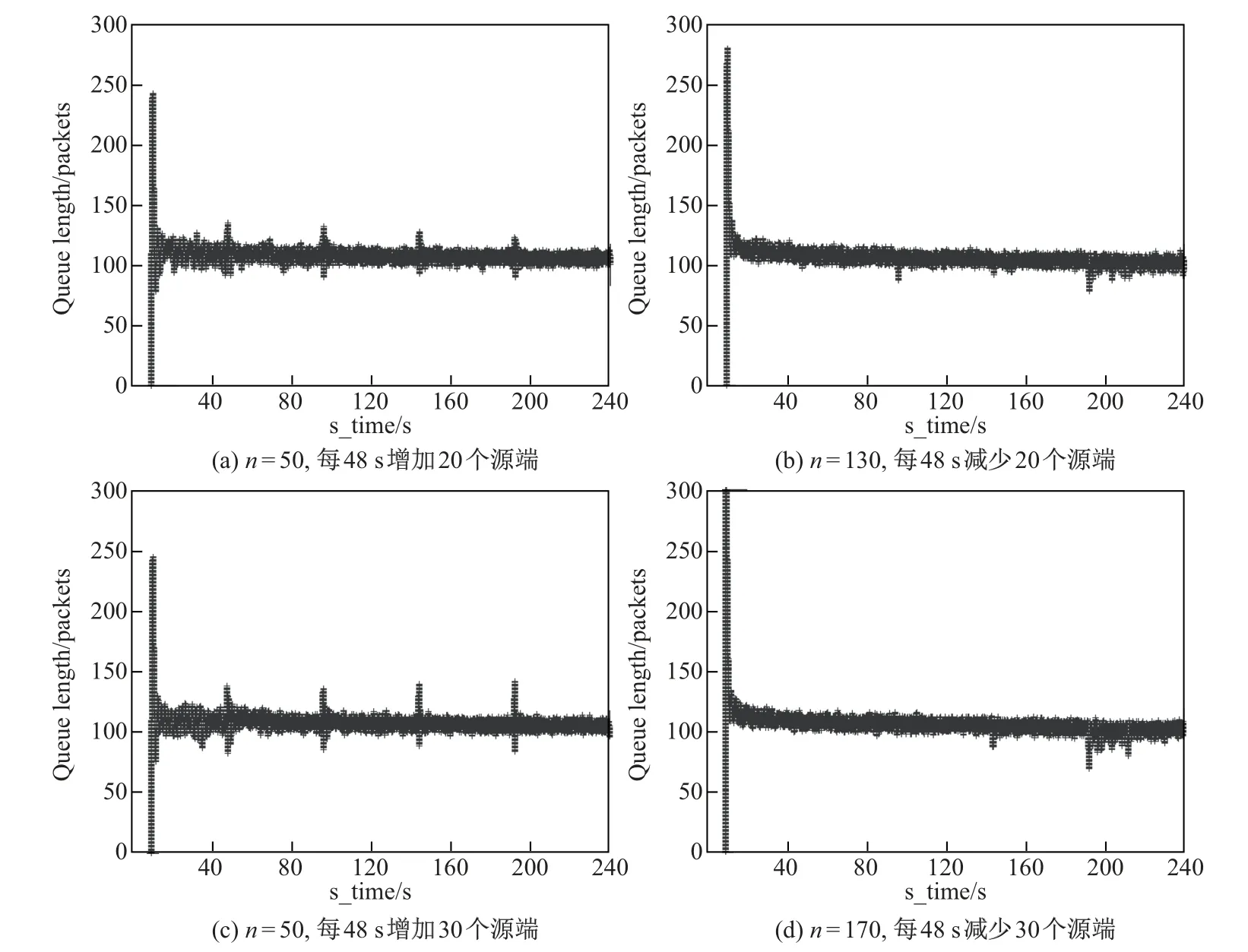
图6 动态负载下的瞬时队列Fig.6 Instantaneous queue under dynamic loads

3 结束语

本工作针对传统AQM 算法忽略下一时刻网络拥塞发展趋势的问题,引入数据包到达速率作为输入量,提出了基于单神经元梯度学习的AQM 改进算法.首先介绍了单神经元梯度学习的原理,从中分析其在收敛速度和学习时间方面的不足,提出了带有位移参数的激活函数和融合模糊控制的权值调整动量项的改进,使算法在控制效果上得到进一步提高.NS2 仿真结果表明,相比于常见的AQM 算法,ISNGL 算法可以更好地将瞬时队列长度收敛于期望值附近,稳定性更高;同时,ISNGL 算法对于突发数据流也具有较强的适应性,而且在大延时或动态变化的环境下也能够迅速调整网络参数,控制效果显著.