晶体塑性有限元分析开孔对多晶板材力学性能的影响
2021-03-01胡晓郁都亚鹏楚海建
胡晓郁,都亚鹏,楚海建,2
(1.上海大学上海市应用数学和力学研究所,上海 200072;2.上海大学理学院,上海 200444)
材料的塑性行为是材料的基本性能,对工程结构的可靠性与安全性具有重要意义.如何准确模拟实际材料的塑性行为一直是计算力学研究的重要方向.在传统上,基于宏观的实验现象和假设,人们建立了许多不同的屈服准则,对于金属材料,比较典型的有最大切应力屈服准则和Mises 屈服准则等.在微观上,位错运动和孪晶是金属材料发生塑性变形的主要机制.基于此,学者们提出了基于微观变形机理的晶体塑性理论.有限元方法是分析材料塑性行为的一种有效方法,在一些流行的商用软件(如ABAQUS、ANSYS 等)中,将宏观的屈服准则内置于程序中,相关应用往往已经标准化.然而,在晶体塑性理论的有限元程序化方面则相对滞后,目前还没有一款通用的晶体塑性有限元软件.由于晶体塑性理论计及了材料微观变形机理,能够更加准确地反映材料实际塑性变形过程,学者们在晶体塑性有限元的研究方面进行了有益的探索.Nakamachi 等[1]开发了早期的晶体黏塑性有限元程序,研究板材的冲压性能.Wu 等[2]采用晶体塑性理论,通过比较原始应变片和预应变片之间的流动应力与取向曲线的差异,研究了预应变对材料各向异性的影响.冯露等[3]用ABAQUS 的UMAT 子程序编写材料的本构,提出一种有效的求解单晶材料黏塑性模型的方法.需要指出的是,在上述研究报道中,关于孪晶效应往往较少涉及.而孪晶是一种较为常见的塑性变形机制,如卢磊等[4]综述了纳米孪晶金属材料的塑性变形机制,通过分析纳米孪晶结构变形时可启动的滑移位错类型,揭示纳米孪晶金属塑性变形的3 种位错机制.王晓东等[5]基于TWIP 钢在不同形变温度下微观组织的特征和引入的特征温度的方法,研究孪晶诱发塑性钢中的马氏体相变及高塑性机制.由此可见,在晶体塑性有限元中计及孪晶变形机制具有重要意义.另一方面,孔洞是材料体内经常出现的一种缺陷,对材料力学性能的影响不容忽视.如Shu[6]使用黏弹塑性晶体理论研究了含孔洞单晶材料的变形,研究结果表明小孔洞长大的趋势要小于大孔洞.Orisini 等[7]应用率相关的晶体塑性模型研究了FCC 单晶铜的孔洞长大模式,研究结果表明晶体转动和塑性滑移区域主要集中在孔洞附近.O’Regan 等[8]使用传统的二维有限元模型模拟研究了不同孔洞百分比、加载条件和晶体取向对孔洞长大的影响.对于板材的开孔,王秀丽等[9]对梁腹板上开孔的节点形式进行反复荷载试验,探讨了梁柱节点区域内截面应力分布规律、滞回性能节点破坏模式及极限承载能力,并利用ANSYS 进行详细计算和对比分析.全栋梁等[10]对单双层多孔层板进行流阻特性和冷却有效性试验,结果表明对于多孔层板,流阻的大小和冷却有效性的高低主要取决于多孔层板的开孔率,开孔率越大,流阻越小,冷却有效性越高.周艳秋[11]研究了梁腹板特殊开孔引起的应力集中问题,应用有限元法分析了开孔的垂向位置、孔的宽度、孔的长度对强梁整体强度的影响,以及最大应力发生位置的变化规律.Li 等[12-13]通过晶体塑性有限元方法(crystal plastic finite element method,CPFEM),研究了变形-微观结构演变-机械响应之间的相互作用,以及晶界变形对裂纹萌生和扩展的影响.而采用晶体塑性有限元方法开展开孔板材力学行为的研究则鲜有报道,有必要开展此方面的研究.
本工作将位错运动和孪晶变形机理引入晶体塑性有限元模拟中,基于ABAQUS 仿真计算平台,通过编写VUMAT 子程序,实现将微观尺度上的位错理论映射到宏观的塑性变形.运用本方法,对FCC 多晶铜材料进行模拟研究,系统性分析开孔尺寸、双孔相互作用及其排布方式对板材抗拉强度和延展性的影响.
1 晶体塑性理论
在经典的塑性理论中[14-16],材料的变形行为可以分解为弹性变形和塑性变形两部分,即

式中:F 表示变形梯度,下标e 和p 分别代表弹性和塑性.材料中位错滑移等行为是塑性变形的主要微观机理.塑性变形的过程可表示为
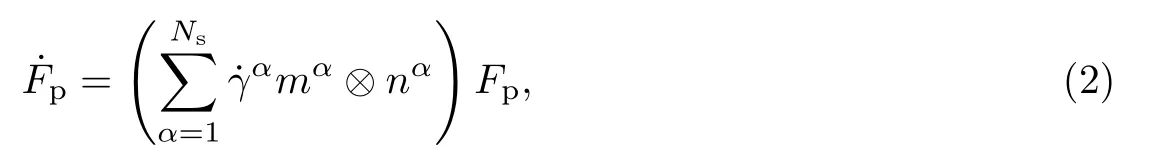
相应的格林应变张量为
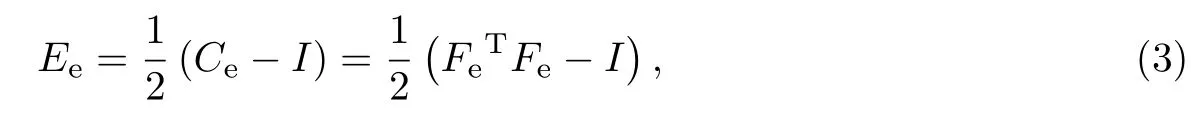
式中:I 是二阶单位张量;Ce为右Cauchy-Green 应变张量.
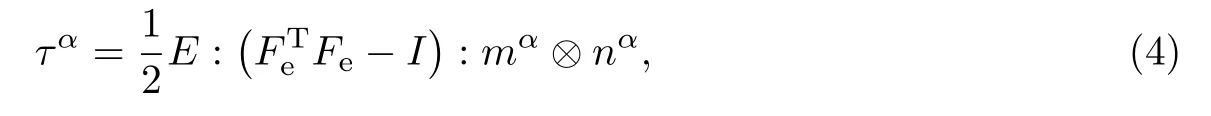
式中:E 是材料的刚度张量.
已有大量研究[17-20]表明,在位错的演化机制中,剪切滑移率与剪切应力和位错滑移阻力密切相关,

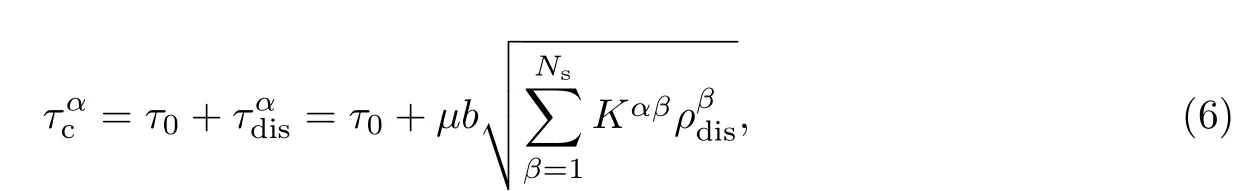
式中:τ0表示内在晶格阻力;表示位错网络引起的硬化效应[21];µ是剪切模量;b 是伯格斯矢量的大小;Ns是滑移系的数量;Kαβ是位错的相互作用系数;是在β 滑移系上的位错密度.
此外,Kαβ可以表示为
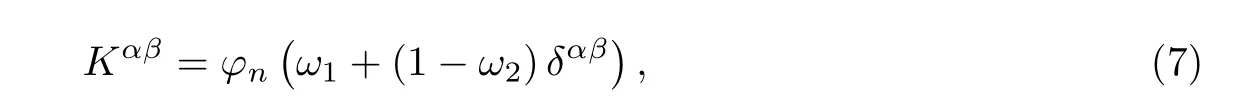
式中:φn是位错硬化系数;ω1和ω2是位错间相互作用系数;δαβ是克罗内尔符号.
由于位错的演化涉及位错的增殖和湮灭过程,所以位错密度的变化需要分为两个部分进行叠加.根据已有研究[21-22],位错密度的演化可以表示为
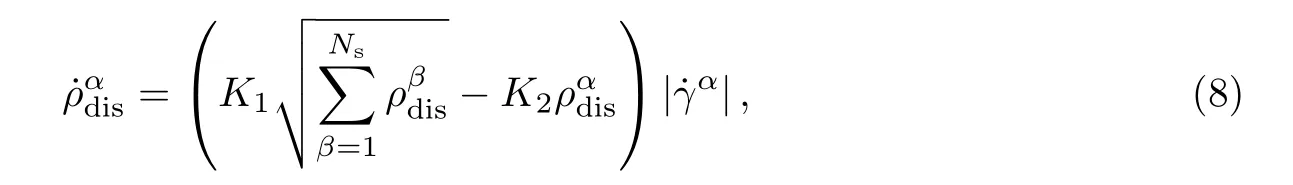
式中:K1和K2分别对应位错产生和湮灭.
孪晶是金属晶体多晶材料重要的塑性变形方式.当孪晶机制被激活时,材料的塑性变形就包含了位错演化和孪晶演化两种机制,相应的速度梯度Lp可表示为[23]
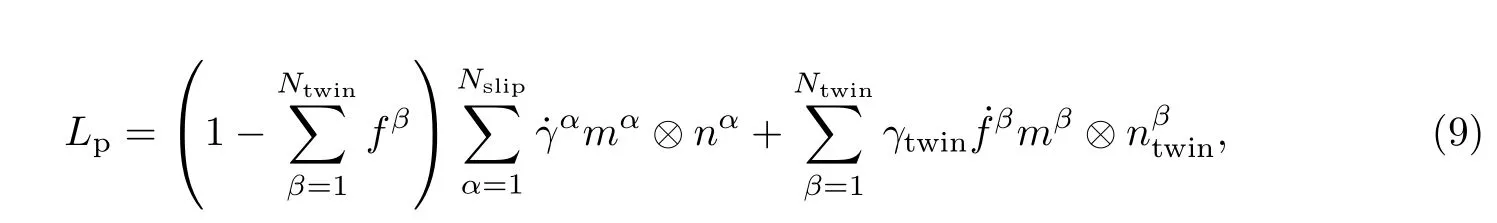
式中:Ntwin和Nslip分别是孪晶系和滑移系的数量;γtwin表示孪晶剪切特征值;fβ是β 孪晶系的体积分数;是β 孪晶系产生孪晶的速率,代表孪晶体积分数的演化.根据Kalidindi[24]的研究,孪晶体积分数的演化可表示为
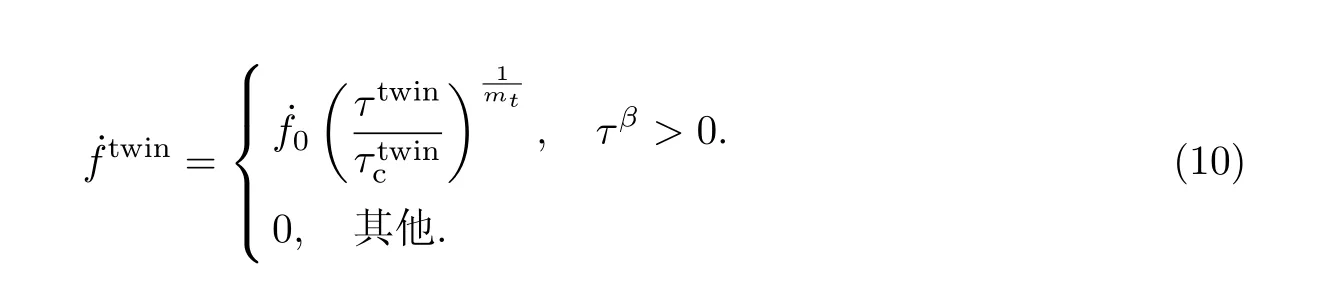
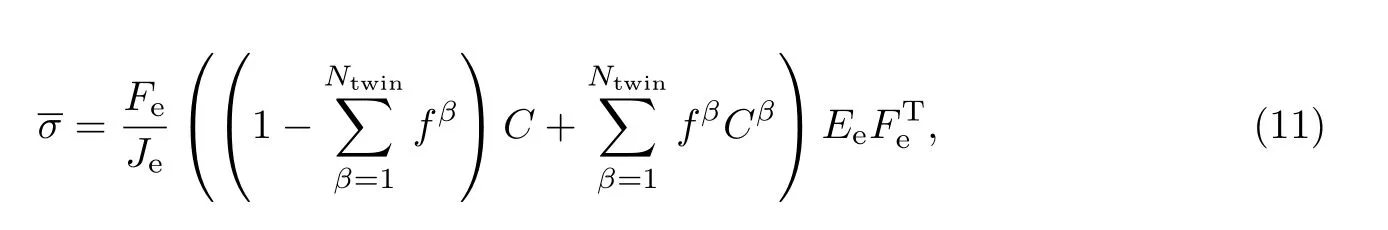
2 试验验证有限元模型
通过ABAQUS 有限元软件所提供的子程序VUMAT 将上述理论程序化.为验证合理性,将所得计算结果和试验结果与传统有限元模拟结果进行对比分析.试验所选用的材料为多晶铜,试样尺寸根据GBT 34505—2017 标准选取.铜圆柱体为全截面试样,直径d=10 mm,长度L=120 mm.铜圆柱体单向拉伸试验由中机电子万能试验机DWD-100A 完成.试件一端固定,另一端施加位移荷载,拉伸速率为0.02 mm/s.
在传统有限元分析中,材料的失效采用Mises 屈服准则,并且假定材料为各向同性材料.采用双线性等向强化模型,根据试验得到的应力应变曲线设定参数并进行有限元模拟计算.
在晶体有限元模拟中,采用三维六面体减缩积分单元(C3D8R),共5 096 个.位错滑移系采用(111)[101],共12 个.材料的初始位错密度为1.27×1015mm−2,弹性模量为115 MPa,泊松比为0.34.根据试验的实际边界条件,设定有限元模型的边界条件如下:圆柱模型一端为固定端,限制其6 个自由度;另一端施加位移荷载,拉伸速率为0.012 mm/s.VUMAT 中使用的其他详细参数如表1 所示.
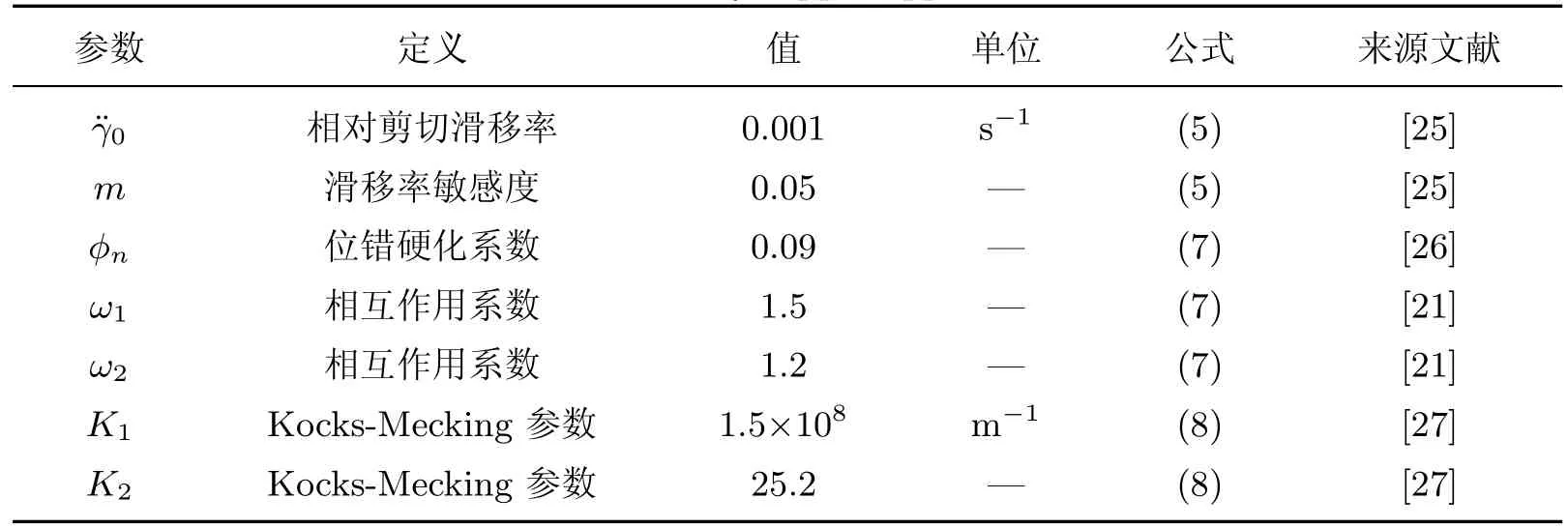
表1 合金铜在CPFEM 模型中应用的参数Table 1 Parameters of alloy copper applied in CPFEM model
多晶模型则由软件Neper[28-30]建立,共有400 晶粒,晶粒平均尺寸约为2.87 mm,晶粒为随机取向.如图1 所示,不同色块代表不同晶粒.
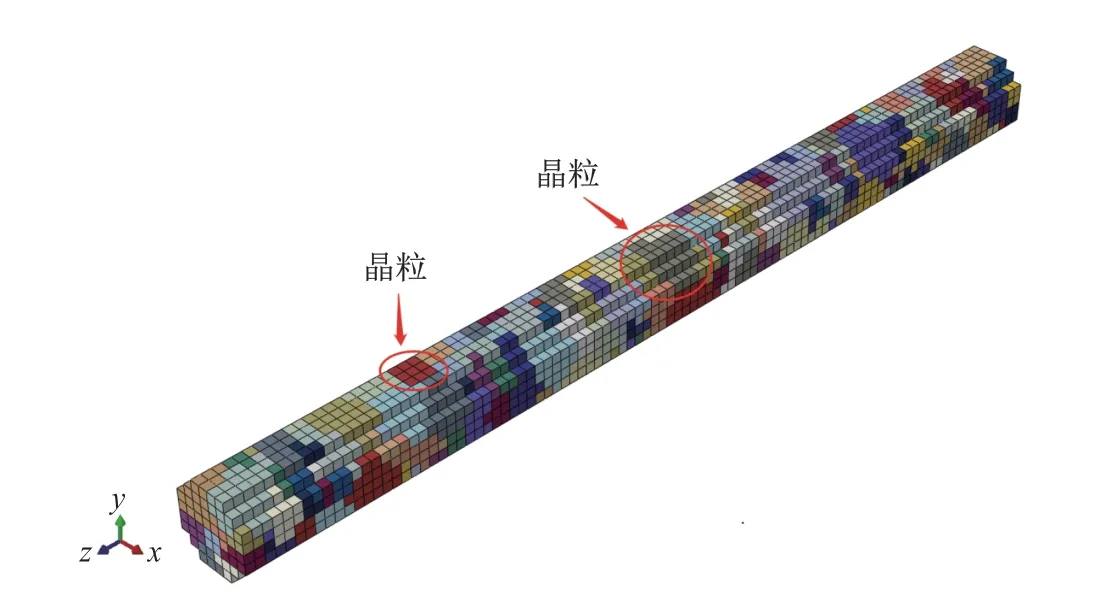
图1 Neper 建立的多晶体模型Fig.1 Polycrystal model generated by Neper
有限元模拟结果与试验结果如图2 所示.一方面,由图2(a)可以看出,无论是采用传统有限元方法(Mises 屈服准则)还是采用晶体塑性有限元方法,都能很好地拟合试验结果,证明了本工作开发的晶体塑性有限元方法的可靠性.另一方面,从图2(b)和图2(c)的Mises 应力云图对比中可以发现:①图2(b)中非颈缩区域的应力沿轴线分布较为均匀,材料表面也较为光滑,无明显应力集中区域,由端面到颈缩区域的应力分布可看作阶梯型分布;②图2(c)中无论是颈缩区还是非颈缩区,应力沿轴线分布呈现明显的非均性,由端面到颈缩区域的应力分布呈现出云朵状,材料表面出现一些不平整的区域.一般来说,材料的各向异性包括两个方面,一是实际材料或晶粒弹性常数(如刚度张量)的各向异性,二是晶粒滑移系取向不同引起的各向异性.而传统有限元分析无法将滑移系引起的各向异性考虑进去.在本工作的分析中,将传统有限元方法的弹性常数设为各向同性,因此在非颈缩区应力分布呈现均匀状态;而应用晶体塑性有限元方法时,将材料划分为400 个大小不一的晶粒并赋予随机的晶体取向,当材料发生塑性屈服时,部分晶粒由于对应滑移系上切应力过大,位错容易滑移,而部分晶粒由于滑移系上切应力过小而未开动,这样就导致材料体内应力分布和变形的非均匀性,因此材料表面出现不平整现象.由此可见,两种有限元方法呈现出不同的应力与变形现象,这是由模型本身决定的.而实际中大块晶体材料多为多晶材料,其晶粒塑性变形的各向异性是由材料本身微观机制决定的,因此采用晶体塑性有限元方法更能反映材料实际变形过程.
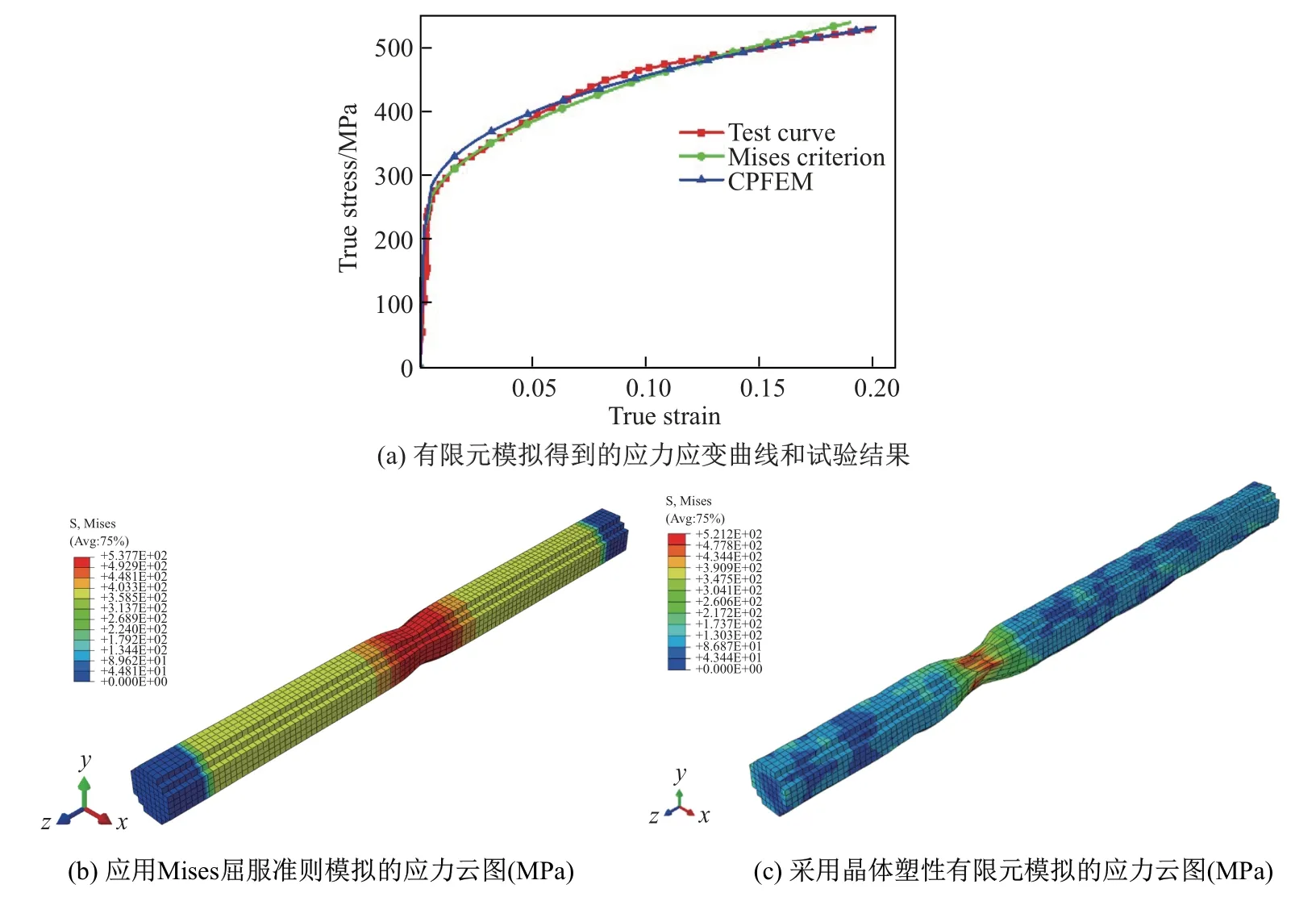
图2 多晶铜板单轴拉伸ABAQUS 模拟结果Fig.2 Simulation results for the polycrystal copper plate under uniaxial tensile load by ABAQUS
3 开孔多晶铜材料性能模拟
在板材的实际应用中,开孔经常出现在各种金属加工中.由于孔洞的引入,容易在孔的周边引起应力集中,导致构件许可荷载的降低,影响结构的可靠性与安全性.而采用计及晶粒取向及其微细观变形机理的晶体塑性有限元方法研究此问题则鲜有报道.因此,本工作将主要从开孔孔径的尺度、双开孔孔距以及双开孔位置排布三个方面进行分析.
3.1 孔径对力学性能的影响
模型尺寸为30 mm×10 mm×2 mm,在正中间开不同直径(D)的圆孔,如图3(a)所示.边界条件设为一端是固定端,另一端是拉伸端(拉伸速率为0.01 mm/s).运用晶体塑性有限元方法,使用ABAQUS 软件平台进行模拟分析,模拟结果如图3(b)所示.

图3 单开孔板单轴拉伸ABAQUS 模拟结果Fig.3 Simulation results for the plate with a single hole under uniaxial tensile load by ABAQUS
由模拟结果可以发现:①材料的强度极限随着孔径的增大而不断减小;②材料的延展性随着孔径的增大而不断减弱;③当孔径≤1 mm 时,材料的屈服应力相差不大,但当孔径为0.5∼1.0 mm 时延展性会被明显削弱,由原来的4%降低为3%;④随着孔径的增大(>1 mm),无论是材料的强度(包括屈服强度和极限强度)还是延展性,都有较大的下降.
图4 给出了孔径对材料极限强度影响的定量关系,横坐标为孔径与板宽的比值(D/H),纵坐标为约化极限强度,即开孔极限强度σD与未开孔极限强度σ0的比值.图中虚线为参考线,代表极限强度随孔径增大而线性下降,如孔径达到板宽H 的一半时,板的极限承载力降为一半;圆圈代表晶体塑性有限元计算结果;实线为采用二次多项式拟合计算数据得到的结果,相应表达式为
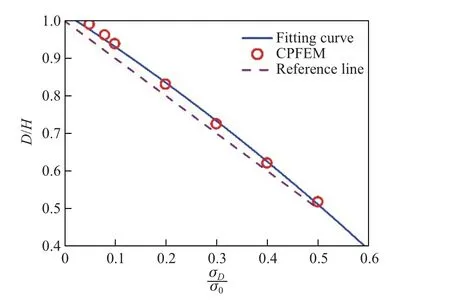
图4 孔径对板强度极限的影响Fig.4 Effect of void size on the ultimate strength of the plate
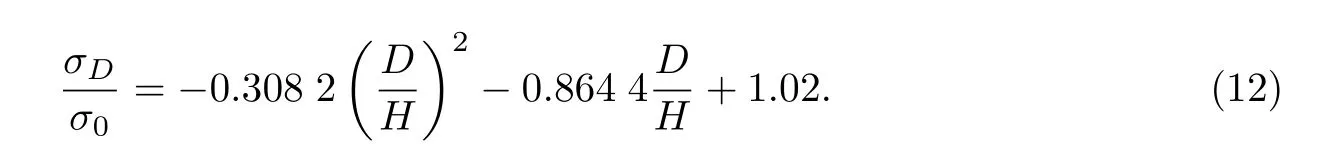
由图4 可知,在本工作计算范围内,开孔板的极限承载力比线性参考值要高,如当D/H=0.2 时,开孔板的极限承载力比线性参考值要高4.25%,但当孔径达到板宽一半时,该值降为2%,二者基本接近.因此,当孔径占比小于50%时,采用线性近似估算是偏于安全的;而超过50%时,由于应力集中的影响,开孔板的极限承载力将低于线性参考值,因工程中较为少见,此处未列出结果.另外,由图4 可见,采用二次多项式可以较好地模拟计算结果,拟合结果与计算数值的相关性为0.996.
3.2 双开孔孔间距对力学性能的影响
为研究双开孔的孔间距对于材料力学性能的影响,选取板材正中间位置的孔洞直径为1 mm,沿短边方向有另一个直径为1 mm 的孔洞.模拟不同孔间距情况下的材料拉伸试验结果如表2 所示.
从表2 可以看出,随着孔间距的减小,材料的强度极限有所下降,但下降的数值并不明显,如孔间距是孔径2 倍与3 倍相比,二者强度相差不足2%.因此,双开孔时只要保持两孔一定的距离(如孔径的2 倍),双孔的相互作用对于金属塑性材料强度极限的影响可忽略.

表2 不同孔间距下强度的比值Table 2 Ratio of strength at different hole spacings
3.3 双开孔相对位置对板材性能的影响
模型如图5(a)所示,选取直径为1 mm 的孔,将其置于板的中间位置,另一孔的位置可变,考虑到边界的影响,将两孔间的距离固定为2.5 mm.采用晶体塑性有限元方法分别计算5 种不同的双孔排布方式对板材性能的影响,结果如图5(b)所示.
由模拟结果可得:①双开孔排布方式对板材的延展性有重要影响,0◦排布时材料的强度和延展性最好,90◦排布时强度和延展性最差;②对于45◦排布方式,曲线在应变仅约为2.7%时呈现急速下降,这对工程安全是极为不利的.导致出现这一现象的主要原因是,一方面孔洞间存在应力集中现象,如图5(b)中的应力云纹插图所示,红色区域为应力较大的区域,两孔间应力明显较大;另一方面,从变形上看,对于45◦排布方式,两孔均发生了较为明显的变形,表明孔洞材料发生了剪切破坏,有大量位错滑移,从而导致颈缩现象更早发生.
图6 给出了上述5 种排布方式对板材名义极限强度的影响,纵坐标为约化强度σ/σ0.由图可以看出,①排布方式对开孔板的承载力有明显影响,整个曲线呈现出强烈的非线性特征.随着角度θ 的增大,板材承载力明显减小.当开孔沿板材轴线排布时,影响最小,σ/σ0=0.932 8比单孔情形下的σ/σ0=0.938 1 略小(见图4);当双孔沿轴线垂直方向排布时,影响最大,σ/σ0降低的幅度约为0.932 8 的两倍.②排布方式可分为3 个类型:当θ ≤30◦时,为影响较小的排布方式;当60◦≤θ ≤90◦时为影响较大的排布方式;而当30◦≤θ ≤60◦时为过渡区.由此可见,板材开孔时应尽量沿板材轴线分布.③采用反正切函数对模拟计算结果进行拟合,可得
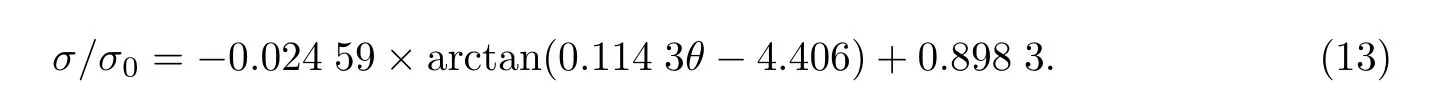
如此简洁的反正切函数形式可以很好地拟合计算数据,其相应的相关系数为0.997.
4 结论与讨论
本工作基于ABAQUS 二次开发平台VUMAT,实现了计及位错运动和孪晶效应的晶体塑性有限元理论程序的二次开发,并首次将这一方法应用于对多晶铜板材开孔问题的力学模拟研究中,主要结论如下.
(1) 对多晶铜模拟计算结果与试验结果以及传统有限元方法的结果吻合很好,验证了本工作二次开发的晶体塑性有限元程序具有良好的可靠性与实用性.与此同时,相较于传统有限元方法,CPFEM更能反映多晶材料的实际变形过程.
(2) 孔径对开孔板材的极限承载力有明显影响,呈现非线性特征,当孔径小于板宽一半时,以线性参考值作为设计标准是偏于安全的;而超过一半时,则不能以线性参考值作为设计标准值;二次多项式可以很好地模拟孔径与承载力间的非线性.
(3) 在孔距较小的情况下,孔径排布方式对开孔板材的极限承载力具有重要影响,且呈显著的非线性特征.排布方式可分为3 类,分别为弱影响区、强影响区和过渡区.对于承受单向拉伸荷载的板材,开孔时应选择沿轴线排布的方式.通过数值拟合发现,反正切函数可以很好地拟合孔径排布方式对开孔板材极限承载力的影响.
需要指出的是,实际板材失效与外部荷载有很大关联,上述分析的结论仅适用于板材沿轴向单向拉伸的情形,对于其他方式的荷载或复杂荷载,可以采用类似方法进行分析.因此,本工作一方面可为板材开孔提供有益的指导,同时也可为采用晶体塑性有限元方法研究缺陷孔洞对材料性能的影响提供理论依据.
