基于类属特征的多标签流形学习分类方法

亢浏越,黄 睿,孙广玲

(上海大学通信与信息工程学院,上海 200444)

在传统的机器学习框架中,一个对象只与单一类别的标签相关联[1].然而,在实际应用中,对象往往不是具有唯一语义的.例如,一篇新闻报道可以同时属于“经济”和“体育”类,一幅图像可以同时标注为“大海”和“天空”等.此时,传统的机器学习框架难以取得较好的分类效果.为了更好地描述数据对象,需要给每个对象赋予多个合适的类别标签,多标签学习也由此产生.目前,多标签学习已被广泛应用于文本分类[2-3]、图像标注[4-5]、音乐情感分类[6-7]等领域.

随着多标签学习研究的不断深入,涌现出大量多标签分类算法.这些算法大致可分为问题转换和算法改造两大类.问题转换是将多标签分类转换成多个单标签分类,再利用已有的单标签分类方法进行处理.代表性算法有二元关联(binary relevance,BR)法[4]、分类器链(classifier chain,CC)算法[8]、RAkEL(RAndom k-LabELsets)算法[9]等.算法改造是指通过改造单标签学习算法,使其能够直接用于多标签学习问题.代表性算法有多标签k 近邻(multi-label k-nearest neighbor,ML-kNN)算法[10]、排序支持向量机(ranking support vector machine,Rank-SVM)算法[11]、反向传播多标签学习(back-propagation multi-label learning,BP-MLL)法[12]等.

多标签流形学习(multi-label manifold learning,ML2)[13]是一种特殊的算法改造方法,先利用局部线性嵌入(local linear embedding,LLE)流形学习思想对类别标签的重要性进行量化,将逻辑型类别标签映射为数值型类别标签,再采用多输出支持向量回归进行分类.数值型标签可以指示同一样本不同标签的重要性程度,还能指示同一标签对不同样本的重要性程度.因此,数值型标签相比于逻辑标签携带了更多的语义信息,能更好地展现标签相关性.基于特征引导的标签信息富化(multi-label learning with feature-induced labeling information enrichment,MLFE)方法[14]思路与ML2类似,但是借助L1 正则化和交替方向乘子算法(alternating direction method of multiplier,ADMM)将逻辑型标签转换为数值型标签.Liu等[15-16]利用矩阵完备化(matrix completion)思想进行多标签学习,并通过图Laplacian构建的数据局部流形对目标函数进行正则化,提出基于图Laplacian 的矩阵完备化(matrix completion with graph Laplacian,MCLA)方法以及基于ADMM 优化的图Laplacian 矩阵完备化方法(LA-ADMM).Zhu 等[17]利用图Laplacian 构建标签的全局和局部流形,提出基于全局和局部标签相关性的多标签学习(multi-label learning with global and local label correlation,GLOCAL)方法.此外,流形学习也被用于多标签特征选择.文献[18]提出利用特征流形学习和稀疏正则化的多标签特征选择方法,通过流形和L21 范数正则化获得特征重要度系数矩阵.文献[19]提出一种基于流形学习的约束Laplacian 分值多标签特征选择方法,首先借鉴ML2方法将逻辑型标签转换成数值型标签,再利用数值标签之间的相关性对Laplacian 分值表达式进行修正.但是,这些多标签分类和特征选择方法没有考虑不同特征对不同类别标签的鉴别能力.事实上,不同类别标签往往具有独特的属性特征,这些特征与该标签关联性最强、最具有判别能力,被称为类属特征(label-specific features).与一般特征选择方法相比,类属特征构成的子集是随着类别的不同而变化的.文献[20]提出类属特征多标签学习(multi-label learning with label specific features,LIFT)方法,利用类属特征来表示样本并预测类别标签;通过在正负训练样本上分别进行聚类,利用聚类分析的结果获得每个标签的类属特征并进行分类.但这种方法只考虑了特征空间的转换,并没有考虑标签之间的关联性.文献[21]指出任何两个强关联的标签比弱关联的标签共享更多的类别属性,即所对应数据的特征相似度更大,并在此基础上提出一种学习类属特征(learning label specific features,LLSF)方法.

受上述研究的启发,本工作基于LLSF 和ML2,提出一种基于类属特征的多标签流形学习分类(label specific feature based multi-label manifold learning,LSF-ML2)方法.首先,计算样本的类别标签相关性,并用于优化类属特征重要度矩阵,确定不同类别标签的类属特征子集;再基于子集的特征流形构建标签流形,使标签从逻辑型变为数值型,从而更有效地体现标签关联性;最后,通过多输出支持向量回归实现分类.

1 LSF-ML2 算法

本工作所提算法LSF-ML2主要包括如下步骤:(1)计算特征重要度矩阵;(2)根据特征重要度矩阵对原始数据线性加权,获得新数据集;(3)基于流形学习思想将逻辑型标签转换为数值型标签,并采用多输出回归模型进行分类.

给定训练数据集为XL=[x1,x2,···,xn]T∈Rn×d,相应的逻辑型类别标签集为YL=[y1,y2,···,yn]T∈Rn×q.样本xi∈Rd对应的逻辑标签为yi∈{+1,−1}q,+1 表示样本和标签相关,−1 表示样本和标签无关.

定义 V=[v1,v2,···,vq] ∈Rd×q为类属特征重要度矩阵,若第i 个特征是第j 个标签的类属特征,则vij为非零实数值;反之,vij=0.矩阵V 反映了数据中每个特征对不同标签的重要程度,同时也反映了不同标签之间的关联性.对于第i 个类别标签,相应的vi=[vi1,vi2,···,vid]T可通过线性回归模型求解,即

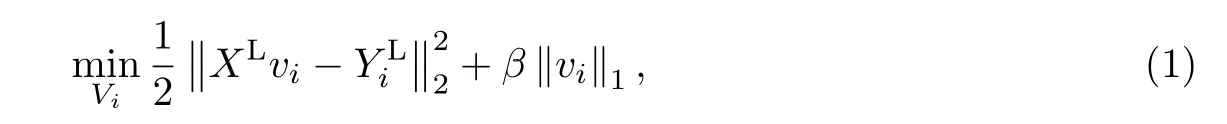
在多标签学习中,不同的类别标签之间往往存在一定的相关性.如果两类标签的关联性越强,所对应数据的类属特征相似度越大.相反,如果两类标签的关联性较弱,所对应数据的类属特征相似度也较小.标签的关联性由标签矢量的相关系数确定,对于标签yi与yj,有

式中:Cov(yi,yj)为yi与yj的协方差;D(yi)和D(yj)分别为yi,yj的方差.在引入成对标签相关性Cij后,式(1)进一步写为

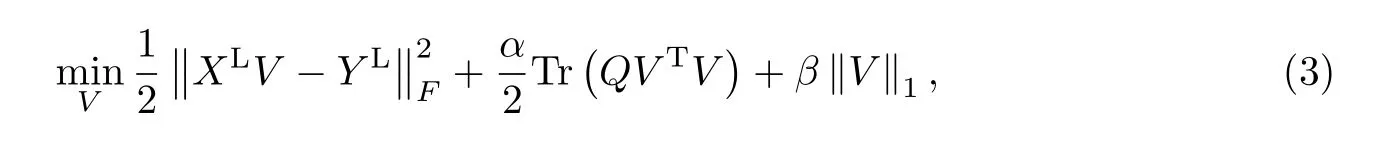
式中:Q ∈Rq×q,有Qij=1 −Cij;Tr(·)是矩阵的迹;∥·∥1和∥·∥F分别为1-范数和F-范数;权系数α,β ≥0.采用加速近端梯度(accelerated proximal gradient)方法求解.定义

具体步骤[15]如下.

(1) 初始化:令b0,b1←1,V0,V1←

(2) 迭代优化至收敛.

式中:t 为迭代次数;bt为线性聚合系数;Rt为基于第t 次和t −1 次迭代结果的聚合前向矩阵;∇f(Rt)为f(Rt)的梯度;Lf为利普希茨系数.由此,可获得矩阵V.在此基础上,确定新数据集S=[s1,s2,···,sn]T∈Rn×q为

式中:S是由类属特征对数据集XL的原特征线性加权产生的新数据集.

由于逻辑型标签无法反映数据不同类别标签间的重要度差异,因此通过流形学习,将逻辑标签转化为实数值,体现不同类别标签的相对重要性[13].根据平滑性假设,当两个样本相距很近时,其类别标签相似,即相邻的点很可能属于同一类别;相反,当两个样本相距较远时,其类别标签不同的可能性较大.也就是说,当两个样本相邻时,它们所属的类别矢量在标签空间的距离较近;当两个样本相距较远时,它们所属的类别矢量在标签空间的距离也较远.ML2利用LLE 思想,将特征空间的局部拓扑结构映射到类别标签的数值空间.借鉴该方法可获取类属特征子集的流形结构,若数据在局部范围内具有线性关系,样本si可以表示为其邻域样本点的线性组合.令表示点间的连接权重,可通过最小化下式获得该权重矩阵,

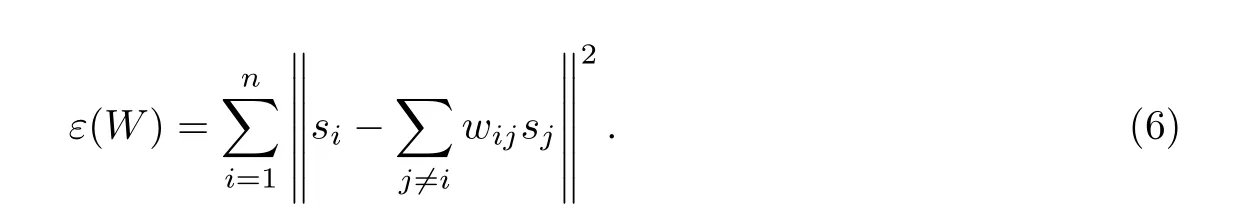
若sj不是si的K 近邻中的点,有wij=0.式(6)求解可转化为标准最小二乘规划问题.W 确定后,可在类别标签空间中建立局部区域内的线性关系.由于W 不变,使得类属特征空间的样本拓扑关系在类别标签的数值空间中得以保持.类别标签的流形结构可表示为

式中:µi∈Rq为yi对应的数值标签.同时添加如下约束使得数值标签能通过符号表征其是否与样本关联,

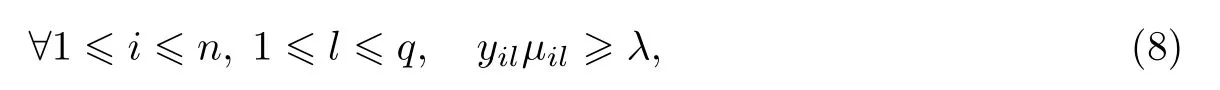
式中:λ >0.在给定W 和式(8)约束的前提下对式(7)进行最小化,可通过有约束的二次规划方法完成,获得实值标签.

最后,采用多输出回归的方法实现多标签分类.表1 对LSF-ML2进行了总结.

表1 LSF-ML2 算法Table 1 LSF-ML2 algorithm

2 实 验

2.1 数据集

为验证本工作所提算法的性能,分别在多标签数据集medical,corel5k,flags,20NG 上进行实验,表2 给出了所用数据集的统计信息描述.

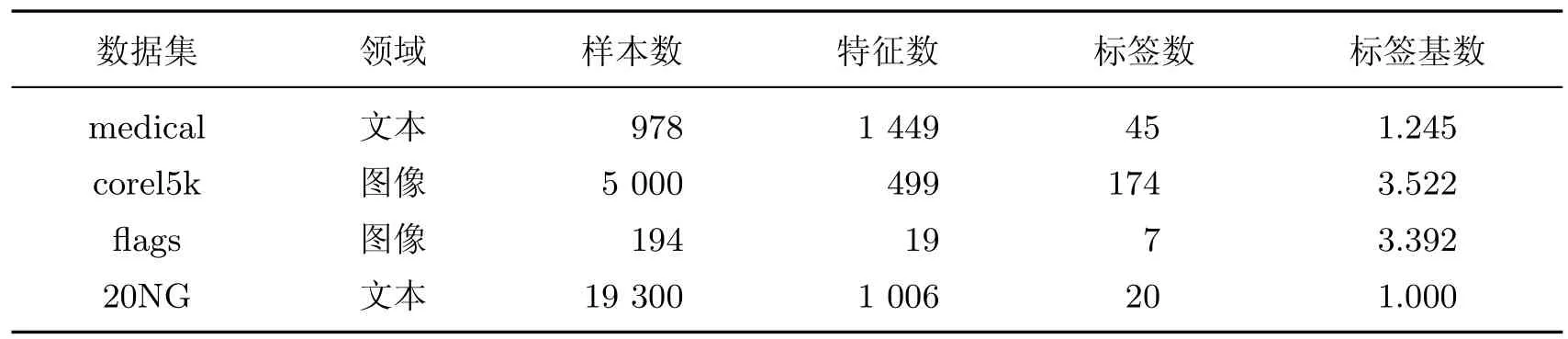
表2 实验所用数据集Table 2 Experimental data sets

2.2 评价指标

实验采用微平均(Micro F1)、基于样本的F1-measure、基于样本的准确度、基于标签的F1-measure、基于标签的准确度这5 个性能评价指标[8,21-23].上述评价指标分别从样本和标签的角度衡量算法性能.各评价指标的定义如下.

(1) 微平均(Micro F1):从单标签分类评价指标扩展而来,将每个标签元素都当成一个独立的元素,不考虑标签之间的区别,该值越大表示分类性能越好.定义

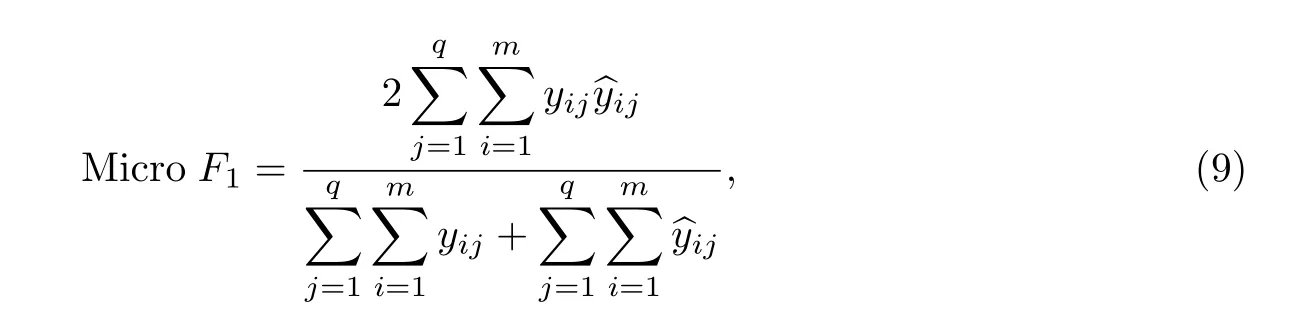
式中:yij和分别是第i 个样本的第j 个标签的真实值和预测值.

(2) 基于样本的F1-measure:对每个样本的精确度(precision)和召回率(recall)的调和平均,常用来评价多标签分类结果的好坏,该值越大表示分类效果越好.

(3)基于样本的准确度:以样本为基础,估计正确预测的标签占预测标签与真实标签集合的比例,该值越大表示分类效果越好.

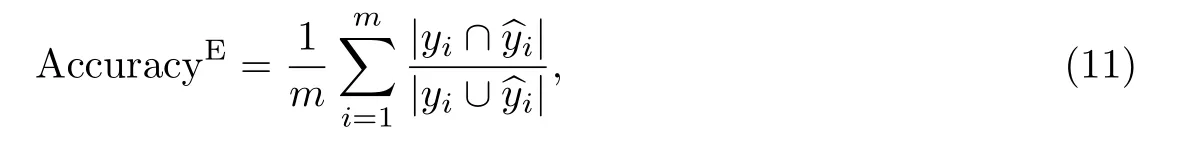
式中:yi和分别代表第i 个样本的真实标签矢量和预测标签矢量.

(4)基于标签的F1-measure:对每个标签的精确度和召回率的调和平均,该值越大表示分类效果越好.

(5)基于标签的准确度:以每个类别标签为基础,估计正确预测的标签占预测标签与真实标签集合的比例,该值越大表示分类效果越好.

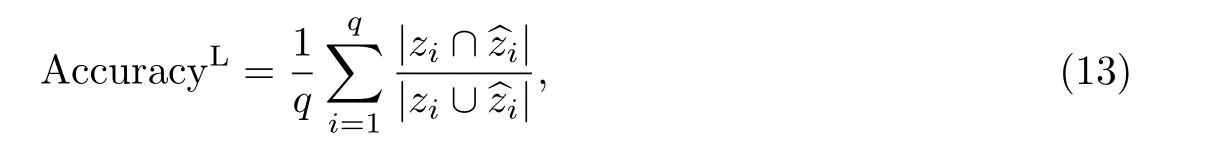
式中:zi和分别代表第i 个标签的真实标签矢量和预测标签矢量.

2.3 实验结果分析

为了验证本工作所提算法的有效性,将所提算法LSF-ML2与LLSF[21],ML2[13],MLkNN[10],MLFE[14]进行了比较,其中LLSF,ML2和MLFE 的参数设置与原文献相同.LLSF中α,β 和γ 的值分别设为0.1,0.1 和0.01,迭代100 次;ML2中λ,c1和c2分别设为1,1 和10;MLFE 中λ,c1和c2分别设为1,1 和2.c1和c2为多输出支持向量回归的惩罚因子.本工作所提算法LSF-ML2中的α,β,γ 以及迭代次数与LLSF 设置相同,λ,c1,c2与ML2设置相同,K 设为类别数加1.ML-kNN 的近邻设置为8.实验采用5 倍交叉验证,即将数据集随机分成5 等份,运行5 次,每次以其中1 份作为测试集,剩下4 份作为训练集.将5 次运行的测试集性能指标进行平均,作为最终评价结果.

表3 给出了不同算法的性能指标,表中实验结果均采用均值±方差(mean±std)的形式表示,并将性能最好的结果用黑体标出.为衡量算法在N1个数据集N2个指标上的性能,定义算法在第j 个指标下的平均排序值为

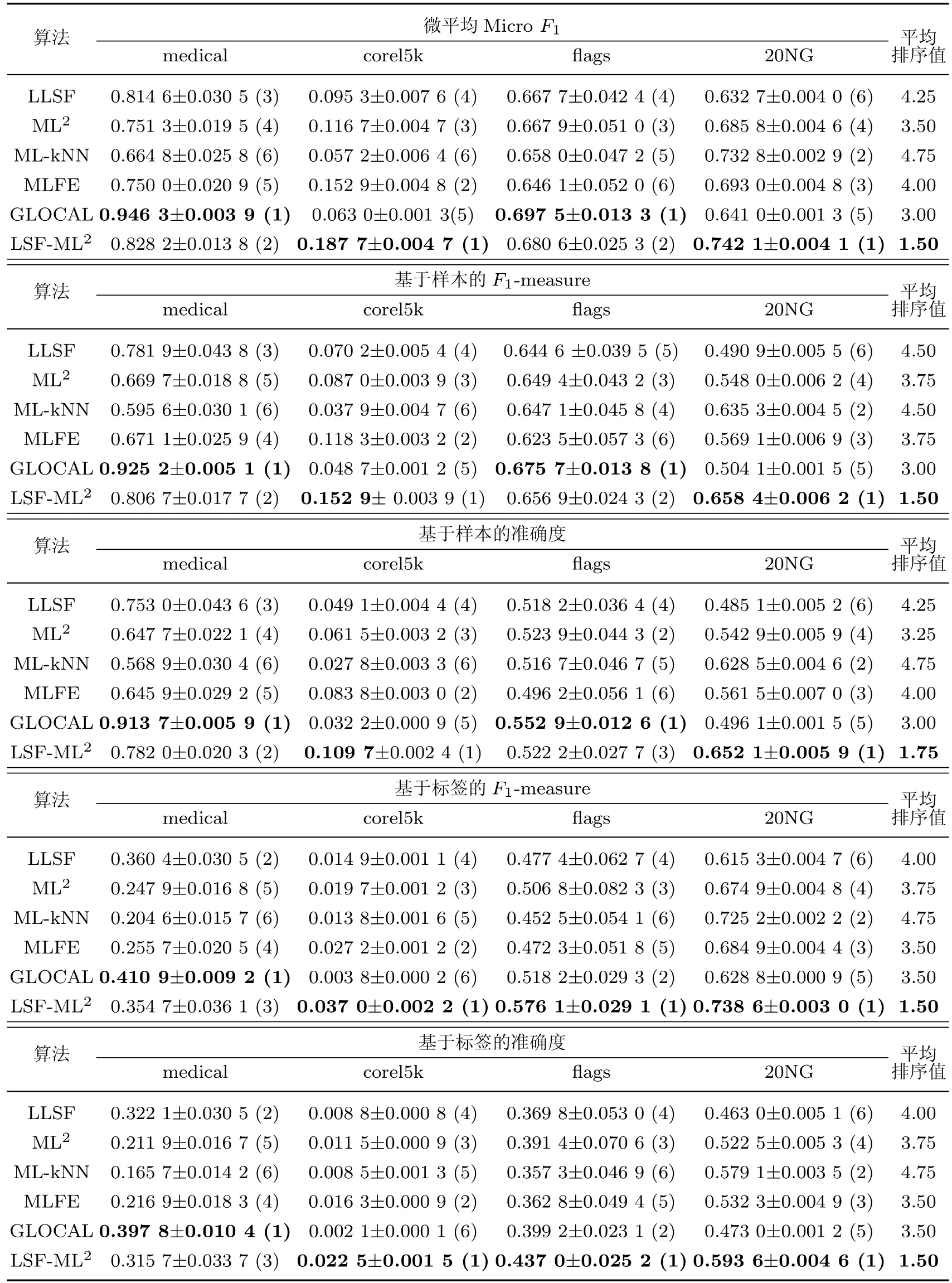
表3 不同分类算法的性能比较(mean±std)Table 3 Performance comparison of different classification methods (mean±std)

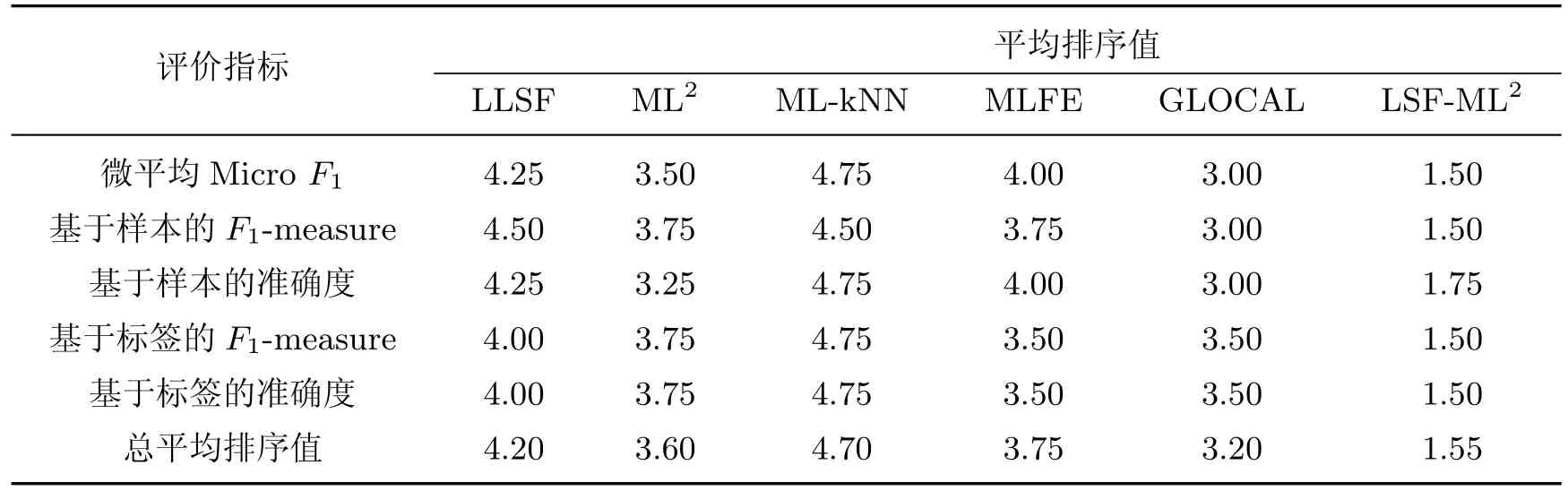
表4 不同分类算法在所有数据集上的平均排序值Table 4 Average rankings of different classification on all data sets

可以看到,3 个基于流形学习的算法ML2,GLOCAL 和LSF-ML2在总体性能上具有优势,其中GLOCAL 在数据集medical 的5 个指标和flags 的3 个指标上性能突出;但在数据集corel5k 和20NG 上性能基本处于末位,表现不佳.本工作所提算法LSF-ML2基于类属特征进行流形学习,在全部数据集的实验中性能均较为稳定地居于前3.在其余算法中,MLFE 也将逻辑标签实值化并采用多输出支持向量回归进行分类,性能稍逊于ML2.LLSF 基于类属特征进行分类,在数据集medical 上性能较好,但总体上逊于MLFE.以上5 种算法都考虑了类别标签的相关性,因此性能均优于忽略此相关性的ML-kNN.

为评估算法效率,表5 给出了各分类算法在不同数据集上花费的运算时间.该时间为5 次运行的平均值.实验所用计算机配置为Intel Core i5-8250U,8 G 内存,3.4 G 主频.可以看出,随着数据规模的增长,各算法的运算时间都有相应增加.ML-kNN 和LLSF 速度较快,其次是GLOCAL.虽然GLOCAL 采用流形学习,但算法是针对标签构建流形空间,因此运算量低于需要计算特征空间流形结构的LSF-ML2和ML2.同时,由于LSF-ML2基于类属特征进行分类,因此相比ML2降低了运算量.但对于规模较大的数据集,LSF-ML2无法满足实时性.MLFE 虽然没有计算流形结构,但在标签实值化过程中涉及L1 正则化目标函数的优化,较为费时,特别是针对较大数据集时,所需时间急剧增加.

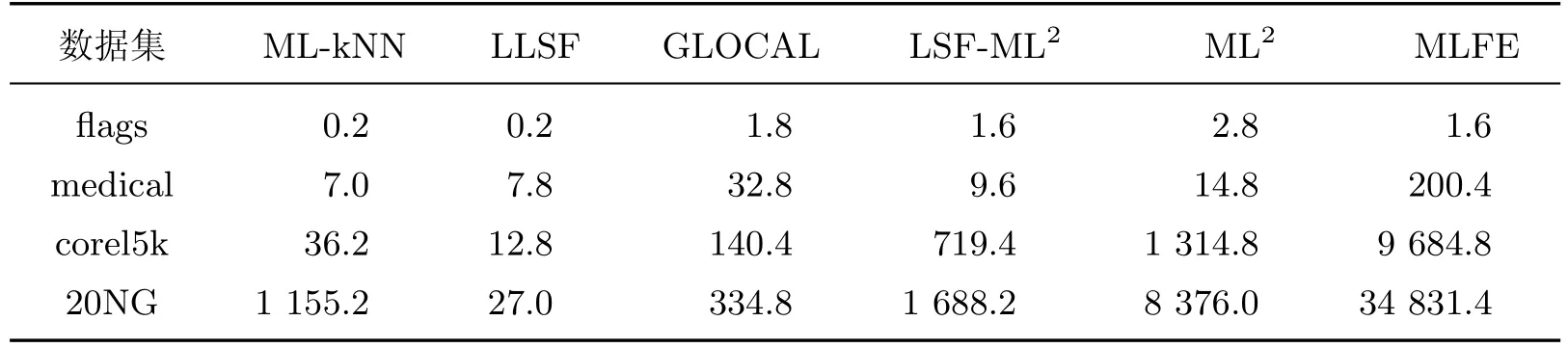
表5 不同分类算法的运算时间Table 5 Running time of different classification methods s

3 结束语

本工作提出一种基于类属特征的多标签流形学习分类方法LSF-ML2.基于类属特征的思想,从数据的特征全集中挑选出类属特征子集;基于类属特征子集的特征流形构建标签空间流形,将标签从逻辑型变为数值型,最后通过多输出支持向量回归实现分类.LSF-ML2利用标签相关性,将数据的类属特征空间和标签空间有机结合起来.多标签数据分类实验结果表明,LSF-ML2性能优于多种多标签分类方法.